当前位置： 首页 > news >正文

Keil5如何生成反汇编文件

news 2026/2/7 23:03:22

Keil5如何生成反汇编文件

  1. 在Keil5界面下点击选项，选择“User”，勾选“After Build/Rebuild”中“RUN #1”，复制fromelf --text -a -c --output=xxx.dis xxx.axf

在这里插入图片描述

  1. 在Linker栏中找到“Linker Control string”里最后-o后的.axf文件，将其复制下来替换第一步语句中的xxx.axf，然后点击OK

在这里插入图片描述

  1. 再次编译生成xxx.dis反汇编文件

在这里插入图片描述

在这里插入图片描述

相关文章：

Keil5如何生成反汇编文件

Keil5如何生成反汇编文件 在Keil5界面下点击选项，选择“User”，勾选“After Build/Rebuild”中“RUN #1”，复制fromelf --text -a -c --outputxxx.dis xxx.axf 在Linker栏中找到“Linker Control string”里最后-o后的.axf文件，将…...

编程日记 2024/1/15 1:35:58

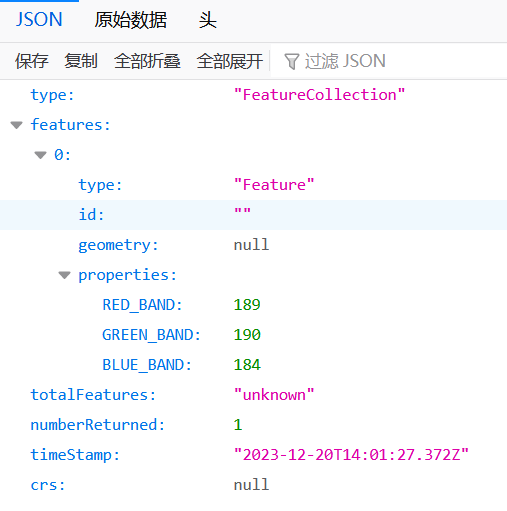
网络地图服务（WMS）详解

文章目录 1.概述2.GetCapabilities3.GetMap4.GetFeatureInfo 阅读本文之前可参考前文：《地图服务器GeoServer的安装与配置》与《GeoServer发布地图服务（WMS、WFS）》。 1.概述 经过前文的介绍，相信我们对WMS/WFS服务已经有了一个非…...

编程日记 2024/1/15 1:33:56

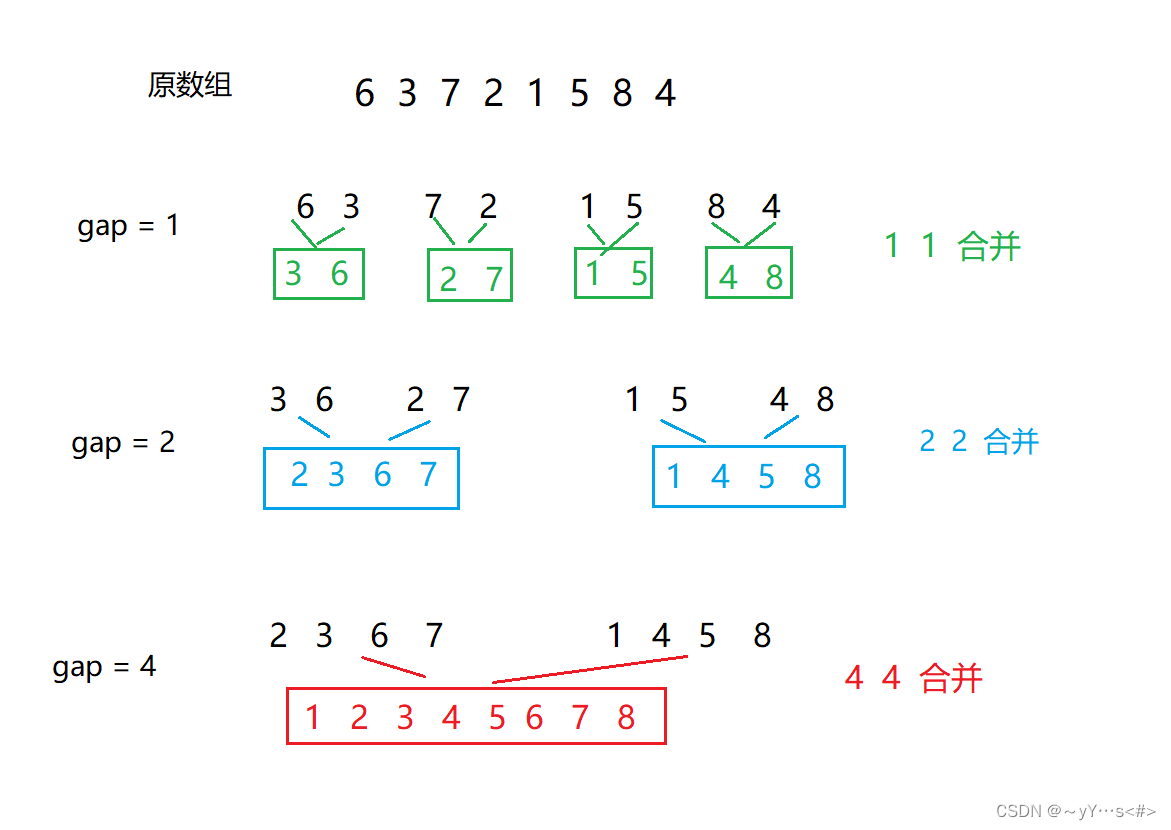
【排序篇3】快速排序、归并排序

目录 一、快速排序1.1 递归1.2 非递归 二、归并排序2.1 递归2.2 非递归 一、快速排序 1.1 递归 快速排序的递归采用二叉树的前序遍历的思路，单趟排序先确定好一个元素的位置，然后往后递归再确定其他子区域内的某个元素的位置，直到只有一个元…...

编程日记 2024/1/15 1:31:54

Python中的@property

在 Python 中，property 是一种装饰器，用于将一个方法转换成只读属性。通过使用 property 装饰器，你可以定义一个类的方法，使其在访问时可以像访问属性一样，而不是通过方法调用。 下面是一个简单的例子来说明 property …...

编程日记 2024/1/15 1:30:53

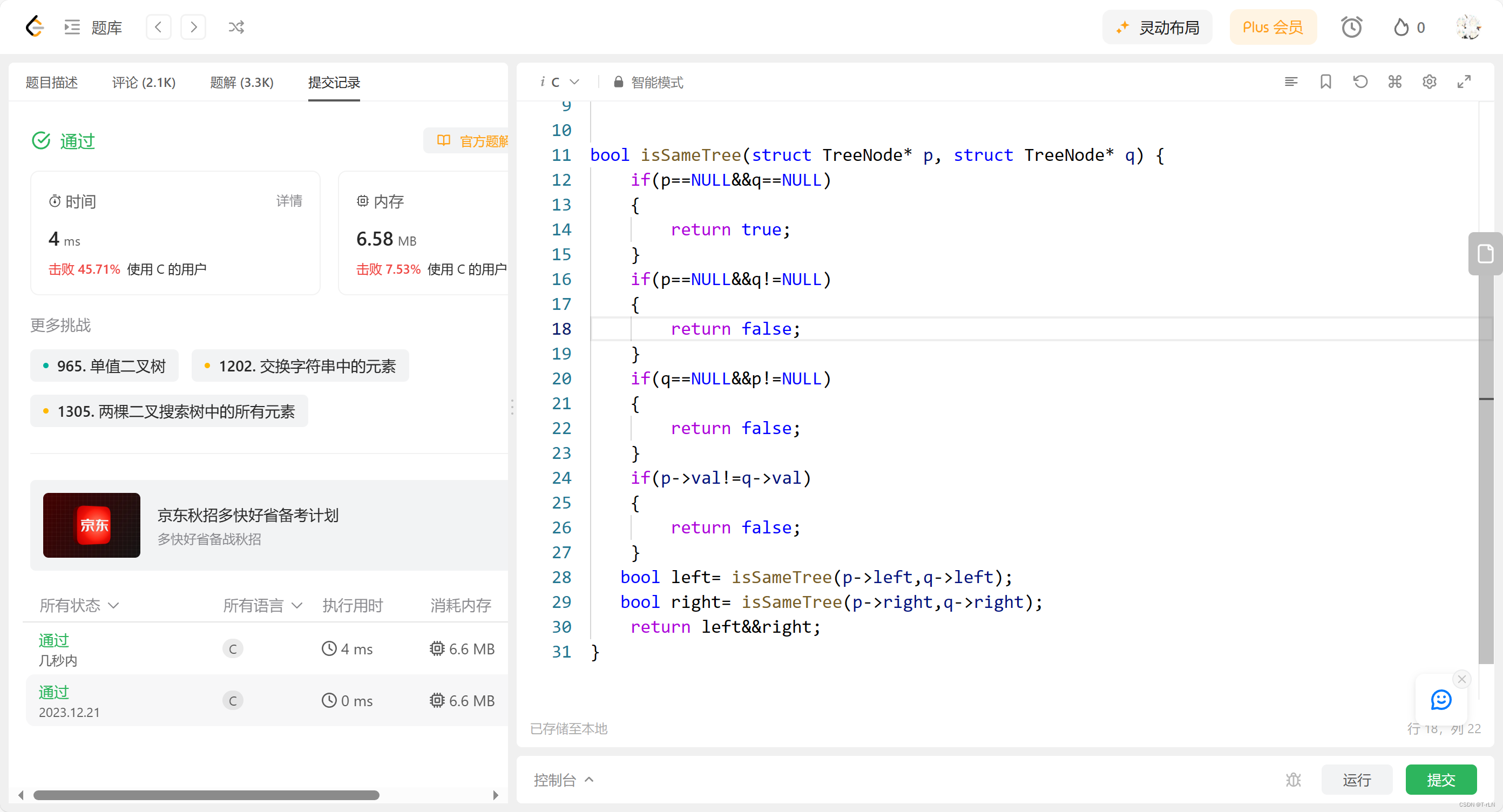
二叉树基础oj练习（单值二叉树、相同的树、二叉树的前序遍历）

讲了这么多数据结构相关的知识(可以看我的数据结构文章专栏): 抓紧刷题巩固一下了 目录 1.单值二叉树 题目描述 思路1 代码1 思路2 代码2 2.相同的树 题目描述 思路 代码 3.二叉树的前序遍历 代码 思路 1.单值二叉树 965. 单值二叉树 - 力扣（LeetCod…...

编程日记 2024/1/15 1:28:51

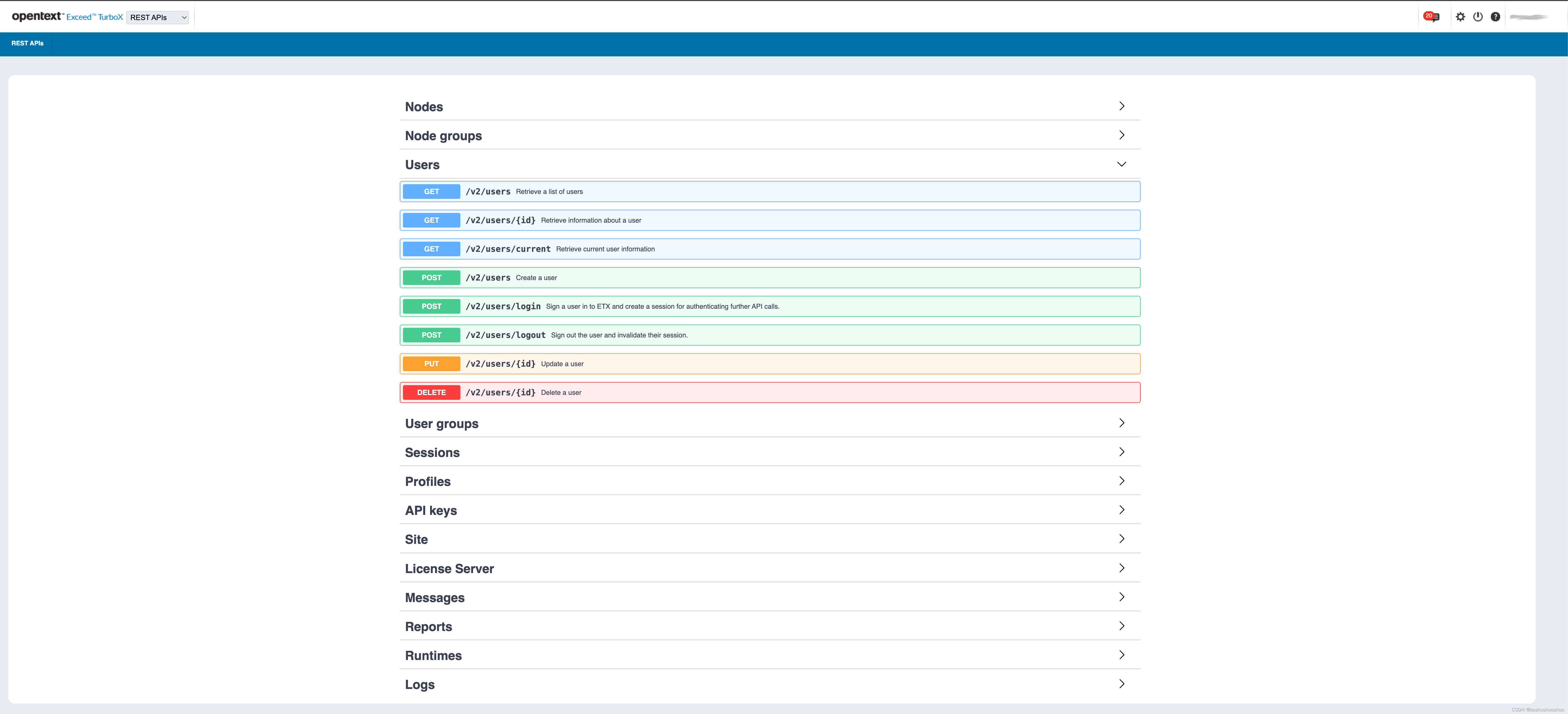
自动化创建ETX用户帐号

在芯片设计行业，ETX是常见的远程访问环境。用户在通过ETX访问远程环境前必须首先加入ETX系统，然后通过profile分配相关的环境的访问权限。 通常这些操作在ETX WEB页面手工操作，如果我们期望实现用户帐号注册全自动化，就需要将以上…...

编程日记 2024/1/15 1:26:49

Android 实现集合去重的方法

方法一&#xff1a;使用HashSet 将集合转换为HashSet。 Set<String> set new HashSet<>(list);将HashSet转换回List。 List<String> uniqueList new ArrayList<>(set);方法二&#xff1a;使用Java 8的Stream API 将列表转换为Stream。 Stream&l…...

编程日记 2024/1/15 1:25:48

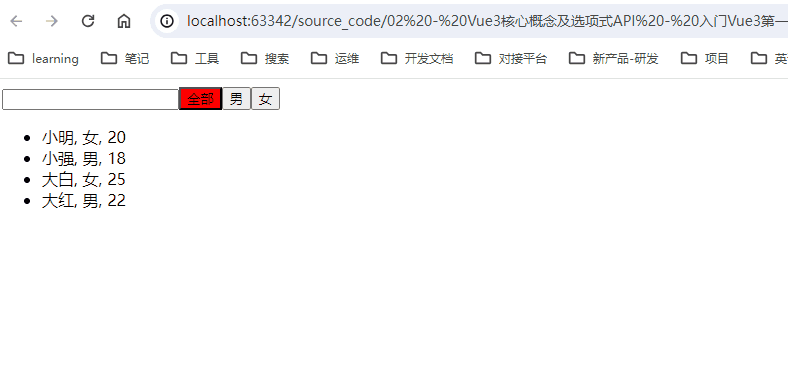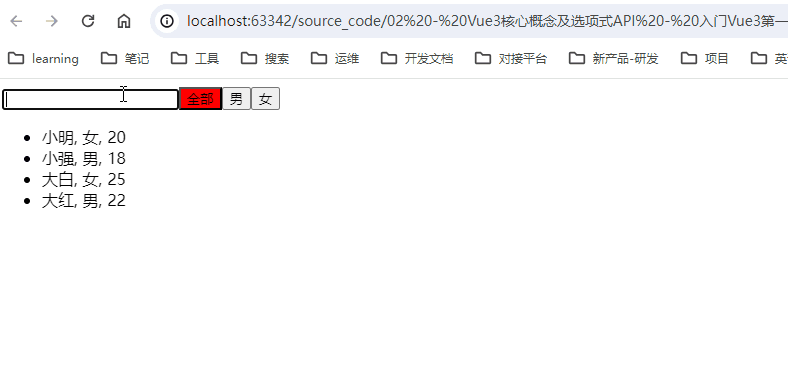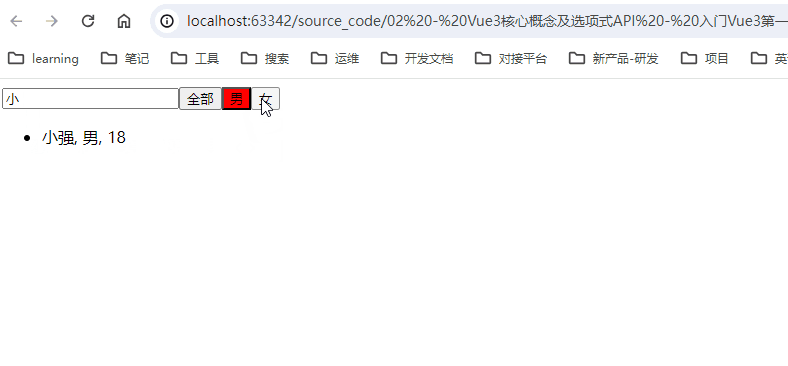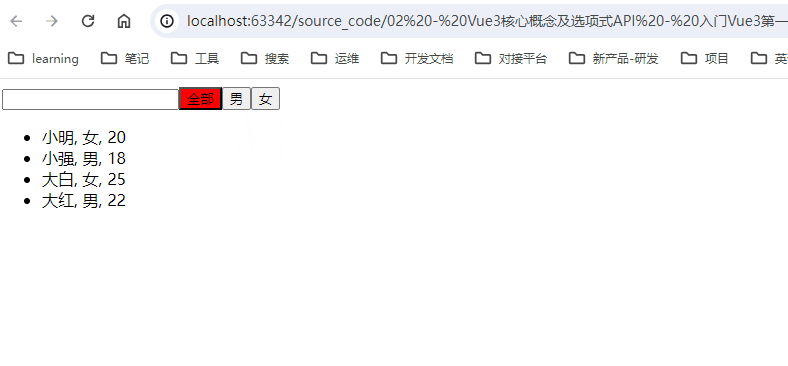
【Vue3】2-12 : 【案例】搜索关键词加筛选条件的综合

本书目录&#xff1a;点击进入 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 1.2、效果 1.3、json数据 - 02-data.json 1.4、代码 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 计算属性 - 绑定list&#xff0c;并过滤 input 双向绑定 - 当input改变时&…...

编程日记 2024/1/15 1:24:47

unity小程序websocket：nginx配置https (wss)转http (ws)及其他问题解决

目录 前言 实际运用场景 处理流程如下 nginx配置ssl和wss 配置过程中遇到的问题 1、无法连接服务器 2、通过IP可以访问&#xff0c;域名却不行 问题描述 解决 3、如何判断该域名是否备案了 前言 为了服务器网络的通用性&#xff0c;我们在实现移动端的游戏转微信小程序…...

编程日记 2024/1/15 1:22:45

MySql数据库对接Orcal数据库，需要考虑的前提问题

1.主表 从表的表关系&#xff1b;主键id 的关联问题&#xff1b; 2.字段类型的一致性问题&#xff08;备注&#xff1a;像varchar类型的一点要谨防数据过长抛错&#xff09;&#xff1b; 3.实体类字段两表一致性问题&#xff1b; 4.入表不为空问题&#xff0c;判空尽量在实体…...

编程日记 2024/1/15 1:21:45

K8S的存储卷---数据卷

容器内的目录和宿主机的目录进行挂载 容器在系统上的生命周期是短暂的。delete&#xff0c;K8S用控制器创建的pod&#xff0c;delete相当于重启&#xff0c;容器的状态也会恢复到初始状态。一旦回到初始状态&#xff0c;所有的后天编辑的文件都会消失 容器和节点之间创建一个…...

编程日记 2024/1/15 1:20:43

【量化交易故事】小明开启了量化创业之旅-01

故事开始于2023年的春天&#xff0c;小明是一位对金融市场充满热情的IT工程师。在经历了数次基于主观判断和个人情绪进行投资却收获平平后&#xff0c;他意识到传统交易方式中的人为因素难以避免&#xff0c;而这往往成为影响投资决策稳定性和准确性的关键障碍。在一次偶然的机…...

编程日记 2024/1/15 1:18:42

ffmpeg写YUV420文件碰到阶梯型横线或者条纹状画面的原因和解决办法

版权声明&#xff1a;本文为CSDN博主「文三~」的原创文章&#xff0c;遵循CC 4.0 BY-SA版权协议&#xff0c;转载请附上原文出处链接及本声明。 原文链接&#xff1a;https://blog.csdn.net/asdasfdgdhh/article/details/112831581 看到了&#xff0c;转载&#xff0c;留着备份…...

编程日记 2024/1/15 1:16:40

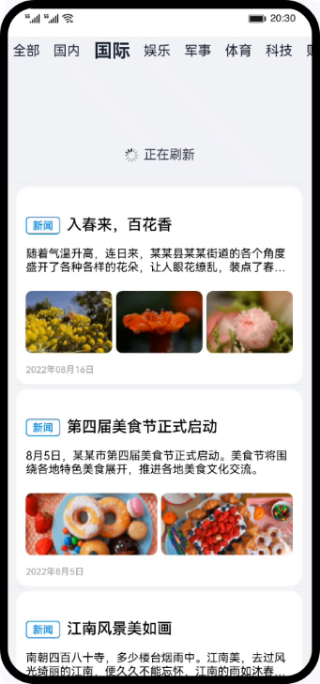
案例：新闻数据加载

文章目录 介绍相关概念相关权限约束与限制完整示例 代码结构解读构建主界面数据请求下拉刷新总结 介绍 本篇Codelab是基于ArkTS的声明式开发范式实现的样例&#xff0c;主要介绍了数据请求和touch事件的使用。包含以下功能&#xff1a; 数据请求。列表下拉刷新。列表上拉加载…...

编程日记 2024/1/15 1:15:39

数学的雨伞下：理解世界的乐趣

这本书没有一个公式&#xff0c;却讲透了数学的本质&#xff01; 《数学的雨伞下&#xff1a;理解世界的乐趣》。一本足以刷新观念的好书&#xff0c;从超市到对数再到相对论&#xff0c;娓娓道来。对于思维空间也给出了一个更容易理解的角度。 作者&#xff1a;米卡埃尔•洛奈…...

编程日记 2024/1/15 1:14:38

补充 vue3用户管理权限（路由控制）

之前有人问我 &#xff0c;如果是二级路由如何添加&#xff0c;这里我做一个补充吧。直接拿方法去用就行。也不做解释了。稍微看下就能看懂了 假设&#xff0c;后端返回给我们一个数据 [“/defa”,"/defa/defa1"] 这样的一个路由表&#xff0c;我们就需要通过这个路…...

编程日记 2024/1/15 1:09:34

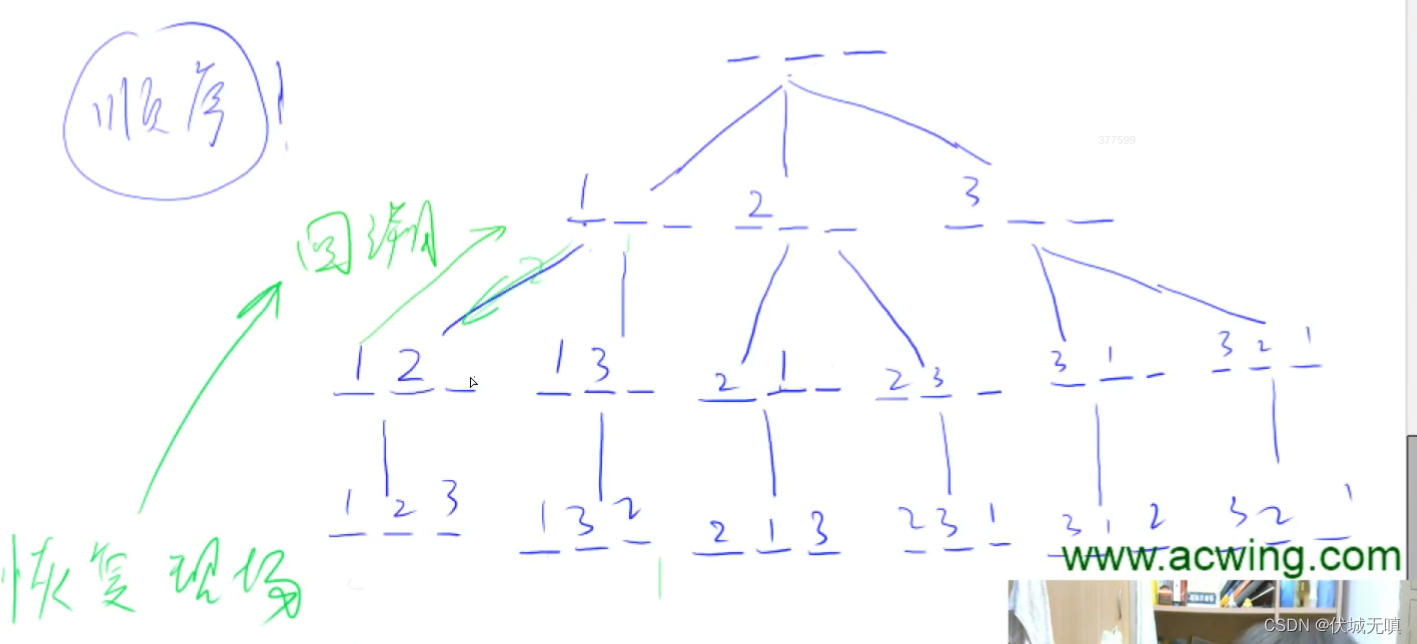
C++ 深度优先搜索DFS || 模版题：排列数字

给定一个整数 n &#xff0c;将数字 1∼n 排成一排&#xff0c;将会有很多种排列方法。 现在&#xff0c;请你按照字典序将所有的排列方法输出。 输入格式 共一行&#xff0c;包含一个整数 n 。 输出格式 按字典序输出所有排列方案&#xff0c;每个方案占一行。 数据范围 1…...

编程日记 2024/1/15 1:08:33

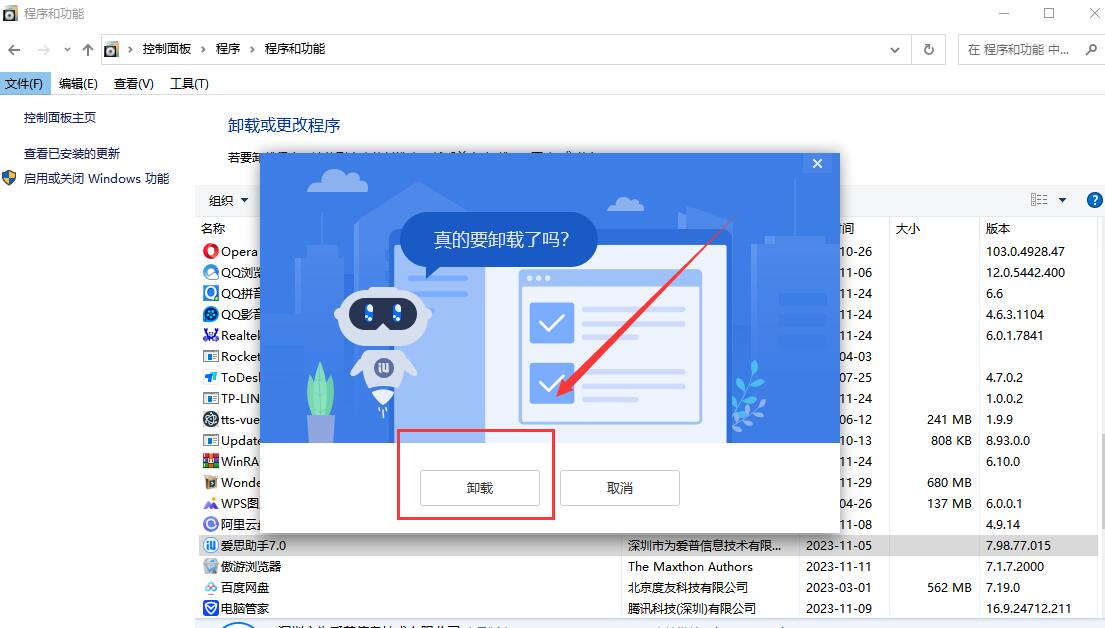
计算机找不到msvcp120.dll如何解决？总结五个可靠的教程

在计算机使用过程中&#xff0c;遇到“找不到msvcp120.dll”这一问题常常令人困扰。msvcp120.dll作为Windows系统中至关重要的动态链接库文件&#xff0c;对于许多应用程序的正常运行起着不可或缺的作用。那么&#xff0c;究竟是什么原因导致找不到msvcp120.dll呢&#xff1f;又…...

编程日记 2024/1/15 1:07:32

法线变换矩阵的推导

背景 在冯氏光照模型中&#xff0c;其中的漫反射项需要我们对法向量和光线做点乘计算。 从顶点着色器中读入的法向量数据处于模型空间&#xff0c;我们需要将法向量转换到世界空间&#xff0c;然后在世界空间中让法向量和光线做运算。这里便有一个问题&#xff0c;如何将法线…...

编程日记 2024/1/15 1:06:31

React.Children.map 和 js 的 map 有什么区别？

JavaScript 中的 map 不会对为 null 或者 undefined 的数据进行处理&#xff0c;而 React.Children.map 中的 map 可以处理 React.Children 为 null 或者 undefined 的情况。 React 空节点&#xff1a;可以由null、undefined、false、true创建 import React from reactexport …...

编程日记 2024/1/15 1:05:30

React 第五十五节 Router 中 useAsyncError的使用详解

前言 useAsyncError 是 React Router v6.4 引入的一个钩子&#xff0c;用于处理异步操作&#xff08;如数据加载&#xff09;中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误&#xff1a;捕获在 loader 或 action 中发生的异步错误替…...

编程新知 2025/11/25 10:36:53

三维GIS开发cesium智慧地铁教程（5）Cesium相机控制

一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点&#xff1a; 路径验证&#xff1a;确保相对路径.…...

编程新知 2025/12/1 19:23:04

大型活动交通拥堵治理的视觉算法应用

大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动&#xff08;如演唱会、马拉松赛事、高考中考等&#xff09;期间&#xff0c;城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例&#xff0c;暖城商圈曾因观众集中离场导致周边…...

编程新知 2026/1/23 7:15:40

【Go】3、Go语言进阶与依赖管理

前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课&#xff0c;做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程&#xff0c;它的核心机制是 Goroutine 协程、Channel 通道&#xff0c;并基于CSP&#xff08;Communicating Sequential Processes&#xff0…...

编程新知 2025/10/7 0:32:40

DBAPI如何优雅的获取单条数据

API如何优雅的获取单条数据 案例一 对于查询类API&#xff0c;查询的是单条数据&#xff0c;比如根据主键ID查询用户信息&#xff0c;sql如下&#xff1a; select id, name, age from user where id #{id}API默认返回的数据格式是多条的&#xff0c;如下&#xff1a; {&qu…...

编程新知 2026/2/2 22:06:13

Map相关知识

数据结构 二叉树 二叉树&#xff0c;顾名思义&#xff0c;每个节点最多有两个“叉”&#xff0c;也就是两个子节点&#xff0c;分别是左子 节点和右子节点。不过&#xff0c;二叉树并不要求每个节点都有两个子节点&#xff0c;有的节点只 有左子节点&#xff0c;有的节点只有…...

编程新知 2026/2/4 16:21:14

【生成模型】视频生成论文调研

工作清单 上游应用方向&#xff1a;控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

编程新知 2025/9/9 8:40:47

SiFli 52把Imagie图片，Font字体资源放在指定位置，编译成指定img.bin和font.bin的问题

分区配置 (ptab.json) img 属性介绍&#xff1a; img 属性指定分区存放的 image 名称&#xff0c;指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件&#xff0c;则以 proj_name:binary_name 格式指定文件名&#xff0c; proj_name 为工程 名&…...

编程新知 2026/1/23 10:51:19

Python 训练营打卡 Day 47

注意力热力图可视化 在day 46代码的基础上&#xff0c;对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

编程新知 2025/11/24 9:42:16

机器学习的数学基础：线性模型

线性模型 线性模型的基本形式为&#xff1a; f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法&#xff0c;得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

编程新知 2025/10/2 9:07:50