极简云源码已经开源
相关文章：
极简云源码已经开源
源码介绍 极简云已经开源 解绑卡密 查询卡密 总体来说还是很完善的 对接例子网盘里有 用户注册需要配置邮箱 上网页QQ邮箱标准版开启SMTP 然后生成授权码 后台发信邮箱里填就对了 实在不会配置邮箱的 可以下载网盘里的reg.php 把reg.php上传源码里的user目录 之后注册就不需要…...
Shell中cp和mv命令说明
在Shell（如Bash）中，cp 和 mv 是两个常用的命令，用于处理文件和目录。它们的用法和作用如下： cp 命令 作用：cp（copy的缩写）用于复制文件或目录。基本用法：cp [选项] 源文…...
cssip 第11章 : 安全网络架构和保护网络组件
11.1 OSI模型 协议：定义数据如何通过网络介质传输。 11.1.1 OSI模型的历史 开发 OSI 协议是为给所有计算机系统建立通用的通信结构或标准。 OSI模型表示：应用层、表示层、会话层、传输层、网络层、数据链路层、物理层。 11.1.3 封装/解…...
ITSS申报条件以及评审方式
01、四级申报基本条件： （1）具有独立法人地位； （2）已按照《运维服务能力成熟度》四级特征和关键指标建立了运维服务能力体系，且已有效运行三个月以上； （3）能…...
Qt中QByteArray之元素访问
访问QByteArray类对象中的某个元素主要有4种方式,分别为[]、at()、 data[]和constData[]。其中，[]和data]]方式为可读可写，at()和constData[]方式仅为可读。如果只是进行读操作，则通过at()和constData[]方式的访问速度最快，因为避…...
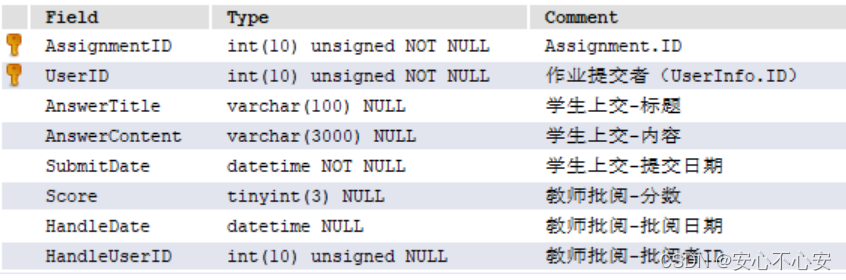
java实现教务管理系统
git地址：https://gitee.com/myshort-term/school-management 1.系统简介 开发教务管理系统程序，设计了ems（EMSApp）、dao（AssignmentDAO、CourseDAO、DeptDAO、ScoreDAO、UserDAO、EmailDAO）、domain&#…...
NPS配置https访问web管理页面
因为NPS默认也支持http的访问，所以在部署完后就一直没在意这个事情。 因为服务器是暴露在公网内的，所以还是要安全一点才行。不然一旦远控的机器被破解了就很危险了 一、使用nginx反向代理访问 1、首先在nps的配置文件里关闭使用https选项，…...
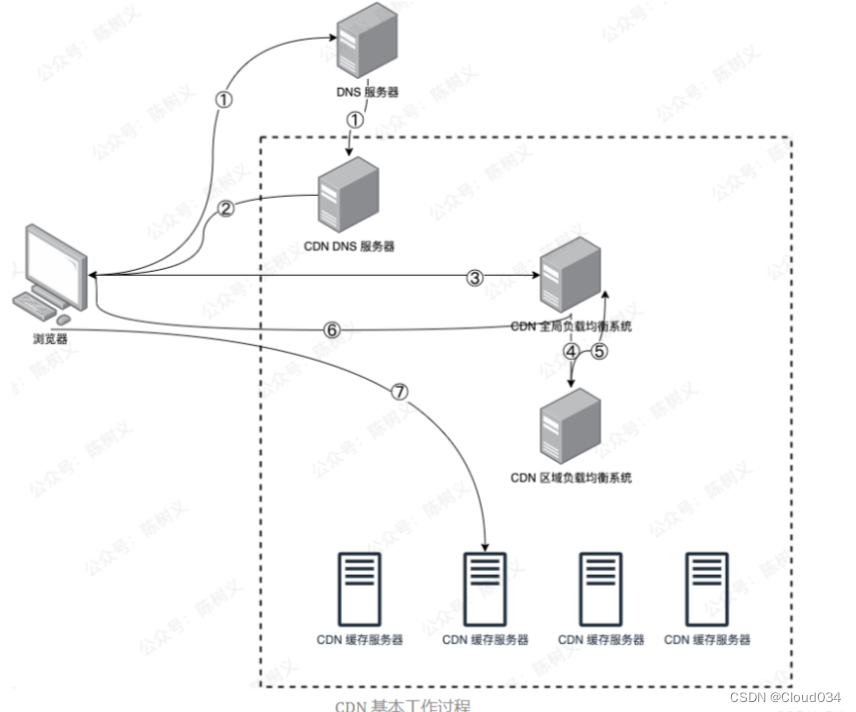
nginx和CDN应用
一、代理的工作机制 1．代替客户机向网站请求数据，从而可以隐藏用户的真实IP地址。 2．将获得的网页数据（静态 Web 元素）保存到缓存中并发送给客户机，以便下次请求相同的数据时快速响应。 二、代理服务器的…...
Keil5如何生成反汇编文件
Keil5如何生成反汇编文件 在Keil5界面下点击选项，选择“User”，勾选“After Build/Rebuild”中“RUN #1”，复制fromelf --text -a -c --outputxxx.dis xxx.axf 在Linker栏中找到“Linker Control string”里最后-o后的.axf文件，将…...
网络地图服务（WMS）详解
文章目录 1.概述2.GetCapabilities3.GetMap4.GetFeatureInfo 阅读本文之前可参考前文：《地图服务器GeoServer的安装与配置》与《GeoServer发布地图服务（WMS、WFS）》。 1.概述 经过前文的介绍，相信我们对WMS/WFS服务已经有了一个非…...
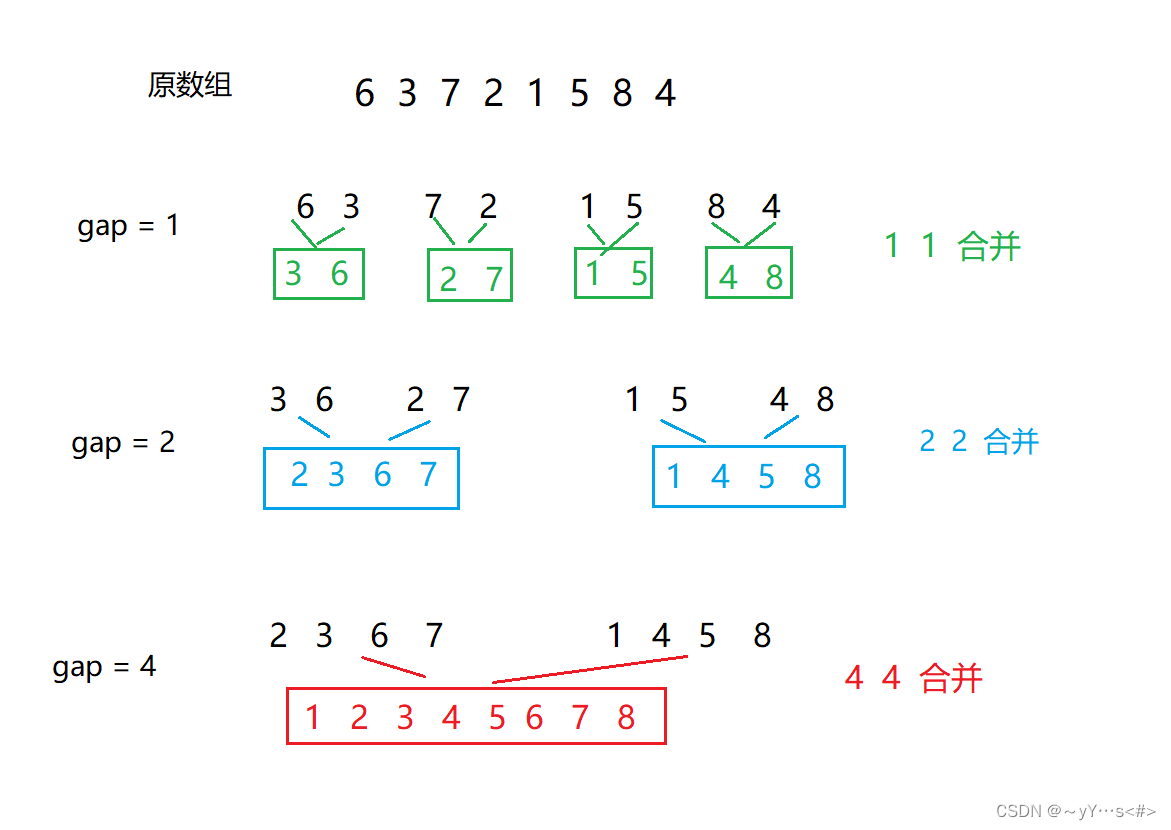
【排序篇3】快速排序、归并排序
目录 一、快速排序1.1 递归1.2 非递归 二、归并排序2.1 递归2.2 非递归 一、快速排序 1.1 递归 快速排序的递归采用二叉树的前序遍历的思路，单趟排序先确定好一个元素的位置，然后往后递归再确定其他子区域内的某个元素的位置，直到只有一个元…...
Python中的@property
在 Python 中，property 是一种装饰器，用于将一个方法转换成只读属性。通过使用 property 装饰器，你可以定义一个类的方法，使其在访问时可以像访问属性一样，而不是通过方法调用。 下面是一个简单的例子来说明 property …...
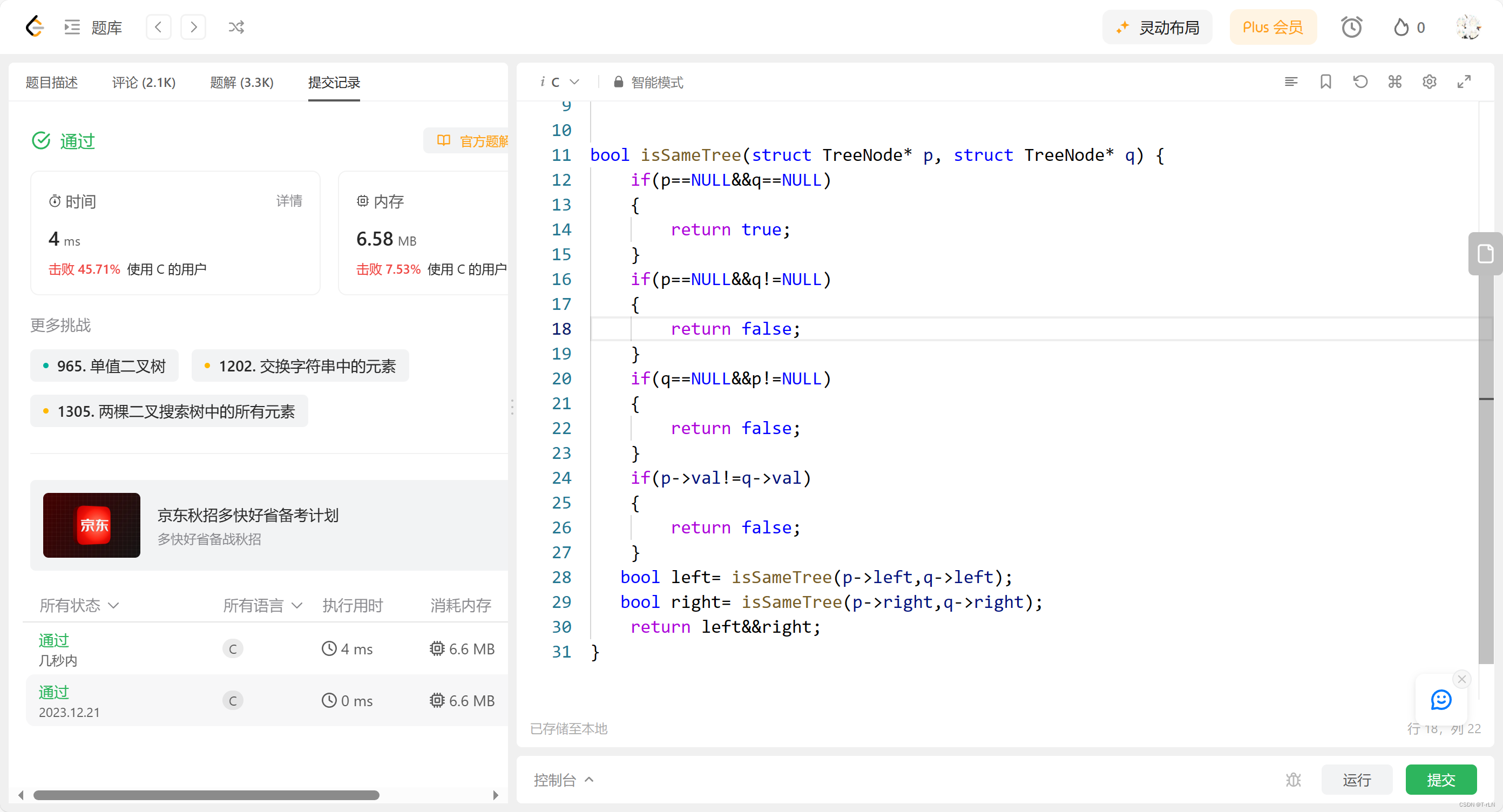
二叉树基础oj练习（单值二叉树、相同的树、二叉树的前序遍历）
讲了这么多数据结构相关的知识(可以看我的数据结构文章专栏): 抓紧刷题巩固一下了 目录 1.单值二叉树 题目描述 思路1 代码1 思路2 代码2 2.相同的树 题目描述 思路 代码 3.二叉树的前序遍历 代码 思路 1.单值二叉树 965. 单值二叉树 - 力扣（LeetCod…...
自动化创建ETX用户帐号
在芯片设计行业，ETX是常见的远程访问环境。用户在通过ETX访问远程环境前必须首先加入ETX系统，然后通过profile分配相关的环境的访问权限。 通常这些操作在ETX WEB页面手工操作，如果我们期望实现用户帐号注册全自动化，就需要将以上…...
Android 实现集合去重的方法
方法一：使用HashSet 将集合转换为HashSet。 Set<String> set new HashSet<>(list);将HashSet转换回List。 List<String> uniqueList new ArrayList<>(set);方法二：使用Java 8的Stream API 将列表转换为Stream。 Stream&l…...
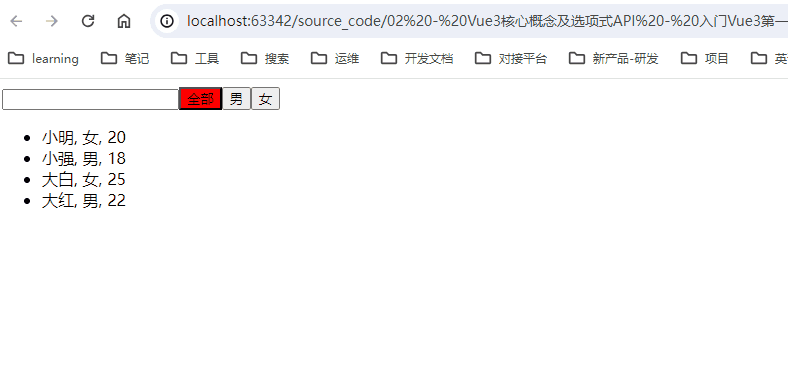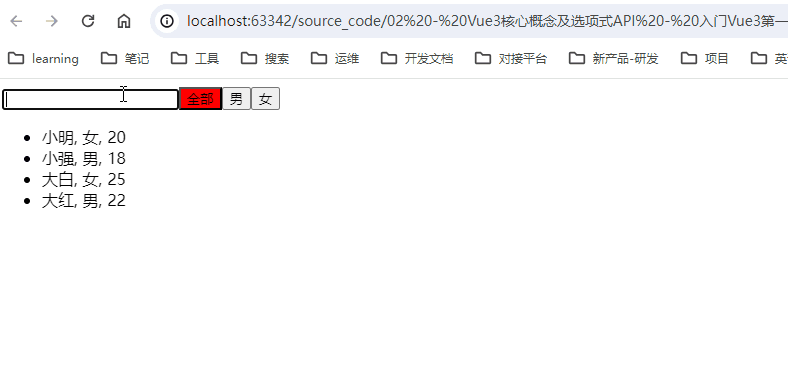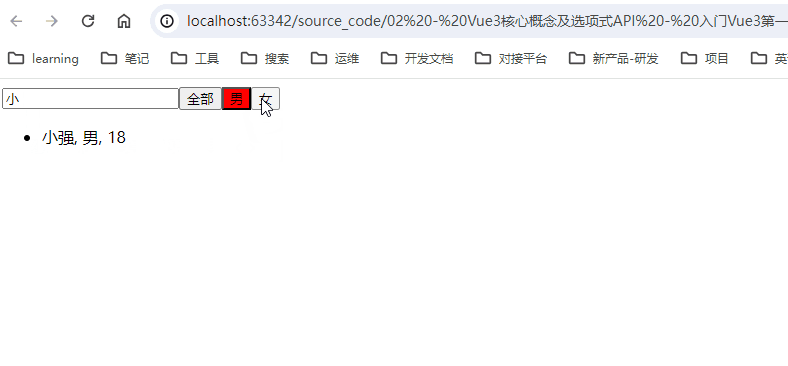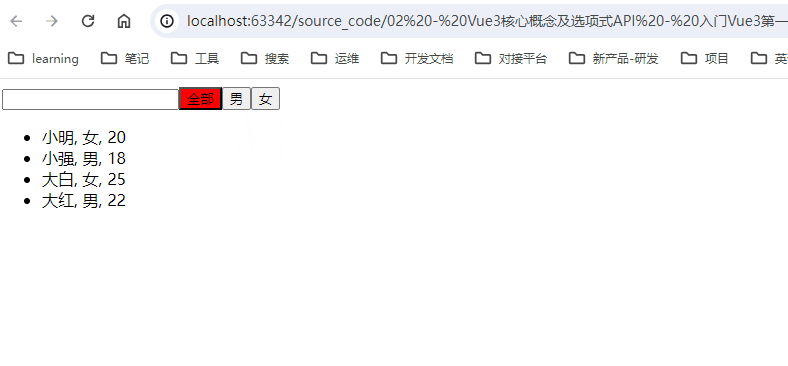
【Vue3】2-12 : 【案例】搜索关键词加筛选条件的综合
本书目录：点击进入 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 1.2、效果 1.3、json数据 - 02-data.json 1.4、代码 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 计算属性 - 绑定list，并过滤 input 双向绑定 - 当input改变时&…...
unity小程序websocket：nginx配置https (wss)转http (ws)及其他问题解决
目录 前言 实际运用场景 处理流程如下 nginx配置ssl和wss 配置过程中遇到的问题 1、无法连接服务器 2、通过IP可以访问，域名却不行 问题描述 解决 3、如何判断该域名是否备案了 前言 为了服务器网络的通用性，我们在实现移动端的游戏转微信小程序…...
MySql数据库对接Orcal数据库，需要考虑的前提问题
1.主表 从表的表关系；主键id 的关联问题； 2.字段类型的一致性问题（备注：像varchar类型的一点要谨防数据过长抛错）； 3.实体类字段两表一致性问题； 4.入表不为空问题，判空尽量在实体…...
K8S的存储卷---数据卷
容器内的目录和宿主机的目录进行挂载 容器在系统上的生命周期是短暂的。delete，K8S用控制器创建的pod，delete相当于重启，容器的状态也会恢复到初始状态。一旦回到初始状态，所有的后天编辑的文件都会消失 容器和节点之间创建一个…...
【量化交易故事】小明开启了量化创业之旅-01
故事开始于2023年的春天，小明是一位对金融市场充满热情的IT工程师。在经历了数次基于主观判断和个人情绪进行投资却收获平平后，他意识到传统交易方式中的人为因素难以避免，而这往往成为影响投资决策稳定性和准确性的关键障碍。在一次偶然的机…...
【Linux】shell脚本忽略错误继续执行
在 shell 脚本中，可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行，可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令，并忽略错误 rm somefile…...
YSYX学习记录（八）
C语言，练习0： 先创建一个文件夹，我用的是物理机： 安装build-essential 练习1： 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件，随机修改或删除一部分，之后…...
Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
学习STC51单片机31（芯片为STC89C52RCRC）OLED显示屏1
每日一言 生活的美好，总是藏在那些你咬牙坚持的日子里。 硬件：OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写，"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...
css的定位（position）详解：相对定位 绝对定位 固定定位
在 CSS 中，元素的定位通过 position 属性控制，共有 5 种定位模式：static（静态定位）、relative（相对定位）、absolute（绝对定位）、fixed（固定定位）和…...
Unsafe Fileupload篇补充-木马的详细教程与木马分享（中国蚁剑方式）
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马（服务器方面的）的原理，连接，以及各种木马及连接工具的分享 文件木马：https://w…...
接口自动化测试：HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具，支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议，涵盖接口测试、性能测试、数字体验监测等测试类型…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分，它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构： use strict;/…...
WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC？ WebRTC（Web Real-Time Communication）是一个支持网页浏览器进行实时语音…...
vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...