优先级队列(Priority Queue)
文章目录
- 优先级队列(Priority Queue)
- 实现方式
- 基于数组实现
- 基于堆实现
- 方法实现
- offer(E value)
- poll()
- peek()
- isEmpty()
- isFull()
- 优先级队列的实现细节
优先级队列(Priority Queue)
优先级队列是一种特殊的队列,其中的元素不是按照进入队列的顺序出队,而是按照元素的优先级出队。在优先级队列中,元素的优先级最高的将会首先出队。
实现方式
基于数组实现
以下是基于数组的优先级队列的简单实现:
public class PriorityQueueArray<E extends Priority> {private E[] array;private int size = 0;public PriorityQueueArray(int capacity) {array = (E[]) new Object[capacity];}public boolean offer(E value) {if (size >= array.length) return false;int i = size - 1;while (i >= 0 && array[i].priority < value.priority) {array[i + 1] = array[i];i--;}array[i + 1] = value;size++;return true;}public E poll() {if (size == 0) return null;E result = array[size - 1];array[size - 1] = null;size--;return result;}public E peek() {if (size == 0) return null;return array[size - 1];}public boolean isEmpty() {return size == 0;}public boolean isFull() {return size == array.length;}
}
这个实现中,offer方法将元素插入到正确的位置以保持数组的有序性,poll方法删除并返回优先级最高的元素,peek方法返回但不删除优先级最高的元素。isEmpty和isFull方法分别用于检查队列是否为空或已满。
基于堆实现
基于数组的实现有一些缺点。例如,插入和删除元素可能需要移动大量的元素,特别是在最坏的情况下,这可能需要移动整个数组。因此,这种实现的时间复杂度可能会达到O(n),其中n是队列的大小。
这就是为什么在实践中,我们通常会使用更复杂的数据结构,如堆,来实现优先级队列。使用堆实现的优先级队列可以在O(log n)的时间复杂度内插入和删除元素,这比基于数组的实现更有效率。
优先级队列通常使用堆(Heap)数据结构来实现。在Java中,可以通过实现Queue接口来创建一个优先级队列。下面的代码是一个使用最大堆实现的优先级队列:
public class PriorityQueue2<E extends Priority> implements Queue<E> {Priority[] array;public int size;public PriorityQueue2(int capacity) {array = new Priority[capacity];}...
}
这个优先级队列中的元素必须实现Priority接口,这个接口定义了元素的优先级。
方法实现
优先级队列通常包含以下方法:
offer(E value)
将元素插入到优先级队列中。如果队列已满,返回false;否则,将元素插入到正确的位置以保持堆的性质,并返回true。
@Override
public boolean offer(E value) {if(isFull())return false;if (size == 0){array[0] = value;}else{int child = size;int partent = (child - 1) / 2;while (child > 0 && value.priority > array[partent].priority){array[child] = array[partent];child = partent;partent = (child - 1) / 2;}array[child] = value;}size++;return true;
};
poll()
移除并返回优先级最高的元素。如果队列为空,返回null。
@Override
public E poll() {if (isEmpty())return null;E result = (E)array[0];array[0] = array[size-1];array[size] = null;size--;down(0);return result;
}private void down(int parent){int child1 = parent * 2 + 1;int child2 = parent * 2 + 2;if(child1 >= size )return;int maxIndex = child2 < size && array[child2].priority > array[child1].priority ? child2: child1;if(array[maxIndex].priority <= array[parent].priority)return;change(parent,maxIndex);down(maxIndex);
}private void change(int parent,int child){Priority p = array[parent];array[parent] = array[child];array[child] = p;
}
peek()
返回优先级最高的元素,但不移除它。如果队列为空,返回null。
@Override
public E peek() {if (isEmpty())return null;return (E)array[0];
}
isEmpty()
判断队列是否为空。
@Override
public boolean isEmpty() {return size == 0;
}
isFull()
判断队列是否已满。
@Override
public boolean isFull() {return size == array.length;
}
优先级队列的实现细节
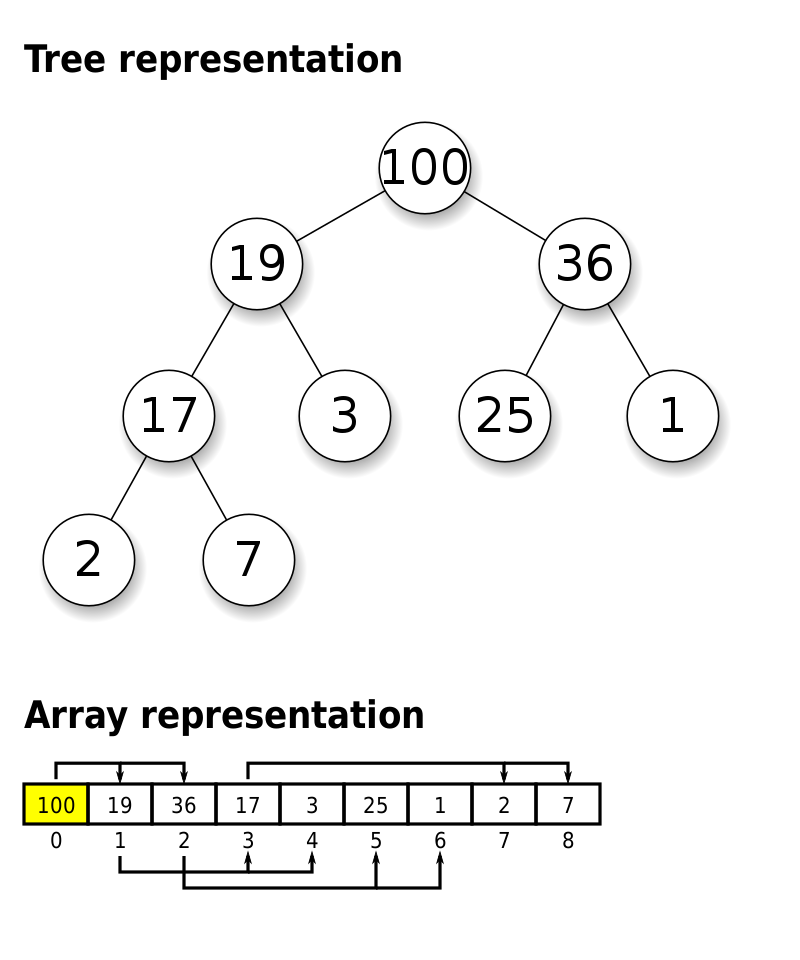
优先级队列的实现主要基于一个堆结构。堆是一种特殊的完全二叉树,其中每个节点的值都大于或等于其子节点的值(最大堆)或小于或等于其子节点的值(最小堆)。
在我们的实现中,我们使用了一个数组array来存储堆的元素,并使用size来记录堆的大小。这是因为完全二叉树可以非常方便地用数组来表示。具体来说,对于数组中的任何一个元素,其左子节点的索引是2 * index + 1,右子节点的索引是2 * index + 2,而其父节点的索引是(index - 1) / 2。
相关文章:

优先级队列(Priority Queue)
文章目录 优先级队列(Priority Queue)实现方式基于数组实现基于堆实现方法实现offer(E value)poll()peek()isEmpty()isFull() 优先级队列的实现细节 优先级队列(Priority Queue) 优先级队列是一种特殊的队列,其中的元素…...
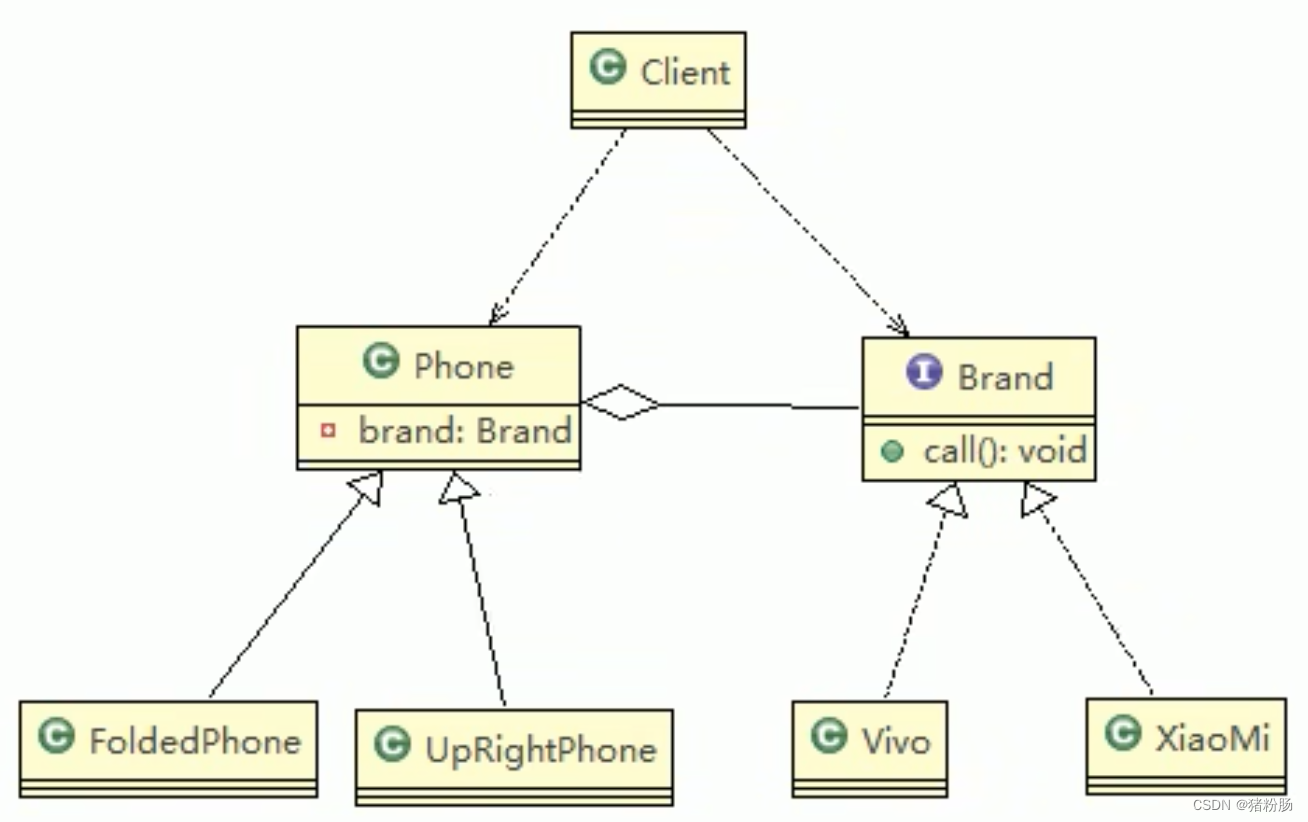
12-桥接模式(Bridge)
意图 将抽象部分与它的实现部分分离,使他们可以独立地变化 个人理解 一句话概括就是只要是在抽象类中聚合了某个接口或者抽象类,就是使用了桥接模式。 抽象类A中聚合了抽象类B(或者接口B),A的子类的方法中在相同的场…...

Zookeeper+Kafka概述
一 Zookeeper 1.1 Zookeeper定义 Zookeeper是一个开源的、分布式的,为分布式框架提供协调服务的Apache项目。 1.2 Zookeeper特点 Zookeeper:一个领导者(leader),多个跟随者(Follower)组成的…...
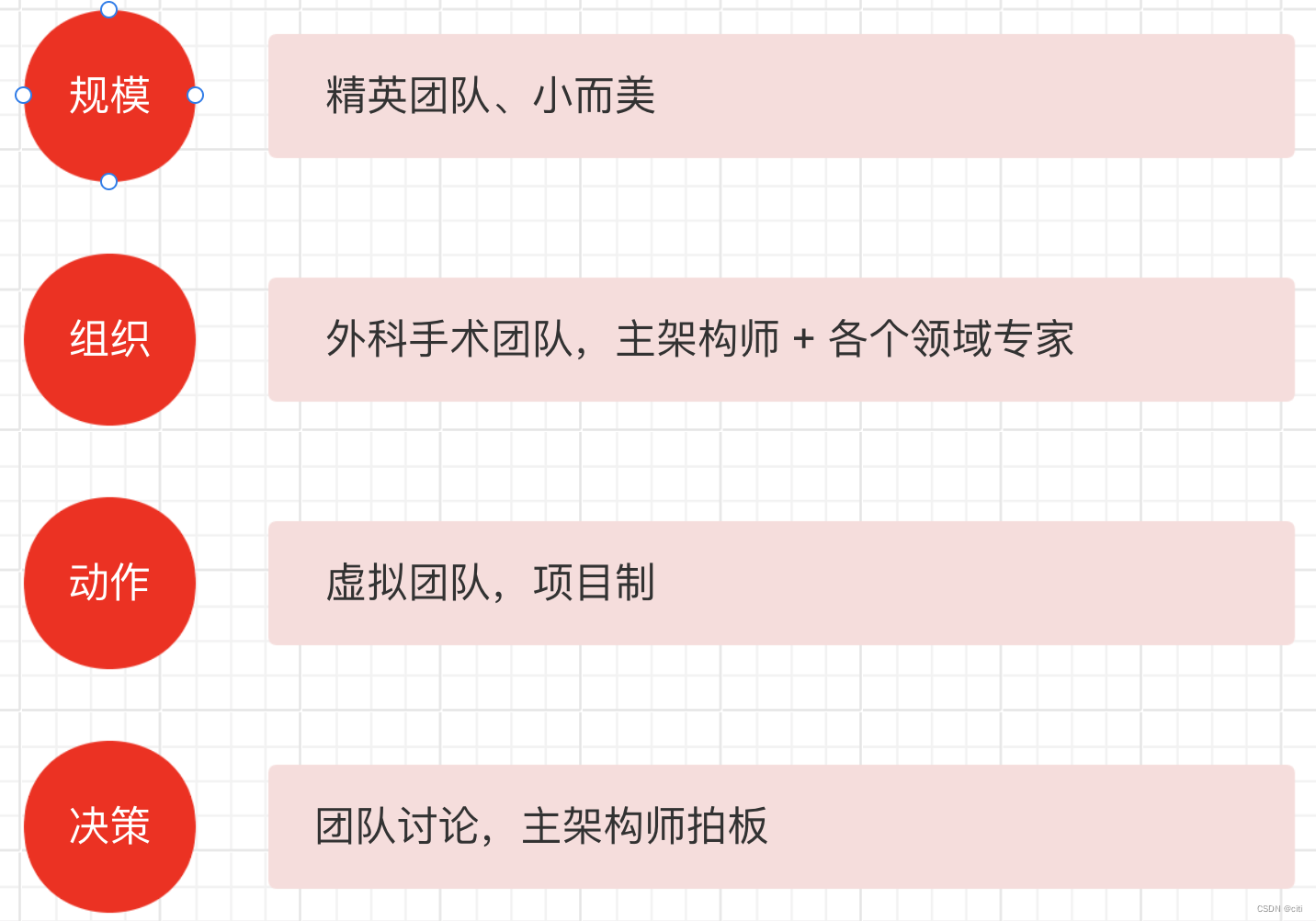
架构师 - 架构师是做什么的 - 学习总结
架构师核心定义 架构师是什么 架构师是业务和技术之间的桥梁 架构师的核心职责是消除不确定性、和降低复杂性 架构设计环 架构师的三个核心能力 架构师的三个关键思维 架构师主要职责 架构设计 Vs 方案设计 架构设计前期 主要任务 澄清不确定性 明确利益干系人的诉求消除冲…...
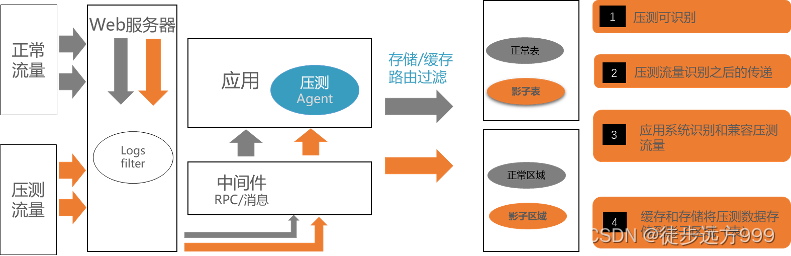
全链路压测方案(一)—方案调研
一、概述 在业务系统中,保证系统稳定至关重要,直接影响线上业务稳定和性能。测试工作作为保证生产质量的最后一关,扮演者重要的角色。全链路压测是一种重要的测试工具和手段。可以解决系统中多环节多节点无法全流程打满流量的痛点问题&a…...

c++关键字const
C中的const是一种常量修饰符。在变量、函数参数和成员函数中使用const可以限制其对数据的修改。 const修饰的数据在定义时必须进行初始化,且不能被修改,因此使用const可以提高代码的安全性和可读性。在C中,const修饰的成员函数表示该函数保证…...
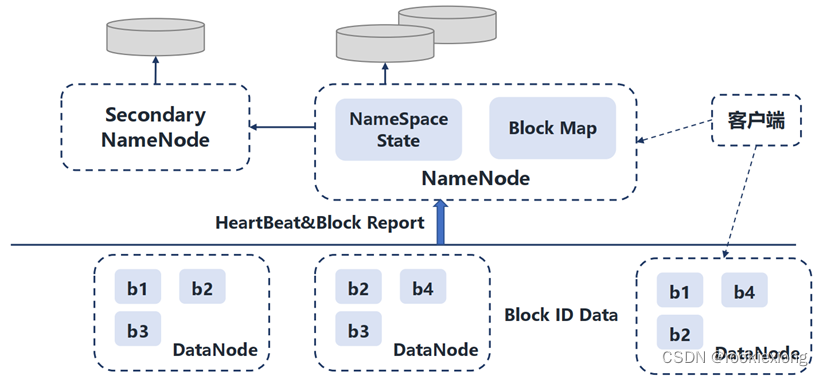
分布式计算平台 Hadoop 简介
Hadoop简介 Hadoop是一种分析和处理大数据的软件平台,是一个用Java语言实现的Apache的开源软件框架,在大量计算机组成的集群中实现了对海量数据的分布式计算。其主要采用MapReduce分布式计算框架,包括根据GFS原理开发的分布式文件系统HDFS、…...

系统学习Python——警告信息的控制模块warnings:常见函数-[warnings.warn]
分类目录:《系统学习Python》总目录 warnings.warn(message, categoryNone, stacklevel1, sourceNone, \*, skip_file_prefixesNone)常备用于引发警告、忽略或者触发异常。 如果给出category参数,则必须是警告类别类 ;默认为UserWarning。 或…...

监听键盘事件vue3封装hooks
监听页面键盘事件,执行对应方法 使用第三方API:vueuse 我封装的: 1. useKeyboardEvent.ts import { useMagicKeys } from vueuse/coreexport function enterKey(f: Function) {const { enter } useMagicKeys()watch(enter, v > {if (…...

Java Stream简化代码
使用原始流以获得更好的性能 使用 int、long 和 double 等基本类型时,请使用IntStream、LongStream 和 DoubleStream 等基本流,而不是 Integer、Long 和 Double 等装箱类型流。原始流可以通过避免装箱和拆箱的成本来提供更好的性能。 var array new i…...
py爬虫入门笔记(request.get的使用)
文章目录 Day11. 了解浏览器开发者工具2. Get请求http://baidu.com3. Post请求https://fanyi.baidu.com/sug4. 肯德基小作业 Day21. 正则表达式2. 使用re模块3. 爬取豆瓣电影Top250的第一页4. 爬取豆瓣电影Top250所有的250部电影信息 Day31. xpath的使用2. 认识下载照片线程池的…...

openssl3.2 - 官方demo学习 - encode - rsa_encode.c
文章目录 openssl3.2 - 官方demo学习 - encode - rsa_encode.c概述笔记END openssl3.2 - 官方demo学习 - encode - rsa_encode.c 概述 命令行参数 server_priv_key.pem client_priv_key.pem 这2个证书是前面certs目录里面做的 官方这个程序有bug, 给出2个证书, 还要从屏幕上输…...
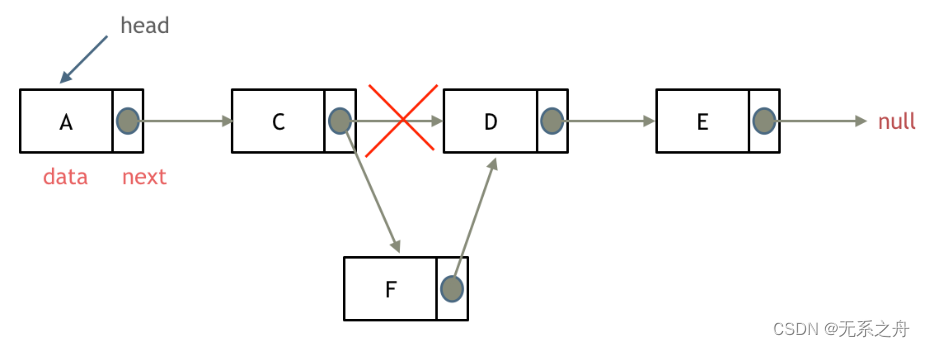
Day03
今日任务 链表理论基础203.移除链表元素707.设计链表206.反转链表 链表理论基础 1)单链表 单链表中的指针域只能指向节点的下一个节点 2)双链表 双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个…...

adb 常用命令汇总
目录 adb 常用命令 1、显示已连接的设备列表 2、进入设备 3、安装 APK 文件到设备 4、卸载指定包名的应用 5、从设备中复制文件到本地 6、将本地文件复制到设备 7、查看设备日志信息 8、重启设备 9、截取设备屏幕截图 10、屏幕分辨率 11、屏幕密度 12、显示设备的…...
ubuntu 2022.04 安装vcs2018和verdi2018
主要参考网站朋友们的作业。 安装时参考: ubuntu18.04安装vcs、verdi2018_ubuntu安装vcs-CSDN博客https://blog.csdn.net/qq_24287711/article/details/130017583 编译时参考: 【ASIC】VCS报Error-[VCS_COM_UNE] Cannot find VCS compiler解决方法_e…...

品牌推广与情绪价值的深度结合:市场大局下的新趋势与“准”原则
随着社会经济的快速发展和消费者心理的复杂化,品牌推广已经不再是单一的信息传递,而是一个与消费者建立情感连接、传达品牌价值的过程。在这个过程中,情绪价值起到了至关重要的作用。它不仅影响着消费者的购买决策,更是品牌与消费…...

React16源码: React中的不同的expirationTime的源码实现
不同的 expirationTime 1 )概述 在React中不仅仅有异步任务大部分情况下都是同步的任务,所以会有不同 expirationTime 的存在 2 )种类 A. Sync 模式,优先级最高 任务创建完成之后,立马更新到真正的dom里面是一个创建…...
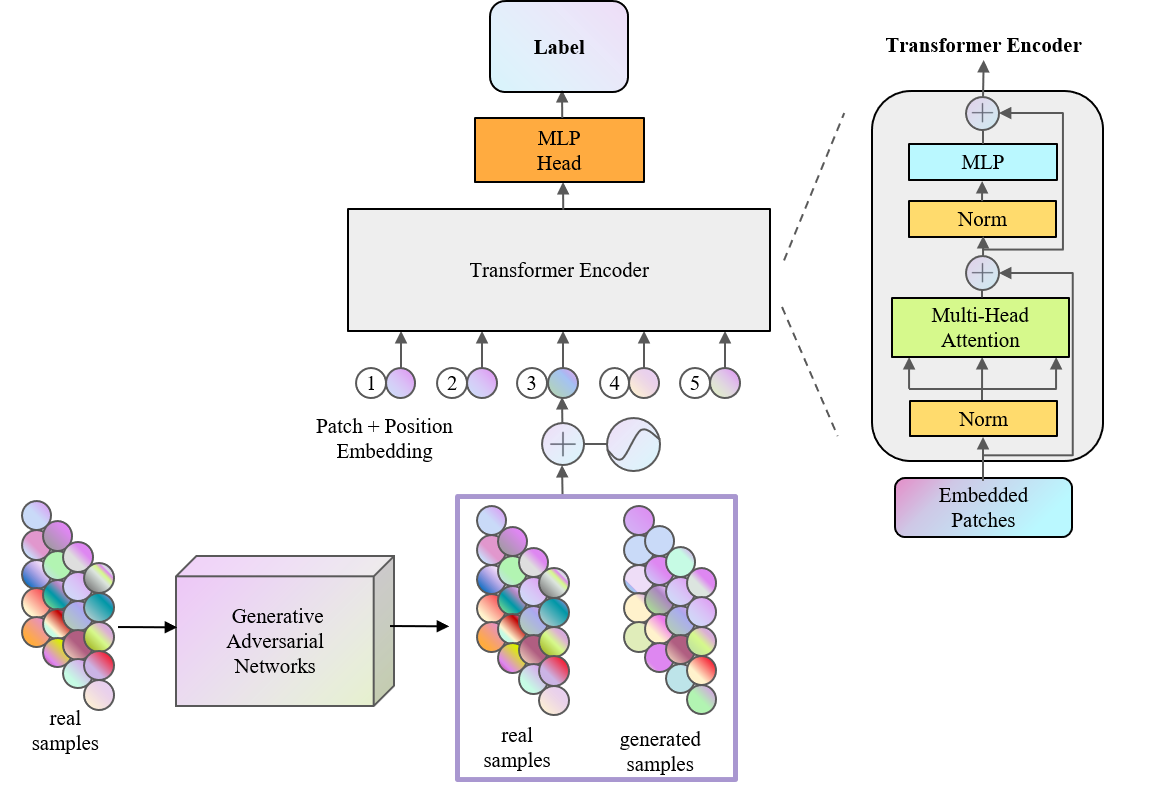
TRB 2024论文分享:基于生成对抗网络和Transformer模型的交通事件检测混合模型
TRB(Transportation Research Board,美国交通研究委员会,简称TRB)会议是交通研究领域知名度最高学术会议之一,近年来的参会人数已经超过了2万名,是参与人数和国家最多的学术盛会。TRB会议几乎涵盖了交通领域…...

Golang 打包
构建/打包 使用 Go 的构建命令: go build在包含 main 函数的包的目录下执行,它会生成一个可执行文件。文件名默认与包所在的目录名相同,但也可以使用 -o 选项来指定输出的文件名 交叉编译 Windows 环境下进行交叉编译以构建其他平台的可执…...

力扣每日一练(24-1-14)
做过类似的题,一眼就是双指针,刚好也就是题解。 if not nums:return 0p1 0 for p2 in range(1, len(nums)):if nums[p2] ! nums[p1]:p1 1nums[p1] nums[p2]return p1 1 根据规律,重复的数字必定相连,那么只要下一个数字与上一…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
