曲线生成 | 图解贝塞尔曲线生成原理(附ROS C++/Python/Matlab仿真)
目录
- 0 专栏介绍
- 1 贝塞尔曲线的应用
- 2 图解贝塞尔曲线
- 3 贝塞尔曲线的性质
- 4 算法仿真
- 4.1 ROS C++仿真
- 4.2 Python仿真
- 4.3 Matlab仿真
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 贝塞尔曲线的应用
贝塞尔曲线是一种数学曲线,由法国数学家皮埃尔·贝塞尔于1962年引入。它使用一组控制点来定义曲线的形状,这些控制点的位置和数量决定了曲线的特征。贝塞尔曲线的应用非常广泛:
- 计算机图形学:贝塞尔曲线可以用于绘制平滑的曲线和曲面。在计算机图形学中,它们被广泛用于绘制二维和三维图形对象,如曲线、路径、字体等。贝塞尔曲线具有良好的平滑性和灵活性,在图形渲染和模型构建方面发挥着重要作用;
- CAD 设计:贝塞尔曲线在计算机辅助设计中起到关键作用。设计师可以使用贝塞尔曲线创建和编辑复杂的曲线形状,如汽车外形、船体曲线、建筑物外观等。贝塞尔曲线的控制点可以通过拖动和调整来改变曲线的形状,使设计过程更加灵活和直观;
- 动画和游戏开发:贝塞尔曲线提供了一种方便的方法来定义和控制动画路径和运动轨迹。动画师可以使用贝塞尔曲线来创建平滑的动画路径,让角色和物体按照指定的路径移动。在游戏开发中,贝塞尔曲线也常用于实现精确的物体运动轨迹和碰撞检测;
- 字体设计:贝塞尔曲线被广泛应用于字体设计中。每个字母、数字或符号都可以由一组贝塞尔曲线组成,通过调整和连接这些曲线,可以创建出各种字体形状和风格。贝塞尔曲线的灵活性使得字体设计者能够轻松地创建出各种自然流畅的字符形状。
2 图解贝塞尔曲线
设平面上存在 n n n个离散的控制节点,则贝塞尔曲线的阶数为 n − 1 n-1 n−1。这 n n n个节点按某个顺序依次联结形成特征多边形,一个特征多边形将递归地确定一条以比例系数 t ∈ [ 0 , 1 ] t \in [0,1 ] t∈[0,1]为参数的贝塞尔曲线。

如图所示为1阶贝塞尔曲线的生成过程,具体地,对于一阶贝塞尔曲线有
P 1 ( t ) = ( 1 − t ) p 0 + t p 1 \boldsymbol{P}_1\left( t \right) =\left( 1-t \right) \boldsymbol{p}_0+t\boldsymbol{p}_1 P1(t)=(1−t)p0+tp1
其中控制节点 p i = [ x i , y i ] T \boldsymbol{p}_i=\left[ x_i,y_i \right] ^T pi=[xi,yi]T。
对于二阶贝塞尔曲线,首先给定比例系数 t ∈ [ 0 , 1 ] t \in [0,1 ] t∈[0,1],使
∣ p 0 a ∣ ∣ p 0 p 1 ∣ = ∣ p 1 b ∣ ∣ p 1 p 2 ∣ = ∣ a q ∣ ∣ a b ∣ \frac{|\boldsymbol{p}_0\boldsymbol{a}|}{|\boldsymbol{p}_0\boldsymbol{p}_1|}=\frac{|\boldsymbol{p}_1\boldsymbol{b}|}{|\boldsymbol{p}_1\boldsymbol{p}_2|}=\frac{|\boldsymbol{aq}|}{|\boldsymbol{ab}|} ∣p0p1∣∣p0a∣=∣p1p2∣∣p1b∣=∣ab∣∣aq∣
其中 q \boldsymbol{q} q落在由 a \boldsymbol{a} a、 b \boldsymbol{b} b确定的一阶贝塞尔曲线上, a \boldsymbol{a} a与 b \boldsymbol{b} b分别落在由 p 0 \boldsymbol{p}_0 p0、 p 1 \boldsymbol{p}_1 p1与 p 1 \boldsymbol{p}_1 p1、 p 2 \boldsymbol{p}_2 p2确定的一阶贝塞尔曲线上,因此 q \boldsymbol{q} q最终为二阶贝塞尔曲线上的一点,有
P 2 ( t ) = ( 1 − t ) a + t b \boldsymbol{P}_2\left( t \right) =\left( 1-t \right) \boldsymbol{a}+t\boldsymbol{b} P2(t)=(1−t)a+tb
即
P 2 ( t ) = ( 1 − t ) 2 p 0 + 2 t ( 1 − t ) p 1 + t 2 p 2 \boldsymbol{P}_2\left( t \right) =\left( 1-t \right) ^2\boldsymbol{p}_0+2t\left( 1-t \right) \boldsymbol{p}_1+t^2\boldsymbol{p}_2 P2(t)=(1−t)2p0+2t(1−t)p1+t2p2
如图所示

递推地,有
P ( t ) = ∑ i = 0 n − 1 p i B i , n − 1 ( t ) , t ∈ [ 0 , 1 ] \boldsymbol{P}\left( t \right) =\sum_{i=0}^{n-1}{\boldsymbol{p}_iB_{i,n-1}\left( t \right)}, t\in \left[ 0,1 \right] P(t)=i=0∑n−1piBi,n−1(t),t∈[0,1]
其中 p i ( i = 0 , ⋯ , n − 1 ) \boldsymbol{p}_i\left( i=0,\cdots ,n-1 \right) pi(i=0,⋯,n−1)为控制节点的有序序列, B i , n ( t ) = C n i t i ( 1 − t ) n − i , t ∈ [ 0 , 1 ] B_{i,n}\left( t \right) =C_{n}^{i}t^i\left( 1-t \right) ^{n-i},t\in \left[ 0,1 \right] Bi,n(t)=Cniti(1−t)n−i,t∈[0,1]称为伯恩斯坦多项式(Bernstein Polynomial),可视为权重因子,即曲线上某点 P ( t ) \boldsymbol{P}\left( t \right) P(t)是控制节点序列的加权平均
3 贝塞尔曲线的性质
贝塞尔曲线具有非常多优良的性质,主要列举如下
- 归一性:各项系数和为1
- 凸包性:贝塞尔曲线始终被所有控制点形成的最小凸多边形所包含
- 端点性:由于 B 0 , n ( 0 ) = B n , n ( 1 ) = 1 B_{0,n}\left( 0 \right) =B_{n,n}\left( 1 \right) =1 B0,n(0)=Bn,n(1)=1,所以贝塞尔曲线始于 p 0 \boldsymbol{p}_0 p0终于 p n \boldsymbol{p}_n pn,但不经过中间控制节点,即为逼近而非插值
- 几何不变性:贝塞尔曲线的形状仅与特征多边形各顶点相对位置有关,与坐标系的选择无关
- 变差伸缩性:若贝塞尔曲线特征多边形是一个平面图形,则平面内任意直线与贝塞尔曲线交点的个数不多于该直线与特征多边形的交点个数
- 微分: P ′ ( t ) = n ∑ i = 1 n ( p i − p i − 1 ) B i − 1 , n − 1 ( t ) \boldsymbol{P}'\left( t \right) =n\sum\nolimits_{i=1}^n{\left( \boldsymbol{p}_i-\boldsymbol{p}_{i-1} \right) B_{i-1,n-1}\left( t \right)} P′(t)=n∑i=1n(pi−pi−1)Bi−1,n−1(t),即 n n n阶贝塞尔曲线的导数是 n − 1 n-1 n−1阶贝塞尔曲线,控制节点为 q i = n ( p i + 1 − p i ) , i = 0 , ⋯ , n − 1 \boldsymbol{q}_i=n\left( \boldsymbol{p}_{i+1}-\boldsymbol{p}_i \right) , i=0,\cdots ,n-1 qi=n(pi+1−pi),i=0,⋯,n−1。特别地, P ′ ( 0 ) = n ( p 1 − p 0 ) \boldsymbol{P}'\left( 0 \right) =n\left( \boldsymbol{p}_1-\boldsymbol{p}_0 \right) P′(0)=n(p1−p0)、 P ′ ( 1 ) = n ( p n − p n − 1 ) \boldsymbol{P}'\left( 1 \right) =n\left( \boldsymbol{p}_n-\boldsymbol{p}_{n-1} \right) P′(1)=n(pn−pn−1),即贝塞尔曲线首末位置切线方向与特征多边形首末边方向一致
4 算法仿真
4.1 ROS C++仿真
核心代码如下
Points2d Bezier::generation(Pose2d start, Pose2d goal)
{double sx, sy, syaw;double gx, gy, gyaw;std::tie(sx, sy, syaw) = start;std::tie(gx, gy, gyaw) = goal;int n_points = (int)(helper::dist(Point2d(sx, sy), Point2d(gx, gy)) / step_);Points2d control_pts = getControlPoints(start, goal);Points2d points;for (size_t i = 0; i < n_points; i++){double t = (double)(i) / (double)(n_points - 1);points.push_back(bezier(t, control_pts));}return points;
}
其中bezier函数实现了伯恩斯坦多项式求和
Point2d Bezier::bezier(double t, Points2d control_pts)
{size_t n = control_pts.size() - 1;Point2d pt(0, 0);for (size_t i = 0; i < n + 1; i++){pt.first += _comb(n, i) * std::pow(t, i) * std::pow(1 - t, n - i) * control_pts[i].first;pt.second += _comb(n, i) * std::pow(t, i) * std::pow(1 - t, n - i) * control_pts[i].second;}return pt;
}
4.2 Python仿真
核心代码如下所示
def generation(self, start_pose: tuple, goal_pose: tuple):sx, sy, _ = start_posegx, gy, _ = goal_posen_points = int(np.hypot(sx - gx, sy - gy) / self.step)control_points = self.getControlPoints(start_pose, goal_pose)return [self.bezier(t, control_points) for t in np.linspace(0, 1, n_points)], \control_points
def bezier(self, t: float, control_points: list) ->np.ndarray:n = len(control_points) - 1control_points = np.array(control_points)return np.sum([comb(n, i) * t ** i * (1 - t) ** (n - i) * control_points[i] for i in range(n + 1)], axis=0)

4.3 Matlab仿真
核心代码如下所示
function curve = generation(start, goal, param)sx = start(1); sy = start(2);gx = goal(1); gy = goal(2);n_points = hypot(sx - gx, sy - gy) / param.step;control_pts = getControlPoints(start, goal, param);curve = [];for t=0:1 / n_points:1curve = [curve; bezier(t, control_pts)];end
end
function curve_pt = bezier(t, control_pts)[m, ~] = size(control_pts);n = m - 1;pt_x = 0; pt_y = 0;for i=0:npt_x = pt_x + nchoosek(n, i) * power(t, i) * power(1 - t, n - i) * control_pts(i + 1, 1);pt_y = pt_y + nchoosek(n, i) * power(t, i) * power(1 - t, n - i) * control_pts(i + 1, 2);endcurve_pt = [pt_x, pt_y];
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

曲线生成 | 图解贝塞尔曲线生成原理(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 贝塞尔曲线的应用2 图解贝塞尔曲线3 贝塞尔曲线的性质4 算法仿真4.1 ROS C仿真4.2 Python仿真4.3 Matlab仿真 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法…...

【一万字干货】一篇给你讲清楚智慧城市——附送智慧系列开发项目合集
智慧城市的概念 智慧城市(Smart City)起源于传媒领域,是指利用各种信息技术或创新概念,将城市的系统和服务打通、集成,以提升资源运用的效率,优化城市管理和服务,以及改善市民生活质量。 中国…...

关于如何禁用、暂停或退出OneDrive等操作,看这篇文件就够了
想知道如何禁用OneDrive?你可以暂停OneDrive的文件同步,退出应用程序,阻止它在启动时打开,或者永远从你的机器上删除该应用程序。我们将向你展示如何在Windows计算机上完成所有这些操作。 如何在Windows上关闭OneDrive 有多种方法可以防止OneDrive在你的电脑上妨碍你。…...
Vue3-46-Pinia-获取全局状态变量的方式
使用说明 在 Pinia 中,获取状态变量的方式非常的简单 : 就和使用对象一样。 使用思路 : 1、导入Store;2、声明Store对象;3、使用对象。 在逻辑代码中使用 但是 Option Store 和 Setup Store 两种方式定义的全局状态变量…...

数据库——DAY1(Linux上安装MySQL8.0.35(网络仓库安装))
一、环境部署 1、Red Hat Enterprise Linux 9.3 64 位 2、删除之前安装过本地镜像版本的MySQL软件(以前未安装过,请跳过此步骤) [rootlocalhost ~]# dnf remove mysql-server -y [rootlocalhost ~]# rm -rf /var/lib/mysql [rootlocalhost …...
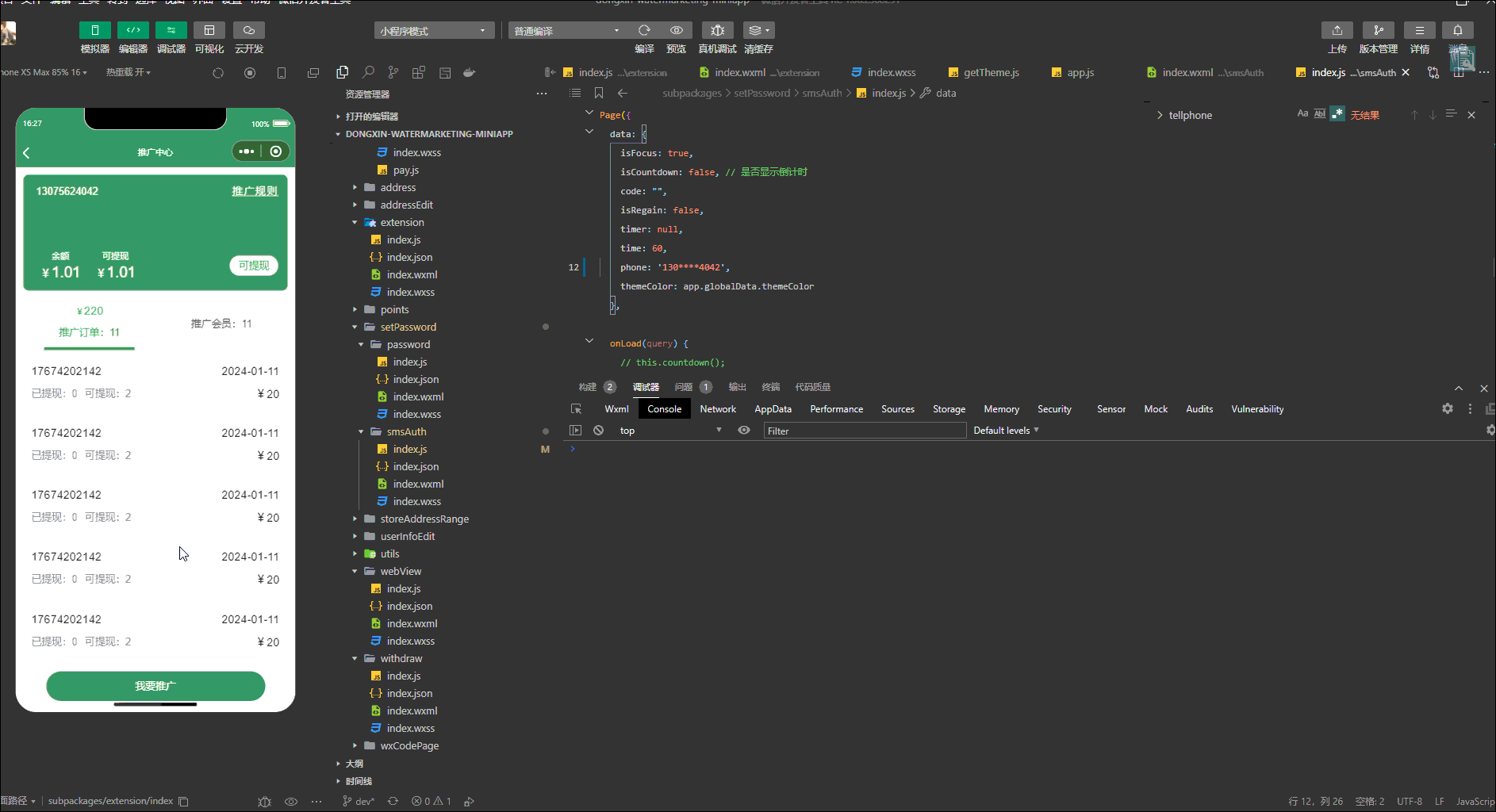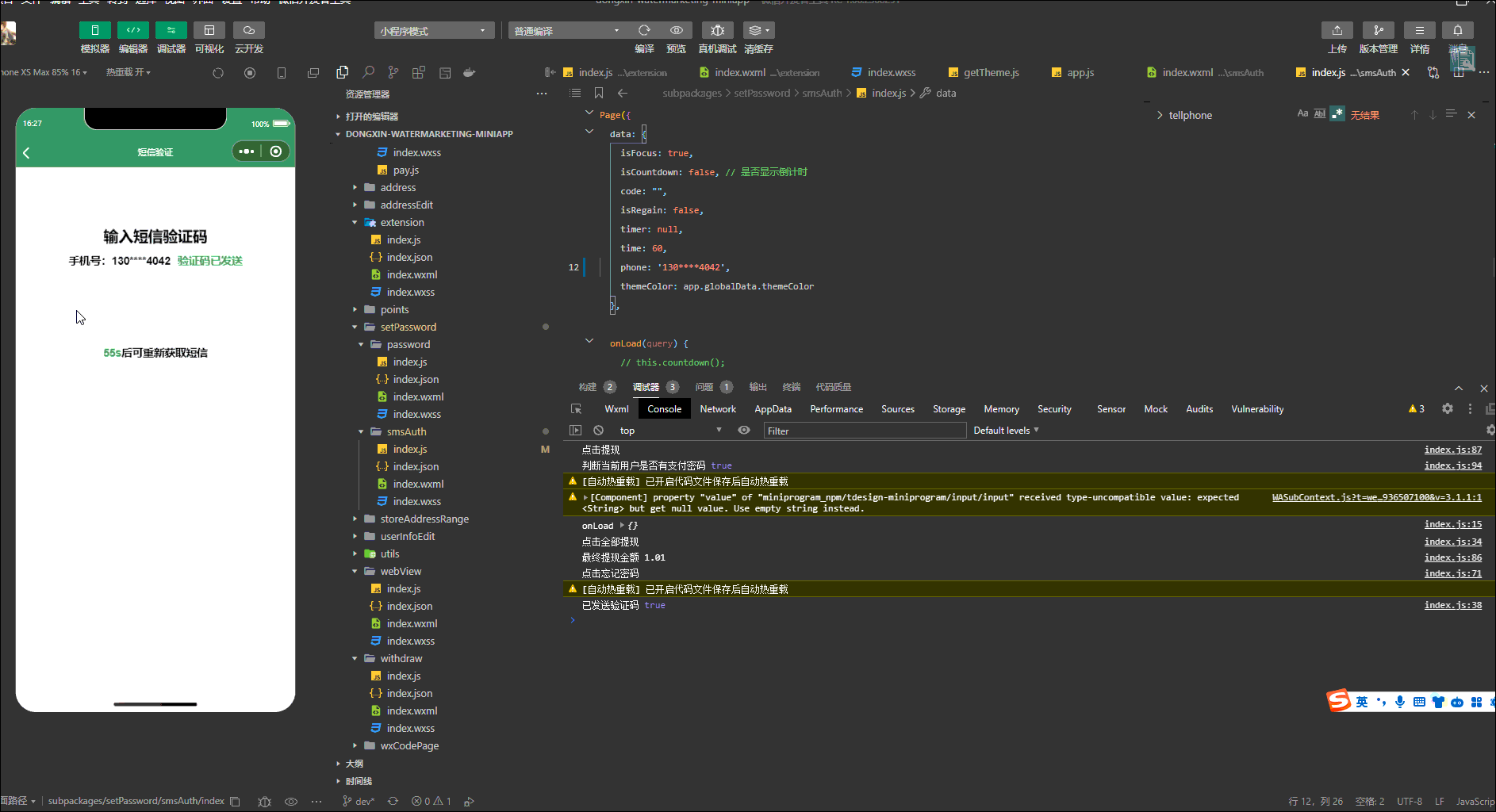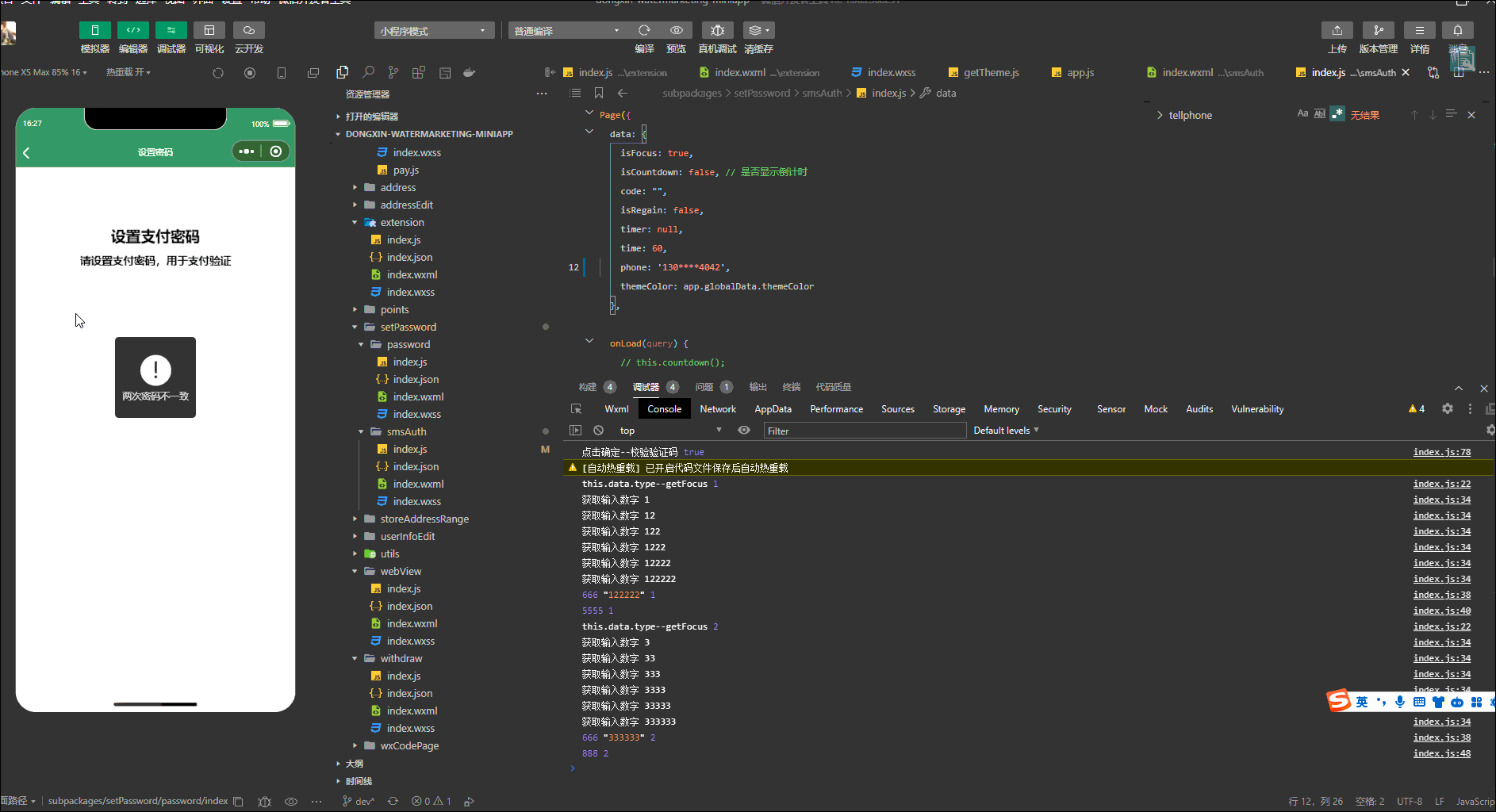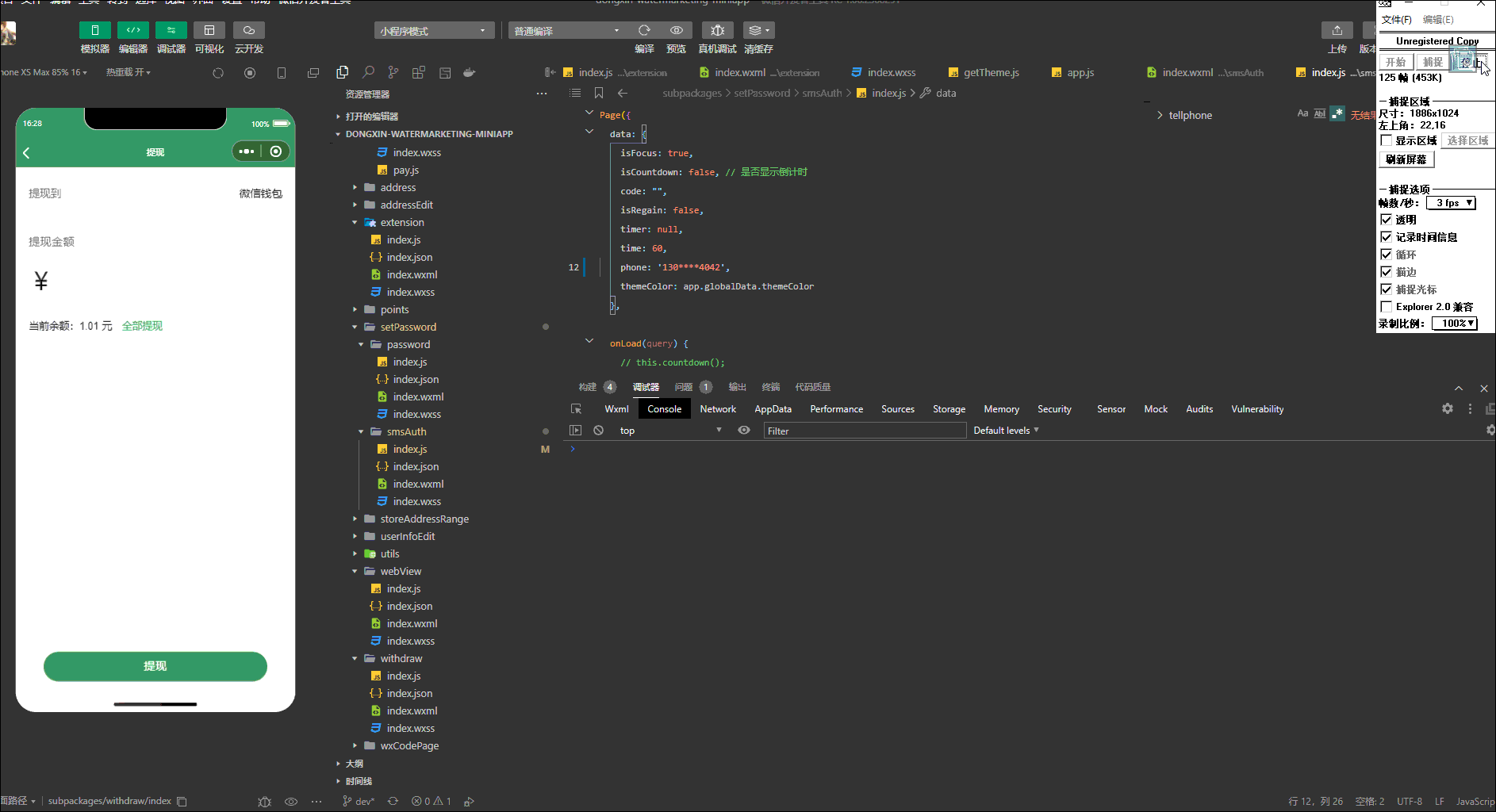
原生微信小程序-两次设置支付密码校验,密码设置二次确认
效果 具体代码 1、wxml <view style"{{themeColor}}"><view classcontainer><view class"password_content"><view wx:if{{type 1}}><view class"title"><view class"main_title">设置支付密码…...

【Python学习】Python学习15-模块
目录 【Python学习】Python学习15-模块 前言创建语法引入模块from…import 语句from…import* 语句搜索路径PYTHONPATH 变量-*- coding: UTF-8 -*-导入模块现在可以调用模块里包含的函数了PYTHONPATH 变量命名空间和作用域dir()函数globals() 和 locals() 函数reload() 函数Py…...
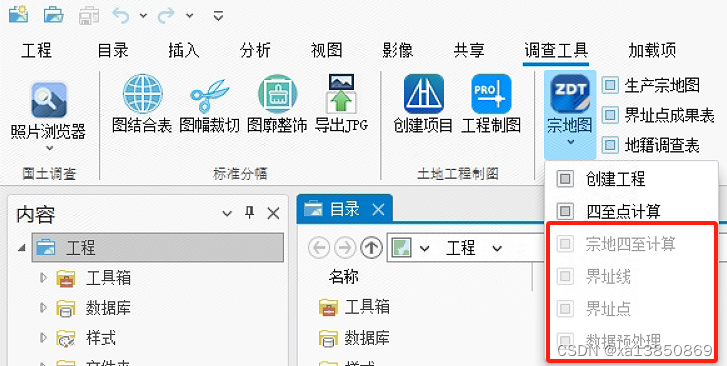
ARCGIS PRO SDK 设置UI控件状态:启用/禁用
举例: 第一步:添加两个 Button 分别命名为Connect、Disconnect 第二步:nfig.daml添加状态和条件:在 DAML 中定义条件。请记住,条件存在于模块标记<modules>之外,下代码定义:Disconnected_…...
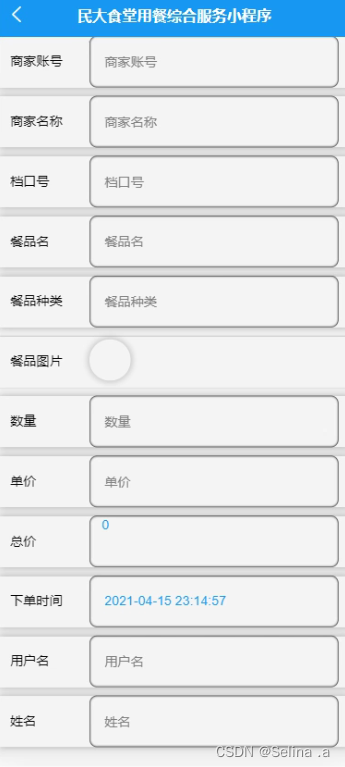
案例126:基于微信小程序的民大食堂用餐综合服务平台
文末获取源码 开发语言:Java 框架:SSM JDK版本:JDK1.8 数据库:mysql 5.7 开发软件:eclipse/myeclipse/idea Maven包:Maven3.5.4 小程序框架:uniapp 小程序开发软件:HBuilder X 小程序…...

cephfs 配置 mds stancd replay 操作
目的 1 假设有某个客户创建过千万文件目录,可以导致 ceph-mds 故障 2 backup ceph-mds 拉起时需要从内存中 replay 最后操作,可能需要吧当前目录中所有目> 录结构 重新 reload 至内存 3 这个过程可能需要几小时,可能需要几天 4 为了快速地拉起 ceph-mds 5 可以选择配置一…...

【2023我的编程之旅】系统学习C语言easyx图形库心得体会
目录 引言 C语言基础知识回顾 easyx图形库介绍 如何快速学习easyx图形库 学习笔记积累 学习成果展示 学习拓展 总结 引言 首先说一下我为什么要学习C语言easyx图形库。我接触C语言easyx图形库是在我今年一月份的时候,也是机缘巧合之下偶然在B站上看到了鸣人…...
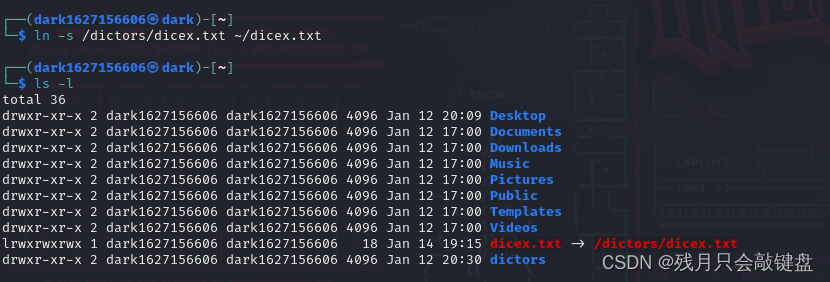
【linux】软链接创建(linux的快捷方式创建)
软连接的概念 类似于windows系统中的快捷方式。有的文件目录很长或者每次使用都要找很不方便,于是可以用类似windows的快捷方式的软链接在home(初始目录类似于桌面)上创建一些软链接方便使用。 软链接的语法 ln -s 参数1 参数2 参数1&#…...

基于BP神经网络的光伏发电预测
目录 摘要 BP神经网络参数设置及各种函数选择 参数设置 训练函数 传递函数 学习函数 性能函数 显示函数 前向网络创建函数 BP神经网络训练窗口详解 训练窗口例样 训练窗口四部详解 基于BP神经网络的租金预测 代码下载:19-66天气预测光伏发电.rar(代码完整,数据齐全)资源-C…...
RPA财务机器人在厦门市海沧医院财务管理流程优化汇总的应用RPA全球生态 2024-01-05 17:27 发表于河北
目前国内外研究人员对于RPA机器人在财务管理流程优化领域中的应用研究层出不穷,但现有研究成果主要集中在财务业务单一领域,缺乏财务管理整体流程一体化管控的研究。RPA机器人的功能绝非单一的财务业务处理,无论从自身技术发展,或…...

应用在LCD显示器电源插头里的氮化镓(GaN)MTC-65W1C
LCD(Liquid Crystal Display)显示器是利用液晶显示技术来进行图像表现的显示装置,从液晶显示器的结构来看,无论是笔记本电脑还是桌面系统,采用的LCD显示屏都是由不同部分组成的分层结构。LCD显示器按照控制方式不同可分…...

Vue新手村(二)
目录 1、计算属性 2、事件修饰符 2.1、stop事件修饰符 2.2、prevent事件修饰符 2.3、self事件修饰符 2.4、once事件修饰符 3、按键修饰符 3.1、enter回车键 1、计算属性 计算属性: computed:vue官方提供一个计算属性作用:在完成某种业…...

Mysql-redoLog
Redo Log redo log进行刷盘的效率要远高于数据页刷盘,具体表现如下 redo log体积小,只记录了哪一页修改的内容,因此体积小,刷盘快 redo log是一直往末尾进行追加,属于顺序IO。效率显然比随机IO来的快Redo log 格式 在MySQL的InnoDB存储引擎中,redo log(重做日志)被用…...

编程笔记 html5cssjs 039 CSS背景示例
编程笔记 html5&css&js 039 CSS背景示例 一、html二、css小结 网页上只有三个水平并列大小相同的的DIV,大小为300p*200,如何使用CSS让它们整体水平和垂直都居中,并使用不同的背景色? 一、html 要在网页上实现三个水平并列且大小相同…...

沃尔玛如何通过安全、有效的测评补单提升产品权重?
在沃尔玛的众多卖家之中,如何让自己脱颖而出?这不仅需要我们提供具有竞争力的价格,更需要我们提升产品的评分和权重。要让更多的客户注意到我们的产品,补单测评或许是一种有效的策略。尤其在新品上架初期,由于缺乏好评…...
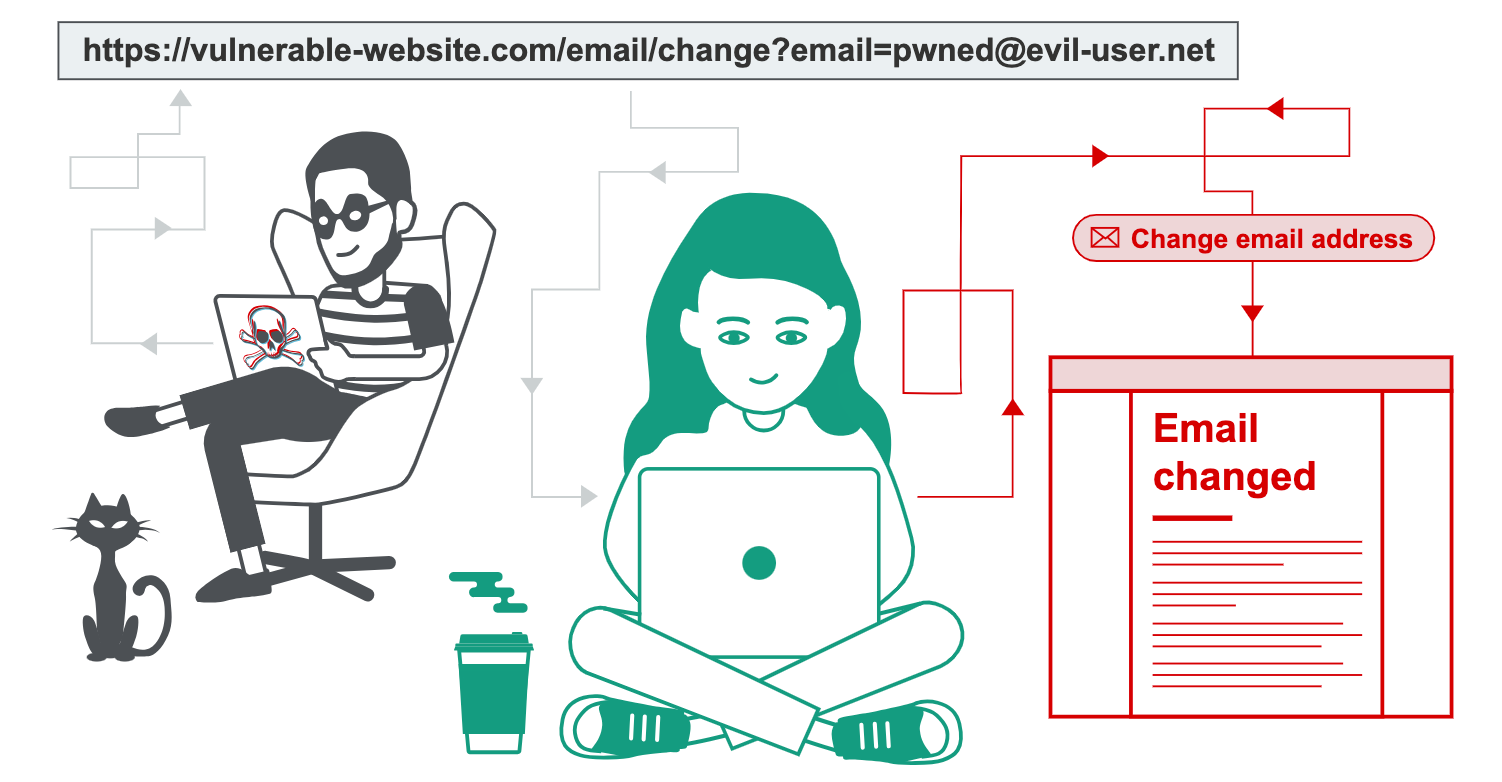
「 典型安全漏洞系列 」03.跨站请求伪造CSRF详解
引言:CSRF(Cross-Site Request Forgery,跨站请求伪造)是一种攻击技术,通过使用用户的身份进行不诚实地操作,恶意用户可以在受害者(目标)的机器上执行一些未授权的操作。这可能会危及…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
