什么是欧拉筛??
欧拉筛(Euler's Sieve),又称线性筛法或欧拉线性筛,是一种高效筛选素数的方法。它的核心思想是从小到大遍历每个数,同时标记其倍数为合数,但每个合数只被其最小的质因数标记一次,从而避免了重复标记,实现了线性时间复杂度的素数筛选。
以下是一个使用 Python 实现的欧拉筛的例子:
def euler_sieve(n): # 初始化标记数组,默认所有数都是素数(未标记) is_prime = [True] * (n + 1) is_prime[0] = is_prime[1] = False primes = [] # 用于存储素数 for i in range(2, n + 1): if is_prime[i]: # i 是素数,将其加入素数列表 primes.append(i) # 标记 i 的倍数为合数 for j in range(i * i, n + 1, i): is_prime[j] = False return primes # 示例:找出 100 以内的素数
primes_up_to_100 = euler_sieve(100)
print(primes_up_to_100)在这段代码中,euler_sieve 函数接受一个整数 n 作为参数,返回小于等于 n 的所有素数的列表。函数内部首先创建了一个布尔数组 is_prime,用于标记每个数是否为素数。然后,函数从 2 开始遍历到 n,对于每个遍历到的数 i,如果 is_prime[i] 为真,则将 i 加入到素数列表中,并标记 i 的所有倍数为合数(从 i * i 开始,因为比 i 小的数的倍数已经被之前的素数标记过了)。
最终,函数返回素数列表。在这个例子中,我们调用 euler_sieve(100) 来找出 100 以内的所有素数,并打印结果。
相关文章:

什么是欧拉筛??
欧拉筛(Eulers Sieve),又称线性筛法或欧拉线性筛,是一种高效筛选素数的方法。它的核心思想是从小到大遍历每个数,同时标记其倍数为合数,但每个合数只被其最小的质因数标记一次,从而避免了重复标…...
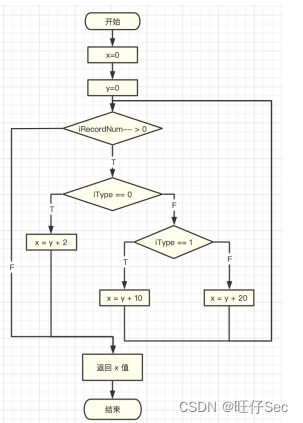
2023年全国职业院校技能大赛软件测试赛题—单元测试卷⑩
单元测试 一、任务要求 题目1:根据下列流程图编写程序实现相应处理,程序根据两个输入参数iRecordNum和IType计算x的值并返回。编写程序代码,使用JUnit框架编写测试类对编写的程序代码进行测试,测试类中设计最少的测试数据满足基路…...

使用WAF防御网络上的隐蔽威胁之SSRF攻击
服务器端请求伪造(SSRF)攻击是一种常见的网络安全威胁,它允许攻击者诱使服务器执行恶意请求。与跨站请求伪造(CSRF)相比,SSRF攻击针对的是服务器而不是用户。了解SSRF攻击的工作原理、如何防御它࿰…...
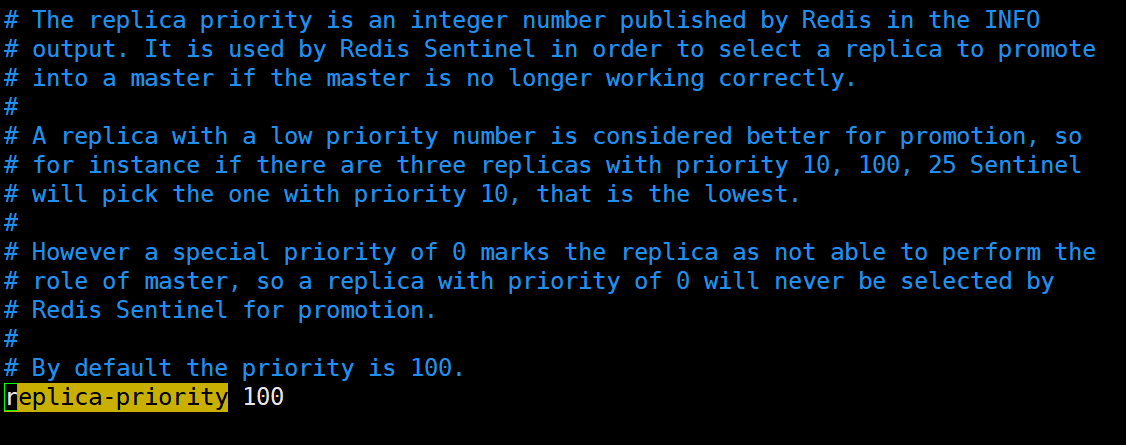
Redis基础系列-哨兵模式
Redis基础系列-哨兵模式 文章目录 Redis基础系列-哨兵模式1. 引言2. 什么是哨兵模式?3. 哨兵模式的配置4. 哨兵模式的启动和验证4.1 主master宕机,看会出现什么问题4.2 重启6379主机 5. 哨兵模式的工作原理和选举原理5.1. SDown主观下线(Subj…...
 Angular中的数据请求 与 路由)
【angular教程240112】09(完) Angular中的数据请求 与 路由
【angular教程240112】09(完) Angular中的数据请求 与 路由 目录标题 一、 Angular 请求数据简介0 使用Angular内置模块HttpClientModule和HttpClientJsonpModule:1 Angular中的GET请求:2 Angular中的POST请求:3 Angular中的JSONP请求:4使用Axios进行数据请求: 二、 详解 Angul…...

go中拷贝文件操作
一. 拷贝文件内容到另一个文件位置 // 拷贝文件内容到另一个文件里面 func copyContent() {filepath1 : "d:/abc.txt"filepath2 : "e:/eee.txt"// 读取内容data, err : os.ReadFile(filepath1) // 使用os.ReadFile函数读取指定路径的文件内容if err ! nil…...

未来气膜体育馆的发展趋势是什么?
未来气膜体育馆的发展趋势是多方面的,以下是其中几个方面的趋势。 起初,随着人们对体育运动的需求不断增加,气膜体育馆的建设和使用将成为一种趋势。气膜体育馆具有灵活性和可移动性的特点,可以快速搭建和拆除,能够适…...
)
通信扫盲(五)
系列文章目录 1 通信扫盲(一): 通信的本质、通信发展史-各代移动通信的多祉技术、5G、6G应用场景/愿景、LTE是什么?3GPP是什么? 链接:通信扫盲(一) 2 通信扫盲(二&…...

nbcio-boot项目的文件上传与回显处理方法
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: https://gitee.com/nbacheng/n…...

《动手学深度学习》学习笔记 第9章 现代循环神经网络
本系列为《动手学深度学习》学习笔记 书籍链接:动手学深度学习 笔记是从第四章开始,前面三章为基础知识,有需要的可以自己去看看 关于本系列笔记: 书里为了让读者更好的理解,有大篇幅的描述性的文字,内容很…...

「HDLBits题解」Vector100r
本专栏的目的是分享可以通过HDLBits仿真的Verilog代码 以提供参考 各位可同时参考我的代码和官方题解代码 或许会有所收益 题目链接:Vector100r - HDLBits module top_module( input [99:0] in,output [99:0] out );integer i ; always (*) beginfor (i 0 ; i <…...
如何制作专业商业画册,提升品牌形象
随着市场竞争的日益激烈,商业画册作为展示企业形象和产品特点的重要载体,越来越受到企业的重视。然而,如何制作一份专业、有吸引力的商业画册,提升品牌形象呢? 在制作商业画册之前,首先要明确目标受众。根…...
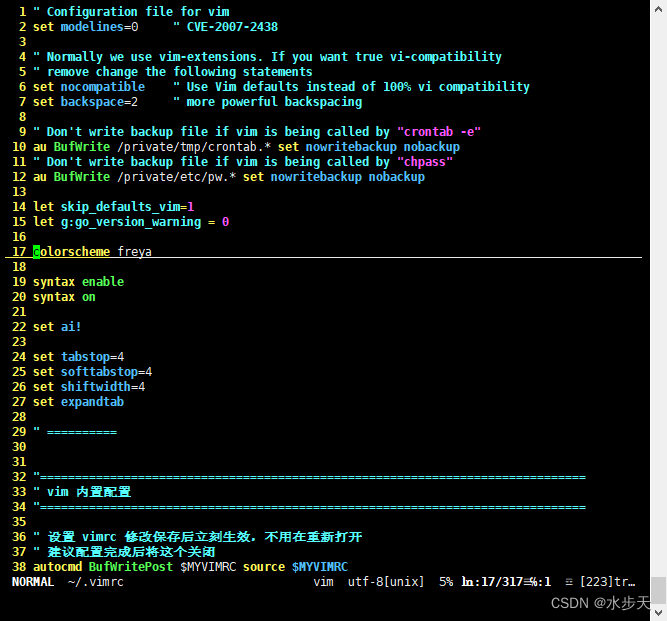
vim升级和配置
vim升级和配置 1、背景2、环境说明3、操作3.1 升级VIM3.2 配置VIM3.2.1、编辑vimrc文件3.2.2、安装插件 1、背景 日常工作跟linux系统打交道比较多,目前主要用到的是Cenots7和Ubuntu18这两个版本的linux系统,其中Centos7主要是服务器端,Ubun…...

java通过okhttp方式实现https请求的工具类(绕过证书验证)
目录 一、引入依赖包二、okhttp方式实现的https请求工具类2.1、跳过证书配置类2.2、okhttp方式的 https工具类 三、测试类 一、引入依赖包 引入相关依赖包 <!--okhttp依赖包--> <dependency><groupId>com.squareup.okhttp3</groupId><artifactId>…...

mysql定时备份shell脚本和还原
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言数据库备份分类mysqldump命令备份计划1.每日备份,保留30天备份文件2.每月1号备份,保留12个月备份文件 定时调度还原总结 前言 数据库备…...

DevOps搭建(十六)-Jenkins+K8s部署详细步骤
1、整体部署架构图 2、编写脚本 vi pipeline.yml apiVersion: apps/v1 kind: Deployment metadata:namespace: testname: pipelinelabels:app: pipeline spec:replicas: 2selector:matchLabels:app: pipelinetemplate:metadata:labels:app: pipelinespec:containers:- nam…...

WaitForSingleObject 函数的诸多用途与使用场景总结
目录 1、WaitForSingleObject函数详细说明 2、在线程函数中调用WaitForSingleObject实现Sleep,可立即退出Sleep状态 3、调用WaitForSingleObject函数监测线程或进程是否已经退出 3.1、子进程实时监测主进程是否已经退出,主进程退出了,则子…...
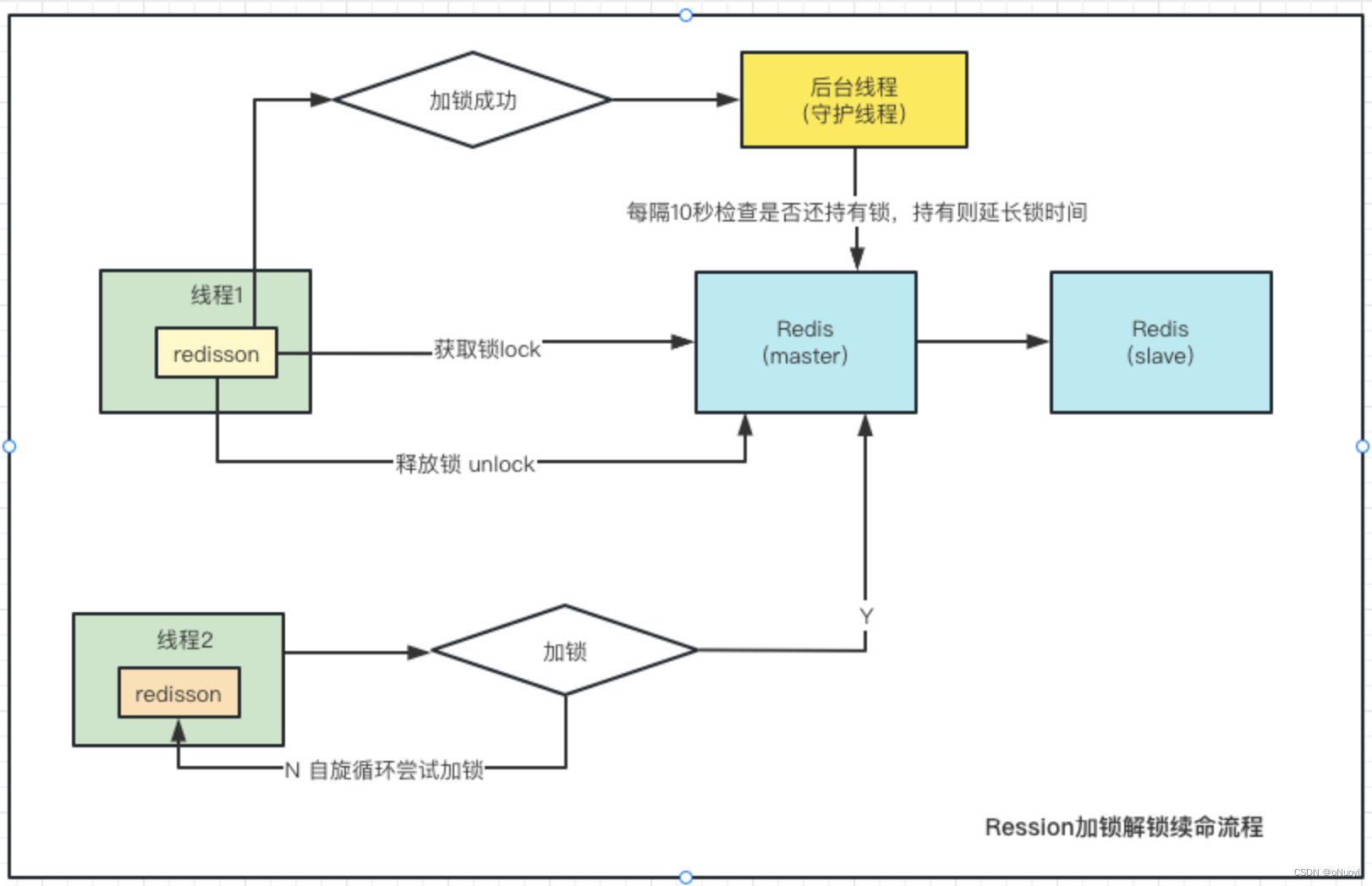
4、Redis高并发分布式锁实战
引言 在分布式系统中,保证数据的一致性和避免竞争条件是至关重要的。分布式锁是一种常用的机制,而Redis作为一款高性能的内存数据库,提供了简单而强大的分布式锁方案。本文将深入探讨如何利用Redis高并发分布式锁来解决分布式系统中的并发控…...

matlab subs 函数计算太慢
来源 计算机器人 transformation matrix 相关内容时,对于关节角度进行离散,循环计算很慢,随着角度划分越来越细,怎么提高速度是一个问题。 最优解决方法 fun_handle matlabFunction(T_t2b_RPY_tmp);T_t2b_RPY_tmp是 transform…...

如何确保网络传输的安全性和稳定性?
随着互联网的普及和数字化时代的到来,网络传输已经成为我们日常生活中不可或缺的一部分。无论是发送邮件、浏览网页、在线支付还是进行视频通话,都需要通过网络进行数据传输。然而,网络传输的安全性和稳定性问题也日益突出,如何确…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
