第十三届蓝桥杯
这里写目录标题
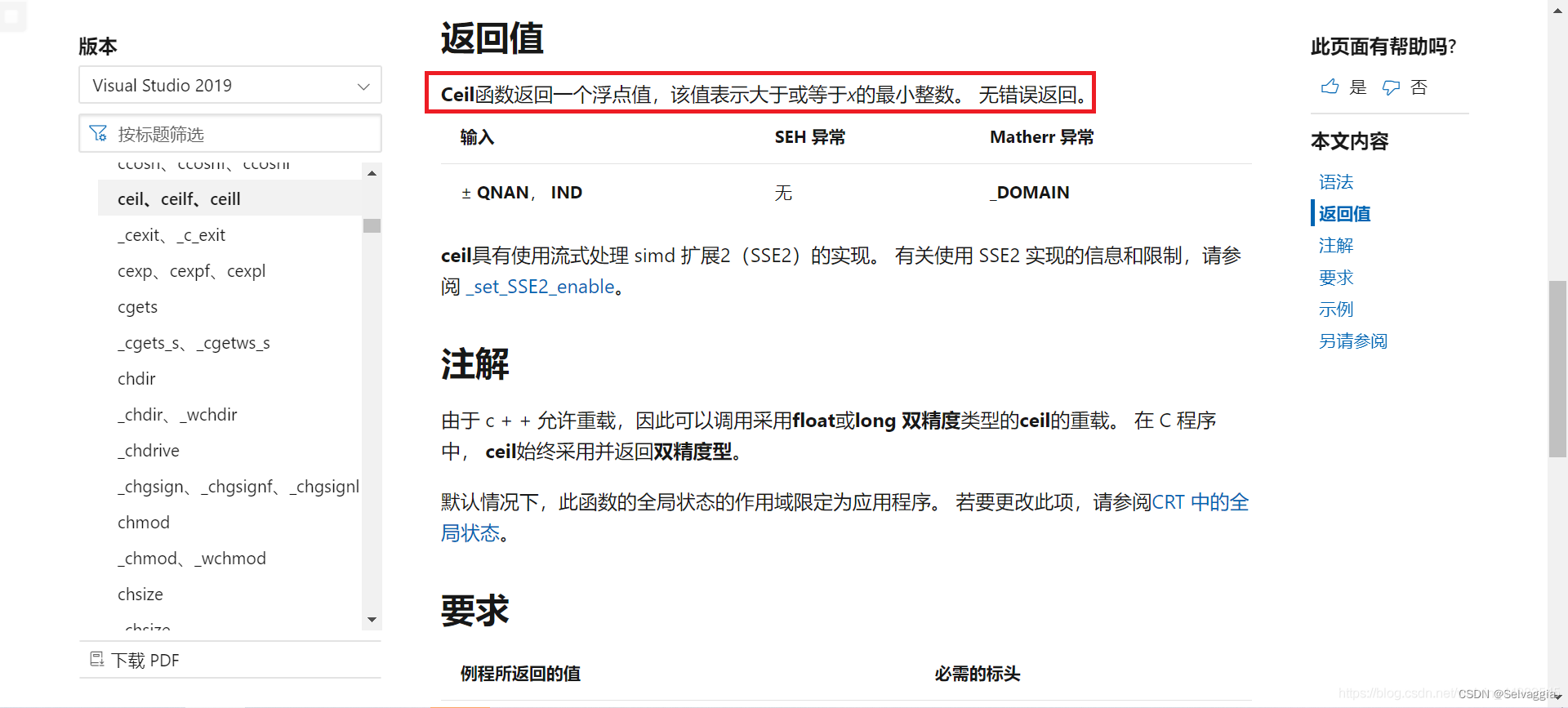
- 一、刷题统计(ceil函数返回的是等值于某最小整数的浮点值,不强制转换回int就wa,没错就连和int整数相加都wa
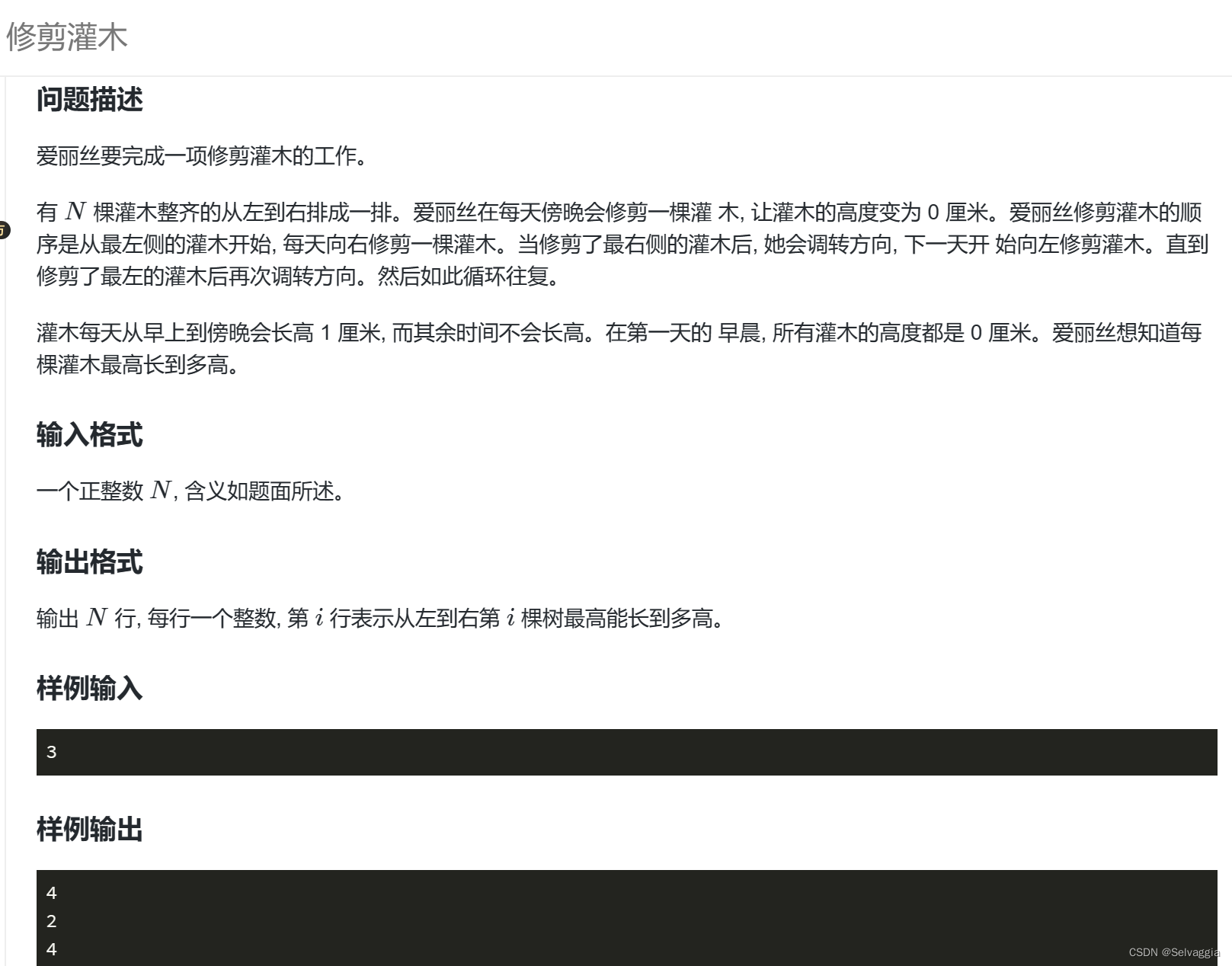
- 二、修剪灌木(主要应看清楚会调转方向
- 三、统计子矩阵(前缀和+滑动窗口⭐)
- 四、[积木画](https://www.lanqiao.cn/problems/2110/learning/)
- 顺子日期
- X进制减法
一、刷题统计(ceil函数返回的是等值于某最小整数的浮点值,不强制转换回int就wa,没错就连和int整数相加都wa

ceil函数我给你跪了,总之ceil(x) 返回的是 等值于 大于或等于x(一般为浮点数,可能是整数)的最小整数 的浮点数
#include <bits/stdc++.h>
using namespace std;
#define int long long int
signed main()
{
int res=0,sum=0;
int a,b,n;
cin>>a>>b>>n;int x=5*a+2*b;
res+=(n/x*7);
sum+=n/x*x;
int y=n-sum;
//x=0;
//while(y>0){
// x++;
// if(x<=5)y-=a;
// else y-=b;//}
//res+=x;
if(y>5*a){res=res+5+(int)ceil((y-5*a)*1.0/b);
}
else res+=(int)ceil(1.0*y/a);
//if(y>5*a){
// res+=5;
// int z=((y-5*a)%b==0)?(y-5*a)/b:(y-5*a)/b+1;
// res+=z;
//}
//else{
// int z=((y%a)==0)?y/a:y/a+1;
// res+=z;
//}
cout<<res;return 0;
}
二、修剪灌木(主要应看清楚会调转方向
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n;
const int N=10000;
int a[N];
int b[N];
signed main(){
//在第一天的 早晨, 所有灌木的高度都是 0 厘米 每天从早上到傍晩会长高 1 厘米
//当修剪了最右侧的灌木后, 她会调转方向
cin>>n;for(int i=1;i<=n;i++){a[i]=2*max(n-i,i-1);cout<<a[i]<<endl;} //3 4 5// 1 1 1 0 1 1
// 1 2 2 1 0 2
// 2 1 3 2 1 0
// 3 2 1 3 0 1
// 4 1 2 0 1 2
// 1 2 3 1 0 3
// 2 1 4 2 1 0// 首先容易发现,
// 1、最高的时候永远出现在晚上未修剪之前(马上要修剪了),轮流变成0
// 2、灌木的最高长度应该是对称的(调转方向)
// 3、因为有最高高度,这应该是个循环的固定模式,即每个灌木都是从0->max 重复
// 固定模式的哪个时刻出现最高高度呢?
// 刚把a[x]砍到0后,向左(或向右)走到底a[n],再往回走到a[x]的时候return 0;
}
三、统计子矩阵(前缀和+滑动窗口⭐)
结错婚是惨过输钱,看错题惨过。。。 是不超过k不是等于k啊大佬
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,m,k;
const int N=1005;
int a[N][N];
int b[N][N];//b[i][j],第i列 前j行的前缀和
int res=0;
void fun(int x,int y){int s[N];int sum[N];memset(s,sizeof(s),0);memset(sum,sizeof(sum),0);for(int i=1;i<=n;i++){s[i]=b[i][y]-b[i][x-1];sum[i]=sum[i-1]+s[i];}//这里是暴力枚举区间,在双重循环下暴力导致超时//用滑动窗口(maybe)
// for(int l=1;l<=n;l++){
// for(int r=l;r<=n;r++){
// if((sum[r]-sum[l-1])<=k)res++;
// }
// }int l=1,r=1;for(int r=l;r<=n;r++){while(sum[r]-sum[l-1]>k){l++;}res+=r-l+1;
//此时sum[r]-sum[l-1]<=k,由于枚举的是右端点,以r为右端点,有r-l+1个空间满足条件}
// l l+1 l+2 l+3 (l,l+3) (l+1,l+3) (l+2,l+3) (l+3,l+3)
}
void fun1(int i,int ii){
// 这里a[i][j]是第j列前i行的前缀和
//我的题解b[i][j]是第i列前j行的前缀和int l = 1, r = 1;//滑动窗口的左右端点int sum = 0;//区间前缀和:[l,r]区间的累计和for(r = 1; r <= n; r++)//遍历右端点,根据区间和调整左端点{sum += a[ii][r] - a[i-1][r];//加上右端点处的和while(sum > k)//区间和了,左端点右移,区间变小{sum -= a[ii][l] - a[i-1][l];//减去移出去的左端点处的和l++;}res += r - l + 1;//方法数就是找到的区间大小累加}
}
signed main(){cin>>m>>n>>k;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){cin>>a[i][j];b[j][i]=b[j][i-1]+a[i][j];}}
// 子矩阵的和
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m;j++){
// cout<<b[i][j]<<" ";
// }
// cout<<endl;
// } for(int i=1;i<=m;i++){for(int j=i;j<=m;j++){fun(i,j);}}cout<<res;return 0;
}
三个样例运行超时了
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,m,k;
const int N=1005;
int a[N][N];
int b[N][N];//b[i][j],第i列 前j行的前缀和
int res=0;
void fun(int x,int y){int s[N];int sum[N];memset(s,sizeof(s),0);memset(sum,sizeof(sum),0);for(int i=1;i<=n;i++){s[i]=b[i][y]-b[i][x-1];sum[i]=sum[i-1]+s[i];}for(int i=1;i<=n;i++){for(int j=i;j<=n;j++){if((sum[j]-sum[i-1])<=k)res++;}}}
signed main(){cin>>m>>n>>k;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){cin>>a[i][j];b[j][i]=b[j][i-1]+a[i][j];}}
// 子矩阵的和
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m;j++){
// cout<<b[i][j]<<" ";
// }
// cout<<endl;
// } for(int i=1;i<=m;i++){for(int j=i;j<=m;j++){fun(i,j);}}cout<<res;return 0;
}
四、积木画

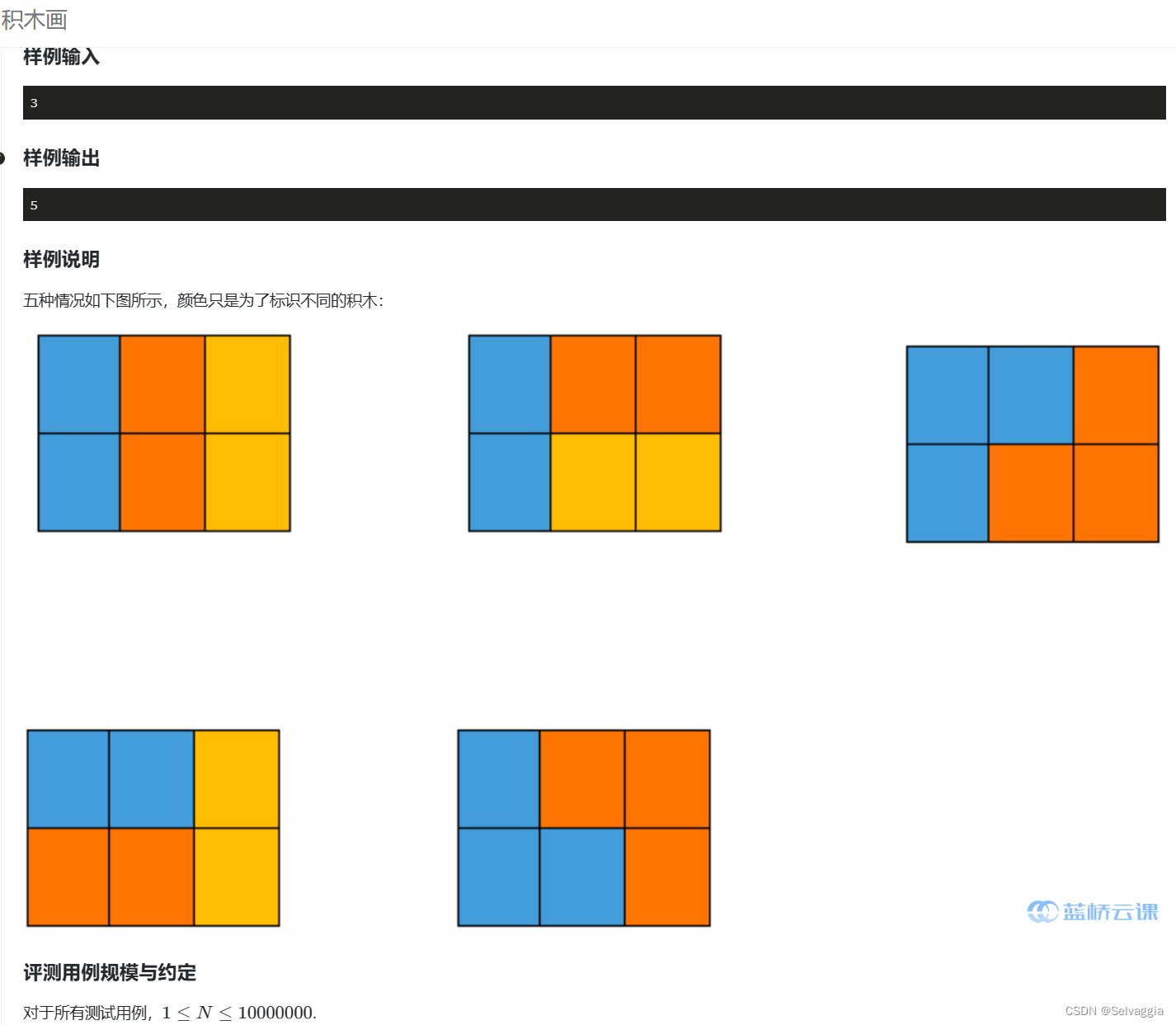
我一直以为我是对的来着(0%通过率,excuse me?呜呜呜)
fine,我看完n=3的情况下意识地以为 组合情况 要么 长方形单独拼,L形单独拼,或者是 长方形和L形混拼(而且下意识觉得两种混拼的形式只有n=3情况中枚举的这么几种),但显然简单化了(稍微动脑想想,n=5,一个L形两个长方形,这种组合情况就超出了n=3枚举的那些情况
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,m,k;
const int mod=1000000007;
const int N=10000005;
int dp[N];signed main(){cin>>n;dp[1]=1;dp[2]=2;dp[3]=5;for(int i=4;i<=n;i++){dp[i]=(dp[i-1]*1%mod+dp[i-2]*2%mod+dp[i-3]*5%mod)%mod;}cout<<dp[n];return 0;
}
递归还是讲究一个状态转移,那么对于第 iii 列可能会有哪几种情况呢?

(,阴影部分表示第 i−1i-1i−1 列已经拼好的状态,由于长方形和L形都只占两列,只需要观察第 i−1i-1i−1 列和第 iii 列)
最后所求的方案数 等值于 dp[n][4]dp[n][4]dp[n][4]
不用担心除了第n列之外的列上下没有被覆盖满,因为看我们的状态转移图,转移方式无一不会使得第 i−1i-1i−1 列存在未被覆盖的情况,由此拼图方式递推,推到第 iii 列时,不管第 iii 列状态咋样,第 i−1i-1i−1 列一定被覆盖满了
正当我以为我要AC的时候,没有一声不好意思,竟让我崩溃至此
当需要开很大的数组(这里高达 1e71e71e7 ),尽量不要开longlong,实在不行将中途结果用强制转化成longlong的方法防止爆int,其次就是空间本来就已经不够了,数组下标还是不要作妖从1开始,从0开始节省一点

这里给256M
一、数组太大,超内存
#define int long long int
const int N=10000005;
int dp[N][5];
vector<vector<int>> dp(n + 1, vector<int>(5));
数开八位的真敢啊你,清一色的runerror,以后超过六位数就用vector(等等, 不对,vector似乎更占空间,看这题最后的一块题解,同样不开long long,vector反而不行了,这里能过30%不过是因为是根据n的大小针对性开的,有部分测试样例n比较小
二、初始化
没错的,都是内存的错
dp[1][4]=1;dp[1][0]=1;
但为什么这个能过35%
即便避开了上面两个任意让人过%0的点,也只有勉强的30%
#include <bits/stdc++.h>
using namespace std;
#define int long long int
int n,m,k;
const int mod=1000000007;
// const int N=10000005;
// int dp[N][5];signed main(){cin>>n;vector<vector<int>> dp(n + 1, vector<int>(5));// dp[1][4]=1;// dp[1][0]=1;dp[0][4] = 1;for(int i=1;i<=n;i++){dp[i][1]=(dp[i-1][4])%mod;dp[i][2]=(dp[i-1][1]+dp[i-1][3])%mod;dp[i][3]=(dp[i-1][1]+dp[i-1][2])%mod;dp[i][4]=(dp[i-1][4]+dp[i-1][3]+dp[i-1][2]+dp[i-1][1])%mod;}cout<<dp[n][4];return 0;
}
AC代码 人已疯,仍然不知道在数组越界的情况下是怎么AC的,都要怀疑自己二维数组的表示一直以来是错的了
#include <bits/stdc++.h>
using namespace std;
#define LL long long int
int n,m,k;
const int mod=1000000007;
const int N=10000005;
LL dp[N][3];//改成4 变 35%,。全是超过内存限制signed main(){cin>>n;// vector<vector<LL>> dp(n + 1, vector<LL>(4));这种数组声明 30% 运行错误or超内存
//忘记LL直接0%,二维长度改成3 全军覆没0%,运行错误(数组越界
//难道两种数组声明二维长度的含义不同?dp[0][3] = 1;for (int i = 1; i <= n; i++) {dp[i][0] = dp[i - 1][3];dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % mod;dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % mod;dp[i][3] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][3]) % mod;}cout<< dp[n][3];return 0;
}
如果要是开long long 的dp,则会因为空间太大,错误。要是开int的dp数组,又会因为数据类型不够大,在多个int数据相加时,会超出int的范围,导致答案错误…
真正的解决办法
当需要开很大的数组(这里高达 1e81e81e8 ),尽量不要开longlong,实在不行将中途结果用强制转化成longlong的方法防止爆int,其次就是空间本来就已经不够了,数组下标还是不要作妖从1开始,从0开始节省一点
两种初始化方法都行
dp[1][0] = 1;dp[1][1] = 0;dp[1][2] = 0;dp[1][3] = 1;for(int i=2;i<=n;i++){
dp[0][3] = 1;for(int i=1;i<=n;i++){
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
int n,m,k;
const int mod=1000000007;const int N=10000005;int dp[N][4];signed main(){cin>>n;
// vector<vector<int>> dp(n + 1, vector<int>(4));
// dp[1][3]=1;
// dp[1][0]=1;dp[0][3] = 1;for(int i=1;i<=n;i++){dp[i][0]=((ll)dp[i-1][3])%mod;dp[i][1]=((ll)dp[i-1][0]+(ll)dp[i-1][2])%mod;dp[i][2]=((ll)dp[i-1][0]+(ll)dp[i-1][1])%mod;dp[i][3]=((ll)dp[i-1][3]+(ll)dp[i-1][2]+(ll)dp[i-1][1]+(ll)dp[i-1][0])%mod;}cout<<dp[n][3];return 0;
}
问题又来了,即使不开 longlong数组,这里用vector声明二维数组的时候又只能过35%,我不理解

力扣原题-动态规划解释
找规律解释(类似这种的动态规划找方法数都有规律?)
顺子日期
#include <iostream>
using namespace std;
int a[10];
int mon[15]={0,31,28,31,30,31,30,31,31,30,31,30,31};
bool ok(int x){int y=x/10000;int m=(x%10000)/100;int d=x%100;if(m<1||m>12)return false;if(d<1)return false;if(d>mon[m])return false;return true;
}
int main()
{int res=0;for(int i=20220101;i<=20221231;i++){if(!ok(i))continue;int cnt=0;int x=i;while(x){a[cnt++]=x%10;x/=10;}//翻转了,判断是否 321for(int j=0;j<6;j++){if(a[j+1]==a[j]-1&&a[j+2]==a[j]-2){res++;break;}}
}
cout<<res;return 0;
}
X进制减法

样例输入
11
3
10 4 0
3
1 2 0
样例输出
94


首先是找规律,第 iii 位的权重是累乘 111 ~ i−1i-1i−1 的所有进制
最小的差值,我下意识以为要暴力搜索所有权值的组合情况,因为毕竟虽然 A>=BA>=BA>=B ,难免可能统一位上 A[i]<B[i]A[i]<B[i]A[i]<B[i]
但也许是贪心思想,每一位都取最低的权值,就能得到最小的差值
暴力搜索版(过了30%,剩下的超时了)
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
const int mod=1000000007;
const int N=100005;
int n,x,y;
int a[N],b[N],c[N];
ll res=0x3f3f3f3f;
int X[N];
void dfs(int u){if(u==x+1){ll tmp=a[1];ll base=1;for(int i=2;i<=x;i++){base=base*X[i-1]%mod;tmp=(tmp+a[i]*base)%mod;}res=min(tmp,res);return ;}for(int i=2;i<=n;i++){if(i>=c[u]){X[u]=i; dfs(u+1);}}
}
signed main(){scanf("%d",&n);scanf("%d",&x);
for(int i=x;i>=1;i--)scanf("%d",&a[i]);scanf("%d",&y);for(int i=y;i>=1;i--)scanf("%d",&b[i]);
// 最小的差
// 既然A>=B ,那么x一定大于等于y
// 每一数位上的数 字要小于其进制for(int i=1;i<=x;i++){c[i]=max(a[i],b[i])+1;//进制大于等于c[i]a[i]=a[i]-b[i];if(c[i]<2)c[i]=2;}dfs(1);cout<<res;return 0;
}
贪心AC版
解释一
因为每一位进制都会 乘到 A 和 B里面,当 base 越大的时候 A 和 B都会越大,但是因为 A >= B 的,所以 A 的增长速率是始终大于 B 的, 所以 base越大,A - B 的差值就越大,所以我们只要每次取 base 最小,就能满足 A - B 的差值最小了,又因为每一位的值都是由前面每一位的进制乘起来的
解释二
借位思想,极限思维, 一旦碰到A[i]<B[i]A[i]<B[i]A[i]<B[i]就向高位借位,由于 A>=BA>=BA>=B,最后一定可以使得 每个位置都有A[i]>=B[i]A[i]>=B[i]A[i]>=B[i]
解释三
秦九韶算法
#include <bits/stdc++.h>
using namespace std;
#define ll long long int
const int mod=1000000007;
const int N=100005;
int n,x,y;
int a[N],b[N],c[N];
ll res=0;
signed main(){scanf("%d",&n);scanf("%d",&x);for(int i=x;i>=1;i--)scanf("%d",&a[i]);scanf("%d",&y);for(int i=y;i>=1;i--)scanf("%d",&b[i]);
// 最小的差
// 既然A>=B ,那么x一定大于等于y
// 每一数位上的数 字要小于其进制ll base=1;for(int i=1;i<=x;i++){c[i]=max(a[i],b[i])+1;//进制大于等于c[i]a[i]=a[i]-b[i];//不要改变了a[i]的含义又去用原a[i]的值 不要交换两句顺序if(c[i]<2)c[i]=2;res=(res+a[i]*base)%mod;base=base*c[i]%mod;}cout<<res;return 0;
}
相关文章:

第十三届蓝桥杯
这里写目录标题一、刷题统计(ceil函数返回的是等值于某最小整数的浮点值,不强制转换回int就wa,没错就连和int整数相加都wa二、修剪灌木(主要应看清楚会调转方向三、统计子矩阵(前缀和滑动窗口⭐)四、[积木画…...

消息队列mq
应用场景: 1、解耦 2、削峰填谷 3、异步处理 4、消息通讯 工作模式: 一个消息只能被消费一次(订阅模式除外),消费者接受到消息会回调业务逻辑,消费逻辑写在回调函数里面。 1、简单模式:一个生产…...
[学习笔记]黑马程序员Spark全套视频教程,4天spark3.2快速入门到精通,基于Python语言的spark教程
文章目录视频资料:一、Spark基础入门(环境搭建、入门概念)第二章:Spark环境搭建-Local2.1 课程服务器环境2.2 Local模式基本原理2.3 安装包下载2.4 Spark Local模式部署第三章:Spark环境搭建-StandAlone3.1 StandAlone…...

git push和 git pull的使用
git push与git pull是一对推送/拉取分支的git命令。git push 使用本地的对应分支来更新对应的远程分支。$ git push <远程主机名> <本地分支名>:<远程分支名>*注意: 命令中的本地分支是指将要被推送到远端的分支,而远程分支是指推送的目标分支&am…...

首发,pm3包,一个用于多组(3组)倾向评分匹配的R包
目前,本人写的第二个R包pm3包已经正式在CRAN上线,用于3组倾向评分匹配,只能3组不能多也不能少。 可以使用以下代码安装 install.packages("pm3")什么是倾向性评分匹配?倾向评分匹配(Propensity Score Match…...
基于Canal的数据同步
基于Canal的数据同步 一、 系统结构 该数据同步系统由Spring Boot和Canal共同组成。 Spring Boot 是一个流行的 Java Web 框架,而 Canal 则是阿里巴巴开源的 MySQL 数据库的数据变更监听框架。结合 Spring Boot 和 Canal,可以实现 MySQL 数据库的实时数…...
vuetify设置页面默认主题色
前言 最近工作中接到一个任务: 项目中分light和dark两种主题色a、b页面默认为dark其他页面默认为light 项目前端环境: vue2jsyarnvuexvuetifyelement ui 解决思路 routerjs中配置路径时进行默认主题设置 在左侧aside点击菜单时,进行主题切…...

【Python入门第二十三天】Python 继承
Python 继承 继承允许我们定义继承另一个类的所有方法和属性的类。 父类是继承的类,也称为基类。 子类是从另一个类继承的类,也称为派生类。 创建父类 任何类都可以是父类,因此语法与创建任何其他类相同: 实例 创建一个名为…...

C#中,读取一个或多个文件内容的方法
读取一个或多个文件内容的方法 在C#中,可以使用File.ReadAllLines方法一次读取多个文件中的所有行内容。例如,以下代码读取了两个文件中的所有行内容,然后将它们合并在一起: string[] file1Lines File.ReadAllLines("file1…...

1 基于神经辐射场(neural Radiance Fileds, Nerf)的三维重建- 简介
Nerf简介 Nerf(neural Radiance Fileds) 为2020年ICCV上提出的一个基于隐式表达的三维重建方法,使用2D的 Posed Imageds 来生成(表达)复杂的三维场景。现在越来越多的研究人员开始关注这个潜力巨大的领域,也…...
水果FLStudio21.0.0中文版全能数字音乐工作站DAW
FL Studio 21.0.0官方中文版重磅发布纯正简体中文支持,更快捷的音频剪辑及素材管理器,多样主题随心换!Mac版新增对苹果M2/1家族芯片原生支持。编曲、剪辑、录音、混音,20余年的技术积淀和实力研发,FL Studio 已经从电音…...

【GlobalMapper精品教程】055:GM坐标转换器的巧妙使用
GM软件提供了一个简单实用的坐标转换工具,可以实现地理坐标和投影坐标之间的高斯正反算及多种转换计算。 文章目录 一、坐标转换器认识二、坐标转换案例1. 地理坐标←→地理坐标2. 地理坐标←→投影坐标三、在输出坐标上创建新的点四、其他转换工具的使用一、坐标转换器认识 …...
函数是如何实现的)
C语言之中rand()函数是如何实现的
rand()函数是一个C标准库中的随机数生成函数,用于生成一个范围在0到RAND_MAX之间的伪随机数。RAND_MAX是一个常量,它是随机数的最大值,通常被定义为32767。 rand()函数的实现原理可以概括为以下几个步骤: 初始化随机数生成器 在…...
winform控件PropertyGrid的应用(使运行中的程序能像vistual studio那样设置控件属性)
上周在看别人写的上位机demo代码时,发现创建的项目模板是"Windows 窗体控件库"(如下图) 生成的项目结构像自定义控件库,没有程序入口方法Main,但却很神奇能调试,最后发现原来Vistual Studio启动了一个外挂程序UserContr…...

SBUS的协议详解
SBUS 1.串口配置: 100k波特率, 8位数据位(在stm32中要选择9位), 偶校验(EVEN), 2位停止位, 无控流,25个字节, 2.协议格式: [startbyte] [data1][data2]……...
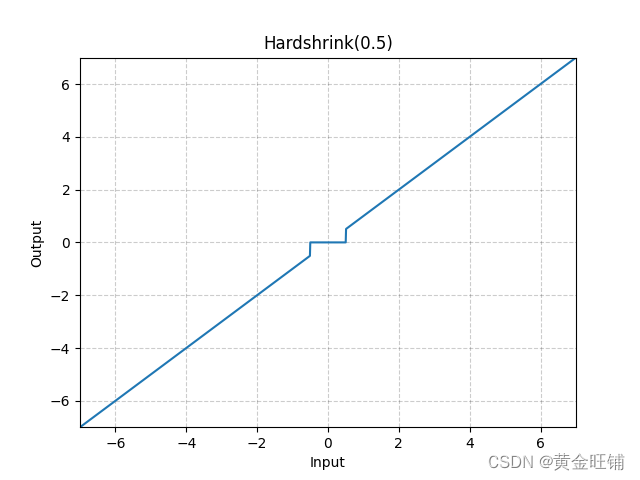
【PyTorch】教程:torch.nn.Hardshrink
torch.nn.Hardshrink CLASS torch.nn.Hardshrink(lambd0.5) 参数 lambd ([float]) – the λ\lambdaλ 默认为 0.5 定义 HardShrink(x){x,if x>λx,if x<−λ0,otherwise \text{HardShrink}(x) \begin{cases} x, & \text{ if } x > \lambda \\ x, & \text{…...

JavaScript 函数参数
JavaScript 函数对参数的值(arguments)没有进行任何的检查。JavaScript 函数参数与大多数其他语言的函数参数的区别在于:它不会关注有多少个参数被传递,不关注传递的参数的数据类型。函数显式参数与隐藏参数(arguments)在先前的教程中,我们已…...

【C】标准IO库函数
fopen/fclose #include <stdio.h>FILE *fopen(const char *path, const char *mode); 返回值:成功返回文件指针,出错返回NULL并设置errnoint fclose(FILE *fp); 返回值:成功返回0,出错返回EOF并设置errnomode参数是一个字符…...
http客户端Feign
Feign替代RestTemplate RestTemplate方式调用存在的缺陷 String url"http://userservice/user/"order.getUserId();User user restTemplate.getForObject(url, User.class); 代码可读性差,变成体验不统一; 参数复杂的时候URL难以维护。 &l…...

如何在Java中使用枚举类:从入门到进阶
枚举类是Java中一种特殊的数据类型,它允许我们将一组有限的值作为一组常量来使用,这些常量在代码中具有固定的名称和类型。在Java中,枚举类通常用于代表状态、选项和类别等具有离散值的变量。本篇博客将深入探讨Java中的枚举类,包…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
