数据结构学习 jz39 数组中出现次数超过一半的数字
关键词:排序 摩尔投票法
摩尔投票法没学过所以没有想到,其他的都自己想。
题目:库存管理 II

方法一:
思路:
排序然后取中间值。因为超过一半所以必定在中间值是我们要的结果。
复杂度计算:
时间复杂度O(nlogn)
空间复杂度O(1)
代码:
class Solution {
public:int inventoryManagement(vector<int>& stock) {if(stock.size()==1) return stock[0];sort(stock.begin(),stock.end());return stock[stock.size()/2];}
};方法二:
哈希表统计法。
思路:
哈希表统计一遍,如果结果大于一半就返回。
复杂度计算:
时间复杂度O(n)
空间复杂度O(k)数的总类
代码:
class Solution {
public:int inventoryManagement(vector<int>& stock) {if(stock.size()==1) return stock[0];unordered_map<int,int> hash;for(int i=0;i<stock.size();++i){hash[stock[i]]++;if(hash[stock[i]]>stock.size()/2) return stock[i];}return 0;}
};方法三:最佳解法
摩尔投票法。
思路:
我是看了k神的题解才会的。建议看。
复杂度计算:
时间复杂度O(n)
空间复杂度O(1)
代码:
class Solution {
public:int inventoryManagement(vector<int>& stock) {int x=0;int votes=0;for(const int&num:stock){if(votes==0) x=num;if(num==x) votes+=1;//和假设的众数x一样,就+1else votes+=-1;//不一样就-1}return x;}
};相关文章:

数据结构学习 jz39 数组中出现次数超过一半的数字
关键词:排序 摩尔投票法 摩尔投票法没学过所以没有想到,其他的都自己想。 题目:库存管理 II 方法一: 思路: 排序然后取中间值。因为超过一半所以必定在中间值是我们要的结果。 复杂度计算: 时间复杂度…...

基于Linux的Flappy bird游戏开发
项目介绍 主要是使用C语言实现,开启C项目之旅。 复习巩固C语言、培养做项目的思维。 功能: 按下空格键小鸟上升,不按下落; 显示小鸟需要穿过的管道; 小鸟自动向右飞行;(管道自动左移和创建&a…...

排序算法6---快速排序(非递归)(C)
回顾递归的快速排序,都是先找到key中间值,然后递归左区间,右区间。 那么是否可以实现非递归的快排呢?答案是对的,这里需要借助数据结构的栈。将右区间左区间压栈(后进先出),然后取出…...

【Verilog】期末复习——设计带异步清零且高电平有效的4位循环移位寄存器
系列文章 数值(整数,实数,字符串)与数据类型(wire、reg、mem、parameter) 运算符 数据流建模 行为级建模 结构化建模 组合电路的设计和时序电路的设计 有限状态机的定义和分类 期末复习——数字逻辑电路分…...

银行网络安全实战对抗体系建设实践
文章目录 前言一、传统攻防演练面临的瓶颈与挑战(一)银行成熟的网络安全防护体系1、缺少金融特色的演练场景设计2、资产测绘手段与防护体系不适配3、效果评价体系缺少演练过程维度相关指标 二、实战对抗体系建设的创新实践(一)建立…...

SwiftUI之深入解析Alignment Guides的超实用实战教程
一、Alignment Guide 简介 Alignment guides 是一个强大的布局工具,但通常未被充分利用。在很多情况下,它们可以帮助我们避免更复杂的选项,比如锚点偏好。如下所示,对对齐的更改也可以自动(并且容易地)动画…...

java获取视频文件的编解码器
java获取视频文件的编解码器 引入jar包: <dependency><groupId>org.bytedeco</groupId><artifactId>javacv-platform</artifactId><version>1.5.9</version></dependency>测试类 package com.jd.brand.approve.…...
)
动态规划Day06(完全背包)
完全背包 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。 完全背包和01背包问题唯一不同…...
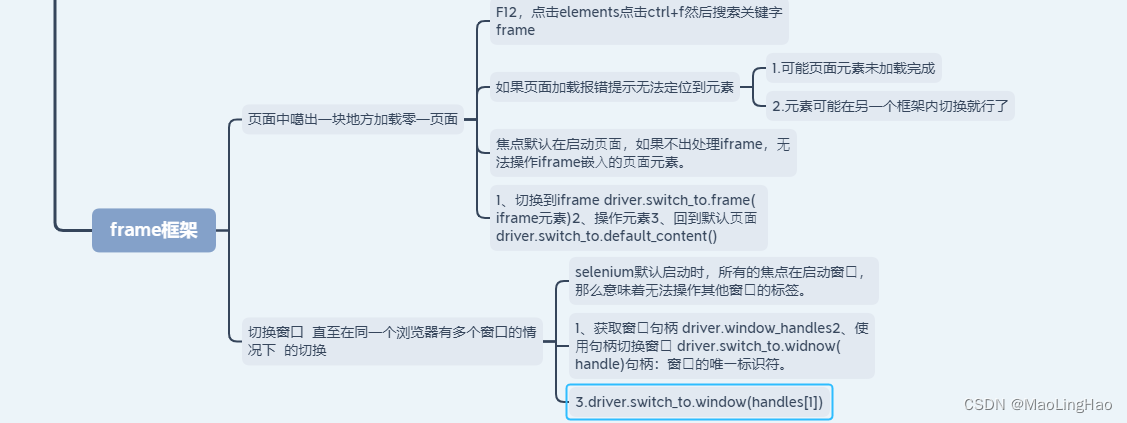
selenium之框架之窗口
...
)
华为OD机试 - 最小矩阵宽度(Java JS Python C)
题目描述 给定一个矩阵,包含 N * M 个整数,和一个包含 K 个整数的数组。 现在要求在这个矩阵中找一个宽度最小的子矩阵,要求子矩阵包含数组中所有的整数。 输入描述 第一行输入两个正整数 N,M,表示矩阵大小。 接下来 N 行 M 列表示矩阵内容。 下一行包含一个正整数 K…...

嵌入式linux_C应用学习之API函数
1.文件IO 1.1 open打开文件 #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> int open(const char *pathname, int flags); int open(const char *pathname, int flags, mode_t mode);pathname:字符串类型,用于标…...
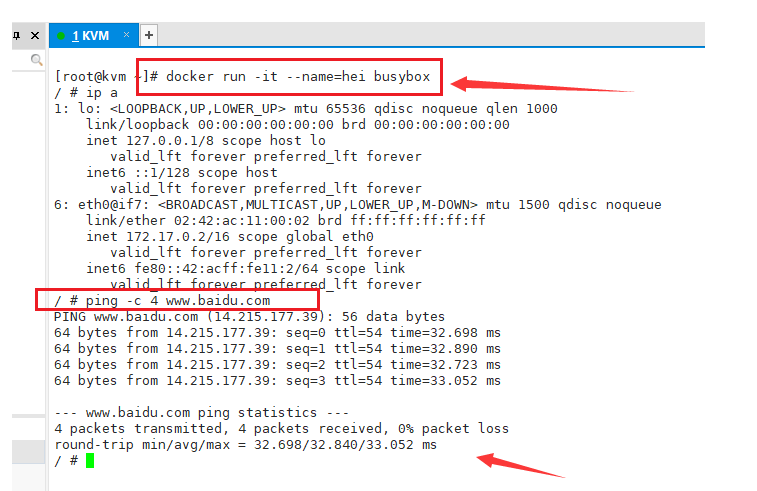
【ubuntu】docker中如何ping其他ip或外网
docker中如何ping其他ip或外网 示例图: 运行下面命令: docker run -it --namehei busybox看情况需要加权限 sudo,即: sudo docker run -it --namehei busyboxping 外网 ping -c 4 www.baidu.comping 内网 ping -c 4 192.168.…...

【Vue3+Ts项目】硅谷甄选 — 品牌管理+平台属性管理+SPU管理+SKU管理
一、品牌管理模块 1.1 静态模块搭建 使用到element-plus的card、button、table、pagination等组件:src/views/product/trademark/index.vue <template><el-card><!-- 卡片顶部添加品牌按钮 --><el-button type"primary" size&quo…...

计算机图形学流体模拟 blender 渲染脚本
做流体模拟的时候,想要复现别人的成果,但是别人的代码都是每帧输出 ply 格式的文件,渲染部分需要自己完成 看了一下,似乎用 blender 是最简单的,于是记录一下过程中用到的代码 Blender 版本 4.0 批量导入 ply 假设…...
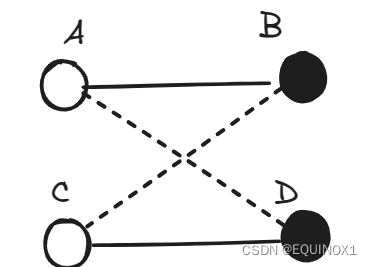
二分图带权最大匹配-KM算法详解
文章目录 零、前言一、红娘再牵线二、二分图带权最大完备匹配2.1二分图带权最大匹配2.2概念2.3KM算法2.3.1交错树2.3.2顶标2.3.3相等子图2.3.4算法原理2.3.5算法实现 三、OJ练习3.1奔小康赚大钱3.2Ants 零、前言 关于二分图:二分图及染色法判定-CSDN博客 关于二分…...

Redis命令 - Sets命令组常用命令
Set集合,无序,一堆不重复值的组合。利用redis提供的set数据结构,可以存储一些集合性的数据。 使用场景:例如,实现如共同关注、共同喜好、二度好友等 1、SADD key member [member …] 向集合中添加一个或者多个成员 …...

DA14531-外设驱动篇-I2C通信应用
文章目录 1.I2C通信应用相关文件2.宏定义列表3.主要函数接口4.应用代码实例1.I2C通信应用相关文件 1)i2c.c和i2c.h(SDK文件) 2)app_I2cProtocol.c和app_I2cProtocol.h(用户应用文件) 2.宏定义列表 宏定义注解I2C_ADDRESSING_7B7-bit 地址I2C_ADDRESSING_10B10-bit 地址…...

Git仓库管理笔记
问题: hint: the same ref. If you want to integrate the remote changes, use Done 解决: 解决方法: 1、先使用pull命令: git pull --rebase origin master 2、再使用push命令: git push -u origin master...
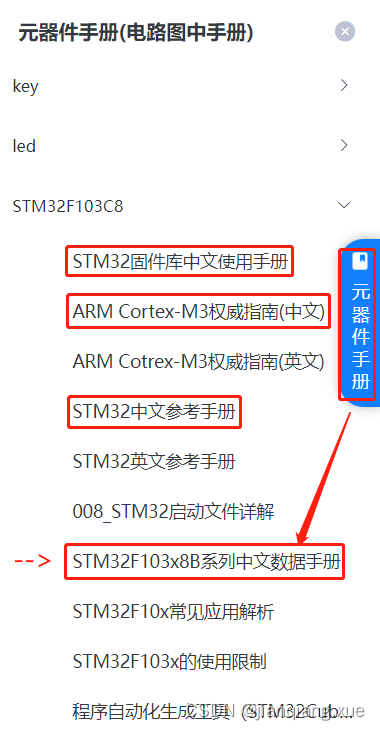
[嵌入式软件][入门篇] 搭建在线仿真平台(STM32)
文章目录 一、注册平台二、创建首个项目三、硬件介绍 一、注册平台 进入官方,进行注册: 在线仿真地址 二、创建首个项目 ① 新建项目 ② 搭建一个电路 ③ 用STM32F103搭建一个简单电路 ④ 进入编码界面 三、硬件介绍 红框是必看文档ÿ…...

设置5台SSH互免的虚拟机服务器配置
搭建一套集群虚拟机,往往都需要互免设置,过程很简单,避免以后再搭建还得网上搜索,我直接将这一个步骤写成笔记,记录下来,方便后续查阅。 步骤如下—— 1、准备五台机器 服务器名字服务器IPhadoop1192.16…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
