蓝桥杯 第三场 小白入门赛
召唤神坤
- 有意思🤔(ikun)。
- 虽然是第一题但也要配得上神坤的身份。
思路1
- 枚举分母,选择一个数据结构来选出分母两侧最大的两个数做分子。
- 2s常数大些也无碍。
- 我选择好写的ST表
思路2
- 写两个 d p dp dp 分别表示 1 1 1 到 i i i 的最大值, i i i 到 n n n 的最大值。再枚举。
- 这个不放码了看的别人的思路。
signed main() {int T = 1;
// T = read();while (T--) {int n = read();vector<int> a(n + 1), logn(n + 1);vector<vector<int>> f(n + 1, vector<int>(30));for (int i = 1; i <= n; ++i) f[i][0] = a[i] = read();logn[0] = -1;for (int i = 1; i <= n; ++i) logn[i] = logn[i >> 1] + 1;for (int j = 1; j <= logn[n]; ++j) {for (int i = 1; i + (1 << j) - 1 <= n; ++i) {f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);}}int ans = 0;for (int i = 2; i < n; ++i) {int l = 1, r = i - 1, s = logn[r - l + 1];int wi = max(f[l][s], f[r - (1 << s) + 1][s]);l = i + 1, r = n, s = logn[r - l + 1];int wk = max(f[l][s], f[r - (1 << s) + 1][s]);ans = max(ans, (wi + wk) / a[i]);}write(ans);}return 0;
}
聪明的交换策略
分析
- 依据题意就是要么 0 0 0 左 1 1 1 右,要么 1 1 1 左 0 0 0 右。
- 考虑 0 0 0 左还是 0 0 0 右即可。考虑 1 1 1 也行一样的。
signed main() {int T = 1;
// T = read();while (T--) {int n = read();string s; cin >> s;vector<int> pos;for (int i = 0; i < s.size(); ++i) {if (s[i] ^ '1') pos.push_back(i);}int ans = 1e17, tmp1 = 0, tmp2 = 0;for (int i = 0; i < pos.size(); ++i) tmp1 += pos[i] - i;ans = min(ans, tmp1);for (int i = pos.size() - 1, j = n - 1; i >= 0; --i, --j) tmp2 += j - pos[i];ans = min(ans, tmp2);write(ans);}return 0;
}
怪兽突击
ps:总觉得codeforces做过。。
思路
- 枚举每个 i i i (当然要小于等于 k k k )。
signed main() {int T = 1;
// T = read();while (T--) {int n = read(), k = read();vector<int> a(n + 1), b(n + 1);for (int i = 1; i <= n; ++i) a[i] = read();for (int i = 1; i <= n; ++i) b[i] = read();priority_queue<int, vector<int>, greater<int>> pq;int ans = 1e17, cnt = 0;for (int i = 1; i <= n && i <= k; ++i) {cnt += a[i];pq.push(a[i] + b[i]);ans = min(ans, cnt + (k - i) * pq.top());}write(ans);}return 0;
}
蓝桥快打
思路
- 根据 A , C A,C A,C 可以得出攻击次数的范围, B ≤ n ⋅ x B\leq n\cdot x B≤n⋅x 。
signed main() {int T = 1;T = read();while (T--) {int a = read(), b = read(), c = read();int r = a / c + (a % c > 0);writeln(b / r + (b % r > 0));}return 0;
}
奇怪的段
思路
- d p dp dp
- 方程: d p i = m a x ( d p i − 1 , j , d p i − 1 , j − 1 ) + a i ⋅ p j dp_i=max(dp_{i-1,j},dp_{i-1,j-1})+a_i\cdot p_j dpi=max(dpi−1,j,dpi−1,j−1)+ai⋅pj 。
- 注意有负数
signed main() {int T = 1;
// T = read();while (T--) {int n = read(), k = read();vector<int> a(n + 1), p(k + 1);vector<vector<int>> dp(n + 1, vector<int>(201, -1e15));dp[0][0] = 0;for (int i = 1; i <= n; ++i) a[i] = read();for (int i = 1; i <= k; ++i) p[i] = read();for (int i = 1; i <= n; ++i) {for (int j = 1; j <= k; ++j) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1]) + a[i] * p[j];}}write(dp[n][k]);}return 0;
}
小蓝的反击
ps:是个区间求解问题,涉及基础数论。
思路
- 枚举每一个 i i i ,找到最小位置 j j j 满足 A ∣ ∏ k = i j 1 a k , B ∣ ∏ k = i j 2 a k A| \prod_{k=i}^{j_1}a_k,\;B|\prod_{k=i}^{j_2}a_k A∣∏k=ij1ak,B∣∏k=ij2ak 。
- 如果 j 1 j_1 j1 不存在那么往后再也不能整除 A A A 了。如果 j 2 j_2 j2 不存在,那么从 j 1 j_1 j1 到 n n n 都能整出 A A A 。都存在只有 j 2 > j 1 j_2 >j_1 j2>j1 才对答案有贡献。
- 对 A , B A,B A,B 质因数分解记录因子和各因子数量。
- 对 A , B A,B A,B 每一个因子做前缀和。
- 二分枚举区间询问是否存在(该有的因子和数量都要满足)。
ps:前缀和那儿显然是个二维的,试想质因数分解有可能出现因数很大的情况,第二维是因数大小会 M E L MEL MEL ,所以第二维应该为数量,而数量最多是10(前十个质数相乘已经 > 1 0 9 >10^9 >109 )。看题解有个 d p dp dp 的,巨,我不会。
signed main() {auto getFactor = [&] (int v) {vector<pii> vec;for (int i = 2; i <= v / i; ++i) {if (!(v % i)) {vec.push_back({i, 0});while (!(v % i)) v /= i, ++vec.back().second;}}if (v ^ 1) vec.push_back({v, 1});return vec;};int T = 1;
// T = read();while (T--) {int n = read(), a = read(), b = read();auto vec1 = getFactor(a), vec2 = getFactor(b);vector<vector<int>> prefa(n + 1, vector<int>(10)), prefb(n + 1, vector<int>(10));for (int i = 1; i <= n; ++i) {int u = read();for (int j = 0; j < vec1.size(); ++j) {int tmp = u, v = vec1[j].first;while (!(tmp % v)) {++prefa[i][j];tmp /= v;}prefa[i][j] += prefa[i - 1][j];}for (int j = 0; j < vec2.size(); ++j) {int tmp = u, v = vec2[j].first;while (!(tmp % v)) {++prefb[i][j];tmp /= v;}prefb[i][j] += prefb[i - 1][j];}}auto find = [&] (int i, int j, int cnt, int op) {int l = i, r = n, tmp = op? prefb[i - 1][j]: prefa[i - 1][j];int ans = -1;while (l <= r) {int mid = (l + r) >> 1, v = op? prefb[mid][j]: prefa[mid][j];if (v - tmp >= cnt) ans = mid, r = mid - 1;else l = mid + 1;}return ans;};long long int ans = 0;for (int i = 1; i <= n; ++i) {int pos1 = i;for (int j = 0; j < vec1.size(); ++j) {int pos = find(i, j, vec1[j].second, 0);if (pos ^ -1) pos1 = max(pos1, pos);else {pos1 = -1;break;}}if (pos1 == -1) break;int pos2 = i;for (int j = 0; j < vec2.size(); ++j) {int pos = find(i, j, vec2[j].second, 1);if (pos ^ -1) pos2 = max(pos2, pos);else {pos2 = -1;break;}}if (pos2 == -1) ans += (n - pos1 + 1) * 1ll;else if (pos2 > pos1) ans += (pos2 - pos1) * 1ll;}// write(ans);cout << ans;}return 0;
}
相关文章:

蓝桥杯 第三场 小白入门赛
召唤神坤 有意思🤔(ikun)。虽然是第一题但也要配得上神坤的身份。 思路1 枚举分母,选择一个数据结构来选出分母两侧最大的两个数做分子。2s常数大些也无碍。我选择好写的ST表 思路2 写两个 d p dp dp 分别表示 1 1 1 到 i…...
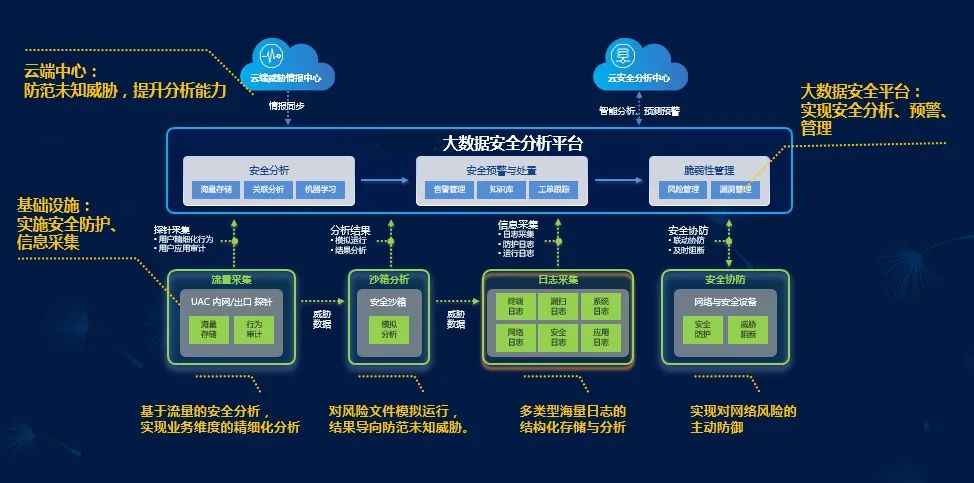
网络安全等级保护测评规划与设计
笔者单位网络结构日益复杂,应用不断增多,使信息系统面临更多的风险。同时,网络攻防技术发展迅速,攻击的技术门槛随着自动化攻击工具的应用也在不断降低,勒索病毒等未知威胁也开始泛滥。基于此,笔者单位拟进…...

Error: Cannot find module ‘vue-template-compiler‘ 问题解决
启动Vuepress项目时报了如下错误:Error: Cannot find module vue-template-compiler Error: Cannot find module vue-template-compiler Require stack: - /usr/local/lib/node_modules/vuepress/node_modules/vue-loader/lib/compiler.js - /usr/local/lib/node_…...
--练习题)
华为认证云计算专家(HCIE-Cloud Computing)--练习题
华为认证云计算专家(HCIE-Cloud Computing)–练习题 1.(判断题)华为云stack支持鲲鹏架构,业务可从X86过渡到鲲鹏。 正确答案:正确 2.(判断题)业务上云以后,安全方面由云服务商负责,客户自己不需要做任何防…...
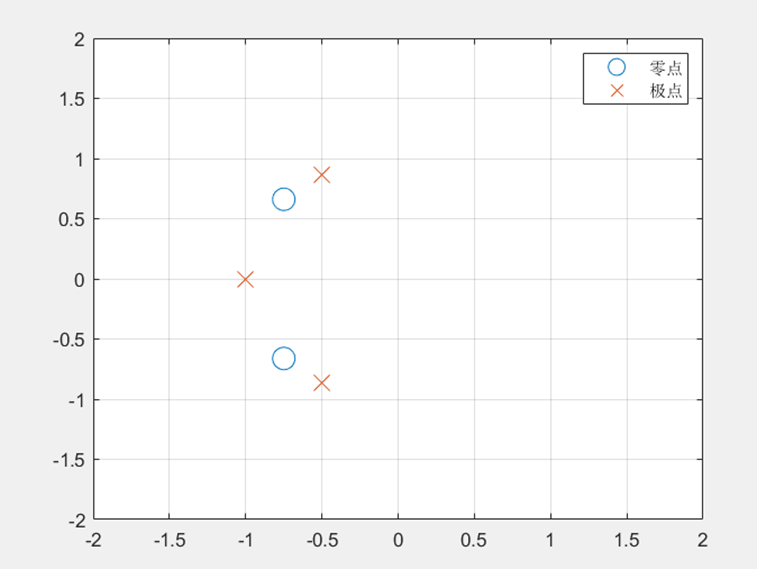
【MATLAB】【数字信号处理】产生系统的单位冲激响应h(t)与H(z)零极点分布
一、实验目的与要求 产生h(t) 与H(z) 零极点分布 二、实验仪器 微机,仿真软件MATLAB 2022a 三、实验内容与测试结果 1.已知描述连续系统的微分方程为y(t)5y(t)6y(t)2x(t)8x(t) ,计算系统的单位冲激响应h(t) 程序如下: clear all; ts0;…...

实验五:动态路由配置
实验五:动态路由配置 1.RIP 配置 【实验名称】 RIP 路由协议配置 【实验目的】掌握路由器 RIP 路由协议的基本配置 【实验设备】路由器( 2 台)、计算机( 2 台)、配置电缆( 1 根)、 V…...
苍穹外卖学习----出错记录
1.微信开发者工具遇到的问题: 1.1appid消失报错: {errMsg: login:fail 系统错误,错误码:41002,appid missing [20240112 16:44:02][undefined]} 1.2解决方式: appid可在微信开发者官网 登录账号后在开发栏 找到 复制后按以下步骤粘贴即…...
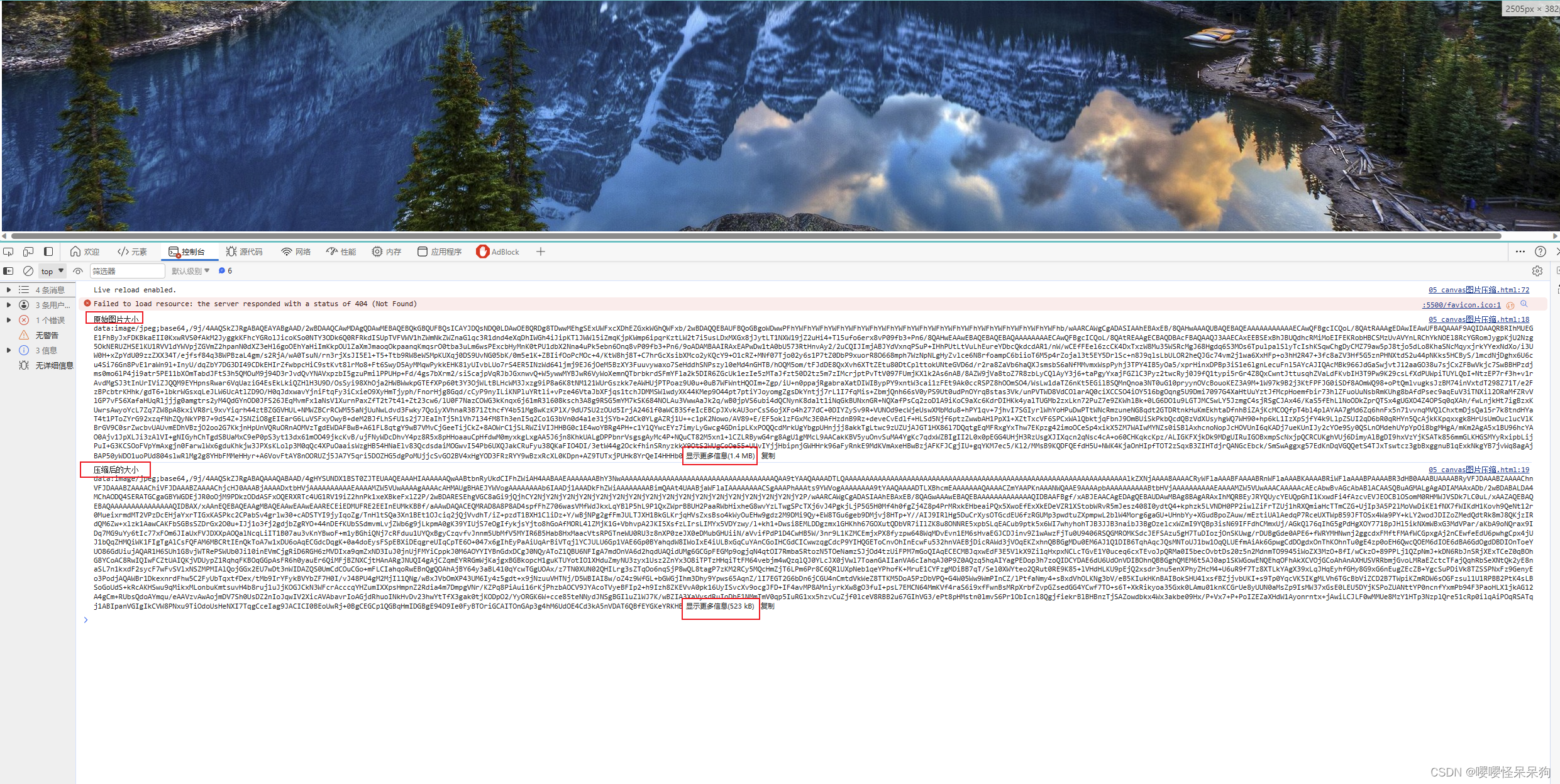
如何实现图片压缩
文章目录 1、canvas实现图片压缩2、其他 1、canvas实现图片压缩 canvas 实现图片压缩,主要是使用 canvas 的drawImage 方法 具体思路 拿到用户上传的文件转成base64创建一个 Image,主要是获取到这个图片的宽度和高度创建一个 2D 的画布,画布…...

机器学习算法实战案例:时间序列数据最全的预处理方法总结
文章目录 1 缺失值处理1.1 统计缺失值1.2 删除缺失值1.3 指定值填充1.4 均值/中位数/众数填充1.5 前后项填充 2 异常值处理2.1 3σ原则分析2.2 箱型图分析 3 重复值处理3.1 重复值计数3.2 drop_duplicates重复值处理 3 数据归一化/标准化3.1 0-1标准化3.2 Z-score标准化 技术交…...
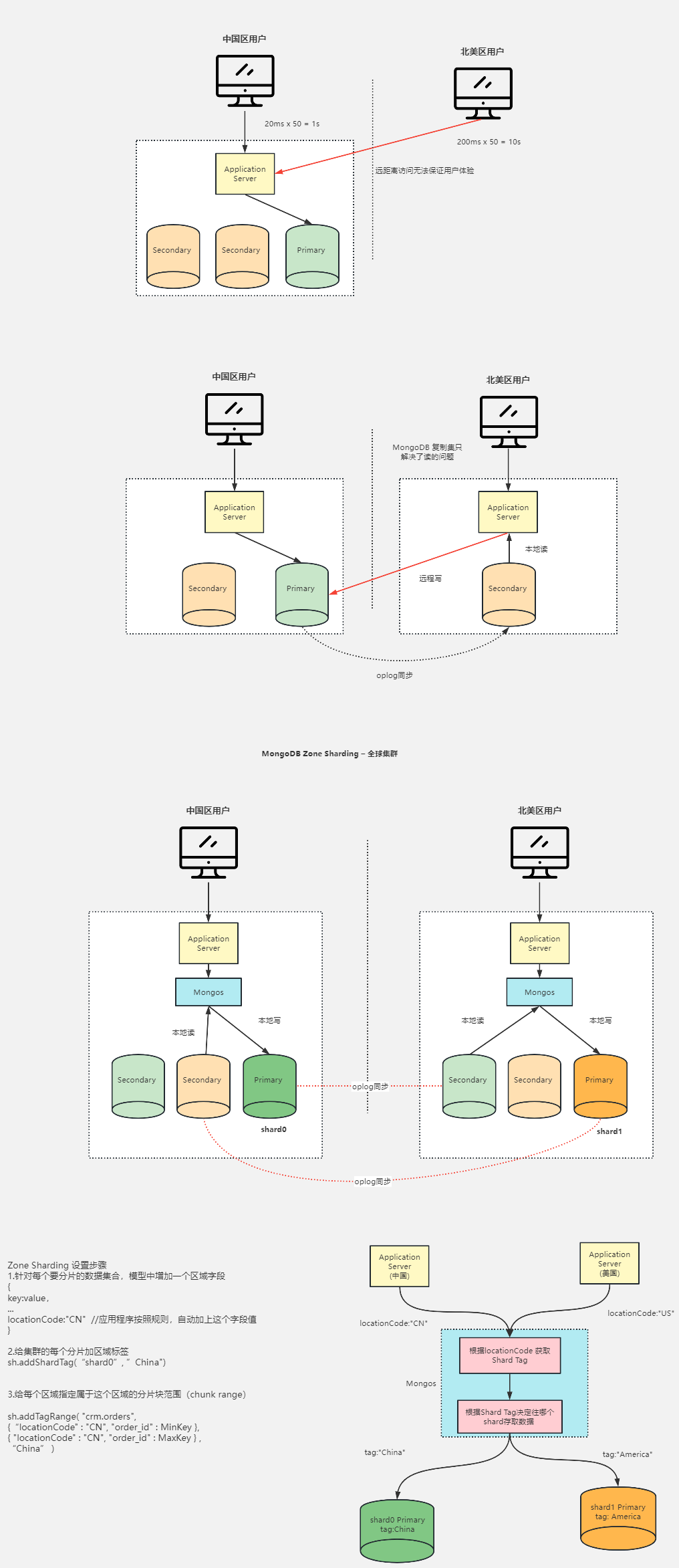
MongoDB高级集群架构设计
两地三中心集群架构设计 容灾级别 RPO & RTO RPO(Recovery Point Objective):即数据恢复点目标,主要指的是业务系统所能容忍的数据丢失量。RTO(Recovery Time Objective):即恢复时间目标&…...

C++中JSON与string格式互转
1、JSON-》string 操作步骤: 1、在C中新建一个json对象并赋值,然后将其转给char *data。 2、在使用 #include <json.h> 头文件时,通常是使用第三方库 jsoncpp。由于它不是标准库的一部分,所以需要从官网http://jsoncpp.sou…...

2023一带一路暨金砖国家技能发展与技术创新大赛 【企业信息系统安全赛项】国内赛竞赛样题
2023一带一路暨金砖国家技能发展与技术创新大赛 【企业信息系统安全赛项】国内赛竞赛样题 2023一带一路暨金砖国家技能发展与技术创新大赛 【企业信息系统安全赛项】国内赛竞赛样题第一阶段: CTF 夺旗项目1. CTF 夺旗任务一 命令注入任务二 SQL 注入 项目2. 序列化漏…...

【BBuf的CUDA笔记】十二,LayerNorm/RMSNorm的重计算实现
带注释版本的实现被写到了这里:https://github.com/BBuf/how-to-optim-algorithm-in-cuda/tree/master/apex 由于有很多个人理解,读者可配合当前文章谨慎理解。 0x0. 背景 我也是偶然在知乎的一个问题下看到这个问题,大概就是说在使用apex的…...
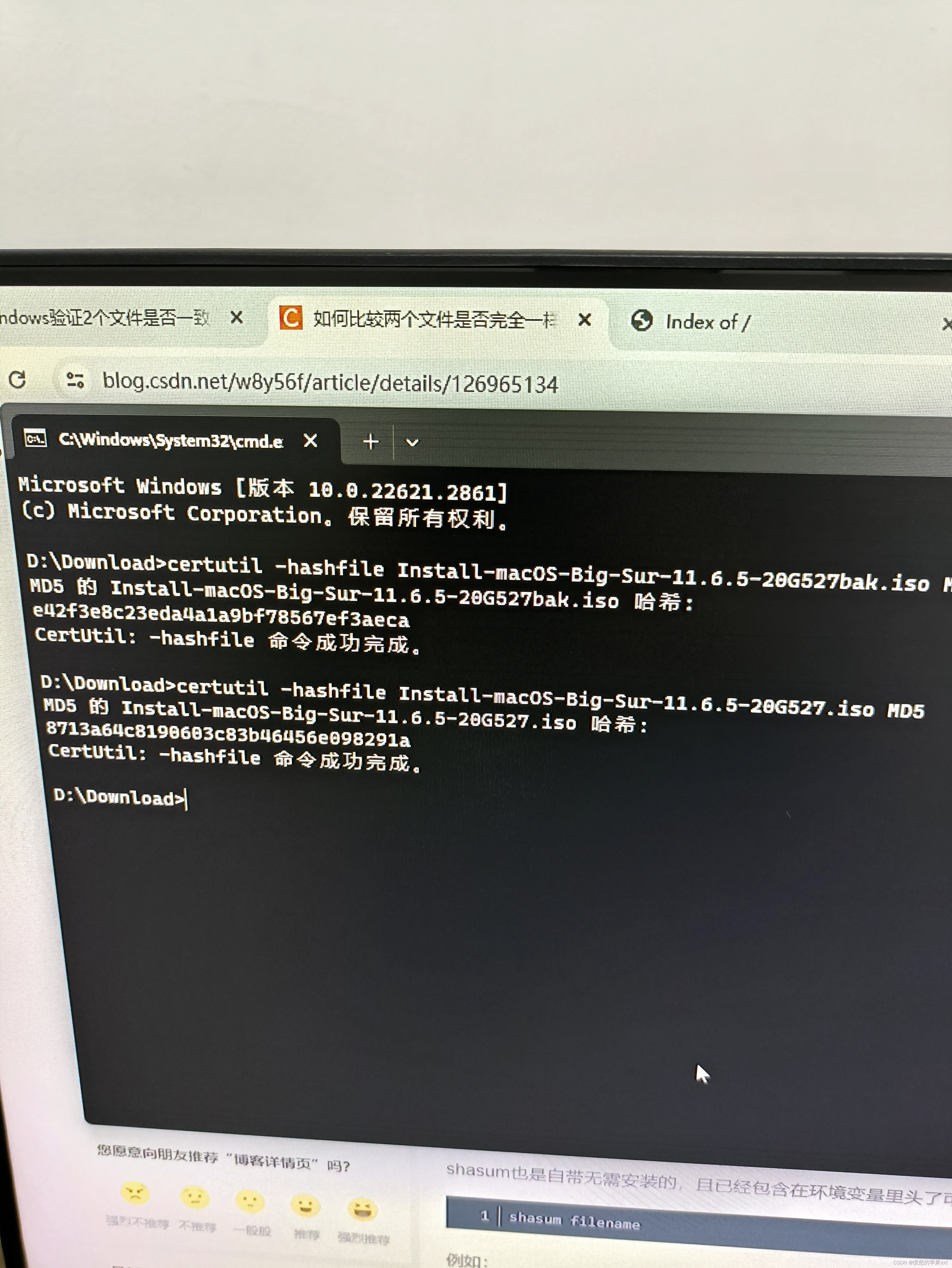
安装Mac提示安装无法继续,因为安装器已损坏
目录 事件起因报错原因 事件起因 有两台电脑,由于电脑1下载镜像文件很快,于是我先用电脑1下载这个大文件,然后安装openresty,电脑2用http链接下载这个大文件。电脑2安装中途就报安装无法继续,因为安装器已损坏。 报错原因 不知…...

脚本编程游戏引擎会遇到哪些问题
在游戏开发中,脚本编程已经成为了一种非常常见的方式,用来实现游戏逻辑和功能。但是脚本编程游戏引擎也可能会面临一些挑战和问题。下面简单的探讨一下都会遇到哪些问题,并且该如果做。 性能问题 脚本语言通常需要运行时解释执行࿰…...
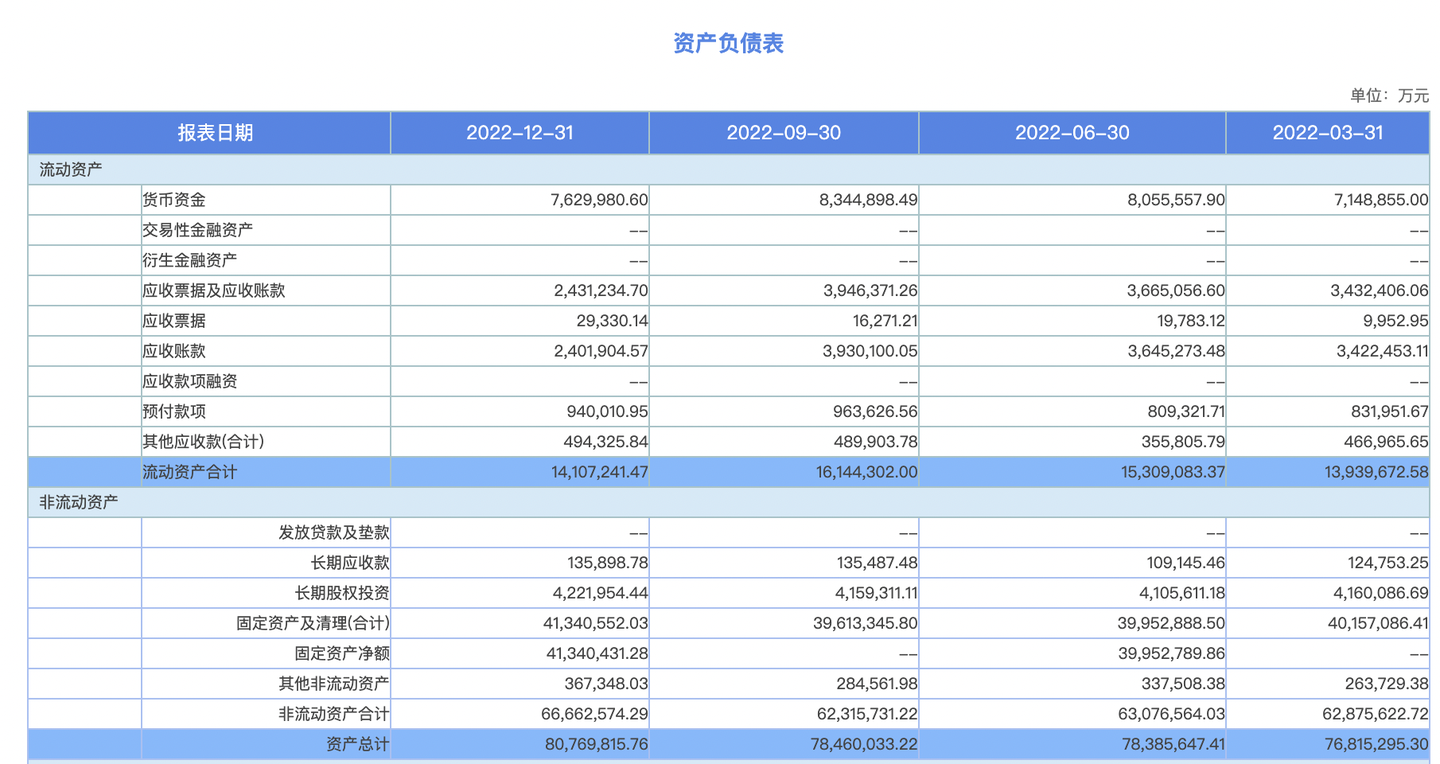
什么软件可以做报表?
数据报表,是商业领域中不可或缺的一部分,它通过表格、图表等形式,将复杂的数据进行整理、分析并呈现出来,帮助用户更好地理解数据的趋势和关系。数据报表不仅展示了业务现状和趋势,还支持多种数据分析和挖掘功能&#…...

数据结构学习 jz39 数组中出现次数超过一半的数字
关键词:排序 摩尔投票法 摩尔投票法没学过所以没有想到,其他的都自己想。 题目:库存管理 II 方法一: 思路: 排序然后取中间值。因为超过一半所以必定在中间值是我们要的结果。 复杂度计算: 时间复杂度…...

基于Linux的Flappy bird游戏开发
项目介绍 主要是使用C语言实现,开启C项目之旅。 复习巩固C语言、培养做项目的思维。 功能: 按下空格键小鸟上升,不按下落; 显示小鸟需要穿过的管道; 小鸟自动向右飞行;(管道自动左移和创建&a…...

排序算法6---快速排序(非递归)(C)
回顾递归的快速排序,都是先找到key中间值,然后递归左区间,右区间。 那么是否可以实现非递归的快排呢?答案是对的,这里需要借助数据结构的栈。将右区间左区间压栈(后进先出),然后取出…...

【Verilog】期末复习——设计带异步清零且高电平有效的4位循环移位寄存器
系列文章 数值(整数,实数,字符串)与数据类型(wire、reg、mem、parameter) 运算符 数据流建模 行为级建模 结构化建模 组合电路的设计和时序电路的设计 有限状态机的定义和分类 期末复习——数字逻辑电路分…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
