二分查找与搜索树的高频问题(算法村第九关白银挑战)
基于二分查找的拓展问题
山峰数组的封顶索引
852. 山脉数组的峰顶索引 - 力扣(LeetCode)
给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
提示:
3 <= arr.length <= 1050 <= arr[i] <= 106- 题目数据保证
arr是一个山脉数组
二分查找
public int peakIndexInMountainArray(int[] arr)
{int low = 1; //mid - 1 >= 0int high = arr.length - 2; // mid + 1 <= arr.length - 1while (low <= high){int mid = low + (high - low >> 1);//找到山峰if(arr[mid] > arr[mid - 1] && arr[mid] > arr[mid + 1])return mid;//山峰左侧(递增)else if(arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1])low = mid + 1;//山峰右侧(递减)elsehigh = mid - 1;}return -1;
}
旋转排序数组的最小值
无重复元素
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
二分查找


nums [pivot] >= nums [high] 时,移动 low

public int findMin(int[] nums){int left = 0;int right = nums.length - 1;while (left < right) // left == right 时找到最低点(最小值){int mid = left + (right - left >> 1);if(nums[mid] < nums[right])right = mid; //让 right 去触碰最低点(因为无法确定mid是不是最低点下标,故不能跳过它。如果是比较数值,那可以直接跳过,即 right = mid + 1)elseleft = mid + 1; // left 迫近最低点,与 right 汇合}return nums[left]; //left == right == mid}
有重复元素
154. 寻找旋转排序数组中的最小值 II - 力扣(LeetCode)
二分查找
重复元素要一个个排除
public int findMin(int[] nums){int left = 0;int right = nums.length - 1;while (left < right) // left == right 时找到最低点(最小值){int mid = left + (right - left >> 1);if(nums[mid] < nums[right])right = mid; //让 right 去触碰最低点else if(nums[mid] > nums[right])left = mid + 1; // left 迫近最低点,与 right 汇合elseright--; //处理重复元素要一步一步来}return nums[left]; //left == right == mid}
缺失的数字
剑指 offer :一个长度为 n - 1 的递增排序数组中的所有数字都是唯一的,每个数字的范围都是 [0,n-1] 。在范围 0~n-1 内的 n 个数字中有且只有一个数字不在该数组中,请找出这个数字。
LCR 173. 点名 - 力扣(LeetCode)
某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席,请返回他的学号。
示例 1:
输入: records = [0,1,2,3,5]
输出: 4
示例 2:
输入: records = [0, 1, 2, 3, 4, 5, 6, 8]
输出: 7
提示:
1 <= records.length <= 10000
二分查找
public static int missingNumber(int[] nums)
{int left = 0;int right = nums.length - 1;while (left <= right){int mid = left + (right - left >> 1);if (nums[mid] == mid)left = mid + 1; //让 left 去触碰缺失的元素,碰到后就不动了,交给 right 结束循环elseright = mid - 1;}return left;
}public static void main(String[] args)
{// n = 3 个数字, 数组长度(元素个数)为 n - 1 = 2, 元素范围 [0,2]int[] nums = {0, 1};System.out.println(missingNumber(nums)); // 输出 2// n = 7 个数字, 数组长度(元素个数)为 n - 1 = 6, 元素范围 [0,6]int[] nums2 = {0, 1, 2, 3, 5, 6};System.out.println(missingNumber(nums2)); // 输出 4
}
x 的平方根
LCR 072. x 的平方根 - 力扣(LeetCode)
给定一个非负整数 x ,计算并返回 x 的平方根,即实现 int sqrt(int x) 函数。
正数的平方根有两个,只输出其中的正数平方根。
如果平方根不是整数,输出只保留整数的部分,小数部分将被舍去。
示例 1:
输入: x = 4
输出: 2
示例 2:
输入: x = 8
输出: 2
解释: 8 的平方根是 2.82842...,由于小数部分将被舍去,所以返回 2
提示:
0 <= x <= 231 - 1
二分查找实现
public int mySqrt(int x)
{int left = 1;int right = x;int ans = 0;while (left <= right){int mid = left + (right - left >> 1);if(x / mid >= mid) //x >= mid²{ans = mid; //向下取整逼近答案left = mid + 1;}elseright = mid - 1;}return ans;
}
更多题目
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
875. 爱吃香蕉的珂珂 - 力扣(LeetCode)
29. 两数相除 - 力扣(LeetCode)
中序遍历与搜索树
简单来说,如果一棵二叉树是搜索树,则中序遍历序列是一个递增序列。
比较规范的定义是:
- 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
它的左、右子树也分别为二叉排序树。
下面两棵树的中序序列分别是{3,6,9,10,14,16,19},{3,6,9,10},因此都是搜索树。

二叉搜索树中的搜索
700. 二叉搜索树中的搜索 - 力扣(LeetCode)
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:
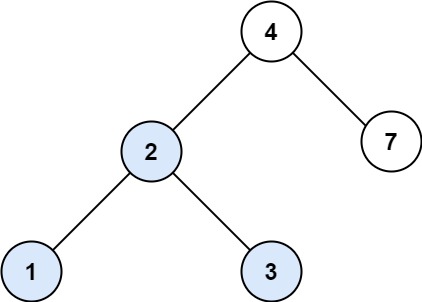
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
示例 2:
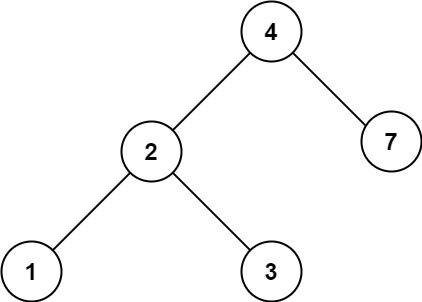
输入:root = [4,2,7,1,3], val = 5
输出:[]
递归
public TreeNode searchBST(TreeNode root, int val)
{if (root == null || root.val == val)return root;if (val < root.val) //进入左子树搜索return searchBST(root.left, val);else //否则进入右子树搜索return searchBST(root.right, val);
}
迭代
public TreeNode searchBST(TreeNode root, int val)
{while (root != null){if (root.val == val)break;else if (val < root.val)root = root.left;elseroot = root.right;}return root;
}
验证二叉搜索树
98. 验证二叉搜索树 - 力扣(LeetCode)
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
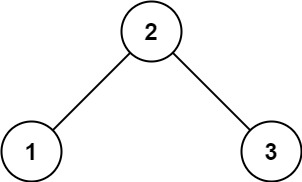
输入:root = [2,1,3]
输出:true
示例 2:
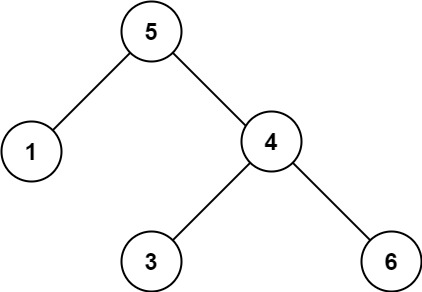
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在
[1, 104]内 -231 <= Node.val <= 231 - 1
中序遍历+实时检查
二叉搜索树「中序遍历」序列是升序的,所以我们在中序遍历时,实时检查当前节点的值是否大于前一个节点的值即可。
long pre = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root)
{if (root == null)return true;//检查左子树是否为二叉搜索树if(!isValidBST(root.left)) //等待左子树的返回结果。如果左子树下某个元素不满足要求,则退出所有递归return false;//检查当前节点是否大于等于前一个节点if (root.val <= pre)return false;pre = root.val;//检查右子树是否为二叉搜索树return isValidBST(root.right); //等待右子树的返回结果
}
中序遍历+是否升序
public boolean isValidBST(TreeNode root)
{ArrayList<Integer> res = new ArrayList<>();inOrder(root,res);for (int i = 1; i < res.size(); i++)if (res.get(i - 1) >= res.get(i))return false;return true;
}public void inOrder(TreeNode root, ArrayList<Integer> res)
{if (root == null)return;inOrder(root.left, res);res.add(root.val);inOrder(root.right, res);
}
更多题目
530. 二叉搜索树的最小绝对差 - 力扣(LeetCode)
501. 二叉搜索树中的众数 - 力扣(LeetCode)
相关文章:

二分查找与搜索树的高频问题(算法村第九关白银挑战)
基于二分查找的拓展问题 山峰数组的封顶索引 852. 山脉数组的峰顶索引 - 力扣(LeetCode) 给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i 1] > ... > arr[arr.length - 1…...

Python爬虫快速入门
Python 爬虫Sutdy 1.基本类库 request(请求) 引入 from urllib import request定义url路径 url"http://www.baidu.com"进行请求,返回一个响应对象response responserequest.urlopen(url)读取响应体read()以字节形式打印网页源码 response.read()转码 编码 文本–by…...
部署MinIO
一、安装部署MINIO 1.1 下载 wget https://dl.min.io/server/minio/release/linux-arm64/minio chmod x minio mv minio /usr/local/bin/ # 控制台启动可参考如下命令, 守护进程启动请看下一个代码块 # ./minio server /data /data --console-address ":9001"1.2 配…...
RK3566环境搭建
环境:vmware16,ubuntu 18.04 安装依赖库: sudo apt-get install repo git ssh make gcc libssl-dev liblz4-tool expect g patchelf chrpath gawk texinfo chrpath diffstat binfmt-support qemu-user-static live-build bison flex fakero…...
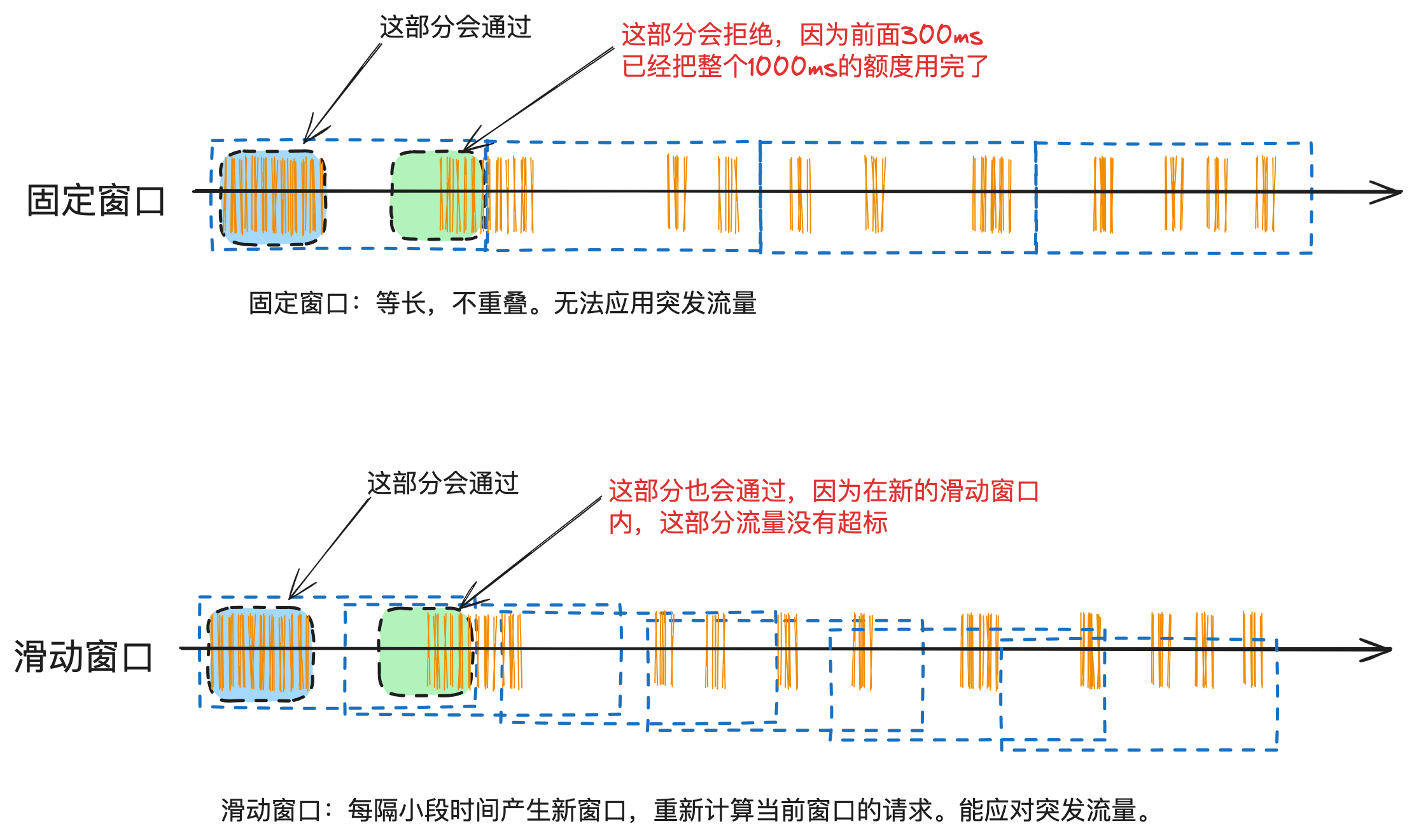
精确掌控并发:滑动时间窗口算法在分布式环境下并发流量控制的设计与实现
这是《百图解码支付系统设计与实现》专栏系列文章中的第(15)篇,也是流量控制系列的第(2)篇。点击上方关注,深入了解支付系统的方方面面。 上一篇介绍了固定时间窗口算法在支付渠道限流的应用以及使用redis…...

Python展示 RGB立方体的二维切面视图
代码实现 import numpy as np import matplotlib.pyplot as plt# 生成 24-bit 全彩 RGB 立方体 def generate_rgb_cube():# 初始化一个 256x256x256 的三维数组rgb_cube np.zeros((256, 256, 256, 3), dtypenp.uint8)# 填充立方体for r in range(256):for g in range(256):fo…...

03 顺序表
目录 线性表顺序表练习 线性表(Linear list)是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串。。。 线性表在逻辑上时线性结构,是连续的一条直线。但在物理结…...

2023年全球软件开发大会(QCon北京站2023)9月:核心内容与学习收获(附大会核心PPT下载)
随着科技的飞速发展,全球软件开发大会(QCon)作为行业领先的技术盛会,为世界各地的专业人士提供了交流与学习的平台。本次大会汇集了全球的软件开发者、架构师、项目经理等,共同探讨软件开发的最新趋势、技术与实践。本…...

ChatGPT 和 文心一言 的优缺点及需求和使用场景
ChatGPT和文心一言是两种不同的自然语言生成模型,它们有各自的优点和缺点。 ChatGPT(Generative Pre-trained Transformer)是由OpenAI开发的生成式AI模型,它在庞大的文本数据集上进行了预训练,并可以根据输入生成具有上…...
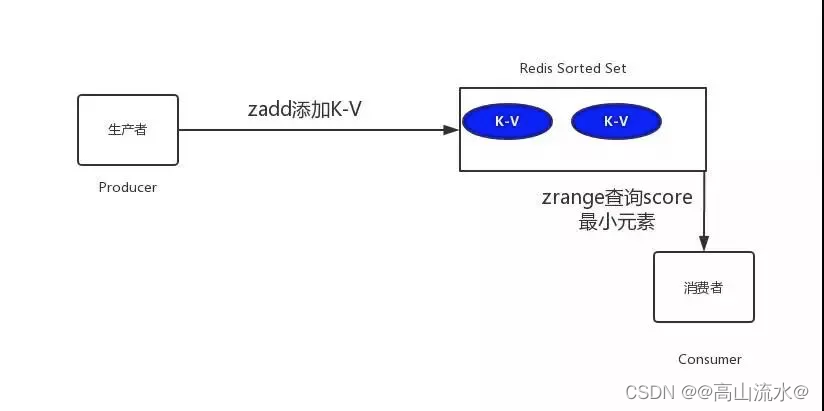
架构师之超时未支付的订单进行取消操作的几种解决方案
今天给大家上一盘硬菜,并且是支付中非常重要的一个技术解决方案,有这块业务的同学注意自己尝试一把哈! 一、需求如下: 生成订单30分钟未支付,自动取消 生成订单60秒后,给用户发短信 对上述的需求,我们给…...
【容器固化】 OS技术之OpenStack容器固化的实现原理及操作
1. Docker简介 要学习容器固化,那么必须要先了解下Docker容器技术。Docker是基于GO语言实现的云开源项目,通过对应用软件的封装、分发、部署、运行等生命周期的管理,达到应用组件级别的“一次封装,到处运行”。这里的应用软件&am…...

设置 SSH 通过密钥登录
我们一般使用 PuTTY 等 SSH 客户端来远程管理 Linux 服务器。但是,一般的密码方式登录,容易有密码被暴力破解的问题。所以,一般我们会将 SSH 的端口设置为默认的 22 以外的端口,或者禁用 root 账户登录。其实,有一个更…...

1.6 面试经典150题 - 买卖股票的最佳时机
买卖股票的最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易…...
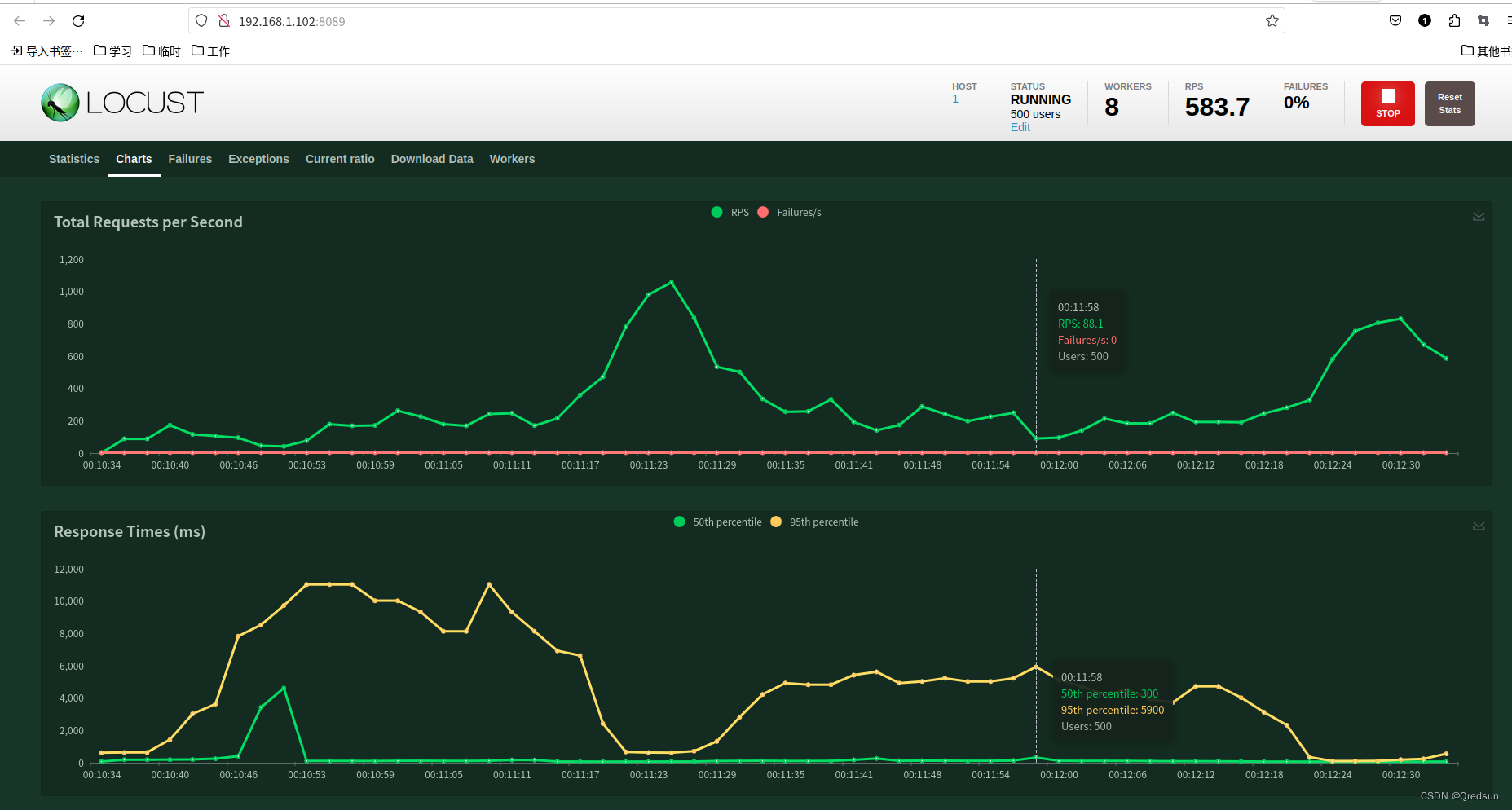
locust快速入门--使用分布式提高测试压力
背景: 使用默认的locust启动命令进行压测时,尽管已经将用户数设置大比较大(400),但是压测的时候RPS一直在100左右。需要增加压测的压力。 问题原因: 如果你是通过命令行启动的或者参考之前文章的启动方式…...
Pod资源——pod亲和性与反亲和性,pod重启策略)
K8s(三)Pod资源——pod亲和性与反亲和性,pod重启策略
目录 pod亲和性与反亲和性 pod亲和性 pod反亲和性 pod状态与重启策略 pod状态 pod重启策略 本文主要介绍了pod资源与pod相关的亲和性,以及pod的重启策略 pod亲和性与反亲和性 pod亲和性(podAffinity)有两种 1.podaffinity,…...

免费的域名要不要?
前言 eu.org的免费域名相比于其他免费域名注册服务,eu.org的域名后缀更加独特。同时,eu.org的域名注册也比较简单,只需要填写一些基本信息,就可以获得自己的免费域名。 博客地址 免费的域名要不要?-雪饼前言 eu.org…...

高通sm7250与765G芯片是什么关系?(一百八十一)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...
[Python进阶] Python操作MySQL数据库:pymysql
7.7 操作MySQL数据库:pymysql 7.7.1 准备工作(创建mysql数据库) PHPStudy介绍: phpstudy是一款非常有用的PHP开发工具,旨在帮助开发者更加便捷地进行PHP程序的开发与调试。它提供了一个友好的图形用户界面,使得用户能够方便地进…...
)
Vue3实现带点击外部关闭对应弹出框(可共用一个变量)
首先,假设您在单文件组件(SFC)中使用了Vue3,并且有两个div元素分别通过v-if和v-else来切换显示一个带有.elpopver类的弹出组件。在这种情况下,每个弹出组件应当拥有独立的状态管理(例如:各自的isOpen变量)。…...
)
可视化试题(一)
1. 从可视化系统设计的角度出发,通常需要根据系统将要完成的任务的类型选择交互技术。按照任务类型分类可以将数据可视化中的交互技术分为选择、( 重新配置 )、重新编码、导航、关联、( 过滤 )、概览和细节等八…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
