leetcode:最接近的三数之和---(双指针,排序,数组)
题目:
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
示例:
示例 1:
输入:nums = [-1,2,1,-4], target = 1 输出:2 解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
示例 2:
输入:nums = [0,0,0], target = 1 输出:0
提示:
3 <= nums.length <= 1000
-1000 <= nums[i] <= 1000
-104 <= target <= 104
代码:
class Solution {public int threeSumClosest(int[] nums, int target) {Arrays.sort(nums);int a,b,c;int res=Integer.MAX_VALUE;//target<=10000int sum=0;for(int i=0;i<nums.length;i++){//枚举a,//b,c 双指针a=i;b=i+1;c=nums.length-1;while(b<c){sum=nums[a]+nums[b]+nums[c];if(Math.abs(sum-target)<Math.abs(res-target)){res=sum;}if(sum>target){c--;}else if(sum<target){b++;}else{return target;}}}return res;}
}
运行结果:
相关文章:

leetcode:最接近的三数之和---(双指针,排序,数组)
题目: 给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。 返回这三个数的和。 假定每组输入只存在恰好一个解。 示例: 示例 1: 输入:nums [-1…...
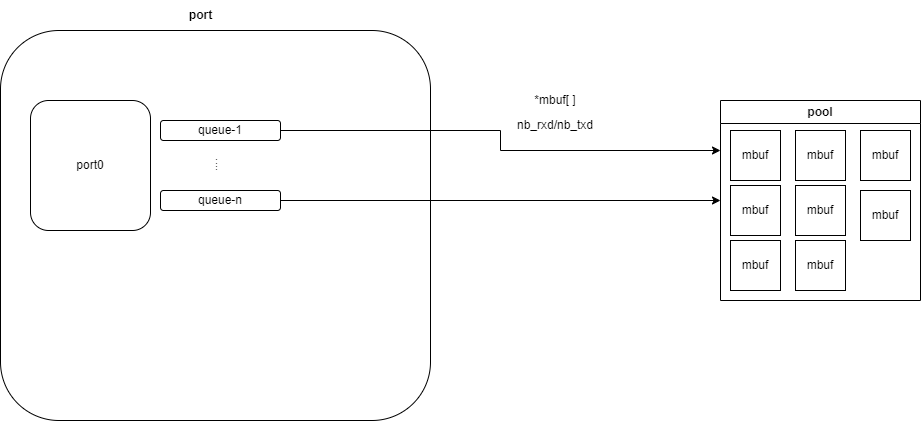
dpdk网络转发环境的搭建
文章目录 前言ip命令的使用配置dpdk-basicfwd需要的网络结构测试dpdk-basicfwddpdk-basicfwd代码分析附录basicfwd在tcp转发时的失败抓包信息DPDK的相关设置 前言 上手dpdk有两难。其一为环境搭建。被绑定之后的网卡没有IP,我如何给它发送数据呢?当然&a…...
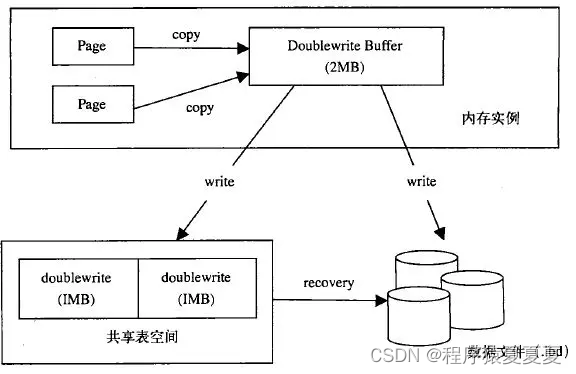
【MYSQL】存储引擎MyISAM和InnoDB
MYSQL 存储引擎 查看MySQL提供所有的存储引擎 mysql> show engines; mysql常用引擎包括:MYISAM、Innodb、Memory、MERGE 1、MYISAM:全表锁,拥有较高的执行速度,不支持事务,不支持外键,并发性能差&#x…...
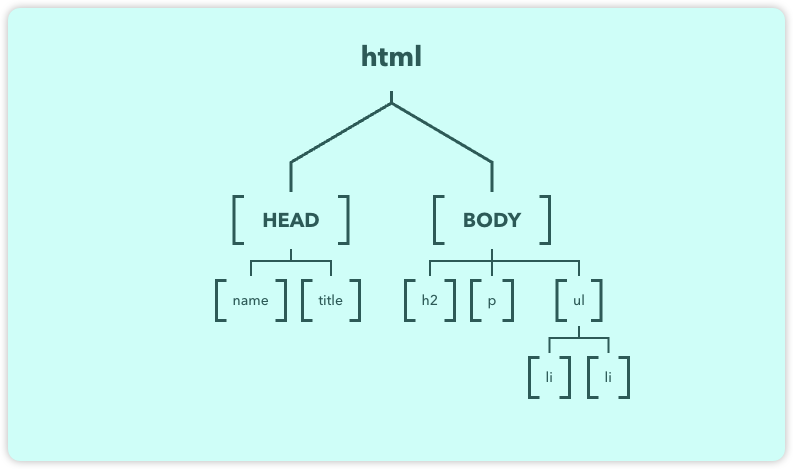
什么是DOM?(JavaScript DOM是什么?)
1、DOM简洁 DOM是js中最重要的一部分,没有DOM就不会通过js实现和用户之间的交互。 window是最大的浏览器对象,在它的下面还有很多子对象,我们要学习的DOM就是window对象下面的document对象 DOM(Document Object Model)…...

UIElement编辑器扩展 组件 Inspector
UIElement编辑器扩展 组件 Inspector https://docs.unity.cn/cn/2021.3/Manual/UIE-create-a-binding-uxml-inspector.html 简单开始 声明序列化VisualTreeAsset [SerializeField] VisualTreeAsset visualTree; 声明完,直接在脚本的Inspector面板,把你…...

Flask 3.x log全域配置(包含pytest)
最近使用到flask3.x,配置了全域的log,这边记录下 首先需要创建logging的配置文件,我是放在项目根目录的, Logging 配置 logging.json {"version": 1, # 配置文件版本号"formatters": {"default&qu…...

枚举算法(穷举法)(暴力法)
1.什么是枚举 枚举是指在一定范围内将所有情况一一列举,再通过条件判断得到自己想要的答案; 2.枚举核心 3.使用枚举的基本步骤 4.例题 4.1.我国古代数学家张丘建在他的《算经》一书中提出了著名的“百钱买百鸡”问题:鸡翁一值钱五;鸡母一值钱三;鸡雏三…...

计算机网络学习The next day
在计算机网络first day中,我们了解了计算机网络这个科目要学习什么,因特网的概述,三种信息交换方式等,在今天,我们就来一起学习一下计算机网络的定义和分类,以及计算机网络中常见的几个性能指标。 废话不多…...

ffmpeg中AVFrame解码linesize确定
一 测试环境 机型:Intel(R) Xeon(R) Gold 5218 ffmpeg版本4.3-dev 解码视频分辨率 720x1280 , 解码后 AVFrame linesize 768 解码视频分辨率 480x640, 解码后AVFrame linesize 512 二 linesize计算过程 avcodec_default_get_buffer2 -->update_frame_pool() --&g…...

数据可视化 | 期末复习 | 补档
文章目录 📚介绍可视化🐇什么是可视化🐇科学可视化,信息可视化,可视分析系统三者之间有什么区别🔥🐇可视化的基本流程🐇可视化的两个基本设计原则🐇数据属性🐇…...
【Docker】使用Docker安装Nginx及部署前后端分离项目应用
一、Nginx介绍 Nginx是一个高性能的HTTP和反向代理web服务器,同时也提供了IMAP/POP3/SMTP服务。它是由伊戈尔赛索耶夫为俄罗斯访问量第二的Rambler.ru站点开发的,公开版本1.19.6发布于2020年12月15日。其将源代码以类BSD许可证的形式发布,因它…...

28、web攻防——通用漏洞SQL注入HTTP头XFFCOOKIEPOST请求
文章目录 $_GET:接收get请求,传输少量数据,URL是有长度限制的; $_POST:接收post请求; $_COOKIE:接收cookie,用于身份验证; $_REQUEST:收集通过 GET 、POST和C…...

c++:类和对象(1),封装
C面向对象的三大特性:封装、继承、多态。 封装 封装的意义一: 将属性和行为作为一个整体,表现生活中的事物将属性和行为加以权限控制 类中的属性和行为,我们统一称为成员 属性也叫: 成员属性 成员变量 行为也叫&a…...
)
三、安全工程—安全架构(CISSP)
目录 一、安全工程 1.企业安全架构与系统安全架构 2.通用企业架构框架 2.1 Zachman框架...
《数组》)
Linux:shell脚本:基础使用(9)《数组》
数组就是一组数据类型相同集合 定义 数组名(元素内容…………) 如果没有元素内容就是空 arr1() # 定义了一个空数组 arr2(1 2 3 4 5 6 ) # 定义了一个元素是整形的数组 arr3("hello" "world" "你好" "世界") # 定义了一个元素为字符…...

TCP高并发服务器简介(select、poll、epoll实现与区别)
select、poll、epoll三者的实现: select实现TCP高并发服务器的流程: 一、创建套接字(socket函数):二、填充服务器的网络信息结构体:三、套接字和服务器的网络信息结构体进行绑定(bind函数&…...

Linux中的软件包管理器yum
目录 1.什么是软件包 2.关于 rzsz 3.查看软件包 4.如何安装软件 5.如何卸载软件 1.什么是软件包 ● 在Linux下安装软件, 一个通常的办法是下载到程序的源代码, 并进行编译, 得到可执行程序. ● 但是这样太麻烦了, 于是有些人把一些常用的软件提前编译好, 做成软件包(可以理…...
如何使用支付宝沙箱环境本地配置模拟支付并结合内网穿透远程调试
文章目录 前言1. 下载当面付demo2. 修改配置文件3. 打包成web服务4. 局域网测试5. 内网穿透6. 测试公网访问7. 配置二级子域名8. 测试使用固定二级子域名访问 正文开始前给大家推荐个网站,前些天发现了一个巨牛的 人工智能学习网站, 通俗易懂ÿ…...

解决子元素的click事件会触发父元素的dbclick事件
解决子元素的click事件会触发父元素的dbclick事件 方案一:方案二:方案三:方案一方案二综合案例如下: 方案一: 错误思路:通过阻止子元素click事件的冒泡,阻止父元素的dbclick 正确思路ÿ…...
)
算法训练营Day38(动态规划1)
动态规划理论基础 动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。 区别 动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心&…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
