【算法专题】动态规划之路径问题
动态规划2.0
- 动态规划 - - - 路径问题
- 1. 不同路径
- 2. 不同路径Ⅱ
- 3. 珠宝的最高价值
- 4. 下降路径最小和
- 5. 最小路径和
- 6. 地下城游戏
动态规划 - - - 路径问题
1. 不同路径
题目链接 -> Leetcode -62.不同路径
Leetcode -62.不同路径
题目:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右->向下->向下
- 向下->向下->向右
- 向下->向右->向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
- 1 <= m, n <= 100
- 题目数据保证答案小于等于 2 * 10^9
思路:
- 状态表示:对于这种「路径类」的问题,我们的状态表示一般有两种形式:
i. 从 [i, j] 位置出发,…;
ii. 从起始位置出发,到达 [i, j] 位置,…;
我们选择第二种定义状态表示的方式:dp[i][j] 表示:走到 [i, j] 位置处,一共有多少种方式。 - 状态转移方程:分析一下,如果 dp[i][j] 表示到达 [i, j] 位置的方法数,那么到达 [i, j] 位置之前的一小步,有两种情况:
i. 从 [i, j] 位置的上方( [i - 1, j] 的位置)向下走一步,转移到 [i, j] 位置;
ii. 从 [i, j] 位置的左方( [i, j - 1] 的位置)向右走一步,转移到 [i, j] 位置。
由于我们要求的是有多少种方法,因此状态转移方程就呼之欲出了: dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 。 - 返回值:根据状态表示,我们要返回 dp[m][n] 的值。
代码如下:
class Solution {public:int uniquePaths(int m, int n){// 多开一行一列,可以直接在循环内初始化vector<vector<int>> dp(m + 1, vector<int>(n + 1));dp[0][1] = 1; // 为了后面填表的正确// dp[i][j] 表示:⾛到 [i, j] 位置处,⼀共有多少种方式for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m][n];}};
2. 不同路径Ⅱ
题目链接 -> Leetcode -63.不同路径Ⅱ
Leetcode -63.不同路径Ⅱ
题目:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
输入:obstacleGrid = [[0, 0, 0], [0, 1, 0], [0, 0, 0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右->向右->向下->向下
- 向下->向下->向右->向右
示例 2:
输入:obstacleGrid = [[0, 1], [0, 0]]
输出:1
提示:
- m == obstacleGrid.length
- n == obstacleGrid[i].length
- 1 <= m, n <= 100
- obstacleGrid[i][j] 为 0 或 1
思路:本题为不同路径的变型,只不过有些地方有「障碍物」,只要在「状态转移」上稍加修改就可解决。
- 状态表示:dp[i][j] 表示:走到 [i, j] 位置处,一共有多少种方式。
- 状态转移:简单分析一下。如果 dp[i][j] 表示到达 [i, j] 位置的方法数,那么到达 [i, j] 位置之前的一小步,有两种情况:
i. 从 [i, j] 位置的上方( [i - 1, j] 的位置)向下走一步,转移到 [i, j] 位置;
ii. 从 [i, j] 位置的左方( [i, j - 1] 的位置)向右走一步,转移到 [i, j] 位置。
但是, [i - 1, j] 与 [i, j - 1] 位置都是可能有障碍的,此时从上面或者左边是不可能到达 [i, j] 位置的,也就是说,此时的方法数应该是 0;由此我们可以得出一个结论,只要这个位置上「有障碍物」,那么我们就不需要计算这个位置上的值,直接让它等于 0 即可。 - 返回值:根据状态表示,我们要返回的结果是 dp[m][n].
代码如下:
class Solution {public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid){int m = obstacleGrid.size(), n = obstacleGrid[0].size();// 多开一行一列方便初始化vector<vector<int>> dp(m + 1, vector<int>(n + 1));dp[0][1] = 1; // 为了后面填表的正确// dp[i][j] 表示:⾛到 [i, j] 位置处,⼀共有多少种方式for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){// 原矩阵中的位置不是障碍物if (obstacleGrid[i - 1][j - 1] != 1){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}}return dp[m][n];}};
3. 珠宝的最高价值
题目链接 -> Leetcode -LCR 166.珠宝的最高价值
Leetcode -LCR 166.珠宝的最高价值
题目:现有一个记作二维矩阵 frame 的珠宝架,其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为:
只能从架子的左上角开始拿珠宝
每次可以移动到右侧或下侧的相邻位置
到达珠宝架子的右下角时,停止拿取
注意:珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝,比如 frame = [[0]] 。
示例 1:
输入: frame = [[1, 3, 1], [1, 5, 1], [4, 2, 1]]
输出 : 12
解释 : 路径 1→3→5→2→1 可以拿到最高价值的珠宝
提示:
- 0 < frame.length <= 200
- 0 < frame[0].length <= 200
思路:本题的思路与上题的思路差不多,状态转移方程为:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j] .
代码如下:
class Solution {public:int maxValue(vector<vector<int>>& grid){int m = grid.size(), n = grid[0].size();// 多开一行一列方便初始化vector<vector<int>> dp(m + 1, vector<int>(n + 1));// dp[i][j] 表示:⾛到 [i, j] 位置处,此时的最大价值for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];}}return dp[m][n];}};
4. 下降路径最小和
题目链接 -> Leetcode -931.下降路径最小和
Leetcode -931.下降路径最小和
题目:给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。
在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。
具体来说,位置(row, col) 的下一个元素应当是(row + 1, col - 1)、(row + 1, col) 或者(row + 1, col + 1) 。
示例 1:
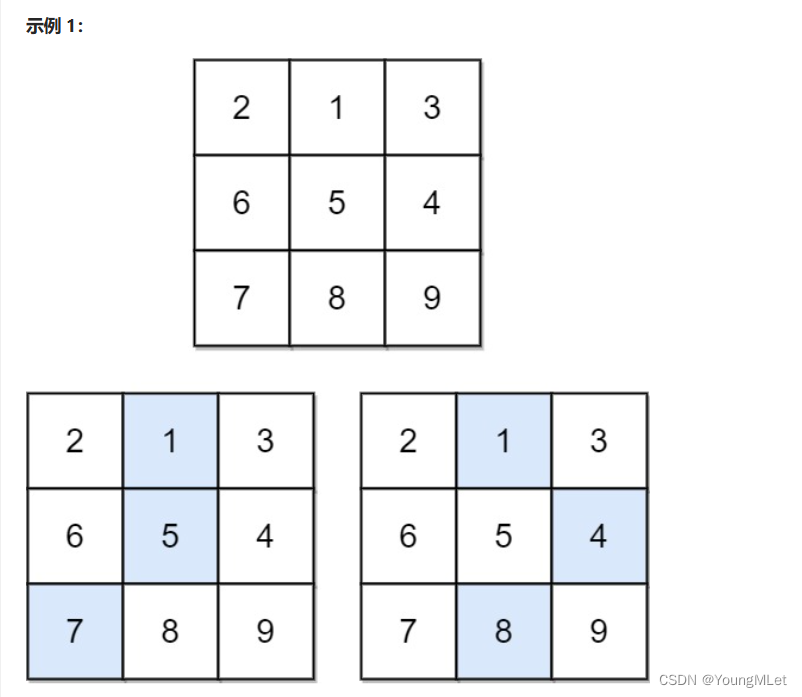
输入:matrix = [[2, 1, 3], [6, 5, 4], [7, 8, 9]]
输出:13
解释:如图所示,为和最小的两条下降路径
示例 2:
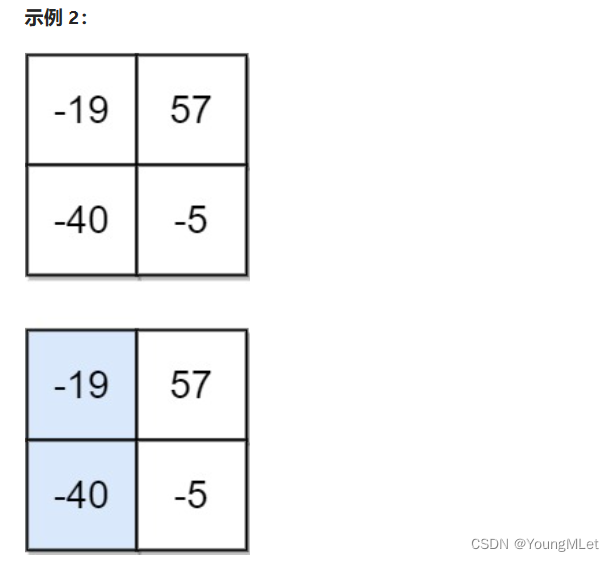
输入:matrix = [[-19, 57], [-40, -5]]
输出: - 59
解释:如图所示,为和最小的下降路径
提示:
- n == matrix.length == matrix[i].length
- 1 <= n <= 100
- 100 <= matrix[i][j] <= 100
思路:
- 状态表示:dp[i][j] 表示:到达 [i, j] 位置时,所有下降路径中的最小和。
- 状态转移方程:对于普遍位置 [i, j] ,根据题意得,到达 [i, j] 位置可能有三种情况:
i. 从正上方 [i - 1, j] 位置转移到 [i, j] 位置;
ii. 从左上方 [i - 1, j - 1] 位置转移到 [i, j] 位置;
iii. 从右上方 [i - 1, j + 1] 位置转移到 [i, j] 位置;
我们要的是三种情况下的「最小值」,然后再加上矩阵在 [i, j] 位置的值。
于是 dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i][j] 。 - 返回值:注意这里不是返回 dp[m][n] 的值;题目要求「只要到达最后一行」就行了,因此这里应该返回「 dp 表中最后一行的最小值」。
代码如下:
class Solution {public:int minFallingPathSum(vector<vector<int>>& matrix){int len = matrix.size();// 多开一行,两列,因为dp[i][j]的值需要用到dp[i - 1][j], dp[i - 1][j - 1], dp[i - 1][j + 1]vector<vector<int>> dp(len + 1, vector<int>(len + 2, INT_MAX));// 初始化,为了后面填表的正确性for (int i = 0; i <= len; i++) dp[0][i] = 0;// dp[i][j] 表示:到达 [i, j] 位置时,所有下降路径中的最小和for (int i = 1; i <= len; i++){for (int j = 1; j <= len; j++){dp[i][j] = min(min(dp[i - 1][j], dp[i - 1][j - 1]), dp[i - 1][j + 1]) + matrix[i - 1][j - 1];}}// 返回最后一行的最小值int ret = INT_MAX;for (int j = 0; j <= len; j++) ret = min(ret, dp[len][j]);return ret;}};
5. 最小路径和
题目链接 -> Leetcode -64.最小路径和
Leetcode -64.最小路径和
题目:给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
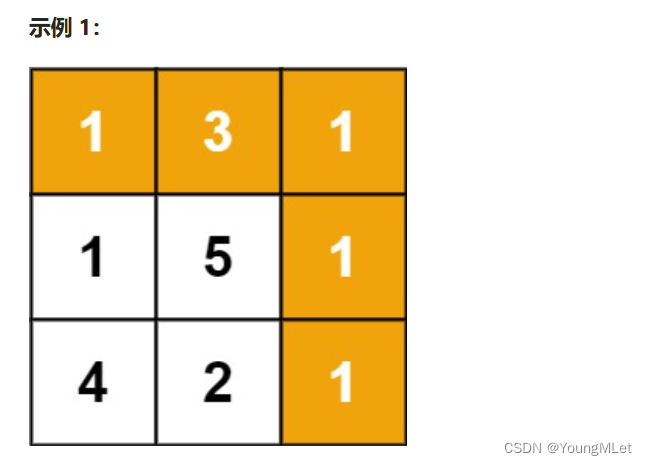
输入:grid = [[1, 3, 1], [1, 5, 1], [4, 2, 1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1, 2, 3], [4, 5, 6]]
输出:12
提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 200
思路:
- 状态表示:dp[i][j] 表示:到达 [i, j] 位置处,最小路径和是多少
- 状态转移:分析一下,如果 dp[i][j] 表示到达 [i, j] 位置处的最小路径和,那么到达[i, j] 位置之前的一小步,有两种情况:
i. 从 [i - 1, j] 向下走一步,转移到 [i, j] 位置;
ii. 从 [i, j - 1] 向右走一步,转移到 [i, j] 位置。
由于到 [i, j] 位置两种情况,并且我们要找的是最小路径,因此只需要这两种情况下的最小值,再加上 [i, j] 位置上本身的值即可。也就是: dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j] - 返回值:根据状态表示,我们要返回的结果是 dp[m][n].
代码如下:
class Solution {public:int minPathSum(vector<vector<int>>& grid){int m = grid.size(), n = grid[0].size();// dp[i][j] 表示:到达 [i, j] 位置处,最小路径和是多少vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));dp[0][1] = 0;for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];}}return dp[m][n];}};
6. 地下城游戏
题目链接 -> Leetcode -174.地下城游戏
Leetcode -174.地下城游戏
题目:恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。
我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);
其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:
输入:dungeon = [[-2, -3, 3], [-5, -10, 1], [10, 30, -5]]
输出:7
解释:如果骑士遵循最佳路径:右->右->下->下 ,则骑士的初始健康点数至少为 7 。
示例 2:
输入:dungeon = [[0]]
输出:1
提示:
- m == dungeon.length
- n == dungeon[i].length
- 1 <= m, n <= 200
- 1000 <= dungeon[i][j] <= 1000
思路:
- 状态表示:这道题如果我们定义成:从起点开始,到达 [i, j] 位置的时候,所需的最低初始健康点数。那么我们分析状态转移的时候会有一个问题:那就是我们当前的健康点数还会受到后面的路径的影响。也就是从上往下的状态转移不能很好地解决问题。
这个时候我们要换一种状态表示:从 [i, j] 位置出发,到达终点时所需要的最低初始健康点数。这样我们在分析状态转移的时候,后续的最佳状态就已经知晓。综上所述,定义状态表示为:dp[i][j] 表示:从 [i, j] 位置出发,到达终点时所需的最低初始健康点数。 - 状态转移方程:对于 dp[i][j] ,从 [i, j] 位置出发,下一步会有两种选择(为了方便理解,设 dp[i][j] 的最终答案是 x ):
i. 走到右边,然后走向终点;那么我们在 [i, j] 位置的最低健康点数加上这一个位置的消耗,应该要大于等于右边位置的最低健康点数,也就是: x + dungeon[i][j] >= dp[i][j + 1] ;通过移项可得: x >= dp[i][j + 1] - dungeon[i][j] 。因为我们要的是最小
值,因此这种情况下的 x = dp[i][j + 1] - dungeon[i][j] ;
ii. 走到下边,然后走向终点;那么我们在 [i, j] 位置的最低健康点数加上这⼀个位置的消耗,应该要大于等于下边位置的最低健康点数,也就是: x + dungeon[i][j] >= dp[i + 1][j] 。通过移项可得: x >= dp[i + 1][j] - dungeon[i][j] 。因为我们要的是最小值,因此这种情况下的 x = dp[i + 1][j] - dungeon[i][j] ;
- 综上所述,我们需要的是两种情况下的最小值,因此可得状态转移方程为:dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]
但是,如果当前位置的 dungeon[i][j] 是一个比较大的正数的话, dp[i][j] 的值可能变成 0 或者负数。也就是最低点数会小于 1 ,那么骑士就会死亡。因此我们求出来的 dp[i][j] 如果小于等于 0 的话,说明此时的最低初始值应该为 1 。处理这种情况仅需让 dp[i][j] 与 1 取一个最大值即可:dp[i][j] = max(1, dp[i][j])
-
初始化:可以在最前面加上一个「辅助结点」,帮助我们初始化。使用这种技巧要注意两个点:
i. 辅助结点里面的值要「保证后续填表是正确的」;
ii. 「下标的映射关系」。
在本题中,在 dp 表最后面添加一行,并且添加一列后,所有的值都先初始化为无穷大,然后让 dp[m][n - 1] = dp[m - 1][n] = 1 即可。 -
返回值:根据「状态表示」,我们需要返回 dp[0][0] 的值。
代码如下:
class Solution {public:int calculateMinimumHP(vector<vector<int>>& dungeon){int m = dungeon.size(), n = dungeon[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));dp[m][n - 1] = 1;// 从右下角往回推for (int i = m - 1; i >= 0; i--){for (int j = n - 1; j >= 0; j--){dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];// 如果减到负数,说明这里的血包很大,即使是负数到这里都可以,但是这是不符合常理的// 所以需要将这里置成 1 即可if (dp[i][j] <= 0) dp[i][j] = 1; }}// 返回最初位置return dp[0][0];}};
相关文章:

【算法专题】动态规划之路径问题
动态规划2.0 动态规划 - - - 路径问题1. 不同路径2. 不同路径Ⅱ3. 珠宝的最高价值4. 下降路径最小和5. 最小路径和6. 地下城游戏 动态规划 - - - 路径问题 1. 不同路径 题目链接 -> Leetcode -62.不同路径 Leetcode -62.不同路径 题目:一个机器人位于一个 m …...

Python range函数
Python中的range()函数是一个强大的工具,用于生成一系列的整数。它在循环、迭代和序列生成等方面都有广泛的应用。本文将深入探讨range()函数的用法,提供详细的示例代码,并讨论其在Python编程中的实际应用。 什么是range()函数? …...
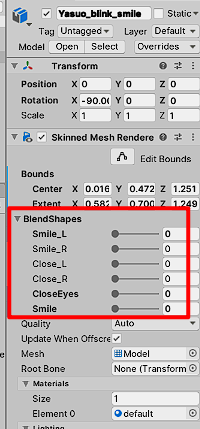
Unity中实现捏脸系统
前言 目前市面上常见的捏脸一般是基于BlendShapes和控制骨骼点坐标两种方案实现的。后者能够控制的精细程度更高,同时使用BlendShapes来控制表情。 控制骨骼点坐标 比如找到控制鼻子的骨骼节点修改localScale缩放,调节鼻子大小。 BlendShapes控制表…...
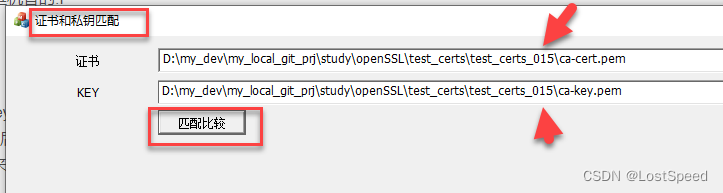
openssl3.2 - 检查rsa证书和私钥是否匹配(快速手搓一个工具)
文章目录 openssl3.2 - 检查rsa证书和私钥是否匹配(快速手搓一个工具)概述效果笔记编程环境界面控件的设置增加文件拖拽的类RSA证书和key是否匹配的实现在程序中加入环境变量备注备注END openssl3.2 - 检查rsa证书和私钥是否匹配(快速手搓一个工具) 概述 在学习openssl官方的…...
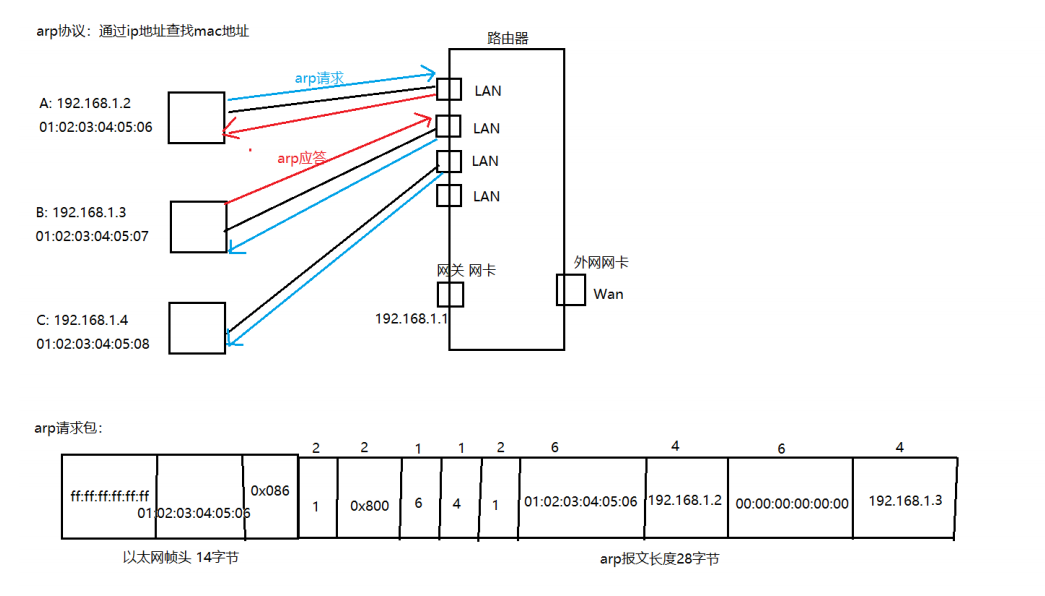
关于网络协议的笔记
简介: 协议, 网络协议的简称,网络协议是通信计算机双方必须共同遵从的一组约定。如怎么样建立连 接、怎么样互相识别等。只有遵守这个约定,计算机之间才能相互通信交流。它的 三要素是:语 法、语义、时序。 为了使数…...
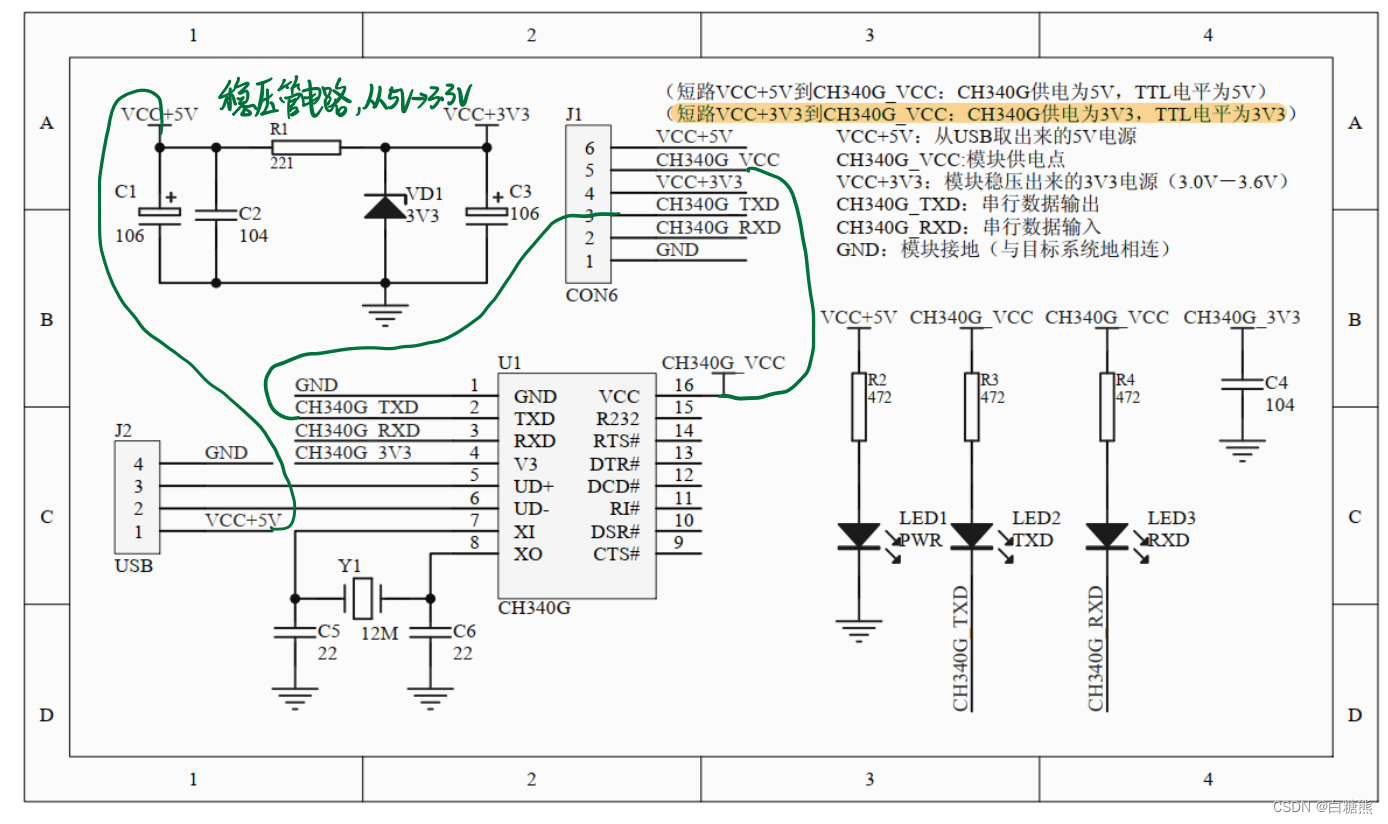
【江科大】STM32:USART串口(理论部分)上
串口 全双工:可以进行同步通信 单端信号:信号线传输的就是单端信号。(也就是与地线(GND)的电势差) 缺点:防干扰能力差 原因:当信号从A点传输到B点,理想条件是A࿰…...

深入了解Linux中常见的五种文件类型
了解文件类型对于正确理解和管理文件系统非常重要。希望本文能够帮助您更好地了解Linux中常见的文件类型及其在ls -l命令输出中的表示方式。 在Linux操作系统中,文件是操作系统中最基本的概念之一。在Linux中,每个文件都有一个特定的类型,这…...

SSM项目集成Spring Security 4.X版本(使用spring-security.xml 配置文件方式)
目录 前言 实战开发: 一、Spring Security整合到SSM项目 1. pom文件引入包 2. web.xml 配置 3. 添加 spring-security.xml 文件 二、Spring Security实战应用 1. 项目结构 2. pom文件引入 3. web.xml 配置 4. Spring 配置 applicationContext.xml 5. sp…...

如何生成开发语言的排名图表
1、解释说明 生成开发语言排名图表,通常需要以下几个步骤: - 首先,我们需要收集一些关于不同编程语言的统计数据,例如使用人数、市场份额等。这些数据可以从各种来源获取,例如网站、报告、数据库等。 - 然后&#x…...
有哪些简单好用、适合中小型企业的CRM系统?
阅读本文,你将了解:一、中小型企业对CRM系统的主要需求;二、盘点四款好用的CRM系统;三、CRM系统实施策略和优秀实践。 在快速变化的商业环境中,中小型企业面临着独特的挑战:如何在有限的资源下高效地管理客…...

Unity 适配器模式(实例详解)
文章目录 简介1. **Input Adapter 示例**2. **Component Adapter 示例**3. **网络数据解析适配器**4. **物理引擎适配**5. **跨平台服务适配** 简介 Unity中的适配器模式(Adapter Pattern)主要用于将一个类的接口转换为另一个接口,以便于原本…...

Spring boot项目java bean和xml互转
Spring boot项目实现java bean和xml互转 项目场景:互转方法使用jackson进行互转使用jaxws进行xml与bean的互转 搞定收工! 项目场景: 工作中需要给下游第三方收费系统做数据挡板,由于下游系统使用的是soap webservice,里面涉及各种…...
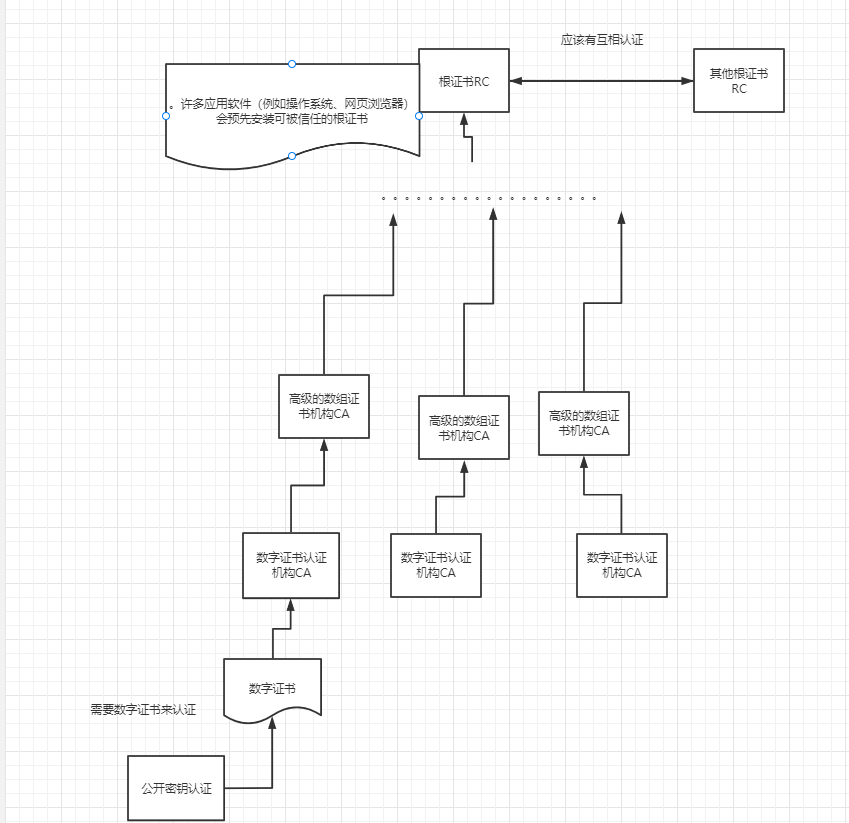
数字证书和数字证书认证机构和数字根证书,CA,RCA
文章目录 一、 数字证书1、什么是数字证书2、数字证书干什么的3、风险 二、数字证书认证机构(Certificate Authority,缩写为CA)参考文章 一、 数字证书 维基百科 公开密钥认证(英语:Public key certificateÿ…...

java web mvc-08-Grails 入门介绍
拓展阅读 Spring Web MVC-00-重学 mvc mvc-01-Model-View-Controller 概览 web mvc-03-JFinal web mvc-04-Apache Wicket web mvc-05-JSF JavaServer Faces web mvc-06-play framework intro web mvc-07-Vaadin web mvc-08-Grails 开源 The jdbc pool for java.(java …...

深度学习技术栈 —— Pytorch之TensorDataset、DataLoader
深度学习技术栈 —— Pytorch之TensorDataset、DataLoader 前言一、TensorDataset、DataLoader的用法?二、从.csv文件-->tensor张量总结 前言 简单来说,TensorDataset与DataLoader这两个类的作用, 就是将数据读入并做整合,以便…...
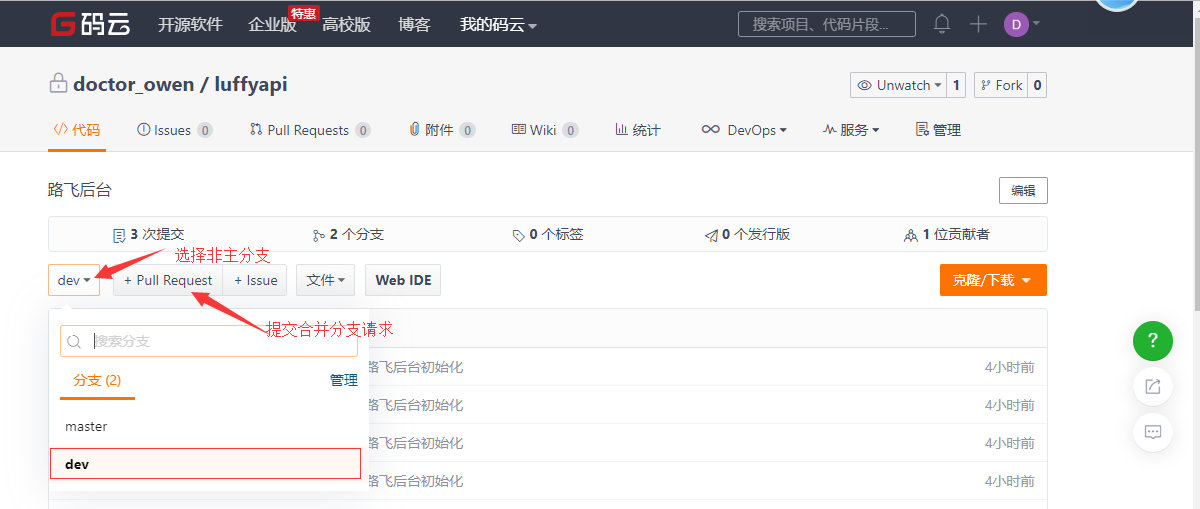
远程git开发
两种本地与远程仓库同步 """ 1)你作为项目仓库初始化人员:线上要创建空仓库 > 本地初始化好仓库 > 建立remote链接(remote add) > 提交本地仓库到远程(push)2)你作为项目后期开发人员:远程项目仓库已经创…...

Codeforces Round 812 (Div. 2) ---- C. Build Permutation --- 题解
目录 C. Build Permutation 题目描述: 编辑 思路解析: 代码实现: C. Build Permutation 题目描述: 思路解析: 先证明在任何情况下答案均存在。 假设我们所求的为 m m1 m2.....n 的排列,我们称不小于n…...
)
Matlab 将工作区变量保存到文件中(save)
语法 1、save(filename) 2、save(filename,variables) 3、save(filename,variables,fmt) 4、save(filename,variables,version) 5、save(filename,variables,version,-nocompression) 6、save(filename,variables,-append) 7、save(filename,variables,-append,-nocompression…...

源码实现简介
本系列所有代码在文章底部,每一章节代码可独立编译运行 随着科技的飞速发展,自动驾驶技术正逐渐成为现实。而在自动驾驶技术中,感知是至关重要的一个环节。通过感知,自动驾驶车辆能够识别和理解周围环境,进而做出相应…...

我每天如何使用 ChatGPT
我们都清楚互联网的运作方式——充斥着各种“爆款观点”,极端分裂的意见,恶搞和无知现象屡见不鲜。 最近,大家对于人工智能(AI)特别是大语言模型(LLMs)和生成式 AI(GenAI࿰…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...

vue3 vite.config.js 引入bem.scss文件报错
[sass] Can’t find stylesheet to import. ╷ 1 │ use “/bem.scss” as *; │ ^^^^^^^^^^^^^^^^^^^^^^ ╵ src\App.vue 1:1 root stylesheet 分析 我们遇到了一个在Vue3项目中使用Vite时,在vite.config.js中引入bem.scss文件报错的问题。错误信息指出在App.vue…...
