【数据结构】二叉树算法讲解(定义+算法原理+源码)
博主介绍:✌全网粉丝喜爱+、前后端领域优质创作者、本质互联网精神、坚持优质作品共享、掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战✌有需要可以联系作者我哦!
🍅附上相关C语言版源码讲解🍅
👇🏻 精彩专栏推荐订阅👇🏻 不然下次找不到哟
目录
一、二叉树定义(特点+结构)
二叉树算法性质:
二、算法实现(完整代码)
三、算法总结
二叉树的优点:
二叉树的缺点:
二叉树的应用:
小结
大家点赞、收藏、关注、评论啦 !
谢谢哦!如果不懂,欢迎大家下方讨论学习哦。
一、二叉树定义(特点+结构)
二叉树是一种树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树具有以下定义和特点:
1. 节点:二叉树是由节点构成的集合。每个节点包含三个基本信息:
- 数据元素(或称为节点值)。
- 指向左子节点的指针/引用。
- 指向右子节点的指针/引用。
2. 根节点: 二叉树中的一个节点被称为根节点,它是整个树的起始节点。一棵二叉树只有一个根节点。
3. 叶子节点:没有子节点的节点被称为叶子节点(或叶节点)。
4. 父节点和子节点: 每个节点都有一个父节点,除了根节点。父节点指向它的子节点。
5. 深度:一个节点的深度是从根节点到该节点的唯一路径的边的数量。根节点的深度为0。
6. 高度/深度: 一棵二叉树的高度(或深度)是树中任意节点的最大深度。
7. 子树:二叉树中的任意节点和它的所有子孙节点组成的集合被称为子树。
8. 二叉搜索树(BST):在二叉搜索树中,每个节点的左子树中的节点值都小于该节点的值,而右子树中的节点值都大于该节点的值。
9. 满二叉树:如果一棵深度为k,且有2^k - 1个节点的二叉树被称为满二叉树。
10. 完全二叉树:对于一棵深度为k的二叉树,除了最后一层外,其它各层的节点数都达到最大值,且最后一层的节点都集中在左边,被称为完全二叉树。
二叉树的定义为:
struct TreeNode {int val; // 节点值TreeNode *left; // 左子节点指针TreeNode *right; // 右子节点指针TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
上述定义为C++中使用类实现的二叉树节点定义,包含节点值、左子节点指针和右子节点指针。
二叉树算法性质:
你提到的这些性质描述了二叉搜索树(Binary Search Tree,BST)的一些重要特征。让我们逐一解释这些性质:
1. 将任何一个点看作Root节点,则这个点的左子树也是 Binary Search Tree:这表示二叉搜索树中每个节点的左子树都满足二叉搜索树的性质,即左子树上的节点值小于当前节点的值。
2. 将任何一个点看作Root节点,则这个点的右子树也是 Binary Search Tree:类似地,这表明每个节点的右子树都是一个二叉搜索树,右子树上的节点值大于当前节点的值。
3. Binary Search Tree中的最小节点,一定是整棵树中最左下的叶子节点:这是因为最小节点不会有左子节点,只能一直沿着左子树往下走,直到叶子节点。
4. Binary Search Tree中的最大节点,一定是整棵树中最右下的叶子节点:同样,最大节点不会有右子节点,只能一直沿着右子树往下走,直到叶子节点。
这些性质是二叉搜索树在节点排列和结构上的特点,它们使得在二叉搜索树上执行搜索、插入和删除等操作更加高效。通过遵循这些性质,可以确保在整个树结构中维持有序性,使得二叉搜索树成为一种常用的数据结构。
二、算法实现(完整代码)
通过二叉树实现A、B、C、D的简单应用
#include<iostream>
using namespace std;
typedef char DataType;
struct BiNode
{DataType data;BiNode *lchild,*rchild;
};
//(1)假设二叉树采用链接存储方式存储,分别编写一个二叉树先序遍历的递归
//算法和非递归算法。
class BiTree
{public:BiTree(){root=Create(root);}//构造函数,建立一颗二叉树~BiTree(){Release(root);}//析构函数,释放各个节点的存储空间void Preorder(){Preorder(root);}//前序遍历二叉树void Inorder(){Inorder(root);}//中序遍历二叉树void Postorder(){Postorder(root);}//后序遍历二叉树void Levelorder(){Levelorder(root);};//层序遍历二叉树private:BiNode *root;//指向根节点的头指针BiNode *Create(BiNode *bt);//构造函数调用void Release(BiNode *bt);//析构函数调用void Preorder(BiNode *bt);//前序遍历函数调用void Inorder(BiNode *bt);//中序遍历函数调用void Postorder(BiNode *bt);//后序遍历函数调用void Levelorder(BiNode *bt);//层序遍历函数调用
};
//前序遍历
void BiTree::Preorder(BiNode *bt)
{if(bt==NULL)return;//递归调用的结束条件else{cout<<bt->data<<" ";//访问根节点bt的数据域Preorder(bt->lchild);//前序递归遍历bt的左子树Preorder(bt->rchild);//前序递归遍历bt的右子树}
}
//中序遍历
void BiTree::Inorder(BiNode *bt)
{if(bt==NULL)return;//递归调用的结束条件else{Inorder(bt->lchild);//中序递归遍历bt的左子树cout<<bt->data<<" ";//访问根节点的数据域Inorder(bt->rchild);//中序递归遍历bt的右子树}
}
//后序遍历
void BiTree::Postorder(BiNode *bt)
{if(bt==NULL)return;//递归调用的结束条件else{Postorder(bt->lchild);//后序递归遍历bt的左子树Postorder(bt->rchild);//后序递归遍历bt的右子树cout<<bt->data<<" ";//访问根节点bt的数据域}
}
//层序遍历
void BiTree::Levelorder(BiNode *bt){BiNode *Q[100],*q=NULL;int front=-1,rear=-1;//队列初始化 if(root == NULL) return;//二叉树为空,算法结束Q[++rear]=root;//根指针入队while(front!=rear){//当队列非空时 q=Q[++front];//出队cout<<q->data<<" ";if(q->lchild!=NULL) Q[++rear]=q->lchild;if(q->rchild!=NULL) Q[++rear]=q->rchild; }
}
//创建二叉树
BiNode *BiTree::Create(BiNode *bt)
{static int i=0;char ch;string str="AB#D##C##";ch=str[i++];if(ch=='#')bt=NULL;//建立一棵空树 else {bt=new BiNode;bt->data=ch;//生成一个结点,数据域为chbt->lchild=Create(bt->lchild);//递归建立左子树bt->rchild=Create(bt->rchild);//递归建立右子树}return bt;
}
//销毁二叉树
void BiTree::Release(BiNode *bt)
{if(bt!=NULL){Release(bt->lchild);Release(bt->rchild);delete bt;}
}
int main()
{cout<<"创建一棵二叉树"<<endl;BiTree T;//创建一颗二叉树cout<<"---层序遍历---"<<endl;//A B C D T.Levelorder();cout<<endl;cout<<"---前序遍历---"<<endl;//A B D CT.Preorder();cout<<endl;cout<<"---中序遍历---"<<endl;//B D A CT.Inorder();cout<<endl;cout<<"---后序遍历---"<<endl;//D B C AT.Postorder();cout<<endl;return 0;
}执行结果:

序存储的完全二叉树递归先序遍历算法描述(C++)如下:
//完全二叉树的顺序存储结构
#include <iostream>
#include <string.h>
#define MaxSize 100
using namespace std;
typedef char DataType;
class Tree{public:Tree(string str);//构造函数void createTree();//创建二叉树 void seqPreorder(int i);//先序遍历二叉树 void seqInorder(int i);//中序遍历二叉树 void seqPostorder(int i);//后序遍历二叉树 private: DataType node[MaxSize];//结点中的数据元素int num=0;//二叉树结点个数 string str;
};Tree::Tree(string str){this->str = str;
} void Tree::createTree(){for(int i = 1;i < str.length()+1 ;i++){node[i]=str[i-1];num++;}node[0] = (char)num;
}//顺序存储的完全二叉树递归先序遍历算法描述(C++)如下:
void Tree::seqPreorder(int i){if(i==0)//递归调用的结束条件return;else{cout<<" "<<(char)node[i];//输出根结点if(2*i<=(char)node[0])seqPreorder(2*i);//先序遍历i的左子树elseseqPreorder(0);if(2*i+1<=(char)node[0])seqPreorder(2*i+1);//先序遍历i的右子树elseseqPreorder(0); }
} //顺序存储的完全二叉树递归中序遍历算法描述(C++)如下:
void Tree::seqInorder(int i){if(i==0)//递归调用的结束条件return;else{if(2*i<=(char)node[0])seqInorder(2*i);//中序遍历i的左子树elseseqInorder(0);cout<<" "<<(char)node[i];//输出根结点if(2*i+1<=(char)node[0])seqInorder(2*i+1);//中序遍历i的右子树elseseqInorder(0); }
} //顺序存储的完全二叉树递归后序遍历算法描述(C++)如下:
void Tree::seqPostorder(int i){if(i==0)//递归调用的结束条件return;else{if(2*i<=(char)node[0])seqPostorder(2*i);//后序遍历i的左子树elseseqPostorder(0);if(2*i+1<=(char)node[0])seqPostorder(2*i+1);//后序遍历i的右子树elseseqPostorder(0); cout<<" "<<(char)node[i];//输出根结点}
} // (2)一棵完全二叉树以顺序方式存储,设计一个递归算法,对该完全二叉树进
//行中序遍历。
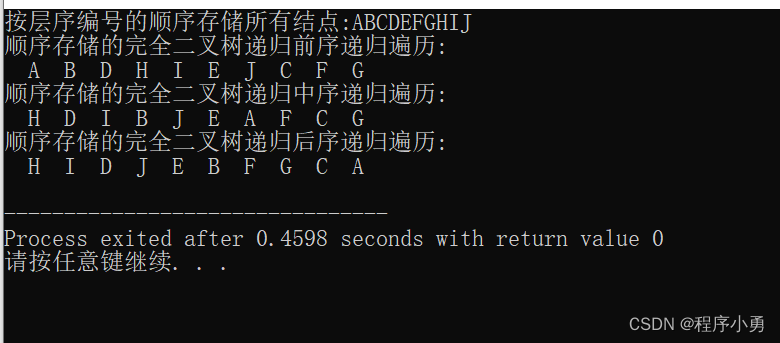
int main(){string str = "ABCDEFGHIJ";Tree T(str);//定义对象变量buscout<<"按层序编号的顺序存储所有结点:"<<str<<endl;T.createTree();cout<<"顺序存储的完全二叉树递归前序递归遍历:"<<endl; T.seqPreorder(1);cout<<endl; cout<<"顺序存储的完全二叉树递归中序递归遍历:"<<endl; T.seqInorder(1);cout<<endl; cout<<"顺序存储的完全二叉树递归后序递归遍历:"<<endl; T.seqPostorder(1);cout<<endl; return 0;
}
三、算法总结
二叉树的优点:
1. 快速查找: 在二叉搜索树(BST)中,查找某个元素的时间复杂度是O(log n),这使得二叉树在查找操作上非常高效。
2. 有序性:BST保持元素的有序性,对于某些应用场景,如快速查找最小值、最大值或在某一范围内的值,二叉树非常有用。
3. 容易插入和删除:在BST中,插入和删除操作相对容易,不需要像其他数据结构一样频繁地移动元素。
4. 中序遍历:通过中序遍历二叉搜索树,可以得到有序的元素序列,这对于某些应用(如构建有序列表)很方便。
二叉树的缺点:
1. 平衡性:如果不平衡,二叉搜索树的性能可能下降为线性级别,而不再是对数级别。因此,需要采取额外的措施来保持树的平衡,如 AVL 树或红黑树。
2. 对数据分布敏感: 对于某些特定的数据分布,比如按顺序插入的数据,可能导致二叉搜索树退化成链表,性能下降。
二叉树的应用:
1. 数据库索引:在数据库中,二叉搜索树被广泛应用于构建索引结构,以加速数据的检索。
2. 表达式解析:二叉树可用于构建表达式树,用于解析和求解数学表达式。
3. 哈夫曼编码:二叉树用于构建哈夫曼树,实现有效的数据压缩算法。
4. 文件系统:在文件系统的目录结构中,可以使用二叉树来组织和管理文件。
5. 网络路由:用于构建路由表,支持快速而有效的网络数据包路由。
6. 编译器设计: 语法分析阶段通常使用二叉树来构建语法树,以便后续的编译步骤。
7. 游戏开发:在游戏开发中,二叉树可以用于实现场景图、动画系统等。
8. 排序算法:一些排序算法,如快速排序,就是通过构建和操作二叉树来实现的。
总体而言,二叉树在计算机科学领域的应用非常广泛,它的特性使得它适用于多种数据管理和搜索场景。在实际应用中,需要根据具体情况选择合适的二叉树变体以及适当的平衡策略。
大家点赞、收藏、关注、评论啦 !
谢谢哦!如果不懂,欢迎大家下方讨论学习哦。
相关文章:

【数据结构】二叉树算法讲解(定义+算法原理+源码)
博主介绍:✌全网粉丝喜爱、前后端领域优质创作者、本质互联网精神、坚持优质作品共享、掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战✌有需要可以联系作者我哦! 🍅附上相关C语言版源码讲解🍅 ὄ…...
是什么?根组件模板又是什么?)
Vue3基础:挂载事例方法.mount()是什么?根组件模板又是什么?
.mount() <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Vue 3 演示</title> </head>…...
Unity渲染与Shader篇 【全面总结 | 持续更新】)
Unity 面试篇|(七)Unity渲染与Shader篇 【全面总结 | 持续更新】
目录 1.问一个Terrain,分别贴3张,4张,5张地表贴图,渲染速度有什么区别?为什么?2.什么是LightMap?3.MipMap是什么,作用?4.请问alpha test在何时使用?能达到什么…...

记录一些多维数组的方法
文章目录 前言一、获取多维数组的数据二、多维数组自带的方法总结 前言 验证过程中,我们经常会用到多维数组存储数据,本文主要记录一下,如何去获取我们需要的数据,以及多维数组自带的一些方法。 一、获取多维数组的数据 获取多维…...

Linux:gcc的相关知识
目录 gcc的翻译(编译)过程: 预处理: 条件编译: 编译: 汇编&链接: 什么是链接? 安装静态库: 静态库的使用: 动态静态的对比: 优缺对比…...

Linux的奇妙冒险———vim的用法和本地配置
vim的用法和本地配置 一.vim的组成和功能。1.什么是vim2.vim的多种模式 二.文本编辑(普通模式)的快捷使用1.快速复制,粘贴,剪切。2.撤销,返回上一步操作3.光标的控制4.文本快捷变换5.批量化操作和注释 三.底行模式四.v…...
微信小程序底部按钮适配iPhoneX以上,显示遮挡问题
只需要在给底部按钮加个样式 /* 底部导航栏容器 */ .button-box {/* 使用 safe-area-inset-bottom 属性适配 iPhone X 及以上型号设备 */padding-bottom: constant(safe-area-inset-bottom);padding-bottom: env(safe-area-inset-bottom);/* 其他样式属性 */ }iPhone6/7/8效果 …...
)
Qt容器QMap(映射)
插入数据 QMap<QString,QString> infoMap; //第一个是key 第二个是valueinfoMap.insert("王祖蓝","163cm");infoMap.insert("Anglebaby","168cm");infoMap["易烊千玺"] "173cm(成长中)";infoMap["姚…...

AI时代的创新工具:如何利用AI生成独具个性的XMind思维导图?
哈喽,大家好,我是木头左,物联网搬砖工一名,致力于为大家淘出更多好用的AI工具! 背景 随着互联网的发展,越来越多的人开始使用Markdown来编写文档。Markdown是一种轻量级的标记语言,它允许人们使…...

【每日一题】最长交替子数组
文章目录 Tag题目来源解题思路方法一:双层循环方法二:单层循环 写在最后 Tag 【双层循环】【单层循环】【数组】【2024-01-23】 题目来源 2765. 最长交替子数组 解题思路 两个方法,一个是双层循环,一个是单层循环。 方法一&am…...

gin数据解析和绑定
1. Json 数据解析和绑定 客户端传参,后端接收并解析到结构体 package mainimport ("github.com/gin-gonic/gin""net/http" )// 定义接收数据的结构体 type Login struct {// binding:"required"修饰的字段,若接收为空值…...
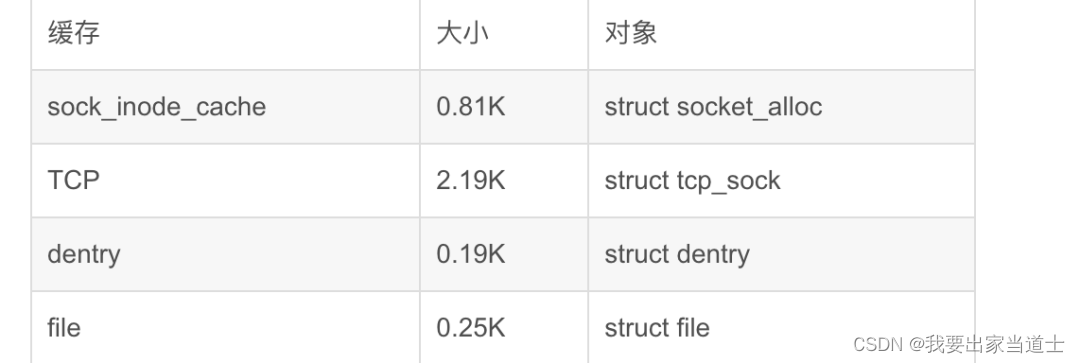
TCP服务器最多支持多少客户端连接
目录 一、理论数值 二、实际部署 参考 一、理论数值 首先知道一个基础概念,对于一个 TCP 连接可以使用四元组(src_ip, src_port, dst_ip, dst_port)进行唯一标识。因为服务端 IP 和 Port 是固定的(如下图中的bind阶段࿰…...

UML类图学习
UML类图学习 UML类图是描述类之间的关系概念1.类(Class):使用三层矩形框表示2.接口(interface):使用两层矩形框表示,与类图主要区别在于顶端有<<interface>>显示3、继承类(extends):用空心三角…...

死锁面试题详解
什么是死锁? 死锁是指两个或多个进程在执行过程中,因争夺资源而造成的一种相互等待的现象,如果没有外力干涉,这些进程将永远无法继续执行 死锁通常发生在多个进程试图同时访问同一资源而无法获取的情况下,例如&#…...

【rust/bevy】使用points构造ConvexMesh
目录 说在前面问题提出Rapier具体实现参考 说在前面 操作系统:win11rust版本:rustc 1.77.0-nightlybevy版本:0.12github:这里 问题提出 在three.js中,可以通过使用ConvexGeometry从给定的三维点集合生成凸包(Convex Hu…...

【C语言】string.h——主要函数总结
string.h主要定义了字符串处理函数和内存操作函数。 字符串处理函数 strlen() 功能:strlen()函数返回字符串的字节长度,不包括末尾的空字符\0。 函数原型:size_t strlen(const char* s); 返回值:返回的是size_t类型的无符号整…...

如何在前端优化中减少页面加载时间?
在前端优化中,减少页面加载时间是至关重要的,因为快速加载的页面可以提高用户体验,减少跳出率,从而提升网站的整体性能。本文将介绍一些实用的前端优化技巧,以帮助您减少页面加载时间。 一、优化图片 图片是页面加载…...

Typecho后台无法登录显示503 service unavailable问题及处理
一、Typecho 我的博客地址:https://www.aomanhao.top 使用老薛主机动态Typecho博客框架handsome主题的搭配,文章内容可以异地网页更新,可以听后台背景音乐,很好的满足我的痛点需求,博客部署在云端服务器访问响应较快…...

Python入门(一)
anaconda安装 官网:https://www.anaconda.com下载 jupyter lab 简介: 包含了Jupyter Notebook所有功能。 JupyterLab作为一种基于web的集成开发环境,你可以使用它编写notebook,操作终端,编辑markdown文本…...
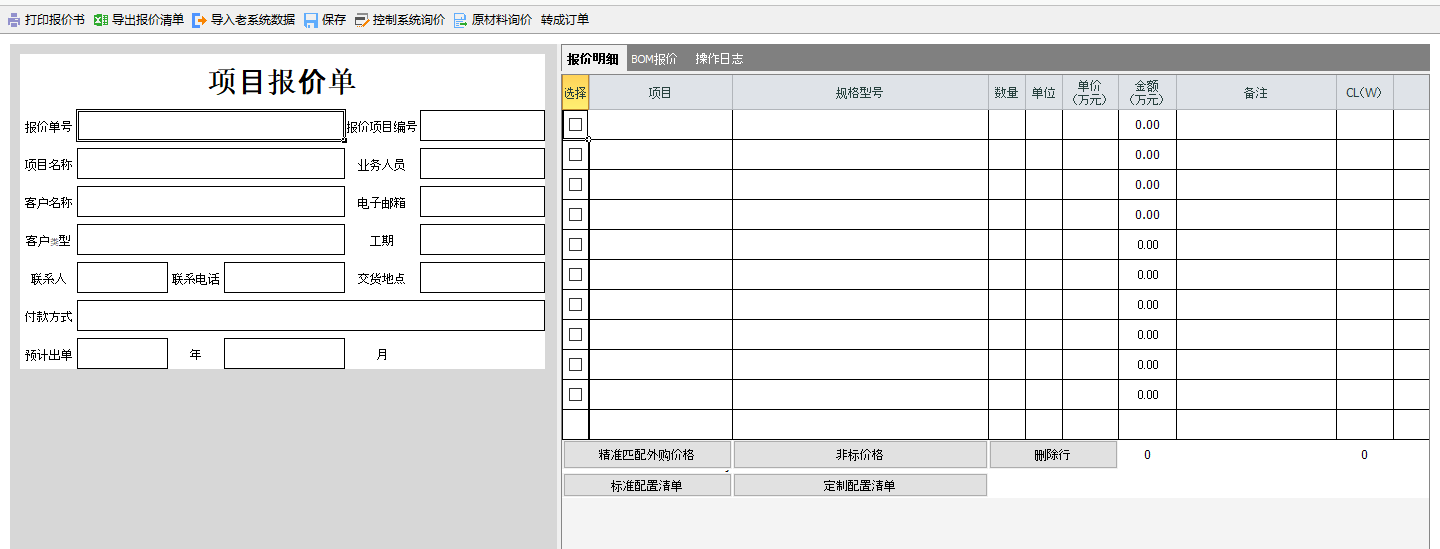
云表企业级无代码案例-自主开发ERP管理系统
痛点 我是一名企业经营者,同时也是信息化建设的坚定倡导者。凭借管理专业背景,我深知经营数据对于企业的至关重要性。如何高效搜集、精准分析经营数据,并将其转化为决策依据,直接关乎企业的生死存亡。太多因盲目决策而倒闭的企业…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
