科技赋能智慧水利——山海鲸软件水利方案解析
作为山海鲸可视化软件的开发者,我们深感荣幸能为我国智慧水利建设提供强大助力。作为钻研数字孪生领域的开创者,我们希望不仅能为大家带来免费好用,人人都能用起来的数字孪生产品,还希望以其独特的技术优势和创新设计理念,为各领域数字化改革发展做出贡献。
下面就带大家了解一下山海鲸智慧水利系列解决方案。
山海鲸智慧水利解决方案依托先进的大数据、云计算以及人工智能等前沿科技,将复杂的水利信息转化为直观易懂的可视化形式。通过整合地理信息系统(GIS)、遥感监测数据及实时水文气象信息,实现对江河湖库、水利工程设施的全方位、立体化动态展现与智能分析。

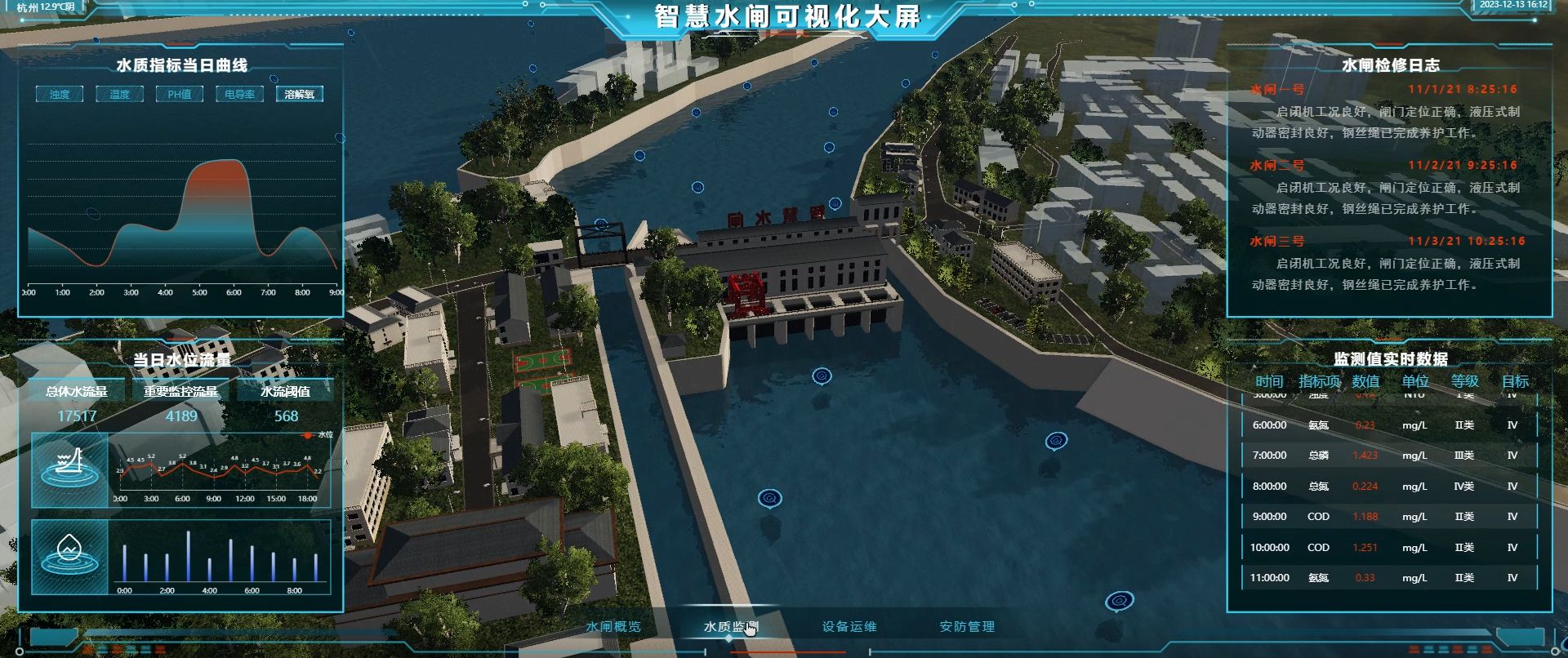
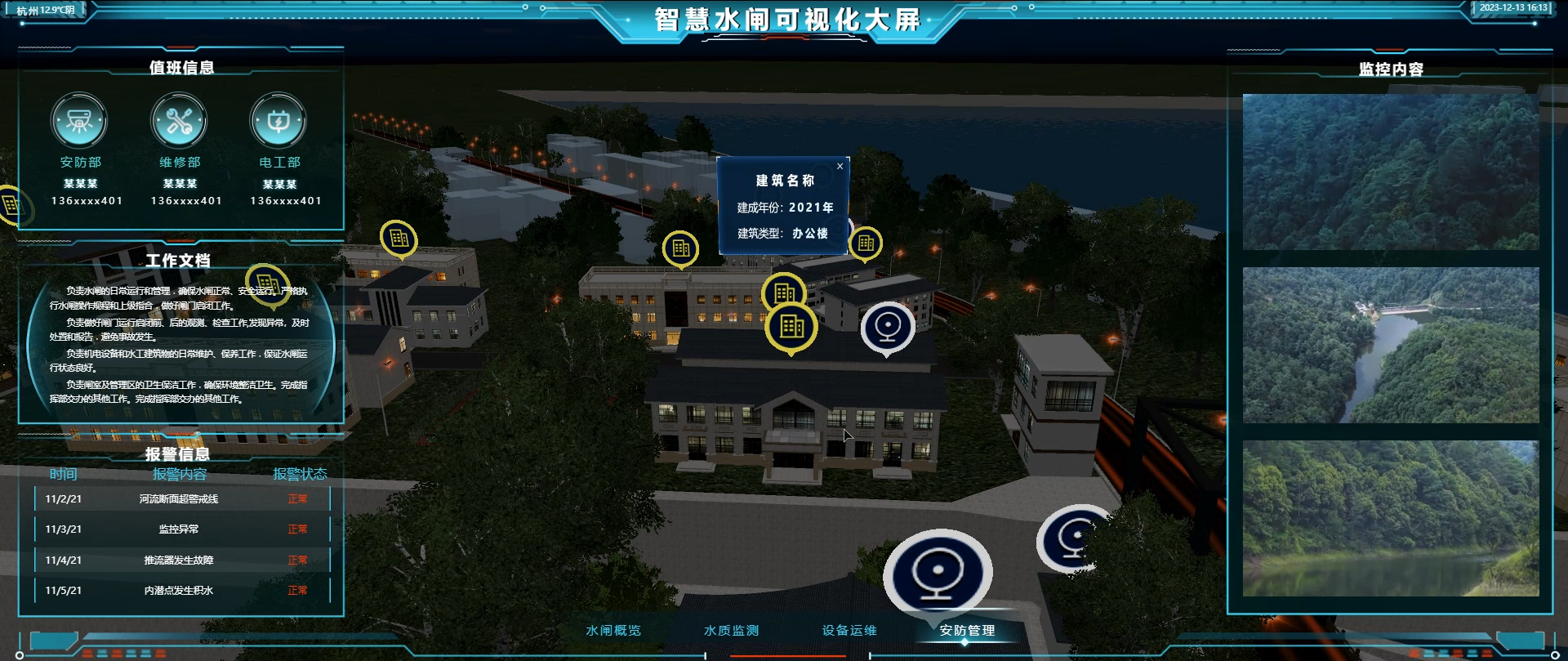
从水源地保护到水资源调度,从防汛抗旱预警到水质安全监控,山海鲸可视化软件如同一双洞察秋毫的眼睛,帮助决策者准确把握全局,科学决策。在实际应用中,山海鲸可视化软件能够实现实时水情数据可视化展示,无论是水库蓄水量变化、河流流量流速,还是地下水位波动,均能在数字大屏上以图表、地图等形式生动呈现,使管理者对各类水情了如指掌。


同时,结合AI预测模型,可提前预判可能出现的洪涝、干旱等情况,从而有效提升应急响应能力和水资源管理效能。不仅如此,山海鲸智慧水利还关注水资源的可持续利用,通过精准计量和优化配置,推动节水型社会建设。其强大的数据分析能力,有助于深入挖掘水利数据价值,为政策制定、项目规划提供有力的数据支撑。

总的来说,山海鲸可视化软件致力于构建全面、智能、高效的水利管理体系,用科技力量赋能智慧水利,守护绿水青山,服务国计民生。未来,我们将继续砥砺前行,不断探索技术创新,推动我国水利事业向更高质量发展迈进。
相关文章:

科技赋能智慧水利——山海鲸软件水利方案解析
作为山海鲸可视化软件的开发者,我们深感荣幸能为我国智慧水利建设提供强大助力。作为钻研数字孪生领域的开创者,我们希望不仅能为大家带来免费好用,人人都能用起来的数字孪生产品,还希望以其独特的技术优势和创新设计理念…...

C4.5决策树的基本建模流程
C4.5决策树的基本建模流程 作为ID3算法的升级版,C4.5在三个方面对ID3进行了优化: (1)它引入了信息值(information value)的概念来修正信息熵的计算结果,以抑制ID3更偏向于选择具有更多分类水平…...
)
本科毕业设计过程中应该锻炼的能力 (深度学习方向)
摘要: 本文以本科毕业设计做深度学习方向, 特别是全波形反演为例, 描述学生应在此过程中锻炼的能力. 搭建环境的能力. 包括 Python, PyTorch 等环境的安装.采集数据的能力. 包括 OpenFWI 等数据集.查阅资料的能力. 包括自己主要参考的文献, 以及其它相关文献 (不少于 20 篇). …...

深度学习——pycharm远程连接
目录 远程环境配置本地环境配置(注意看假设!!!这是很多博客里没写的)步骤1步骤2步骤2.1 配置Connection步骤2.2 配置Mappings 步骤3 配置本地项目的远程解释器技巧1 pycharm中远程终端连接技巧2 远程目录技巧3 上传代码文件技巧4 …...

信号量机制解决经典同步互斥问题
生产者 / 消费者问题、读者 / 写者问题和哲学家问题是操作系统的三大经典同步互斥问题。本文将介绍这三个问题的基本特点以及如何用信号量机制进行解决。 在分析这三个问题之前,我们首先需要了解用信号量机制解决同步互斥问题的一般规律: 实现同步与互斥…...
的区别,附代码举例)
java基础09-==和equals()的区别,附代码举例
和equals()的区别 在Java中,和equals()是两个不同的运算符,它们在比较对象时有着本质的区别。 运算符: 用于比较两个基本数据类型(如int、char等)或两个对象的引用。 当用于比较基本数据类型时,它会比较它们的值。 当…...
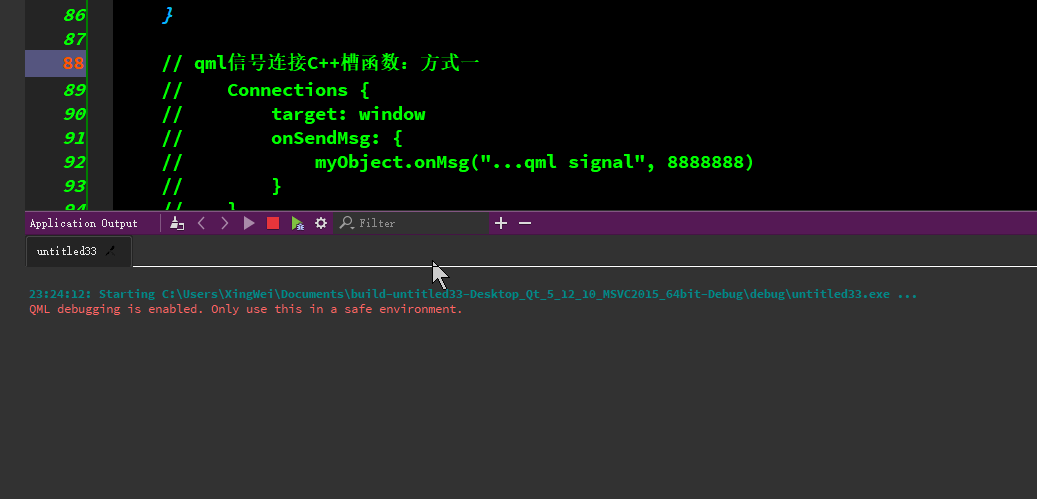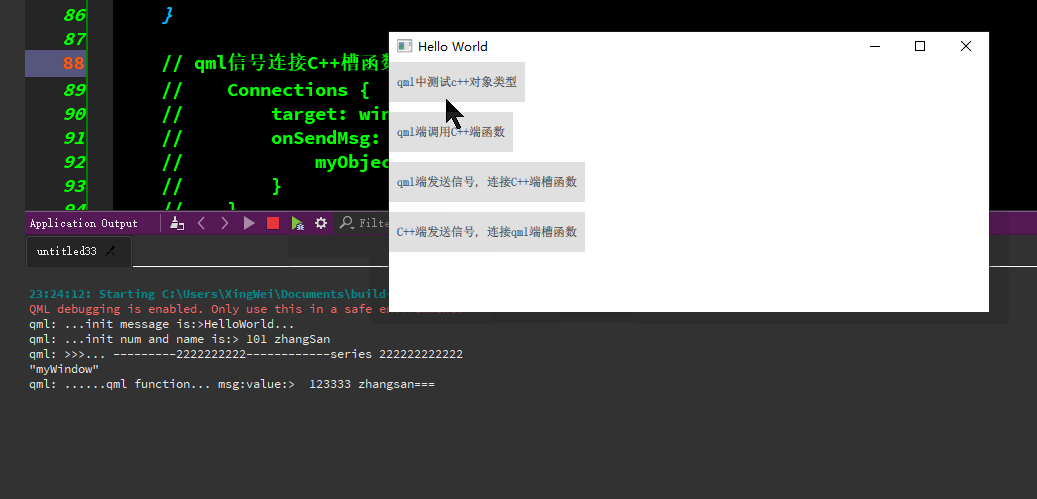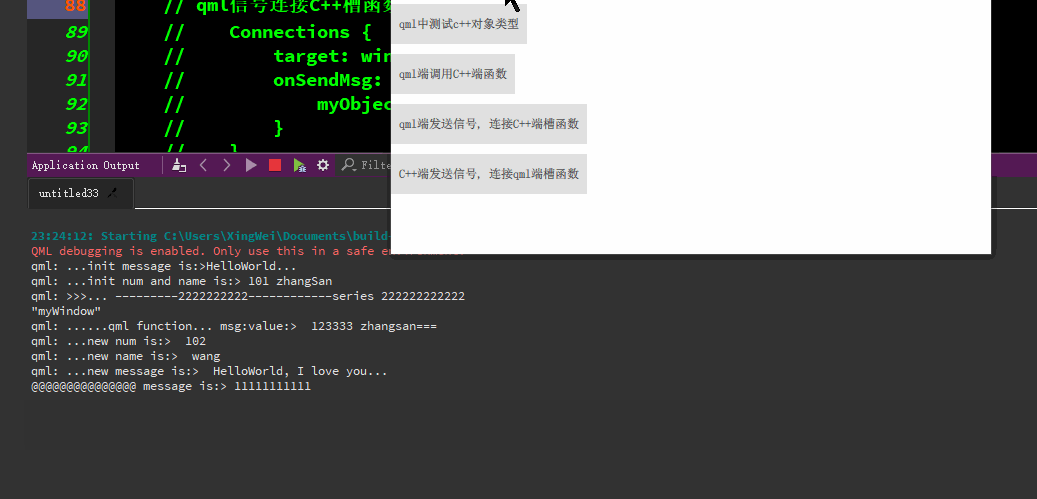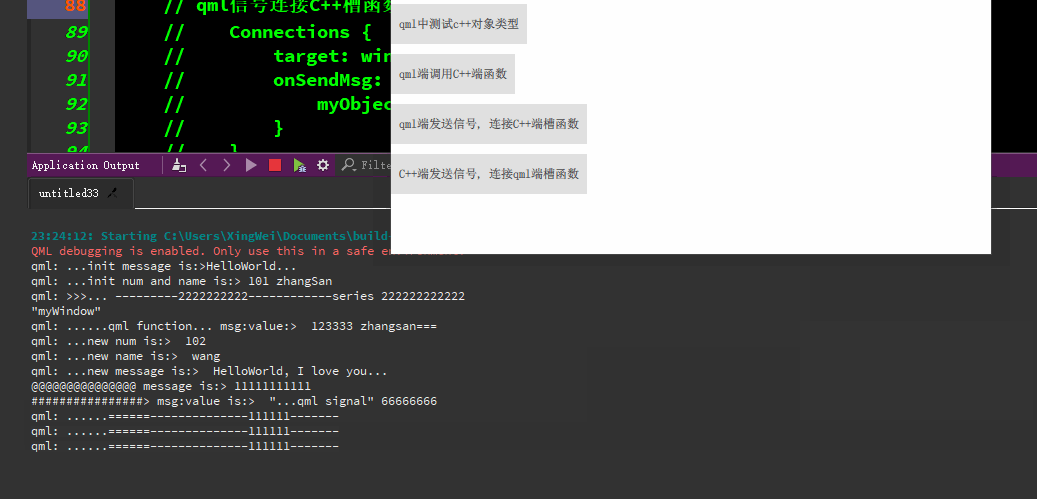
qml与C++的交互
qml端使用C对象类型、qml端调用C函数/c端调用qml端函数、qml端发信号-连接C端槽函数、C端发信号-连接qml端函数等。 代码资源下载: https://download.csdn.net/download/TianYanRen111/88779433 若无法下载,直接拷贝以下代码测试即可。 main.cpp #incl…...
LabVIEW电路板插件焊点自动检测系统
LabVIEW电路板插件焊点自动检测系统 介绍了电路板插件焊点的自动检测装置设计。项目的核心是使用LabVIEW软件,开发出一个能够自动检测电路板上桥接、虚焊、漏焊和多锡等焊点缺陷的系统。 系统包括成像单元、机械传动单元和软件处理单元。首先,利用工业相…...
第十一站:多态练习ODU
实现动态切换 ODU.h #pragma once #include <iostream> using namespace std; #define ODU_TYPE_311_FLAG "311" #define ODU_TYPE_335_FLAG "335" enum class ODU_TYPE {ODU_TYPE_311,ODU_TYPE_335,ODU_TYPE_UNKNOW };class ODU{ public:ODU();//发…...

【深度学习】详解利用Matlab和Python中 LSTM 网络实现序列分类
🔗 运行环境:Matlab、Python 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 🔐#### 防伪水印——左手の明天 ####🔐 💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗 💗今天分享Matlab深度学习—— LSTM 网络实现序列分...

Unity 工厂方法模式(实例详解)
文章目录 在Unity中,工厂方法模式是一种创建对象的常用设计模式,它提供了一个接口用于创建对象,而具体的产品类是由子类决定的。这样可以将对象的创建过程与使用过程解耦,使得代码更加灵活和可扩展。 工厂模式的主要优点如下&…...

2024年美赛数学建模思路 - 案例:异常检测
文章目录 赛题思路一、简介 -- 关于异常检测异常检测监督学习 二、异常检测算法2. 箱线图分析3. 基于距离/密度4. 基于划分思想 建模资料 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 一、简介 – 关于异常…...

一键完成,批量转换HTML为PDF格式的方法,提升办公效率
在当今数字化的时代,HTML和PDF已经成为两种最常用的文件格式。HTML用于网页内容的展示,而PDF则以其高度的可读性和不依赖于平台的特性,成为文档分享和传播的首选格式。然而,在办公环境中,我们经常需要在这两种格式之间…...

【重点问题】攻击面发现及管理
Q1:在使用长亭云图极速版时,是否需要增设白名单扫描节点? 长亭云图极速版高级网络安全产品基于一种理念,即攻击面发现是一个不断变换且需要持续对抗的过程。在理想的情况下,用户应当在所有预置防护设施发挥作用的环境…...

UE4外包团队:国外使用UE4虚幻引擎制作的十个知名游戏
1.俄罗斯方块效果(任天堂 Switch、PlayStation 4、PC、Xbox) 2.耀西的手工世界(任天堂 Switch) 3. Final Fantasy 7 Remake Intergrade (PlayStation, PC) 4.《堡垒之夜》(PC、Nintendo Switch、PlayStation、Xb…...
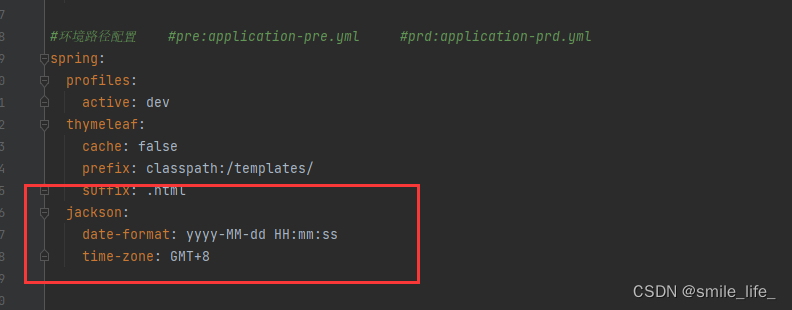
解决springboot+mybatisplus返回时间格式带T
原因:我service实现类的代码是 Overridepublic Map<String, Object> queryDictPage(Map<String, Object> queryMap) {Map<String,Object> map new HashMap<>();QueryWrapper<Dict> wrapper new QueryWrapper<>(); // …...
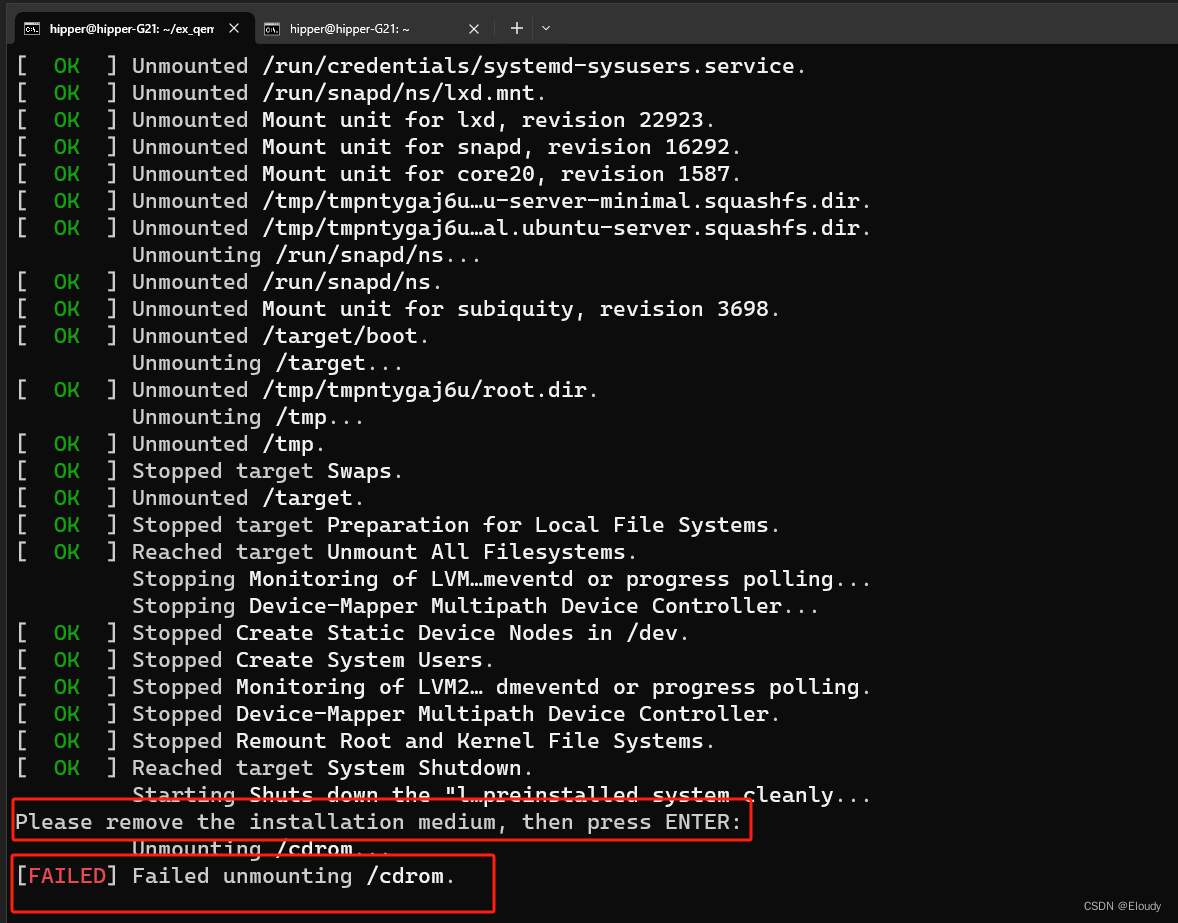
纯命令行在Ubuntu中安装qemu的ubuntu虚拟机,成功备忘
信息总体还算完整,有个别软件更新了名字,所以在这备忘一下 1. 验证kvm是否支持 ________________________________________________________________ $ grep vmx /proc/cpuinfo __________________________________________________________________…...

Vue的学习Day1_是什么以及两种风格
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、Vue是什么?二、渐进式框架1.渐进式 三、Vue API风格1.选项式 API (Options API)2.组合式 API (Composition API) 四、Vue 开发前的准备 前言 放…...
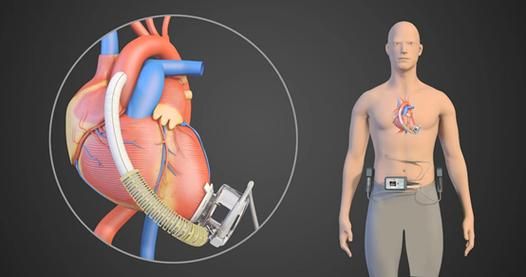
磁悬浮人工心脏的不良事件分析:美国FDA数据库的启示
引言: 左心室辅助装置(LVAD)是治疗末期难治性心力衰竭(HF)患者的有效手段。磁悬浮人工心脏HeartMate-3(磁悬浮人工心脏)作为第三代LVAD,自2017年获得美国食品药品监督管理局&#x…...

HarmonyOS(十二)——全面认识HarmonyOS三种渲染控制
渲染控制概述 ArkUI通过自定义组件的build()函数和builder装饰器中的声明式UI描述语句构建相应的UI。在声明式描述语句中开发者除了使用系统组件外,还可以使用渲染控制语句来辅助UI的构建,这些渲染控制语句包括控制组件是否显示的条件渲染语句ÿ…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
