【学习笔记】CF1349F2 Slime and Sequences (Hard Version)
多项式工业警告!!!
点击看题意
思路来自 这位大佬 。
为什么这么好的题解没人评论。
Part 1
前置知识:拉格朗日反演(多项式复合),分式域(引入负整数次项)。
条件:有两个幂级数 F ( x ) , G ( x ) F(x),G(x) F(x),G(x),有 G ( F ( x ) ) = x G(F(x))=x G(F(x))=x,即 F , G F,G F,G互为复合逆。
F , G F,G F,G应常系数为 0 0 0且 [ x 1 ] [x^1] [x1]系数非 0 0 0。
首先引入分式域。对于无法求逆的整式 F ( x ) F(x) F(x),找出 G ( x ) = F ( x ) / x k G(x)=F(x)/x^k G(x)=F(x)/xk,则 1 F ( x ) = x − k 1 G ( x ) \frac{1}{F(x)}=x^{-k}\frac{1}{G(x)} F(x)1=x−kG(x)1。这也说明了分式域下存在负指数(这通常在对整式求逆时出现)。注意,此时乘法卷积仍然是良定义。
引理:(默认 F ( x ) F(x) F(x)满足上述条件)
[ x − 1 ] F ′ ( x ) F ( x ) k = [ k = − 1 ] [x^{-1}]F'(x)F(x)^k=[k=-1] [x−1]F′(x)F(x)k=[k=−1]
证明:当 k ≠ − 1 k\ne -1 k=−1时左式可以看作 ( 1 k + 1 F ( x ) k + 1 ) ′ (\frac{1}{k+1}F(x)^{k+1})' (k+11F(x)k+1)′,而求导不可能产生 [ x − 1 ] [x^{-1}] [x−1]项( ln ( x ) \ln (x) ln(x)是例外,但是在 x = 0 x=0 x=0处无定义,所以不合法);当 k = − 1 k=-1 k=−1时可以验证答案就是 1 1 1。
扩展拉格朗日反演:
[ x n ] H ( G ( x ) ) = 1 n [ x n − 1 ] H ′ ( x ) ( x F ( x ) ) n [x^n]H(G(x))=\frac{1}{n}[x^{n-1}]H'(x)\left(\frac{x}{F(x)}\right)^n [xn]H(G(x))=n1[xn−1]H′(x)(F(x)x)n
另类扩展拉格朗日反演:
[ x n ] H ( G ( x ) ) = [ x n ] H ( x ) ( x F ( x ) ) n + 1 F ′ ( x ) [x^n]H(G(x))=[x^n]H(x)\left(\frac{x}{F(x)}\right)^{n+1}F'(x) [xn]H(G(x))=[xn]H(x)(F(x)x)n+1F′(x)
懒得抄了,自己看command_block的博客吧
通常来讲, H ( x ) H(x) H(x)是自己构造的。求复合逆没有比较好的方法,一般要根据题目特殊性质来。一般来讲根据 H ( x ) H(x) H(x)和 F ( x ) F(x) F(x)谁的导函数比较简单来选取公式,并且显然我们也可以看出当 n = 0 n=0 n=0时只能选后面那一种公式。
比较经典的应用是有标号有根树计数。
Part 2
咕了。自己看大佬写的题解吧。感觉肯定比我写得好。
代码:
//我还真写了,居然能过。
相关文章:
)
【学习笔记】CF1349F2 Slime and Sequences (Hard Version)
多项式工业警告!!! 点击看题意 思路来自 这位大佬 。 为什么这么好的题解没人评论。 Part 1 前置知识:拉格朗日反演(多项式复合),分式域(引入负整数次项)。 条件&a…...
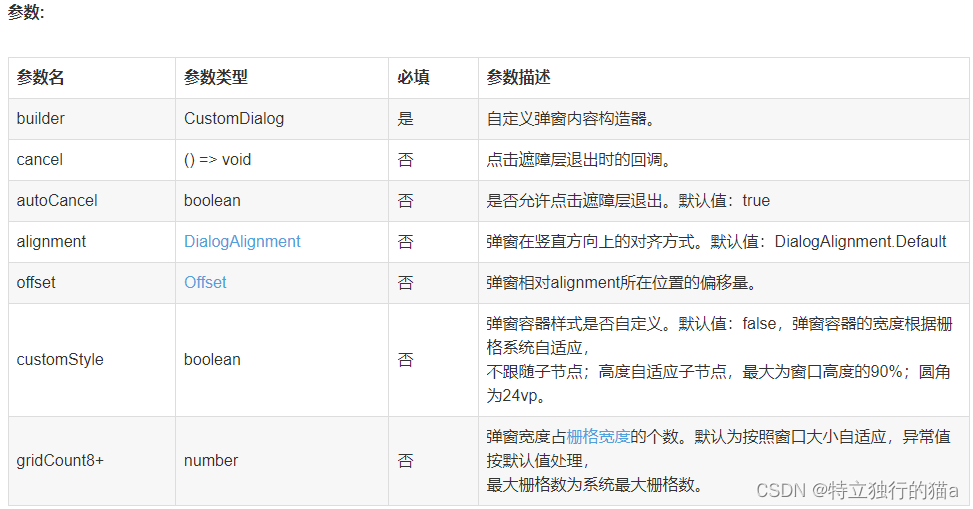
HarmonyOS 鸿蒙应用开发( 六、实现自定义弹窗CustomDialog)
自定义弹窗(CustomDialog)可用于广告、中奖、警告、软件更新等与用户交互响应操作。开发者可以通过CustomDialogController类显示自定义弹窗。具体用法请参考自定义弹窗。 在应用的使用和开发中,弹窗是一个很常见的场景,自定义弹窗…...
FileChannel)
# Java NIO(一)FileChannel
Java NIO 1.BIO与NIO的区别 BIO为阻塞IO,NIO为非阻塞IO。 BIONIOJAVA1.4之前Java 1.4之后面向流:以byte为单位处理数据面向块:以块为单位处理数据同步阻塞同步非阻塞无选择器(Selector) 1.1NIO的核心组成部分 Cha…...

[嵌入式软件][启蒙篇][仿真平台] STM32F103实现串口输出输入、ADC采集
上一篇:[嵌入式软件][启蒙篇][仿真平台] STM32F103实现LED、按键 文章目录 一、串口输出(1) 简介(2) 示例代码(3) 仿真效果 二、串口输入(1) 简介(2) 示例代码(3) 仿真效果 三、ADC采集(1) 简介(2) 采集电压(3) 示例代码(电压)(4) 仿真效果 …...

Deepin基本环境查看(四)【硬盘/分区、文件系统、硬连接/软连接】
Linux操作系统(Deepin、Ubuntu)操作系统中,硬盘分区的管理与Windows操作系统不同; 在Linux系统中维护着一个统一的文件目录体系,而硬盘和分区是以资源的形式由操作系统挂接和调度;此外Linux系统中连接(硬连…...
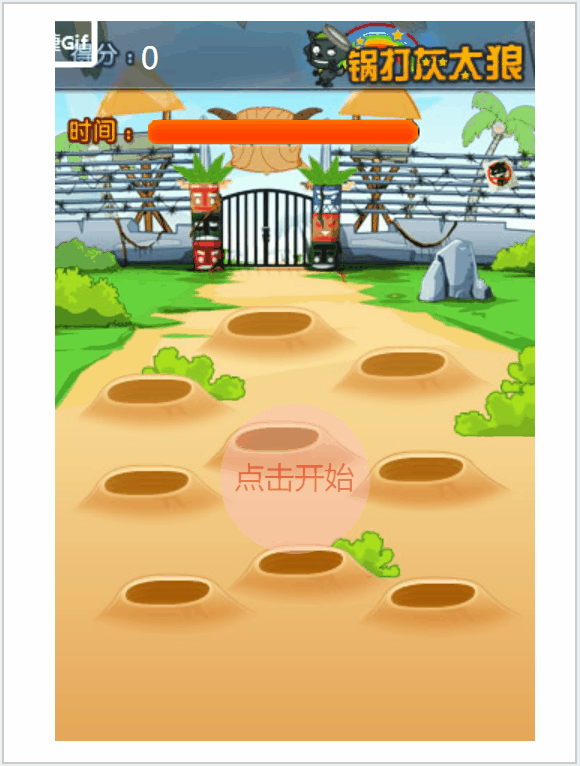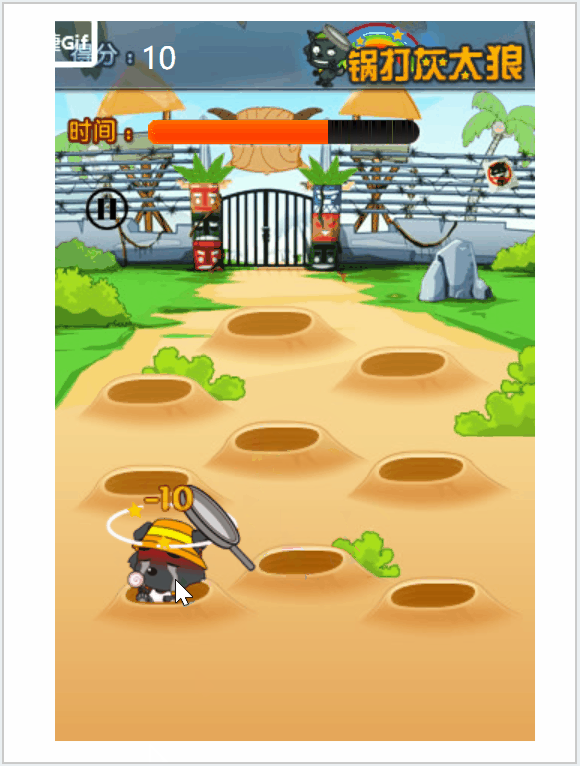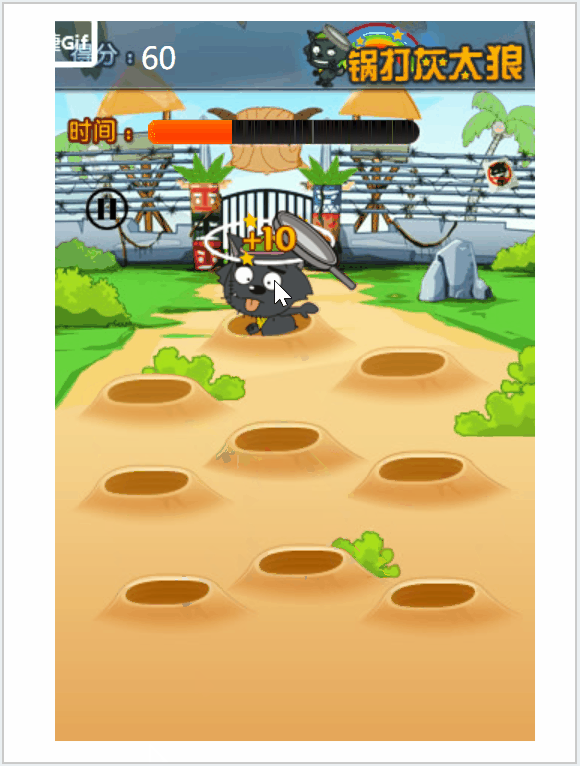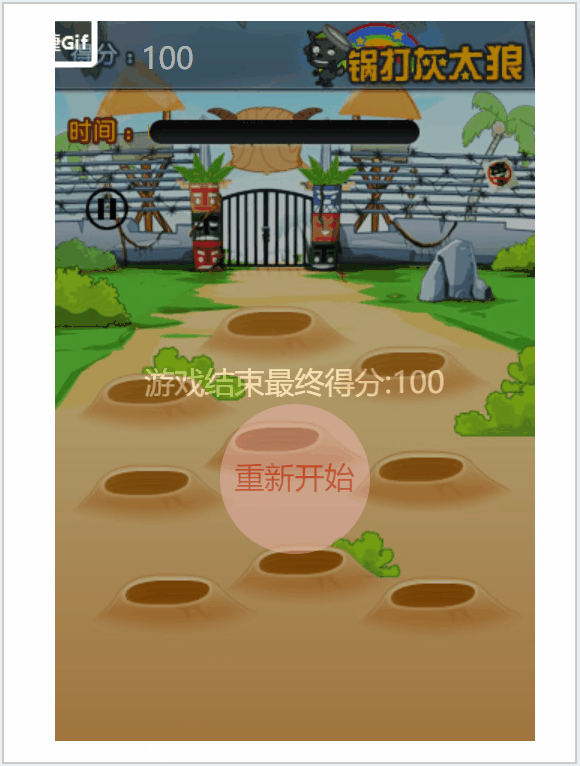
JS之打地鼠案例
需要素材的同学可以私信我 效果图: 上代码: <!DOCTYPE html> <html> <head><meta charset"utf-8"><title></title><style>* {margin: 0;padding: 0;}.box {position: relative;width: 320px;heigh…...

Kubernetes入门
k8s相关基础知识 文章目录 k8s相关基础知识1、Container2、PodPod 与 Container 的不同Pod 其它命令 3、Deployment扩容升级版本Rolling update(滚动更新)存活探针(livenessProb)就绪探针(readiness) 4、ServiceClusterIPNodePortLoadBalancer 5、Ingres…...

EtherNet/IP开发:C++搭建基础模块,EtherNet/IP源代码
这里是CIP资料的协议层级图,讲解协议构造。 ODVA(www.ODVA.org)成立于1995年,是一个全球性协会,其成员包括世界领先的自动化公司。结合其成员的支持,ODVA的使命是在工业自动化中推进开放、可互操作的信息和…...

Django(九)
1. 用户登录-Cookie和Session 什么是cookie和session? 发送HTTP请求或者HTTPS请求(无状态&短连接) http://127.0.0.1:8000/admin/list/ https://127.0.0.1:8000/admin/list/http无状态短连接:一次请求响应之后断开连接,再发请求重新连…...
)
解决Android Studio Unexpected tokens (use ; to separate expressions on the same line)
[TOC](Unexpected tokens (use ; to separate expressions on the same line)) 问题描述:Unexpected tokens (use ; to separate expressions on the same line) 原因:Android Studio 更新到最新的版本之后,gradle工程目录结构发生改变 问…...
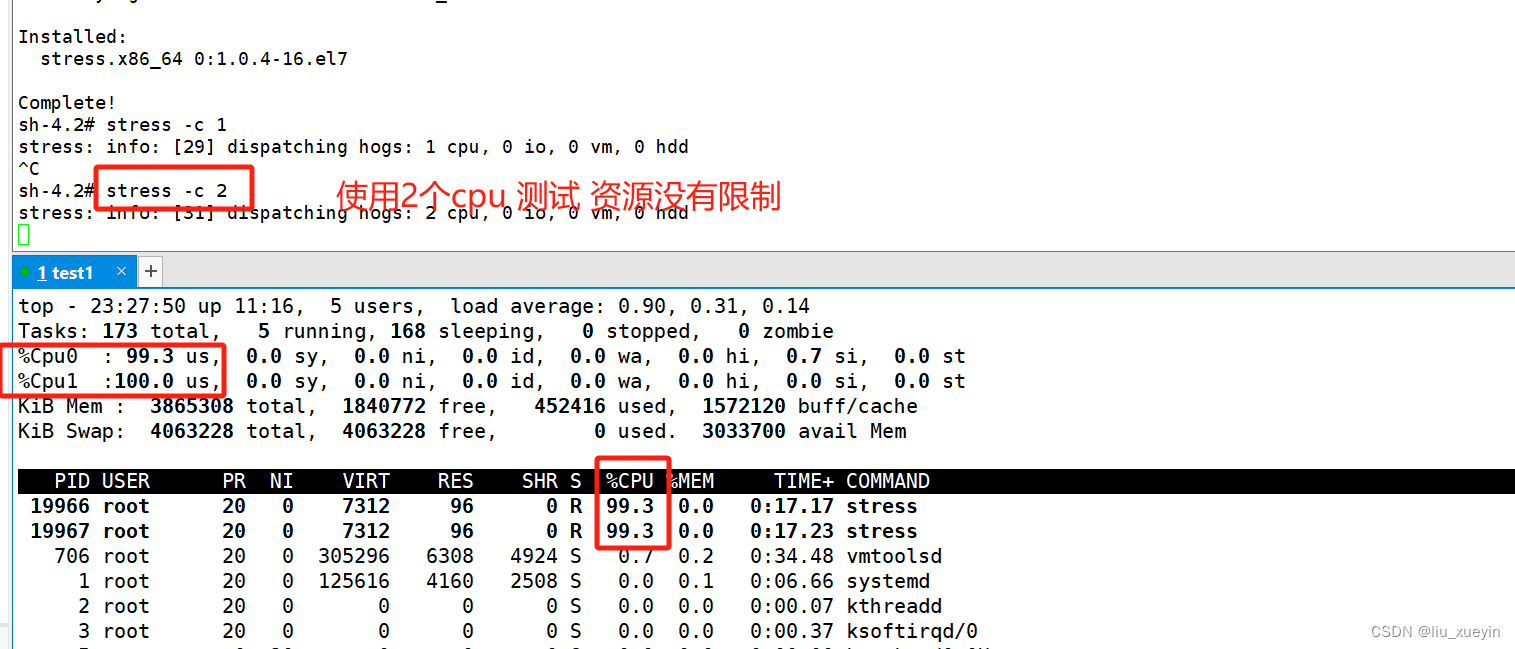
【云原生】Docker网络模式和Cgroup资源限制
目录 一、Docker 网络实现原理 二、Docker 的网络模式 #网络模式详解: 第一种:host模式 第二种:bridge模式 第三种:container模式 第四种:none模式 第五种:自定义网络 三、Cgroup资源控制 第一种&a…...

实战:加密传输数据解密
前言 下面将分享一些实际的渗透测试经验,帮助你应对在测试中遇到的数据包内容加密的情况。我们将以实战为主,技巧为辅,进入逆向的大门。 技巧 开局先讲一下技巧,掌握好了技巧,方便逆向的时候可以更加快速的找到关键…...
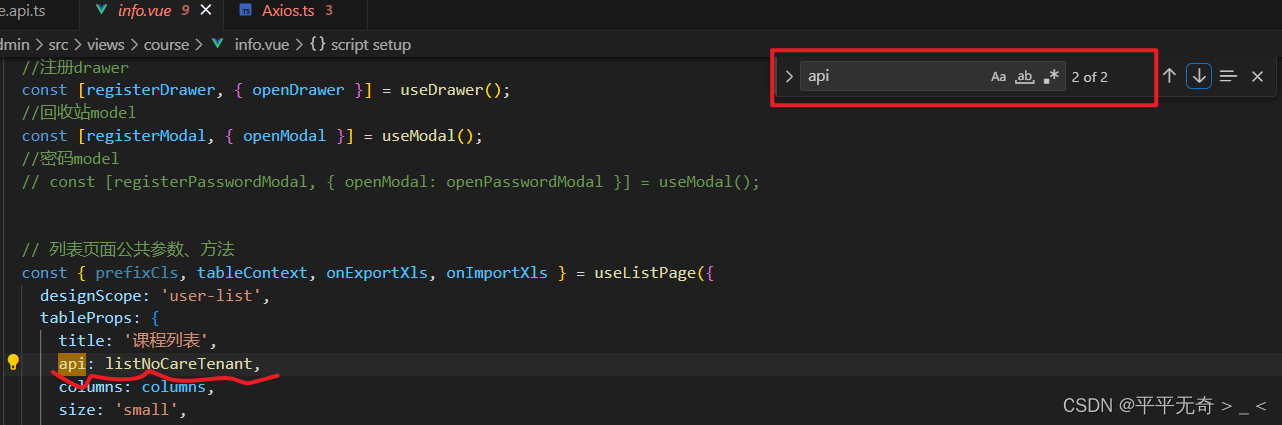
前端开发提高效率的两大工具
一、浏览器中的开发者工具 怎么启动开发者工具? 在浏览器中按下F12或者鼠标右键点击检查 怎么利用(常用的几点)? 1、元素 点击标红的图标可以用于在页面选择元素,同时右侧会找到元素在前端代码中的位置 点击下方红…...
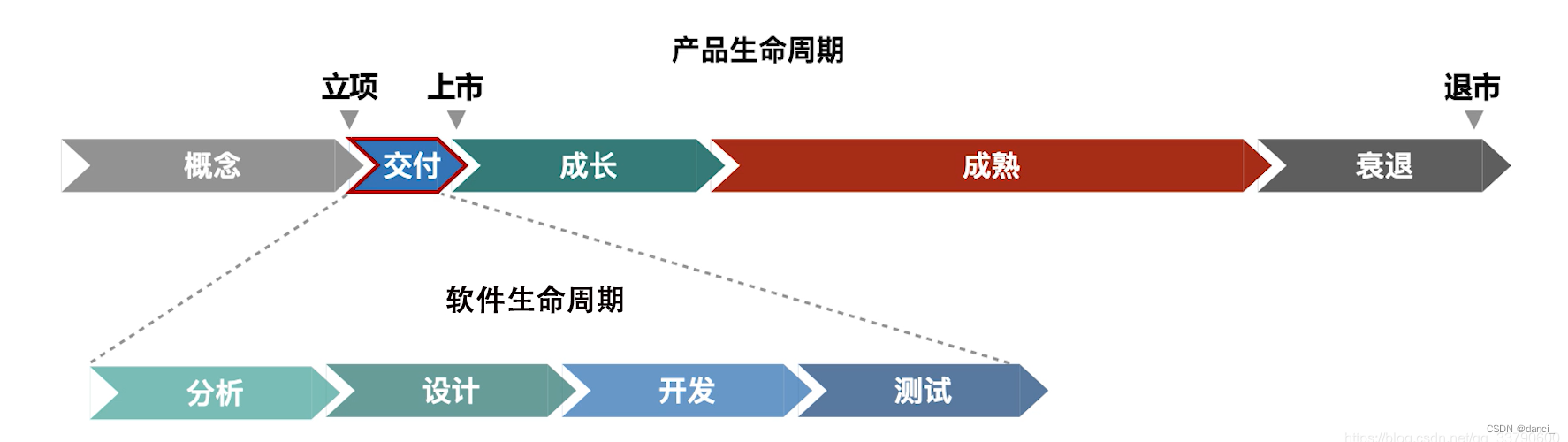
探索设计模式的魅力:深入理解面向对象设计的深层原则与思维
如何同时提高一个软件系统的可维护性 和 可复用性是面向对象对象要解决的核心问题。 通过学习和应用设计模式,可以更加深入地理解面向对象的设计理念,从而帮助设计师改善自己的系统设计。但是,设计模式并不能够提供具有普遍性的设计指导原则。…...
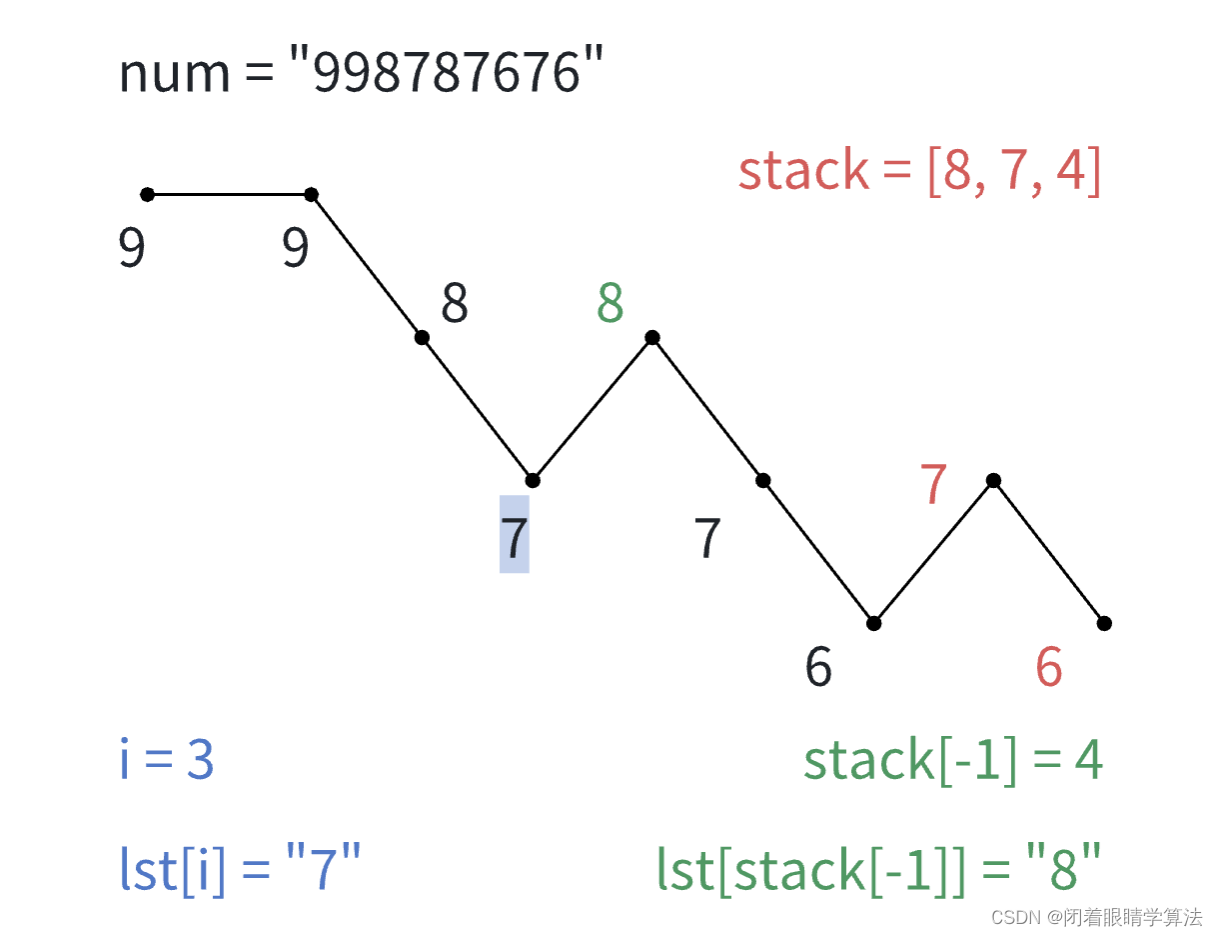
【Py/Java/C++三种语言详解】LeetCode每日一题240122【贪心】LeetCode670、最大交换
文章目录 题目链接题目描述解题思路为什么是贪心一个带图的例子 代码pythonjavacpp时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 题目链接 LeetCode670、最大交换 题目描述 给定一个非负整数数组 nums 和一个整数 k ,你需要将这个数组分成 k 个非空的连…...
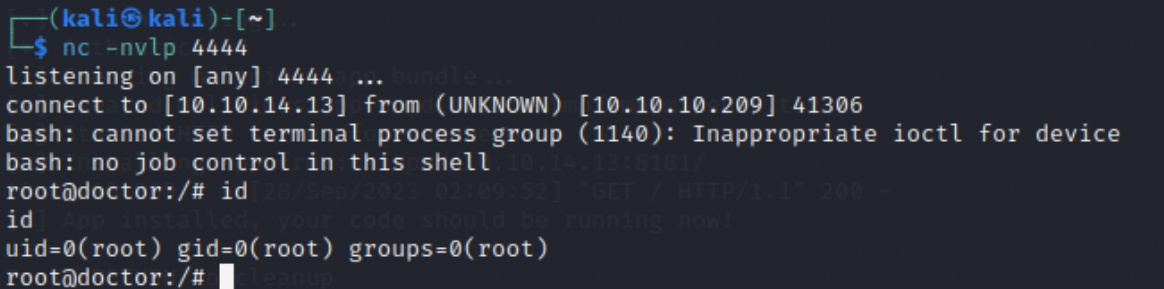
Linux/Doctor
Enumeration nmap 已知目标开放了22,80,8089端口,扫描详细情况如下 可以看到对外开放了22,80,8089三个端口 TCP/80 SSTI 访问80端口,有一个infodoctors.htb的电子邮件,点击其他的也没有什么反应,猜测有可能需要域名访问 在/et…...
嵌入式linux学习之系统烧录
1.所需文件 1. 开发板为正点原子stm32mp157,文件可按照linux驱动教程编译,也可在正点原子文档->08、系统镜像\02、出厂系统镜像中找到: 2.烧录 1.拨码开关为000(usb启动),otg接口接入虚拟机,打开stm32cubeProgrammer: 2.页面…...
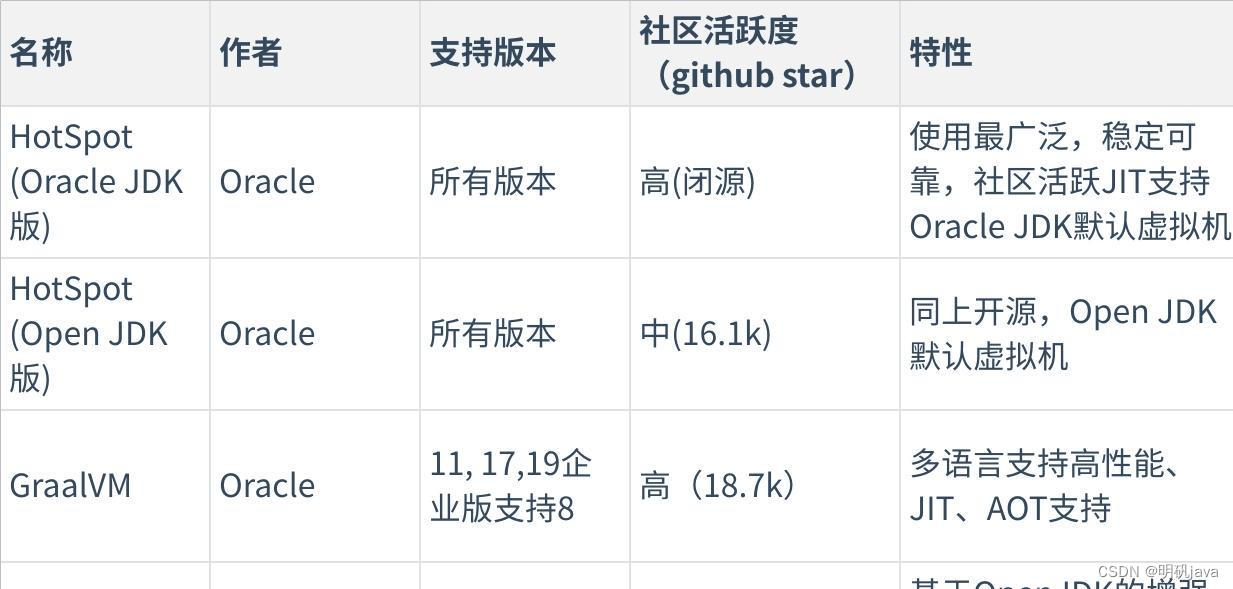
JVM-初始JVM
什么是JVM JVM 全称是 Java Virtual Machine,中文译名 Java虚拟机。JVM 本质上是一个运行在计算机上的程序,他的职责是运行Java字节码文件。 Java源代码执行流程如下: JVM的功能 1 - 解释和运行 2 - 内存管理 3 - 即时编译 解释和运行 解释…...

EXCEL VBA网抓技巧-复制网页表格,不用遍历单元格
EXCEL VBA网抓技巧-复制网页表格,不用遍历单元格 对应表格复制 Sub tableTest()Set winhttp CreateObject("winhttp.WinHttpRequest.5.1")Set HTML CreateObject("htmlfile")Set oWindow HTML.ParentWindowUrl "https://www.taiwanlo…...

动态规划——炮兵回城【集训笔记】
题目描述 游戏盘面是一个m行n列的方格矩阵,将每个方格用坐标表示,行坐标从下到上依次递增,列坐标从左至右依次递增,左下角方格的坐标为(1,1),则右上角方格的坐标为(m,n)。 游戏结束盘上只剩下一枚炮兵没有回到城池中&a…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
