算法36:单调栈结构、子数组最小乘积的最大值问题(力扣1586)----单调栈
单调栈:就是在栈中实现数据的单调性。即从栈底到栈顶,要么递增,要么递减。
那么,使用单调栈,可以解决什么问题呢?
给定一个可能含有重复值的数组arr,i位置的数一定存在如下两个信息
1)arr[i]的左侧离i最近并且小于(或者大于)arr[i]的数在哪?
2)arr[i]的右侧离i最近并且小于(或者大于)arr[i]的数在哪? 如果想得到arr中所有位置的两个信息,怎么能让得到信息的过程尽量快
题目一:给定一个一维数组,数据都为正整数并且无重复值,要求设计一个O(N)时间复杂度的算法,找出任意位置的数据,左侧小于当前位置最近的数在哪,右侧小于当前数最近的的数在哪?
假设: 这个数组是 {1,3,5,4}。栈的单调性从栈底到栈顶递增。
那么如下:
| 5 |
| 3 |
| 1 |
也就是说,前3个数符合预期的栈的单调性,可以正常的放入栈中。那么,当最后一个数据4想要放入栈中的时候,发现栈顶元素为5,比自己大。直接放入就破坏了栈的单调性了。
1. 我们需要把栈顶元素5弹出,这5就知道右侧小于自己的并且距离最近的数为4,而左侧离自己最近并且小于自己的数为3.
2. 此时,栈顶元素为3,小于4. 那么4直接放入栈顶。整个数组全部结束
| 4 |
| 3 |
| 1 |
3. 栈循环弹出,4是最后一个元素,并且栈具有单调性。因此,弹出4可以知道,左侧离自己最近的数为3. 而右侧没有比自己更小的数
4. 弹出3,左侧比自己小的数是1,而右侧没有比自己小的数
5. 弹出1,此时栈空了。左侧、右侧都没有小于自己的数。
以上一切,只是为了直观的体现栈整个操作流程。而实际的算法设计肯定是不能用数据来直接使用的,而是需要使用每个数据对应的位置,即下标
//无重复元素public int[][] dp(int[] arr){if(arr == null || arr.length == 0) {return null;}int[][] dp = new int[arr.length][arr.length];Stack<Integer> stack = new Stack<>();for (int i = 0; i < arr.length; i++){while (!stack.isEmpty() && arr[stack.peek()] > arr[i]){int cur = stack.pop();// -1代表不存在左侧比cur下标对应的值更小的值int leftIndex = stack.isEmpty() ? -1 : stack.peek();dp[cur][0] = leftIndex;dp[cur][1] = i;}//放入下标stack.push(i);}//栈中剩余元素,保持单调增while (!stack.isEmpty()) {int cur = stack.pop();// -1代表不存在左侧比cur下标对应的值更小的值int leftIndex = stack.isEmpty() ? -1 : stack.peek();dp[cur][0] = leftIndex;//因为单调增、所有右侧不存在比自己还小的值了dp[cur][1] = -1;}return dp;}
题目二:数组存在重复元素,设计一个栈,要求能够快速找到任意位置左、右侧比自己小、位置最近的数据。
public static int[][] getNearLess(int[] arr) {int[][] res = new int[arr.length][2];Stack<List<Integer>> stack = new Stack<>();for (int i = 0; i < arr.length; i++) { // i -> arr[i] 进栈while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {List<Integer> popIs = stack.pop();int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);for (Integer popi : popIs) {res[popi][0] = leftLessIndex;res[popi][1] = i;}}if (!stack.isEmpty() && arr[stack.peek().get(0)] == arr[i]) {stack.peek().add(Integer.valueOf(i));} else {ArrayList<Integer> list = new ArrayList<>();list.add(i);stack.push(list);}}while (!stack.isEmpty()) {List<Integer> popIs = stack.pop();int leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);for (Integer popi : popIs) {res[popi][0] = leftLessIndex;res[popi][1] = -1;}}return res;}题目三:力扣1856. 子数组最小乘积的最大值
https://leetcode.cn/problems/maximum-subarray-min-product/description/
题目详情直接打开连接进行查看,这里直接说解题思路。
1. 给定数组,就存在子数组,并且子数组是连续的
2.子数组中肯定是存在最小值的,也必然会知道子数组累加和。
3. 假设每个数都是最小值,这样就能利用单调栈结构找到左侧、右侧比自己小的位置。那么除了这两个位置以外,中间部分的数据就是自己最小了。利用这个思想,我们来实现代码
| 数据 | 1 | 3 | 5 | 4 |
| 下标 | 0 | 1 | 2 | 3 |
| 累加和 | 1 | 4 | 9 | 13 |
5左侧比自己小的数据为3,对应下标为1;
5右侧比自己小的数据为4,对应下标为3;
也就是说5这个数据想要做最小值,那么下标1到3之间,并且不能包含下标1和下标3的和。
既然不能包含到下标为3的位置,变相的也就是能够包含到下标为2的位置,即累加和为 9 - 4 = 5;
那子数组累加和 * 最小值 = 5 * 5 = 25;
其他的依次类推........
package code04.单调栈_01;import java.util.Stack;/*** 1856. 子数组最小乘积的最大值* https://leetcode.cn/problems/maximum-subarray-min-product/description/*/
public class Code01_MinSumOfSubArr {public int maxSumMinProduct(int[] nums){if (nums == null || nums.length == 0) {return 0;}int size = nums.length;//前缀和数组。 题目规定要使用64位有符号整数保存long[] dp = new long[size];dp[0] = nums[0];for (int i = 1; i < size; i++) {dp[i] = dp[i-1] + nums[i];}long ans = Long.MIN_VALUE;//[0 ......)Stack<Integer> stack = new Stack();for(int i = 0; i < size; i++){while (!stack.isEmpty()&& nums[stack.peek()] >= nums[i]) {//当前正在处理的数下标int cur = stack.pop();long sum = stack.isEmpty() ? dp[i-1] : dp[i-1] - dp[stack.peek()];ans = Math.max(ans, sum * nums[cur]);}//放入下标stack.push(i);}//右侧值越来越大while (!stack.isEmpty()) {//当前正在处理的数下标int cur = stack.pop();long sum = stack.isEmpty() ? dp[size-1] : (dp[size-1] - dp[stack.peek()]);ans = Math.max(ans, sum * nums[cur]);}return (int) (ans % 1000000007);}public static void main(String[] args){int[] nums = {3,1,5,6,4,2};Code01_MinSumOfSubArr test = new Code01_MinSumOfSubArr();System.out.println(test.maxSumMinProduct(nums));}
}
此处可能会有疑问,此处使用的是无重复元素构造单调栈的算法,这一题不需要考虑重复元素的情况吗?举个例子,假如数组为 {1,2,3,2}
栈中放入1,2 3. 当放入最后一个2的时候,会把栈中的3和2弹出,并且把最后一个2入栈。 而最后一个2右侧没有比他小的值,左侧比他小的值为1,对应的下标为0. 也就是说从下标0到最后一个2的位置,此时最后一个2是最小值。当然,下标0处的1是不包含在内的。
也就是说,重复元素具有连通性,很多时候是不需要考虑重复元素的情况的。
相关文章:
----单调栈)
算法36:单调栈结构、子数组最小乘积的最大值问题(力扣1586)----单调栈
单调栈:就是在栈中实现数据的单调性。即从栈底到栈顶,要么递增,要么递减。 那么,使用单调栈,可以解决什么问题呢? 给定一个可能含有重复值的数组arr,i位置的数一定存在如下两个信息 1&#x…...

django mysql in 有序返回
from django.db.models import * ordering f"FIELD(id, {,.join([str(_) for _ in ids])})" # 默认就按照算法返回的 id 排序p_data_result PeptidesDataResult.objects.using("polypeptide").filter(id__inids).values().extra(select{ordering: orderi…...

c++24.1.26嵌套if语句
嵌套if语句:if语句中的if语句 实践:...
)
机器学习--基础概念(二)
1.分类算法 分类算法是有监督学习的一个核心问题,他从数据中学习一个分类决策函数或分类模型,对新的输入进行预测,输出变量取有限个离散值。 以下是一些常见的分类算法: 逻辑回归 (Logistic Regression): 用于二分类问题&#x…...
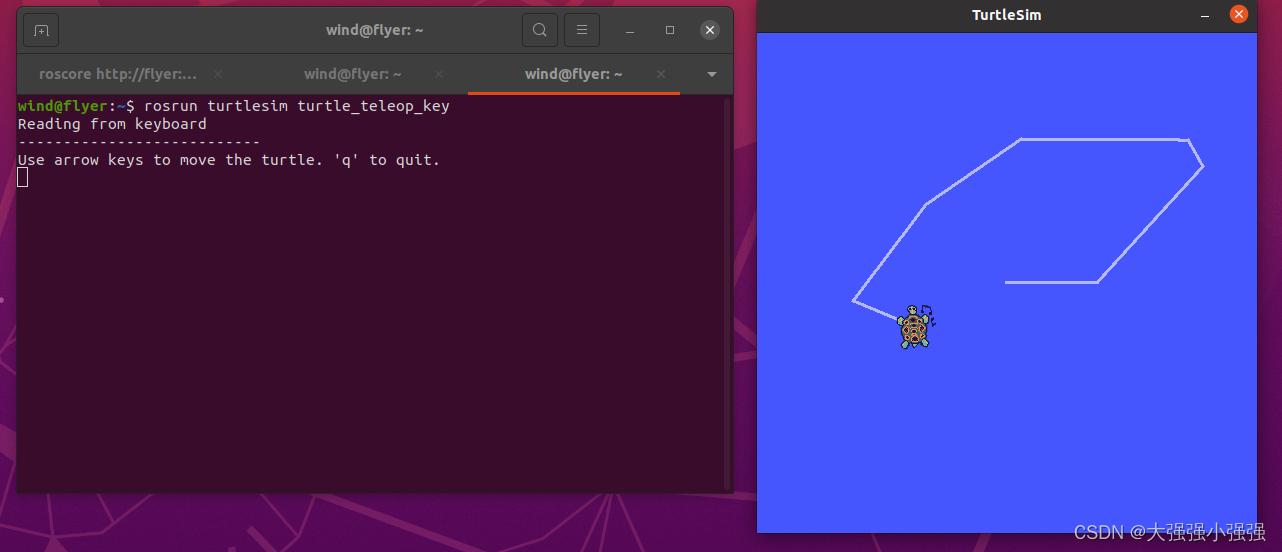
Ubuntu20.04 安装 ROS noetic + MAVROS
本文在 AlphaCatOvO【ROS】在 Ubuntu 20.04 安装 ROS 的详细教程 基础上,根据实际安装经验,稍微进行补充。 一、安装Ubuntu20.04 假设已经正确安装。 二、安装 ROS noetic 2.1 换源 执行 sudo apt update sudo mv /etc/apt/sources.list /etc/apt/…...

【数学笔记】一元n次不等式,分式不等式,绝对值不等式
不等式 基本性质 一元n次不等式一元二次不等式一元高次不等式分式不等式绝对值不等式 基本性质 性质 a > b ⇔ b < a a>b\Leftrightarrow b<a a>b⇔b<a a > b , b > c ⇒ a > c a>b,b>c\Rightarrow a>c a>b,b>c⇒a>c a > b ,…...

转载-android性能优化
android性能优化 Reason: Broadcast of Intent { actandroid.intent.action.TIME_TICK ActivityManager: ANR in com.***.*** PID: 16227 Reason: Broadcast of Intent { actandroid.intent.action.TIME_TICK flg0x50000014 (has extras) }有那么一段时间我被这个ANR折磨到每…...

笔记 | Clickhouse命令行查询
在 ClickHouse 中,可以使用命令行客户端执行查询。默认情况下,ClickHouse 的命令行客户端称为 clickhouse-client。下面是一些基本的步骤和示例,用于使用 clickhouse-client 进行查询。 首先,需要确保已经安装了 ClickHouse 服务…...

Dockerfile-xxxx
1、Dockerfile-server FROM openjdk:8-jdk-alpine WORKDIR /app COPY . . CMD java -Xms1536M -Xmx1536M -XX:UseG1GC -jar -Dlog4j2.formatMsgNoLookupstrue -Dloader.pathresources,lib -Duser.timezoneGMT-05 /app/server-main-1.0.0.jar 2、Dockerfile-bgd #FROM openjdk…...

Vue中的$attrs
今天产品经理要求做保留某组件全部功能,还要在它的基础上增加东西。如果不嫌麻烦的话就笨办法,但是想一下怎么只用少量代码高效的二次封装组件呢 Vue中的$attrs 在 Vue2 中,attr 是指组件接收的 HTML 特性(attribute),通过 prop…...

使用阿里云的oss对象存储服务实现图片上传(前端vue后端java详解)
一:前期准备: 1.1:注册阿里云账号,开启对象存储oss功能,创建一个bucket(百度教程多的是,跟着创建一个就行,创建时注意存储类型是标准存储,读写权限是公共读)…...

python实例100第32例:使用a[::-1]按相反的顺序输出列表的值
题目:按相反的顺序输出列表的值。 程序分析: a[n:-n]作用是去除前n个元素和末n个元素a[-n]作用是取倒数第n个元素a[:-n]的作用是去除后n个元素a[::-1]的作用是将所有元素逆序排列a[n::-1] 的作用是从第n个元素截取后逆序排列 程序…...

python执行脚本的时候获取输入参数
当我们执行脚本的时候,通常都会执行 python test.py -i xxx -o xxx,这里的 -i 和 -o 都是输入参数,这到底是怎么传递的呢? 本文纯粹记录一下 import argparseif __name__ __main__:print("hello")# 创建AugumentParser…...

Halcon指定区域的形状匹配
Halcon指定区域的形状匹配 文章目录 Halcon指定区域的形状匹配1.在参考图像中选择目标2.创建模板3.搜索目标 在这个实例中,会介绍如何根据选定的ROI选择合适的图像金字塔参数,创建包含这个区域的形状模板,并进行精确的基于形状模板的匹配。最…...
Linux——常用命令
1、命令的基本格式 对服务器来讲,图形界面会占用更多的系统资源,而且会安装更多的服务、开放更多的端口,这对服务器的稳定性和安全性都有负面影响。其实,服务器是一个连显示器都没有的家伙,要图形界面干什么ÿ…...
外包干了2个月,技术反而退步了...
先说一下自己的情况,本科生,19年通过校招进入广州某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
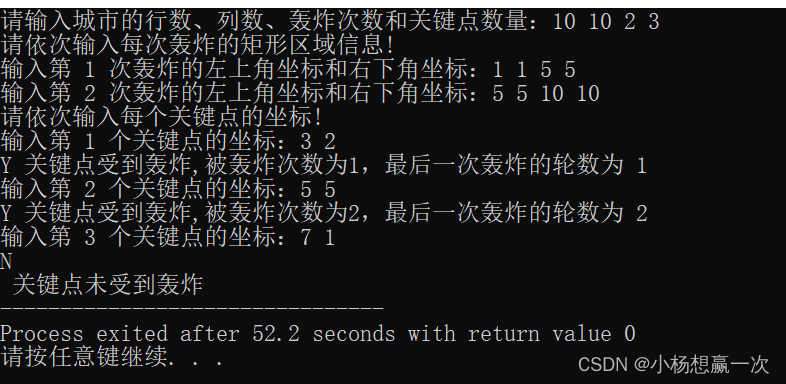
洛谷C++简单题练习day6—P1830 城市轰炸
day6--P1830 城市轰炸--1.26 习题概述 题目背景 一个大小为 nm 的城市遭到了 x 次轰炸,每次都炸了一个每条边都与边界平行的矩形。 题目描述 在轰炸后,有 y 个关键点,指挥官想知道,它们有没有受到过轰炸,如果有&a…...

【linux-interconnect】What NVIDIA MLNX_OFED is?
NVIDIA MLNX_OFED Documentation v23.07 - NVIDIA Docs 文章目录 What NVIDIA MLNX_OFED is?Overview[Software Download](https://docs.nvidia.com/networking/display/mlnxofedv23070512#src-2396583107_NVIDIAMLNX_OFEDDocumentationv23.07-SoftwareDownload) Wh…...

Unity开发中的XML注释
在Unity开发中,XML注释主要用于C#脚本的注释,以帮助生成代码文档和提供IntelliSense功能。以下是一些关于如何使用XML注释的技巧: 创建注释: 在C#中,XML注释是由///或/**...*/开始的。例如 /// <summary> /// 这…...

[MQ]常用的mq产品图形管理web界面或客户端
一、MQ介绍 1.1 定义 MQ全称为Message Queue,消息队列是应用程序和应用程序之间的通信方法。 如果非要用一个定义来概括只能是抽象出来一些概念,概括为跨服务之间传递信息的软件。 1.2 MQ产品 较为成熟的MQ产品:IBMMQ(IBM We…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
