深度强化学习(王树森)笔记02
深度强化学习(DRL)
本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。
参考链接
Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL
源代码链接:https://github.com/DeepRLChinese/DeepRL-Chinese
B站视频:【王树森】深度强化学习(DRL)
豆瓣: 深度强化学习
文章目录
- 深度强化学习(DRL)
- Value-based RL
- DQN
- 时间差分(TD)算法
- 驾车时间预测的例子
- TD算法
- 用TD训练DQN
- 注意
- 后记
Value-based RL
DQN
在学习 DQN之前,首先复习一些基础知识。在一局游戏中,把从起始到结束的所有奖励记作:
R 1 , ⋯ , R t , ⋯ , R n . R_{1},\cdots,R_{t},\cdots,R_{n}. R1,⋯,Rt,⋯,Rn.
定义折扣率 γ ∈ [ 0 , 1 ] \gamma\in[0,1] γ∈[0,1]。折扣回报的定义是:
U t = R t + γ ⋅ R t + 1 + γ 2 ⋅ R t + 2 + ⋯ + γ n − t ⋅ R n . U_{t}\:=\:R_{t}+\gamma\cdot R_{t+1}+\gamma^{2}\cdot R_{t+2}+\cdots+\gamma^{n-t}\cdot R_{n}. Ut=Rt+γ⋅Rt+1+γ2⋅Rt+2+⋯+γn−t⋅Rn.
在游戏尚未结束的 t t t 时刻, U t U_t Ut 是一个未知的随机变量,其随机性来自于 t t t 时刻之后的所有状态与动作。动作价值函数的定义是:
Q π ( s t , a t ) = E [ U t ∣ S t = s t , A t = a t ] , Q_{\pi}(s_{t},a_{t})\:=\:\mathbb{E}\Big[U_{t}\Big|\:S_{t}=s_{t},A_{t}=a_{t}\Big], Qπ(st,at)=E[Ut St=st,At=at],
公式中的期望消除了 t t t 时刻之后的所有状态 S t + 1 , ⋯ , S n S_{t+1},\cdots,S_n St+1,⋯,Sn 与所有动作 A t + 1 , ⋯ , A n A_{t+1},\cdots,A_n At+1,⋯,An。

最优动作价值函数用最大化消除策略 π : \pi: π:
Q ⋆ ( s t , a t ) = max π Q π ( s t , a t ) , ∀ s t ∈ S , a t ∈ A . Q_{\star}\big(s_{t},a_{t}\big)\:=\:\max_{\pi}\:Q_{\pi}\big(s_{t},a_{t}\big),\quad\forall\:s_{t}\in\mathcal{S},\quad a_{t}\in\mathcal{A}. Q⋆(st,at)=πmaxQπ(st,at),∀st∈S,at∈A.
可以这样理解 Q ⋆ : Q_\star : Q⋆:已知 s t s_t st和 a t a_t at,不论未来采取什么样的策略 π \pi π,回报 U t U_t Ut的期望不可能超过 Q ⋆ ∘ Q_{\star\circ} Q⋆∘

最优动作价值函数的用途:假如我们知道 Q ⋆ Q_\star Q⋆,我们就能用它做控制。举个例子,超级玛丽游戏中的动作空间是 A = { 左,右,上 } A= \{ 左,右,上\} A={左,右,上}。给定当前状态 s t s_t st,智能体该执行哪个动作呢?假设我们已知 Q ⋆ Q_{\star} Q⋆函数,那么我们就让 Q ⋆ Q_{\star} Q⋆给三个动作打分,比如:
Q ⋆ ( s t , 左 ) = 370 , Q ⋆ ( s t , 右 ) = − 21 , Q ⋆ ( s t , 上 ) = 610. Q_{\star}(s_{t},\textit{左})\:=\:370,\quad Q_{\star}(s_{t},\textit{右})\:=\:-21,\quad Q_{\star}(s_{t},\text{上})\:=\:610. Q⋆(st,左)=370,Q⋆(st,右)=−21,Q⋆(st,上)=610.
这三个值是什么意思呢? Q ⋆ ( s t , 左 ) = 370 Q_\star ( s_t, 左) = 370 Q⋆(st,左)=370 的意思是:如果现在智能体选择向左走,不论之后采取什么策略 π, 那么回报 U t U_t Ut 的期望最多不会超过 370。同理,其他两个最优动作价值也是回报的期望的上界。根据 Q ⋆ Q_{\star} Q⋆的评分,智能体应该选择向上跳,因为这样可以最大化回报 U t U_t Ut 的期望。
我们希望知道 Q ⋆ Q_{\star} Q⋆,因为它就像是先知一般,可以预见未来,在 t t t 时刻就预见 t t t到 n n n 时刻之间的累计奖励的期望。假如我们有 Q ⋆ Q_{\star} Q⋆这位先知,我们就遵照先知的指导,最大化未来的累计奖励。然而在实践中我们不知道 Q ⋆ Q_{\star} Q⋆的函数表达式。是否有可能近似出 Q ⋆ Q_{\star} Q⋆这位先知呢?对于超级玛丽这样的游戏,学出来一个“先知”并不难。假如让我们重复玩超级玛丽一亿次,那我们就会像先知一样,看到当前状态,就能准确判断出当前最优的动作是什么。这说明只要有足够多的“经验”,就能训练出超级玛丽中的“先知”。

最优动作价值函数的近似:在实践中,近似学习“先知” Q ⋆ Q_{\star} Q⋆ 最有效的办法是深度 Q网络(deep Q network, 缩写 DQN), 记作 Q ( s , a ; w ) Q(s,a;\boldsymbol{w}) Q(s,a;w), 其结构如图 4.1 所述。其中的 w w w 表示神经网络中的参数。首先随机初始化 w w w,随后用“经验”去学习 w w w。学习的目标是:对于所有的 s s s 和 a a a, DQN 的预测 Q ( s , a ; w ) Q(s,a;\boldsymbol{w}) Q(s,a;w)尽量接近 Q ⋆ ( s , a ) Q_\star(s,a) Q⋆(s,a)。后面几节的内容都是如何学习 w w w
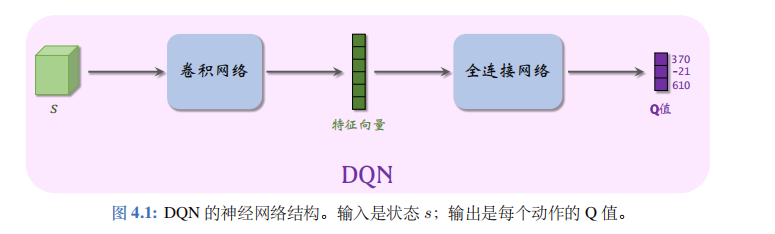
可以这样理解 DQN 的表达式 Q ( s , a ; w ) Q(s,a;\boldsymbol{w}) Q(s,a;w)。DQN 的输出是离散动作空间 A A A 上的每个动作的 Q 值,即给每个动作的评分,分数越高意味着动作越好。举个例子,动作空间是 A = { 左,右,上 } \mathcal{A} = \{ 左,右,上\} A={左,右,上},那么动作空间的大小等于 ∣ A ∣ = 3 |\mathcal{A}|=3 ∣A∣=3,那么 DQN 的输出是 3 维的向量, 记作 q ^ \widehat{q} q , 向量每个元素对应一个动作。在图4.1 中,DQN 的输出是
q ^ 1 = Q ( s , 左 ; w ) = 370 , q ^ 2 = Q ( s , 右 ; w ) = − 21 , q ^ 3 = Q ( s , 上 ; w ) = 610. \begin{aligned}&\widehat q_1\:=\:Q\big(s,\:\text{左};\:\boldsymbol w\big)\:=\:370,\\[1ex]&\widehat q_2\:=\:Q\big(s,\:\text{右};\:\boldsymbol w\big)\:=\:-21,\\[1ex]&\widehat q_3\:=\:Q\big(s,\:\text{上};\:\boldsymbol w\big)\:=\:610.\end{aligned} q 1=Q(s,左;w)=370,q 2=Q(s,右;w)=−21,q 3=Q(s,上;w)=610.
总结一下,DQN 的输出是 |A| 维的向量 q ^ \widehat{q} q , 包含所有动作的价值。而我们常用的符号 Q ( s , a ; w ) Q(s,a;\boldsymbol{w}) Q(s,a;w) 是标量,是动作 a a a 对应的动作价值,是向量 q ^ \hat{q} q^ 中的一个元素。
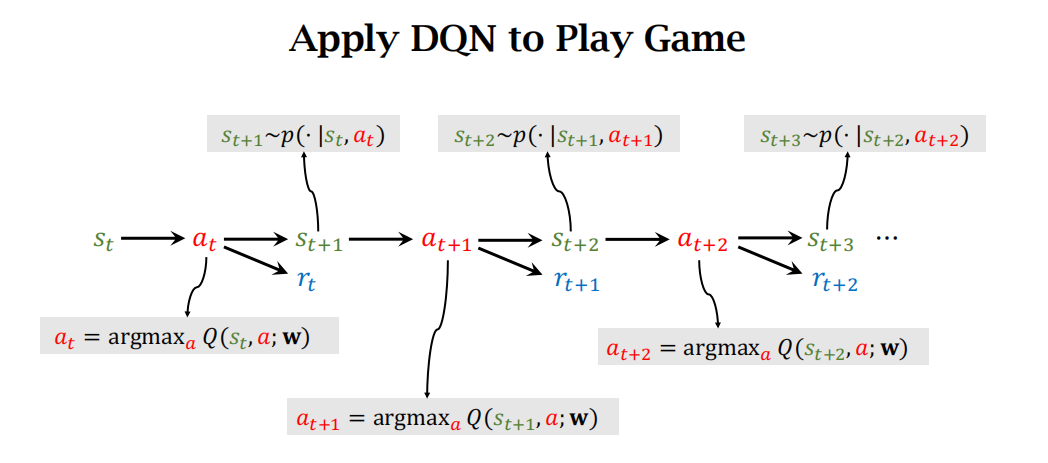
用DQN玩游戏:agent每次采取的action是使得Q函数取最大的那个动作,一直玩下去。下图的顺序是从左往右看。
DQN 的梯度:在训练 DQN 的时候,需要对 DQN 关于神经网络参数 w w w 求梯度。用
∇ w Q ( s , a ; w ) ≜ ∂ Q ( s , a ; w ) ∂ w \nabla_{\boldsymbol{w}}Q(s,a;\boldsymbol{w})\:\triangleq\:\frac{\partial\:Q(s,a;\boldsymbol{w})}{\partial\boldsymbol{w}} ∇wQ(s,a;w)≜∂w∂Q(s,a;w)
表示函数值 Q ( s , a ; w ) Q(s,a;\boldsymbol{w}) Q(s,a;w) 关于参数 w w w 的梯度。因为函数值 Q ( s , a ; w ) Q(s,a;\boldsymbol{w}) Q(s,a;w) 是一个实数,所以梯度的形状与 w w w 完全相同。如果 w w w 是 d × 1 d\times1 d×1 的向量,那么梯度也是 d × 1 d\times1 d×1 的向量。如果 w w w 是 d 1 × d 2 d_1\times d_2 d1×d2的矩阵,那么梯度也是 d 1 × d 2 d_1\times d_2 d1×d2的矩阵。如果 w w w 是 d 1 × d 2 × d 3 d_1\times d_2\times d_3 d1×d2×d3的张量,那么梯度也是 d 1 × d 2 × d 3 d_1\times d_2\times d_3 d1×d2×d3 的张量。
给定观测值 s s s 和 a a a,比如 a = 左 a=\text{左} a=左,可以用反向传播计算出梯度 ∇ w Q ( s , 左 ; w ) \nabla_{\boldsymbol{w}}Q( s, 左; \boldsymbol{w}) ∇wQ(s,左;w)。在编程实现的时候,TensorFlow 和PyTorch 可以对 DQN 输出向量的一个元素(比如 Q ( s , 左 ; w ) Q( s, 左; \boldsymbol w) Q(s,左;w) 这个元素) 关于变量 w w w 自动求梯度,得到的梯度的形状与 w w w 完全相同。
时间差分(TD)算法
驾车时间预测的例子
假设我们有一个模型 Q ( s , d ; w ) Q(s,d;w) Q(s,d;w),其中 s s s 是起点, d d d 是终点, w w w 是参数。模型 Q Q Q 可以预测开车出行的时间开销。这个模型一开始不准确,甚至是纯随机的。但是随着很多人用这个模型,得到更多数据、更多训练,这个模型就会越来越准,会像谷歌地图一样准。
我们该如何训练这个模型呢?在用户出发前,用户告诉模型起点 s s s 和终点 d d d, 模型做一个预测 q ^ = Q ( s , d ; w ) \widehat{q}=Q(s,d;w) q =Q(s,d;w)。当用户结束行程的时候,把实际驾车时间 y y y 反馈给模型。两者之差 q ^ − y \widehat{q}-y q −y 反映出模型是高估还是低估了驾驶时间,以此来修正模型,使得模型的估计更准确。
假设我是个用户,我要从北京驾车去上海。从北京出发之前,我让模型做预测,模型告诉我总车程是 14 小时:
q ^ ≜ Q ( “北京”,“上海”; w ) = 14. \widehat q\:\triangleq\:Q{({\text{“北京”,“上海”;}\boldsymbol{w})}\:=\:14.} q ≜Q(“北京”,“上海”;w)=14.
当我到达上海,我知道自己花的实际时间是16 小时,并将结果反馈给模型;见图 4.2.

可以用梯度下降对模型做一次更新,具体做法如下。把我的这次旅程作为一组训练数据:
s = “北京” , d = “上海” , q ^ = 14 , y = 16. s=\text{“北京”},\quad d=\text{“上海”},\quad\widehat{q}=14,\quad y=16. s=“北京”,d=“上海”,q =14,y=16.
我们希望估计值 q ^ = Q ( s , d ; w ) \widehat{q}=Q(s,d;\boldsymbol{w}) q =Q(s,d;w)尽量接近真实观测到的 y y y,所以用两者差的平方作为损失函数:
L ( w ) = 1 2 [ Q ( s , d ; w ) − y ] 2 . L(\boldsymbol{w})\:=\:\frac{1}{2}\Big[Q(s,d;\boldsymbol{w})\:-\:y\Big]^{2}. L(w)=21[Q(s,d;w)−y]2.
用链式法则计算损失函数的梯度,得到:
∇ w L ( w ) = ( q ^ − y ) ⋅ ∇ w Q ( s , d ; w ) , \nabla_{\boldsymbol{w}}L(\boldsymbol{w})\:=\:(\widehat{q}-y)\cdot\nabla_{\boldsymbol{w}}Q(s,d;\boldsymbol{w}), ∇wL(w)=(q −y)⋅∇wQ(s,d;w),
然后做一次梯度下降更新模型参数 w w w:
w ← w − α ⋅ ∇ w L ( w ) , w\:\leftarrow\:w-\alpha\cdot\nabla_{\boldsymbol{w}}L(\boldsymbol{w})\:, w←w−α⋅∇wL(w),
此处的 α \alpha α 是学习率,需要手动调整。在完成一次梯度下降之后,如果再让模型做一次预测,那么模型的预测值
Q ( “北京”,“上海”; w ) Q(\text{“北京”,“上海”; }w) Q(“北京”,“上海”; w)
会比原先更接近 y = 16. y=16. y=16.
TD算法
接着上文驾车时间的例子。出发前模型估计全程时间为 q ^ = 14 \widehat{q}=14 q =14 小时;模型建议的路线会途径济南。我从北京出发,过了 r = 4.5 r=4.5 r=4.5 小时,我到达济南。此时我再让横型做一次预测,模型告诉我
q ^ ′ ≜ Q ( “济南”,“上海”; w ) = 11. \widehat{q}^{\prime}\:\triangleq\:Q{({\text{“济南”,“上海”; }\boldsymbol{w}}})\:=\:11. q ′≜Q(“济南”,“上海”; w)=11.
见图 4.3 的描述。假如此时我的车坏了,必须要在济南修理,我不得不取消此次行程。我没有完成旅途,那么我的这组数据是否能帮助训练模型呢?其实是可以的,用到的算法叫做时间差分 (temporal difference, 缩写 TD)。
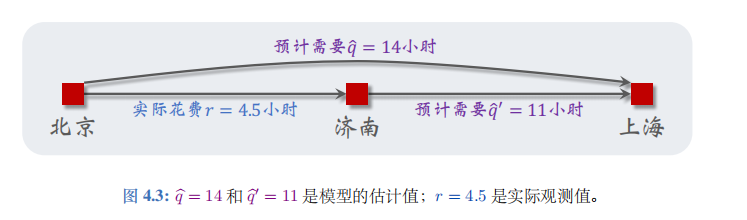
下面解释 TD 算法的原理。回顾一下我们已有的数据:模型估计从北京到上海一共需要 q ^ = 14 \widehat{q}=14 q =14 小时,我实际用了 r = 4.5 r=4.5 r=4.5 小时到达济南,模型估计还需要 q ~ ′ = 11 \widetilde{q}^{\prime}=11 q ′=11 小时从济南到上海。到达济南时,根据模型最新估计,整个旅程的总时间为:
y ^ ≜ r + q ^ ′ = 4.5 + 11 = 15.5. \widehat{y}\:\triangleq\:r+\widehat{q}^{\prime}\:=\:4.5+11\:=\:15.5. y ≜r+q ′=4.5+11=15.5.
TD 算法将 y ^ = 15.5 \widehat{y}=15.5 y =15.5 称为 TD 目标 (TD target) , 它比最初的预测 q ^ = 14 \widehat{q}=14 q =14 更可靠。最初的预测 q ^ = 14 \widehat{q}=14 q =14 纯粹是估计的,没有任何事实的成分。TD 目标 y ^ = 15.5 \widehat{y}=15.5 y =15.5 也是个估计,但其中有事实的成分:其中的 r = 4.5 r=4.5 r=4.5 就是实际的观测。
基于以上讨论,我们认为 TD 目标 y ^ = 15.5 \widehat{y}=15.5 y =15.5 比模型最初的估计值
q ^ = Q ( “北京”,“上海”; w ) = 14 \widehat{q}\:=\:Q(\text{“北京”,“上海”;}\:\boldsymbol{w})\:=\:14 q =Q(“北京”,“上海”;w)=14
更可靠,所以可以用 y ^ \hat{y} y^对模型做“修正”。我们希望估计值 q ^ \widehat{q} q 尽量接近 TD 目标 y ^ \widehat{y} y ,所以用两者差的平方作为损失函数:
L ( w ) = 1 2 [ Q ( “北京”,“上海”; w ) − y ^ ] 2 . \begin{array}{rcl}L(\boldsymbol{w})&=&\frac{1}{2}\Big[Q(\text{“北京”,“上海”; }\boldsymbol{w})-\widehat{y}\Big]^2.\end{array} L(w)=21[Q(“北京”,“上海”; w)−y ]2.
此处把 y ^ \widehat{y} y 看做常数,尽管它依赖于 w w w。计算损失函数的梯度:
∇ w L ( w ) = ( q ^ − y ^ ) ⏟ 记作 δ ⋅ ∇ w Q ( “北京”,“上海”; w ) , \begin{array}{rcl}\nabla_{w}L(\boldsymbol{w})&=&\underbrace{(\widehat{q}-\widehat{y})}_{\text{记作 }\delta}\cdot\nabla_{\boldsymbol{w}}Q(\text{“北京”,“上海”; }\boldsymbol{w}),\\\end{array} ∇wL(w)=记作 δ (q −y )⋅∇wQ(“北京”,“上海”; w),
此处的 δ = q ^ − y ^ = 14 − 15.5 = − 1.5 \delta=\widehat{q}-\widehat{y}=14-15.5=-1.5 δ=q −y =14−15.5=−1.5 称作 TD 误差 (TD error)。做一次梯度下降更新模型参数 w : w: w:
w ← w − α ⋅ δ ⋅ ∇ w Q ( “北京”,“上海” ; w ) . \boldsymbol{w}\:\leftarrow\:\boldsymbol{w}\:-\:\boldsymbol{\alpha}\:\cdot\:\boldsymbol{\delta}\:\cdot\:\nabla_{\boldsymbol{w}}\:Q(\text{“北京”,“上海”};\boldsymbol{w}). w←w−α⋅δ⋅∇wQ(“北京”,“上海”;w).
如果你仍然不理解 TD 算法,那么请换个角度来思考问题。模型估计从北京到上海全程需要 q ^ = 14 \widehat{q}=14 q =14 小时,模型还估计从济南到上海需要 q ⃗ ′ = 11 \vec{q}^{\prime}=11 q′=11 小时。这就相当于模型做了这样的估计:从北京到济南需要的时间为
q ^ − q ^ ′ = 14 − 11 = 3. \widehat q-\widehat q^{\prime}\:=\:14-11\:=\:3. q −q ′=14−11=3.
而我真实花费 r = 4.5 r=4.5 r=4.5 小时从北京到济南。模型的估计与我的真实观测之差为
δ = 3 − 4.5 = − 1.5. \delta\:=\:3-4.5\:=\:-1.5. δ=3−4.5=−1.5.
这就是 TD 误差!以上分析说明 TD 误差 δ \delta δ 就是模型估计与真实观测之差。TD 算法的目的是通过更新参数 w w w 使得损失 L ( w ) = 1 2 δ 2 L(w)=\frac12\delta^2 L(w)=21δ2 减小。
ChatGPT:
TD误差衡量了当前时刻估算的值函数与下一时刻的估算值函数的差异,即当前估算值和通过时间差分学习所得到的预期未来值之间的差距。这个差距被用来更新值函数的参数,以使估算更为准确。
用TD训练DQN
TD算法是一种在线学习算法,可以逐步更新值函数,而不需要等到回合结束。
视频中用到的例子是从纽约到亚特兰大,途径华盛顿,但是道理都是一样的。

如何把TD算法用到DQN?和驾车的例子很像,等式左边是t时刻的Q的估计,等式右边是一个实际观测值加一项关于t+1时刻的Q估计。

等式 U t = R t + γ ⋅ U t + 1 U_t\:=\:R_t+\gamma\cdot U_{t+1}\: Ut=Rt+γ⋅Ut+1
这个等式反映了相邻两个折扣回报之间的关系:t时刻的折扣回报 U t U_t Ut等于t时刻的奖励 R t R_t Rt 加上折扣因子 γ \gamma γ乘以t+1时刻的折扣回报 U t + 1 U_{t+1} Ut+1。
得来的过程如下:

Q ( s t , a t ; w ) ≈ E [ R t + γ ⋅ Q ( S t + 1 , A t + 1 ; w ) ] . Q(s_t,{a_t};\mathbf{w})\approx\mathbb{E}[\mathbb{R}_t+{\gamma}\cdot Q(\mathbb{S}_{t+1},{A_{t+1}};\mathbf{w})]. Q(st,at;w)≈E[Rt+γ⋅Q(St+1,At+1;w)].这个公式两边是两个估计(estimate)

左边是prediction,右边是TD target。

使用TD算法训练DQN的过程如下图:下图中的t+1时刻的Q为什么可以写成max的形式?是因为t+1时刻的action a t + 1 a_{t+1} at+1就是选择t时刻使得Q最大的那个action。

下面是王树森书中具体的推导过程:
下面我们推导训练 DQN 的 TD 算法(严格地讲,此处推导的是“Q 学习算法”,它属于 TD 算法的一种。本节就称其为 TD 算法)。回忆一下回报的定义 : U t = ∑ k = t n γ k − t ⋅ R k :U_t=\sum_{k=t}^n\gamma^{k-t}\cdot R_k :Ut=∑k=tnγk−t⋅Rk, U t + 1 = ∑ k = t + 1 n γ k − t − 1 ⋅ R k U_{t+1}=\sum_{k=t+1}^{n}\gamma^{k-t-1}\cdot R_{k} Ut+1=∑k=t+1nγk−t−1⋅Rk。由 U ι U_{\iota} Uι 和 U t + 1 U_{t+1} Ut+1 的定义可得:
U t = R t + γ ⋅ ∑ k = t + 1 n γ k − t − 1 ⋅ R k ⏟ = U t + 1 . ( 4.1 ) U_t\:=\:R_t+\gamma\cdot\underbrace{\sum_{k=t+1}^n\gamma^{k-t-1}\cdot R_k}_{=U_{t+1}}\:.\quad{(4.1)} Ut=Rt+γ⋅=Ut+1 k=t+1∑nγk−t−1⋅Rk.(4.1)
回忆一下,最优动作价值函数可以写成
Q ⋆ ( s t , a t ) = max π E [ U t ∣ S t = s t , A t = a t ] . ( 4.2 ) Q_{\star}\big(s_{t},a_{t}\big)\:=\:\operatorname*{max}_{\pi}\:\mathbb{E}\Big[U_{t}\big|\:S_{t}=s_{t},A_{t}=a_{t}\Big]. \quad{(4.2)} Q⋆(st,at)=πmaxE[Ut St=st,At=at].(4.2)
从公式 (4.1)和 (4.2)出发,经过一系列数学推导 , 可以得到下面的定理。这个定理是最优贝尔曼方程 (optimal Bellman equations) 的一种形式。
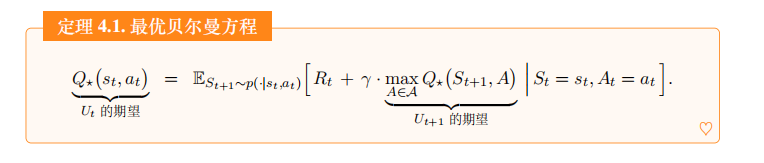
最优贝尔曼方程具体公式如下:
Q ⋆ ( s t , a t ) ⏟ U t 的期望 = E S t + 1 ∼ p ( ⋅ ∣ s t , a t ) [ R t + γ ⋅ max A ∈ A Q ⋆ ( S t + 1 , A ) ⏟ U t + 1 的期望 ∣ S t = s t , A t = a t ] . \underbrace{Q_{\star}(s_{t},a_{t})}_{U_{t}\text{的期望}} = \mathbb{E}_{S_{t+1}\sim p(\cdot|s_{t},a_{t})}\Big[R_{t}+\gamma\cdot\underbrace{\max_{A\in\mathcal{A}}Q_{\star}\big(S_{t+1},A\big)}_{U_{t+1}\text{的期望}} \big | S _ { t }=s_{t},A_{t}=a_{t}\Big]. Ut的期望 Q⋆(st,at)=ESt+1∼p(⋅∣st,at)[Rt+γ⋅Ut+1的期望 A∈AmaxQ⋆(St+1,A) St=st,At=at].
贝尔曼方程的右边是个期望,我们可以对期望做蒙特卡洛近似。当智能体执行动作 a t a_t at 之后,环境通过状态转移函数 p ( s t + 1 ∣ s t , a t ) p(s_{t+1}|s_t,a_t) p(st+1∣st,at) 计算出新状态 s t + 1 s_{t+1} st+1。奖励 R t R_t Rt 最多只依赖于 S t S_t St、 A t A_t At、 S t + 1 S_{t+1} St+1。那么当我们观测到 s t s_t st、 a t a_t at、 s t + 1 s_{t+1} st+1 时,则奖励 R t R_t Rt 也被观测到,记作 r t r_t rt。有了四元组
( s t , a t , r t , s t + 1 ) , \begin{pmatrix}s_t,\:a_t,\:r_t,\:s_{t+1}\end{pmatrix}, (st,at,rt,st+1),
我们可以计算出
r t + γ ⋅ max a ∈ A Q ⋆ ( s t + 1 , a ) . r_{t}+\gamma\cdot\max_{a\in\mathcal{A}}Q_{\star}\big(s_{t+1},a\big). rt+γ⋅a∈AmaxQ⋆(st+1,a).
它可以看做是下面这项期望的蒙特卡洛近似:
E S t + 1 ∼ p ( ⋅ ∣ s t , a t ) [ R t + γ ⋅ max A ∈ A Q ⋆ ( S t + 1 , A ) ∣ S t = s t , A t = a t ] . \mathbb{E}_{S_{t+1}\sim p(\cdot|s_{t},a_{t})}\Big[\left.R_{t}\:+\:\gamma\cdot\max_{A\in\mathcal{A}}Q_{\star}(S_{t+1},A)\:\Big|\:S_{t}=s_{t},A_{t}=a_{t}\:\Big].\right. ESt+1∼p(⋅∣st,at)[Rt+γ⋅A∈AmaxQ⋆(St+1,A) St=st,At=at].
由定理 4.1 和上述的蒙特卡洛近似可得:
Q ⋆ ( s t , a t ) ≈ r t + γ ⋅ max a ∈ A Q ⋆ ( s t + 1 , a ) . ( 4.3 ) Q_{\star}\big(s_{t},a_{t}\big)\:\approx\:r_{t}+\gamma\cdot\operatorname*{max}_{a\in\mathcal{A}}Q_{\star}\big(s_{t+1},a\big). \quad{(4.3)} Q⋆(st,at)≈rt+γ⋅a∈AmaxQ⋆(st+1,a).(4.3)
这是不是很像驾驶时间预测问题?左边的 Q ⋆ ( s t , a t ) Q_\star(s_t,a_t) Q⋆(st,at) 就像是模型预测“北京到上海”的总时间, r t r_t rt 像是实际观测的“北京到济南”的时间, γ ⋅ max a ∈ A Q ⋆ ( s t + 1 , a ) \gamma\cdot\max_{a\in\mathcal{A}}Q_\star(s_{t+1},a) γ⋅maxa∈AQ⋆(st+1,a) 相当于模型预测剩余路程“济南到上海”的时间。见图 4.4 中的类比。
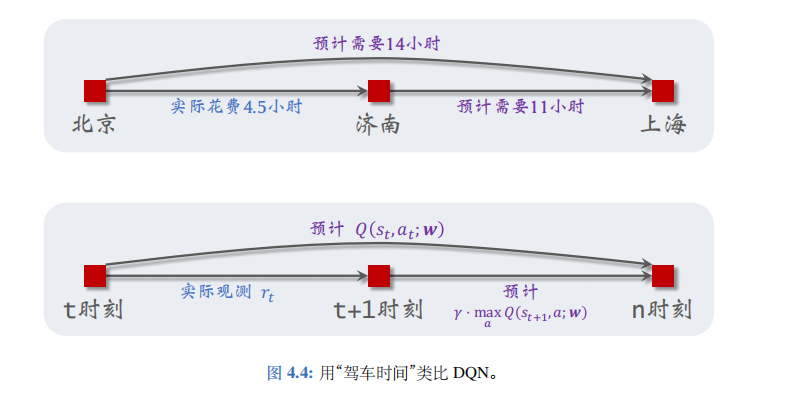
把公式 (4.3) 中的最优动作价值函数 Q ⋆ ( s , a ) Q_\star(s,a) Q⋆(s,a) 替换成神经网络 Q ( s , a ; w ) Q(s,a;\boldsymbol{w}) Q(s,a;w), 得到:
Q ( s t , a t ; w ) ⏟ 预测 q ^ t ≈ r t + γ ⋅ max a ∈ A Q ( s t + 1 , a ; w ) ⏟ TD 目标 y t ^ \underbrace{Q\left(s_t,a_t;\boldsymbol{w}\right)}_{\text{预测 }\widehat{q}_t}\:\approx\:\underbrace{r_t+\gamma\cdot\max_{a\in\mathcal{A}}Q\left(s_{t+1},a;\:\boldsymbol{w}\right)}_{\text{TD 目标 }\widehat{y_t}} 预测 q t Q(st,at;w)≈TD 目标 yt rt+γ⋅a∈AmaxQ(st+1,a;w)
左边的 q ^ t ≜ Q ( s t , a t ; w ) \widehat{q}_t\triangleq Q(s_t,a_t;w) q t≜Q(st,at;w)是神经网络在 t t t 时刻做出的预测,其中没有任何事实成分。右边的 TD 目标 y ^ t \widehat{y}_t y t 是神经网络在 t + 1 t+1 t+1 时刻做出的预测,它部分基于真实观测到的奖励 r t r_t rt。 q ^ t \widehat{q}_t q t 和 y ^ t \widehat{y}_t y t 两者都是对最优动作价值 Q ⋆ ( s t , a t ) Q_\star(s_t,a_t) Q⋆(st,at) 的估计,但是 y ^ t \widehat{y}_t y t 部分基于事实,因此比 q ^ t \widehat{q}_t q t 更可信。应当鼓励 q ^ t ≜ Q ( s t , a t ; w ) \widehat{q}_t\triangleq Q(s_t,a_t;\boldsymbol{w}) q t≜Q(st,at;w)接近 y ^ t \hat{y}_t y^t。定义损失函数:
L ( w ) = 1 2 [ Q ( s t , a t ; w ) − y ^ t ] 2 . L(\boldsymbol{w})\:=\:\frac{1}{2}\Big[Q(s_{t},a_{t};\:\boldsymbol{w})\:-\:\widehat{y}_{t}\Big]^{2}. L(w)=21[Q(st,at;w)−y t]2.
假装 y ^ \widehat{y} y 是常数3(实际上 y ^ t \widehat{y}_t y t 依赖于 w w w, 但是我们假装 y ^ \widehat{y} y 是常数),计算 L L L 关于 w w w 的梯度:
∇ w L ( w ) = ( q ^ t − y ^ t ) ⏟ TD 误差 δ t ⋅ ∇ w Q ( s t , a t ; w ) . \begin{array}{rcl}\nabla_{\boldsymbol{w}}L(\boldsymbol{w})&=&\underbrace{\left(\widehat{q}_{t}-\widehat{y}_{t}\right)}_{\text{TD 误差}\:\delta_{t}}\:\cdot\:\nabla_{\boldsymbol{w}}\:Q\big(s_{t},a_{t};\:\boldsymbol{w}\big).\end{array} ∇wL(w)=TD 误差δt (q t−y t)⋅∇wQ(st,at;w).
做一步梯度下降,可以让 q ^ t \widehat{q}_t q t 更接近 y ^ t : \widehat{y}_t: y t:
w ← w − α ⋅ δ t ⋅ ∇ w Q ( s t , a t ; w ) . \boldsymbol{w}\leftarrow\boldsymbol{w}-\alpha\cdot\delta_{t}\cdot\nabla_{\boldsymbol{w}}Q\big(s_{t},a_{t};\boldsymbol{w}\big). w←w−α⋅δt⋅∇wQ(st,at;w).
这个公式就是训练 DQN 的 TD 算法。
总结一下:最优行动价值函数是未知的,DQN算法就是用神经网络近似这个最优行动价值函数。

TD算法具体流程如下:

书中介绍的训练流程
首先总结上面的结论。给定一个四元组 ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1), 我们可以计算出 DQN 的预测值
q ^ t = Q ( s t , a t ; w ) , \widehat q_{t}\:=\:Q(s_{t},a_{t};\:\boldsymbol w), q t=Q(st,at;w),
以及 TD 目标和 TD 误差:
y ^ t = r t + γ ⋅ max a ∈ A Q ( s t + 1 , a ; w ) 和 δ t = q ^ t − y ^ t . \widehat{y}_{t}\:=\:r_{t}+\gamma\cdot\operatorname*{max}_{a\in\mathcal{A}}Q\big(s_{t+1},a;\:\boldsymbol{w}\big)\quad\text{和}\quad\delta_{t}\:=\:\widehat{q}_{t}-\widehat{y}_{t}. y t=rt+γ⋅a∈AmaxQ(st+1,a;w)和δt=q t−y t.
TD 算法用这个公式更新 DQN 的参数:
w ← w − α ⋅ δ t ⋅ ∇ w Q ( s t , a t ; w ) . \boldsymbol{w}\:\leftarrow\:\boldsymbol{w}-\alpha\cdot\delta_{t}\cdot\nabla_{\boldsymbol{w}}\:Q\big(s_{t},a_{t};\:\boldsymbol{w}\big). w←w−α⋅δt⋅∇wQ(st,at;w).
注意,算法所需数据为四元组 ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1), 与控制智能体运动的策略 π 无关。这就意味着可以用任何策略控制智能体与环境交互,同时记录下算法运动轨迹,作为训练数据。因此,DQN 的训练可以分割成两个独立的部分:收集训练数据、更新参数 w w w 。
收集训练数据:
我们可以用任何策略函数 π \pi π 去控制智能体与环境交互,这个 π 就叫做行为策略 (behavior policy)。比较常用的是 ϵ \epsilon ϵ-greedy 策略:
a t = { argmax a Q ( s t , a ; w ) , 以概率 ( 1 − ϵ ) ; 均匀抽取 A 中的一个动作 , 以概率 ϵ . \left.a_t\:=\:\left\{\begin{array}{ll}\operatorname{argmax}_aQ(s_t,a;\boldsymbol{w}),&\text{以概率 }(1-\epsilon);\\\text{均匀抽取 }\mathcal{A}\text{ 中的一个动作},&\text{以概率 }\epsilon.\end{array}\right.\right. at={argmaxaQ(st,a;w),均匀抽取 A 中的一个动作,以概率 (1−ϵ);以概率 ϵ.
把智能体在一局游戏中的轨迹记作:
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , ⋯ , s n , a n , r n . s_{1},a_{1},r_{1},\:s_{2},a_{2},r_{2},\:\cdots,\:s_{n},a_{n},r_{n}. s1,a1,r1,s2,a2,r2,⋯,sn,an,rn.
把一条轨迹划分成 n n n 个 ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1) 这种四元组,存入数组,这个数组叫做经验回放数组 (replay buffer) 。
更新 DQN 参数 w : w: w:
随机从经验回放数组中取出一个四元组,记作 ( s j , a j , r j , s j + 1 ) (s_j,a_j,r_j,s_{j+1}) (sj,aj,rj,sj+1)。
设 DQN 当前的参数为 w n o w w_\mathrm{now} wnow, 执行下面的步骤对参数做一次更新,得到新的参数 w n e w w_\mathrm{new} wnew。
1.对 DQN 做正向传播,得到 Q 值:
q ^ j = Q ( s j , a j ; w n o w ) 和 q ^ j + 1 = max a ∈ A Q ( s j + 1 , a ; w n o w ) . \widehat q_{j}\:=\:Q\big(s_{j},a_{j};\:w_{\mathrm{now}}\big)\quad\text{和}\quad\widehat q_{j+1}\:=\:\max_{a\in\mathcal{A}}Q\big(s_{j+1},a;\:w_{\mathrm{now}}\big). q j=Q(sj,aj;wnow)和q j+1=a∈AmaxQ(sj+1,a;wnow).
2.计算 TD 目标和 TD 误差:
y ^ j = r j + γ ⋅ q ^ j + 1 和 δ j = q ^ j − y ^ j . \widehat y_{j}\:=\:r_{j}+\gamma\cdot\widehat q_{j+1}\quad\text{和}\quad\delta_{j}\:=\:\widehat q_{j}-\widehat y_{j}. y j=rj+γ⋅q j+1和δj=q j−y j.
3.对 DQN 做反向传播,得到梯度:
g j = ∇ w Q ( s j , a j ; w n o w ) . g_{j}\:=\:\nabla_{\boldsymbol{w}}\:Q(s_{j},a_{j};\:\boldsymbol{w_{\mathrm{now}}})\:. gj=∇wQ(sj,aj;wnow).
4.做梯度下降更新 DQN 的参数:
w n e w ← w n o w − α ⋅ δ j ⋅ g j . w_\mathrm{new}\:\leftarrow\:w_\mathrm{now}-\alpha\cdot\delta_j\cdot\boldsymbol{g}_j. wnew←wnow−α⋅δj⋅gj.
智能体收集数据、更新 DQN 参数这两者可以同时进行。可以在智能体每执行一个动作之后,对 w w w做几次更新。也可以在每完成一局游戏之后,对 w w w 做几次更新。
注意
上面介绍用 TD 算法训练 DQN, 更准确地说,我们用的 TD 算法叫做 Q 学习算法 (Q-learning)。TD 算法是一大类算法,常见的有 Q 学习和 SARSA。Q 学习的目的是学到最优动作价值函数 Q ⋆ Q_{\star} Q⋆,而 SARSA 的目的是学习动作价值函数 Q π Q_\pi Qπ。后面会介绍 SARSA 算法。
后记
截至2024年1月26日20点28分,学习完深度强化学习的第二个视频,并且结合原书做了详细的笔记。不知道放假回家之前能学习到哪里。
相关文章:

深度强化学习(王树森)笔记02
深度强化学习(DRL) 本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。 参考链接 Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL 源代码链接:https://github.c…...

【分布式技术专题】「分布式技术架构」 探索Tomcat技术架构设计模式的奥秘(Server和Service组件原理分析)
探索Tomcat技术架构设计模式的奥秘 Tomcat系统架构分析Tomcat 整体结构Tomcat总体结构图以 Service 作为“婚姻”1) Service 接口方法列表 2) StandardService 的类结构图方法列表 3) StandardService. SetContainer4) StandardService. addConnector 以 Server 为“居”1) Ser…...

常用的gpt-4 prompt words收集8
本文介绍我最近收集的一些好用的chatgpt-4的prompts,如果你也有好用的提示词可以互相交流一下。 1. I ran into some trouble on my way to work. 迟到原因 2. In my heart, the most delicious coffee is the Hawaii Dirty from Manner. Only the Nong series a…...

【GitHub项目推荐--开源2D 游戏引擎】【转载】
microStudio 是一个可在浏览器中运行的游戏引擎,它拥有一套精美、设计精良、全面的工具,可以非常轻松地帮助你创建 2D 游戏。 你可以在浏览器中访问 microStudio.dev 开始搭建你的游戏,当然你可以克隆现有项目或创建新游戏并开始编码&#x…...

鸿蒙APP的应用场景
鸿蒙APP可以用于多种场合和设备类型,这是鸿蒙系统的分布式能力和多终端适配的优势。以下是一些鸿蒙APP的应用场景,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1.智能手机和平板电脑&am…...
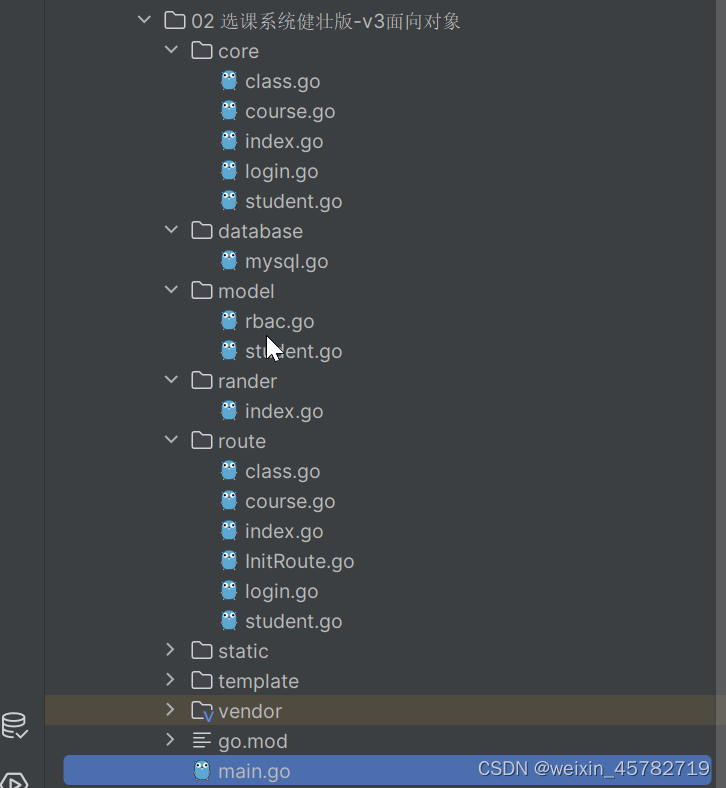
goland课程管理(6)
项目目录结构如下图所示: core包下面: class.go package coreimport "github.com/gin-gonic/gin"func Class1(ctx *gin.Context) {}course.go package coreimport (. "cookie/database". "cookie/model""fmt"…...
)
04.Elasticsearch应用(四)
Elasticsearch应用(四) 1.什么是索引 索引是文档的容器,是一类文档的结合索引是一个逻辑命名空间,它映射到一个或多个主分片,并且可以具有零个或多个副本分片索引中数据分散在Shard上索引的Mapping定义文档字段的类型…...
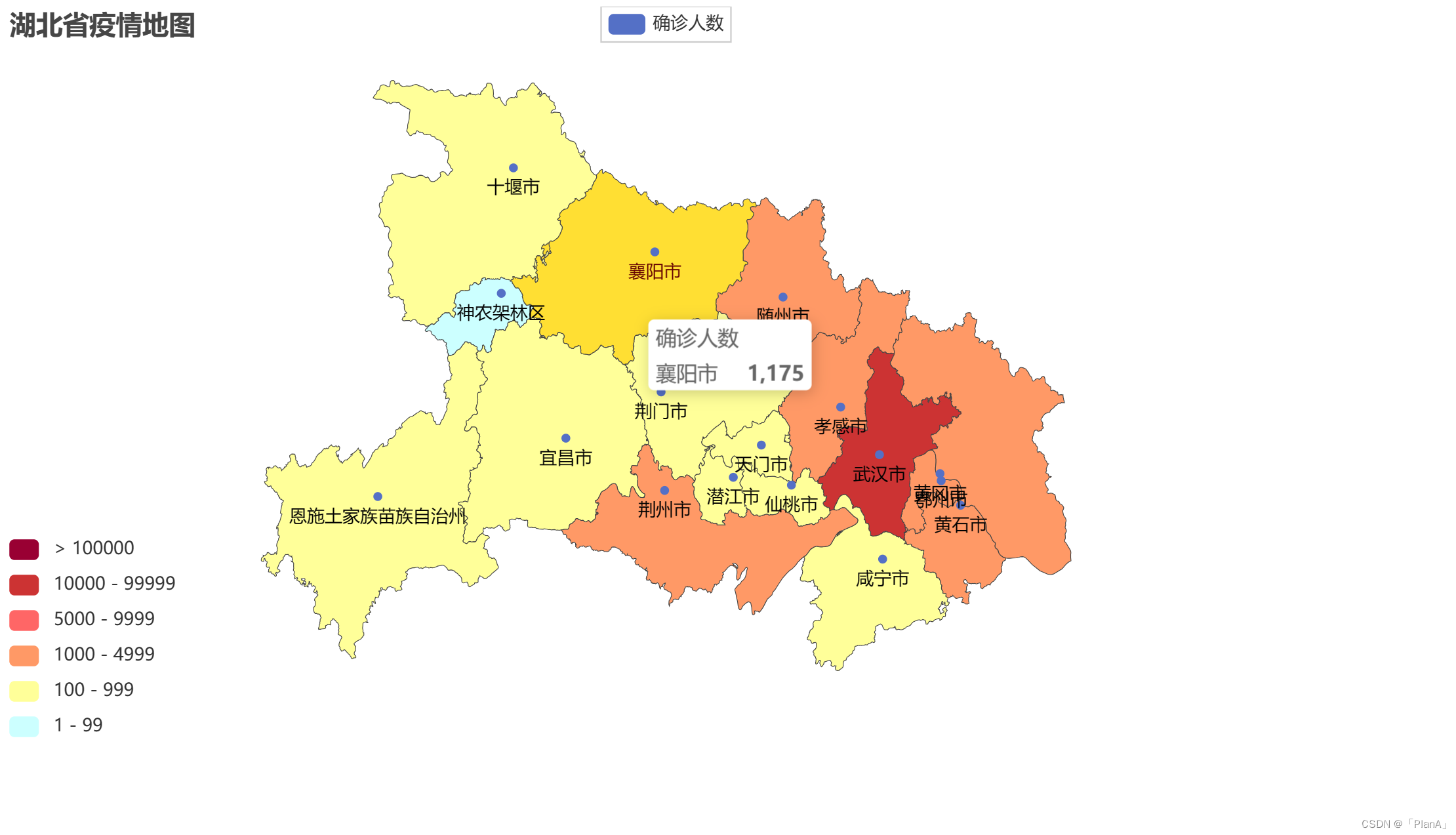
Python之数据可视化(地图)
目录 一 基础地图应用 二 全国疫情图 一 数据准备 二 数据处理 二 湖北省疫情图 一 数据准备 二 数据处理 一 基础地图应用 导入map地图对象 from pyecharts.charts import Map map Map() 写入数据 data [("北京市",100),("上海市"…...
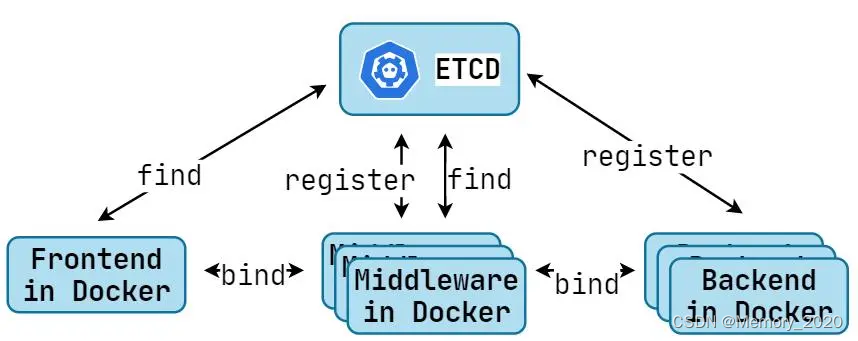
etcd技术解析:构建高可用分布式系统的利器
1. 引言 随着云原生技术的兴起,分布式系统的构建变得愈发重要。etcd作为一个高可用的分布式键值存储系统,在这个领域发挥着至关重要的作用。本文将深入探讨etcd的技术细节,以及如何利用它构建高可用的分布式系统。 2. etcd简介 etcd是一个开…...

Pillow图像处理:从零开始的奇妙之旅
图像处理,就像是一场神奇的冒险,让我们的照片变得更有趣、更生动。而在这个冒险的旅途中,Pillow就如同一位魔法师,为我们开启了无尽的可能性。无论你是刚刚踏入图像处理领域的小白,还是已经略有基础的程序员࿰…...
缓存)
设计一个LRU(最近最少使用)缓存
约束和假设 我们正在缓存什么? 我们正在缓存Web Query的结果我们可以假设输入是有效的,还是需要对其验证? 假设输入是有效的我们可以假设它适应内存吗? 对 编码实现 class Node(object):def __init__(self, results):self.res…...

shell 循环语句
一、命令补充 1. echo 命令 echo -n 表示不换行输出 echo -e 表示输出转义符 常用的转义符有: 选项作用\r光标移至行首,并且不换行\s当前shell的名称,如bash\t插入Tab键,制表符\n输出换行\f换行,但光标仍停留在…...
 命名空间)
C++(1) 命名空间
文章目录 C1. C 概述2.C 相对于 C 语言的增强2.1C 第一行代码2.2 C 补充 bool 类型2.3 作用域运算符2.4 命名空间 namespace2.4.1 命名空间基本内容和开放性2.4.2 多个命名空间操作2.4.3 命名空间函数定义和实现分离2.4.4 匿名命名空间2.4.5 命名空间别名 C 1. C 概述 C 之父…...

【机组】单元模块实验的综合调试与驻机键盘和液晶显示器的使用方式
🌈个人主页:Sarapines Programmer🔥 系列专栏:《机组 | 模块单元实验》⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。 目录 1. 综合实验的调试 1.1 实验…...

React中实现虚拟加载滚动
前言:当一个页面中需要接受接口返回的全部数据进行页面渲染时间,如果数据量比较庞大,前端在渲染dom的过程中需要花费时间,造成页面经常出现卡顿现象。 需求:通过虚拟加载,优化页面渲染速度 缺点:…...

vue中的Mutations
目录 一:介绍 二:例子 一:介绍 Vuex 中的 mutation 非常类似于事件: 每个 mutation 都有一个字符串的 事件类型 (type) 和 一个 回调函数 (handler)。这个回调函数就是我们实际进行状态更改的函数,并且它会接受 sta…...
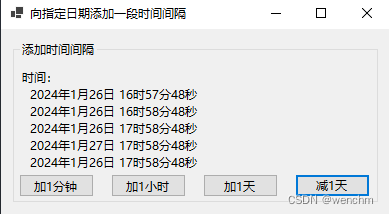
C#用 DateAndTime.DateAdd方法和DateTime.Add(TimeSpan) 方法分别添加一段时间间隔
目录 一、基本方法 1.用 DateAndTime.DateAdd方法添加一段时间间隔 2.用DateTime.Add方法添加一段时间间隔 二、实例 1.实例1:用 DateAndTime.DateAdd方法 2.实例2:用DateTime.Add方法 一、基本方法 1.用 DateAndTime.DateAdd方法添加一段时间间隔…...
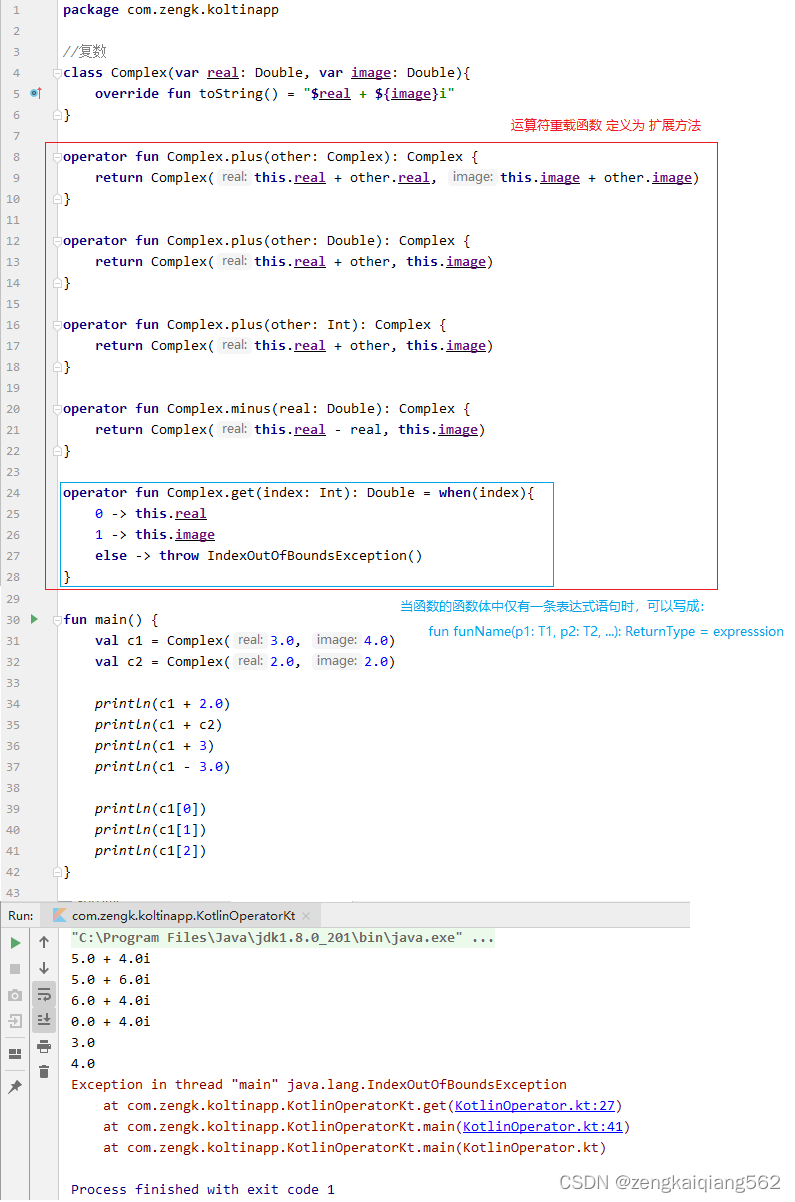
四、Kotlin 表达式
1. 常量 & 变量 1.1 可读写变量(var) var x initValue // x 称为可读写变量注意:当 var 声明的变量做成员属性时,默认提供 setter/getter 方法。 1.2 只读变量(val) val x initValue // x 称为只…...
Web开发4:单元测试
在Web开发中,单元测试是一种重要的开发实践,它可以帮助我们确保代码的质量和可靠性。通过编写和运行单元测试,我们可以验证代码的正确性,减少错误和缺陷,并提高代码的可维护性。本文将介绍单元测试的概念、好处以及如何…...

Ubuntu 16 让ufw防火墙控制docker容器中所有端口
使用docker ps 查询docker在运行端口。 rootai-0003:~# docker ps CONTAINER ID IMAGE COMMAND CREATED STATUS PORTS …...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
