空间中任意一点到球的截面的最短距离
假设球的球心坐标为Oball={x0,y0,z0}O_{ball}=\{x_0,y_0,z_0\}Oball={x0,y0,z0},球的半径为rrr,球的方程为(x−x0)2+(y−y0)2+(z−z0)2=r2(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=r^2(x−x0)2+(y−y0)2+(z−z0)2=r2球的一截面的方程为Ax+By+Cz+1=0Ax+By+Cz+1=0Ax+By+Cz+1=0该截面为一个空间中的圆,球心Oball={x0,y0,z0}O_{ball}=\{x_0,y_0,z_0\}Oball={x0,y0,z0}在截面上的垂足即为空间中圆的圆心。假设圆上的任意三点的坐标分别为J(x1,y1,z1)J(x_1,y_1,z_1)J(x1,y1,z1),K(x2,y2,z2)K(x_2,y_2,z_2)K(x2,y2,z2),L(x3,y3,z3)L(x_3,y_3,z_3)L(x3,y3,z3),圆心坐标为P=(xp,yp,zp)P=(x_p,y_p,z_p)P=(xp,yp,zp),则球心Oball={x0,y0,z0}O_{ball}=\{x_0,y_0,z_0\}Oball={x0,y0,z0}在截面上的投影为PPP,可以得到下列向量OballP→=(xp−x0,yp−y0,zp−z0)JK→=(x2−x1,y2−y1,z2−z1)JL→=(x3−x1,y3−y1,z3−z1)\overrightarrow{O_{ball}P}=(x_p-x_0,y_p-y_0,z_p-z_0)\\\overrightarrow{JK}=(x_2-x_1,y_2-y_1,z_2-z_1)\\\overrightarrow{JL}=(x_3-x_1,y_3-y_1,z_3-z_1)OballP=(xp−x0,yp−y0,zp−z0)JK=(x2−x1,y2−y1,z2−z1)JL=(x3−x1,y3−y1,z3−z1)由向量垂直关系OballP→⊥JK→\overrightarrow{O_{ball}P}\bot\overrightarrow{JK}OballP⊥JK以及OballP→⊥JL→\overrightarrow{O_{ball}P}\bot\overrightarrow{JL}OballP⊥JL可以得到(xp−x0)(x2−x1)+(yp−y0)(y2−y1)+(zp−z0)(z2−z1)=0(xp−x0)(x3−x1)+(yp−y0)(y3−y1)+(zp−z0)(z3−z1)=0(x_p-x_0)(x_2-x_1)+(y_p-y_0)(y_2-y_1)+(z_p-z_0)(z_2-z_1)=0\\(x_p-x_0)(x_3-x_1)+(y_p-y_0)(y_3-y_1)+(z_p-z_0)(z_3-z_1)=0(xp−x0)(x2−x1)+(yp−y0)(y2−y1)+(zp−z0)(z2−z1)=0(xp−x0)(x3−x1)+(yp−y0)(y3−y1)+(zp−z0)(z3−z1)=0由J,K,LJ,K,LJ,K,L三点均在截面上,则有(x1y1z1x2y2z2x3y3z3)(ABC)+(111)=0\begin{pmatrix}x_1&y_1&z_1\\x_2&y_2&z_2\\x_3&y_3&z_3\end{pmatrix}\begin{pmatrix}A\\B\\C\end{pmatrix}+\begin{pmatrix}1\\1\\1\end{pmatrix}=0x1x2x3y1y2y3z1z2z3ABC+111=0解得(ABC)=−(x1y1z1x2y2z2x3y3z3)−1(111)\begin{pmatrix}A\\B\\C\end{pmatrix}=-\begin{pmatrix}x_1&y_1&z_1\\x_2&y_2&z_2\\x_3&y_3&z_3\end{pmatrix}^{-1}\begin{pmatrix}1\\1\\1\end{pmatrix}ABC=−x1x2x3y1y2y3z1z2z3−1111因为点PPP在截面上,所以Axp+Byp+Czp+1=0Ax_p+By_p+Cz_p+1=0Axp+Byp+Czp+1=0,联立方程组得{(xp−x0)(x2−x1)+(yp−y0)(y2−y1)+(zp−z0)(z2−z1)=0(xp−x0)(x3−x1)+(yp−y0)(y3−y1)+(zp−z0)(z3−z1)=0Axp+Byp+Czp+1=0\begin{equation*}\begin{cases} (x_p-x_0)(x_2-x_1)+(y_p-y_0)(y_2-y_1)+(z_p-z_0)(z_2-z_1)=0\\ (x_p-x_0)(x_3-x_1)+(y_p-y_0)(y_3-y_1)+(z_p-z_0)(z_3-z_1)=0 \\ Ax_p+By_p+Cz_p+1=0 \end{cases}\end{equation*}⎩⎨⎧(xp−x0)(x2−x1)+(yp−y0)(y2−y1)+(zp−z0)(z2−z1)=0(xp−x0)(x3−x1)+(yp−y0)(y3−y1)+(zp−z0)(z3−z1)=0Axp+Byp+Czp+1=0解得(xpypzp)=(x2−x1y2−y1z2−z1x3−x1y3−y1z3−z1ABC)−1(x0(x2−x1)+y0(y2−y1)+z0(z2−z1)x0(x3−x1)+y0(y3−y1)+z0(z3−z1)−1)\begin{pmatrix}x_p\\y_p\\z_p\end{pmatrix}=\begin{pmatrix}x_2-x_1&y_2-y_1&z_2-z_1\\x_3-x_1&y_3-y_1&z_3-z_1\\A&B&C\end{pmatrix}^{-1}\begin{pmatrix}x_0(x_2-x_1)+y_0(y_2-y_1)+z_0(z_2-z_1)\\x_0(x_3-x_1)+y_0(y_3-y_1)+z_0(z_3-z_1)\\-1\end{pmatrix}xpypzp=x2−x1x3−x1Ay2−y1y3−y1Bz2−z1z3−z1C−1x0(x2−x1)+y0(y2−y1)+z0(z2−z1)x0(x3−x1)+y0(y3−y1)+z0(z3−z1)−1球心到截面的距离为d1=∣Ax0+By0+Cz0+1∣A2+B2+C2d_1=\frac{|Ax_0+By_0+Cz_0+1|}{\sqrt{A^2+B^2+C^2}}d1=A2+B2+C2∣Ax0+By0+Cz0+1∣空间中圆的半径为rcircle=r2−d12r_{circle}=\sqrt{r^2-d_1^2}rcircle=r2−d12。
假设空间中任意一点m(xm,ym,zm)m(x_m,y_m,z_m)m(xm,ym,zm),该点到截面的距离为d2=∣Axm+Bym+Czm+1∣A2+B2+C2d_2=\frac{|Ax_m+By_m+Cz_m+1|}{\sqrt{A^2+B^2+C^2}}d2=A2+B2+C2∣Axm+Bym+Czm+1∣垂足为Q=(xq,yq,zq)Q=(x_q,y_q,z_q)Q=(xq,yq,zq),则有(xqyqzq)=(x2−x1y2−y1z2−z1x3−x1y3−y1z3−z1ABC)−1(xm(x2−x1)+ym(y2−y1)+zm(z2−z1)xm(x3−x1)+ym(y3−y1)+zm(z3−z1)−1)\begin{pmatrix}x_q\\y_q\\z_q\end{pmatrix}=\begin{pmatrix}x_2-x_1&y_2-y_1&z_2-z_1\\x_3-x_1&y_3-y_1&z_3-z_1\\A&B&C\end{pmatrix}^{-1}\begin{pmatrix}x_m(x_2-x_1)+y_m(y_2-y_1)+z_m(z_2-z_1)\\x_m(x_3-x_1)+y_m(y_3-y_1)+z_m(z_3-z_1)\\-1\end{pmatrix}xqyqzq=x2−x1x3−x1Ay2−y1y3−y1Bz2−z1z3−z1C−1xm(x2−x1)+ym(y2−y1)+zm(z2−z1)xm(x3−x1)+ym(y3−y1)+zm(z3−z1)−1垂足QQQ到圆心PPP的距离为d3=(xp−xq)2+(yp−yq)2+(zp−zq)2d_3=\sqrt{(x_p-x_q)^2+(y_p-y_q)^2+(z_p-z_q)^2}d3=(xp−xq)2+(yp−yq)2+(zp−zq)2则垂足QQQ到空间圆上的最短距离为d4=rcircle−d3d_4=r_{circle}-d_3d4=rcircle−d3,对应的圆上的点的坐标为T=(xt,yt,zt)T=(x_t,y_t,z_t)T=(xt,yt,zt),则该点的坐标满足以下的方程组{(xt−x0)2+(yt−y0)2+(zt−z0)2=r2Axt+Byt+Czt+1=0(xq−xt)2+(yq−yt)2+(zq−zt)2=d42\begin{equation*}\begin{cases} (x_t-x_0)^2+(y_t-y_0)^2+(z_t-z_0)^2=r^2 \\ Ax_t+By_t+Cz_t+1= 0 \\ (x_q-x_t)^2+(y_q-y_t)^2+(z_q-z_t)^2=d_4^2 \end{cases}\end{equation*}⎩⎨⎧(xt−x0)2+(yt−y0)2+(zt−z0)2=r2Axt+Byt+Czt+1=0(xq−xt)2+(yq−yt)2+(zq−zt)2=d42方程1满足点在球面上,方程2满足点在截面上,方程3满足点到垂足QQQ的距离为d4d_4d4。
相关文章:

空间中任意一点到球的截面的最短距离
假设球的球心坐标为Oball{x0,y0,z0}O_{ball}\{x_0,y_0,z_0\}Oball{x0,y0,z0},球的半径为rrr,球的方程为(x−x0)2(y−y0)2(z−z0)2r2(x-x_0)^2(y-y_0)^2(z-z_0)^2r^2(x−x0)2(y−y0)2(z−z0)2r2球的一截面的方程为AxByCz10AxByCz10AxByCz10…...

麦克斯韦方程场分量公式推导
今天看书的时候遇到了一个关于公式推导的问题,阅读该篇前推荐优先阅读—点乘与叉乘是否满足结合律。 已知: E ⃗ t = i k n 2 (...

freertos学习之路6-任务创建和删除
写在最前 由于工作需要,需要开始学习freertos的相关知识,本专题主要记录freertos的相关内容 参考: https://www.bilibili.com/video/BV19g411p7UT 正点原子视频 1. 简介 和一般的OS不同(linux/windows),在…...

科都电气创业板IPO终止:曾计划募资约6亿元,郑春开等学历较低
近日,深圳证券交易所披露的信息显示,科都电气股份有限公司(下称“科都电气”)提交了撤回首次公开发行股票并在创业板上市申请文件的申请,同时保荐机构撤回对该公司的保荐。 因此,深圳证券交易所决定终止对…...

【MySQL】第十六部分 MySQL数据类型详解
【MySQL】第十六部分 MySQL数据类型详解 文章目录【MySQL】第十六部分 MySQL数据类型详解16. MySQL数据类型详解16.1 整数类型16.2 浮点类型16.3 定点数类型16.4 位类型 BIT16.5 日期和时间类型16.6 文本字符串类型16.6.1 CHAR VS VARCHAR类型16.6.2 TEXT类型16.6.3 ENUM类型16…...

Linux手工创建新用户
准备工作(配置流程的理解) Linux中useradd命令即一系列文件操作的结合体,所以我们可以通过查看useradd命令来确认我们手工创建新用户需要完成的文件配置 找到man useradd中涉及的文件部分 对于手工创建用户有用的文件: /etc/pas…...
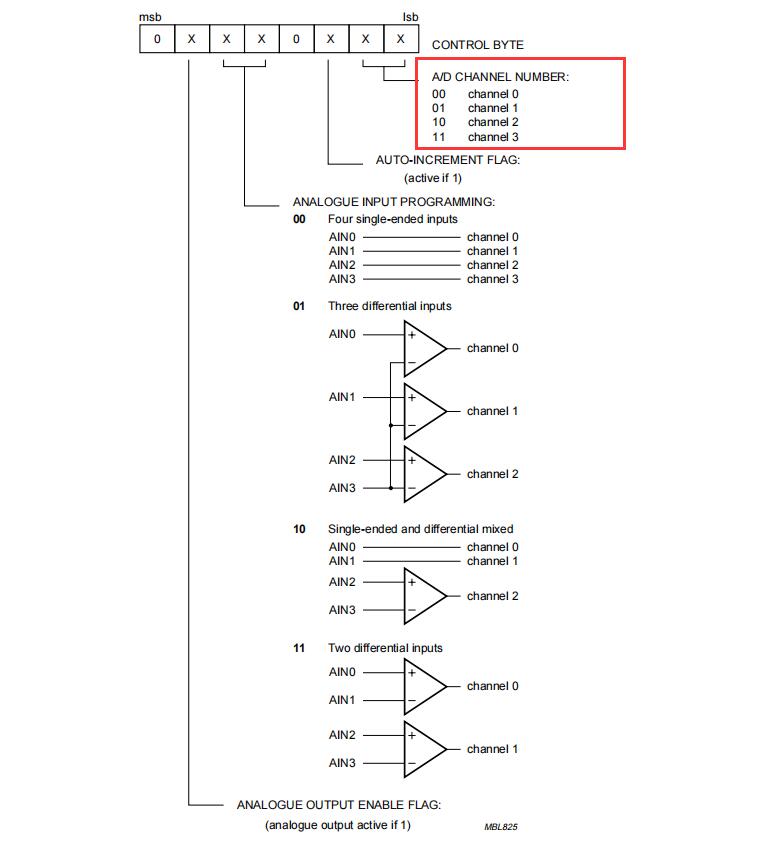
K_A12_003 基于STM32等单片机采集光敏二极管模块参数 串口与OLED0.96双显示
K_A12_003 基于STM32等单片机采集光敏二极管模块参数 串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:四、部分代码说明1、接线引脚定义1.1、STC89C52RC光敏二极管模块1.2、STM32F103C8T6光敏二极管模块五、基础知识…...

天才少年稚晖君
稚晖君 简介主要成就华为天才少年简介 彭志辉,1993年出生于江西吉安,科技圈知名KOL,人称“稚晖君”“野生钢铁侠”,原华为天才少年。 2015年本科毕业于电子科技大学生命科学与技术学院;2018年研究生毕业于电子科技大学信息与通信工程学院;毕业后就职于OPPO研究院AI实验…...
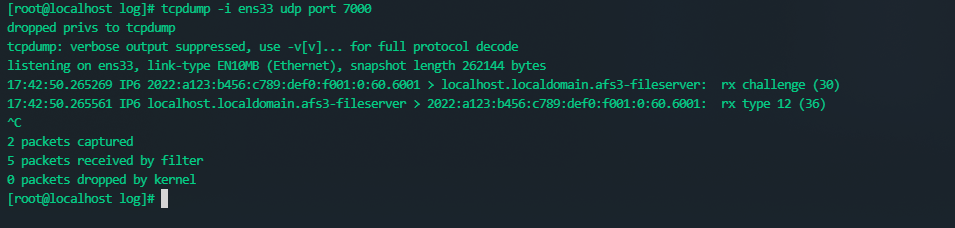
【Linux command 09】tcpdump 命令
tcp一款sniffer工具,是Linux上的抓包工具,嗅探器语法tcpdump (选项)选项-c: 指定要抓取的包数量。注意,是最终要获取这么多个包。例如,指定"-c 10"将获取10个包,但可能已经处理了100个包…...

初始结构体
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 目录 🏡前言 🐰结构体的基础知识 🐰结构体的声明 &#x…...

English Learning - Day56 作业打卡 2023.2.10 周五
English Learning - Day56 作业打卡 2023.2.10 周五引言1. 他把车停错了地方,因此被罚了款。2. 这个事我越想越生气。3.他在这工作的时间比我长。4. 没有奋斗,就不会变强大。5.我一到北京就给你打电话。6. 直到我有了孩子,才意识到我的父母有…...

Python中五个不常见的隐晦用法小结
1. 引言 我已经用Python编程5年了(从2017年开始),直到最近才知道以下几个Python中不常见的用法,确实和人们对直观理解有所出入。 闲话少说,我们直接开始吧! 2. 类中的私有变量不是真正的私有 我们直接上…...

SharkTeam:Move合约开发与合约安全
近期,围绕 Aptos 和 Sui,新兴的高性能 L1链 以及这些新链背后的 Move 智能合约编程语言引起了很多关注,社区也非常活跃,很多开发者和项目已经开始积极转向 Move。但Move相对Solidity差别较大,即使是相对比较接近的Rust…...
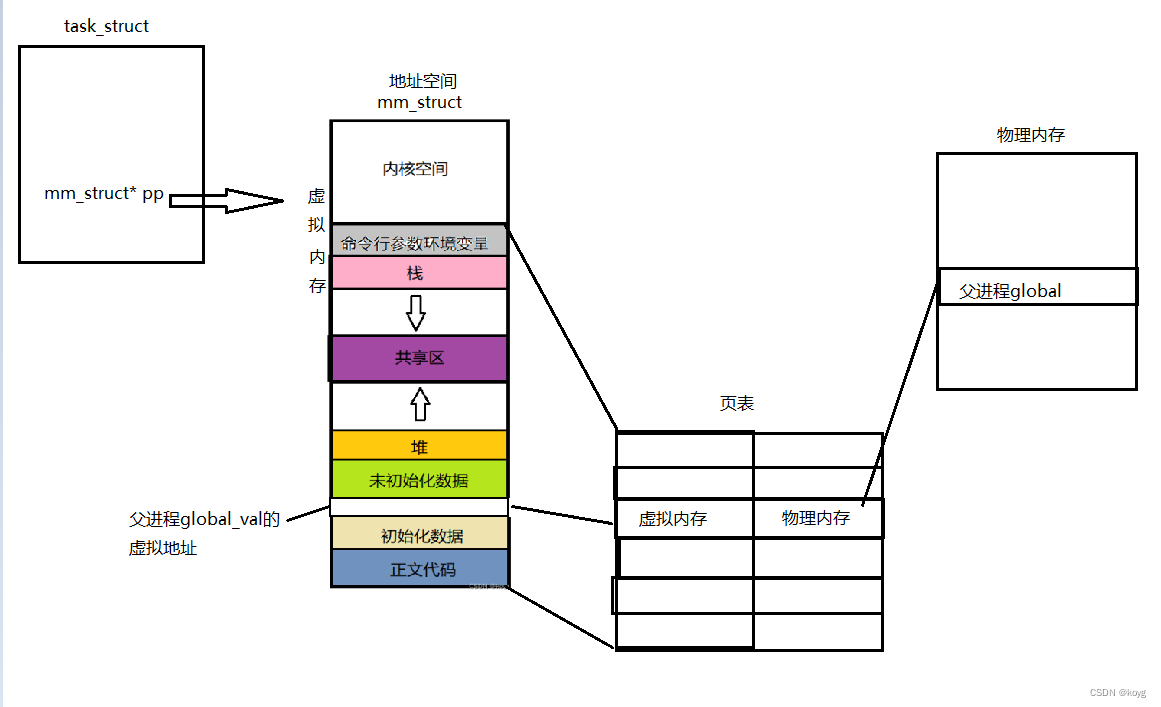
一篇文章学习什么是进程(万字解析,超多知识点)
目录进程概念进程控制块-PCBPCB的内容分类标识符查看进程信息的方法状态fork函数进程状态R运行状态(running)S睡眠状态(sleeping)D磁盘休眠状态(Disk sleep)T停止状态(stopped)X死亡…...
第01章_数据库概述
第01章_数据库概述 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 1. 为什么要使用数据库 持久化(persistence):把数据保存到可掉电式存储设备中以供之后使用。大多数情况下&#x…...

我所理解的高通UEFI之display的流程和移植
UEFI的流程UEFI跟uboot一样在OS加载启动之前,正确的指定启动服务,并向内核传递信息,代替原先的uboot。它包含了上电、驱动实现,以及os环境的建立和应用程序(类似于fastboot)。这个os是UEFI自己独立运行独有…...

iozone -a fsync: I/O error
iozone -a fsync: I/O error iozone: interrupted exit iozone 问题表现是手机老化后重启不开机。检查不开机Log,发现/data/system/packages.xml文件有损坏,pull 离线日志,发现出问题前后的日志也不能pull,pull出来的离线日志解压…...

Element UI框架学习篇(五)
Element UI框架学习篇(五) 1 准备工作 1.1 在zlz包下创建数据传输对象类EmpDTO package com.zlz.dto;import lombok.AllArgsConstructor; import lombok.Data; import lombok.NoArgsConstructor;//根据前台来的 Data public class EmpDTO {private String name;private Stri…...
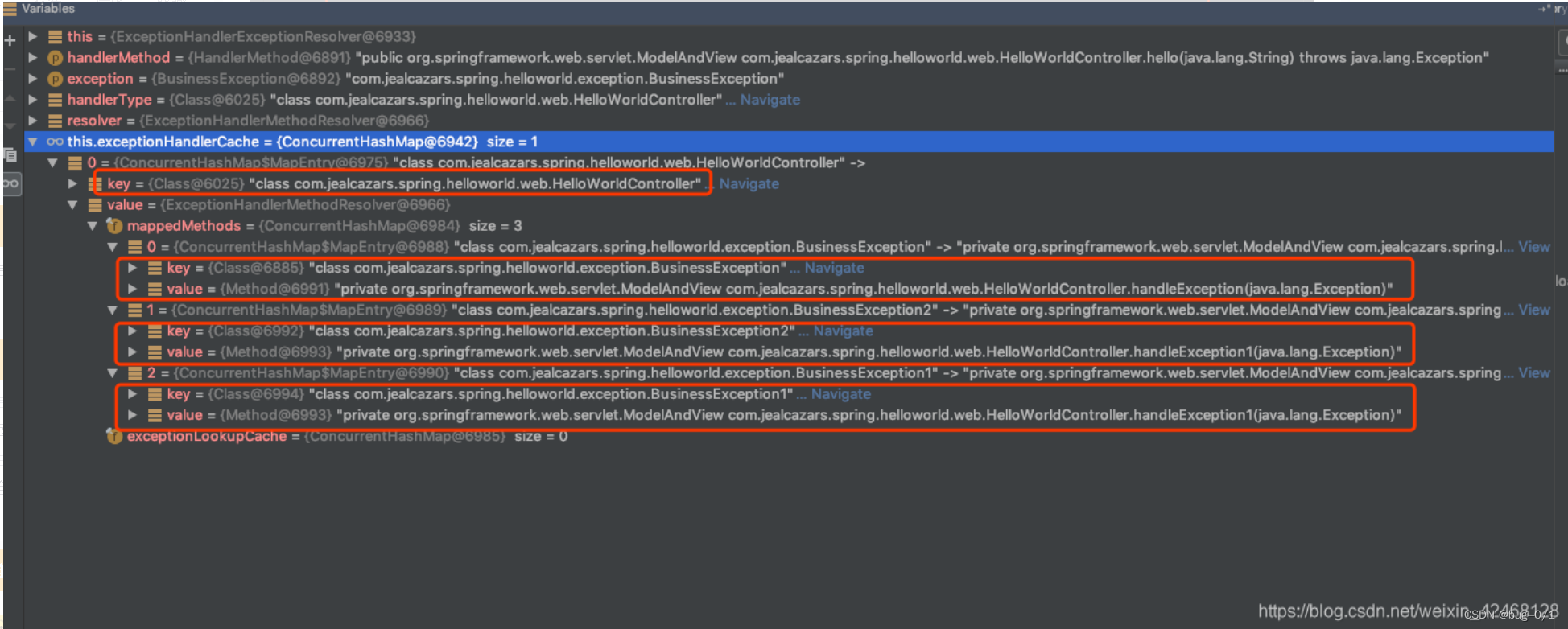
SpringBoot 全局异常处理用法及原理
SpringBoot 全局异常处理用法及原理 Springboot或springMVC项目中, 我们一般会设置一个全局异常处理, 来对异常进行兜底。 业务代码执行过程中抛出的异常, 如果业务逻辑没有主动捕获,那么异常就会一直往上抛,最后进入…...

浏览器中HTTP请求流程是如何处理的
HTTP 是一种允许浏览器向服务器获取资源的协议,是 Web 的基础,通常由浏览器发起请求,用来获取不同类型的文件,例如 HTML 文件、CSS 文件、JavaScript 文件、图片、视频等。 浏览器端发起 HTTP 请求流程: 1. 构建请求…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...

6.9本日总结
一、英语 复习默写list11list18,订正07年第3篇阅读 二、数学 学习线代第一讲,写15讲课后题 三、408 学习计组第二章,写计组习题 四、总结 明天结束线代第一章和计组第二章 五、明日计划 英语:复习l默写sit12list17&#…...
