备战蓝桥杯---动态规划(理论基础)
目录
动态规划的概念:
解决多阶段决策过程最优化的一种方法
阶段:
状态:
决策:
策略:
状态转移方程:
适用的基本条件
1.具有相同的子问题
2.满足最优子结构
3.满足无后效性
动态规划的实现方式:
动态规划的概念:
解决多阶段决策过程最优化的一种方法
阶段:
把问题分成几个相互联系的有顺序的环节。
状态:
某一阶段的出发位置
决策:
从某一状态演变到下一个状态的选择
策略:
从开始到终点的决策序列。
状态转移方程:
从i到i+1状态的演变规律。
适用的基本条件
1.具有相同的子问题
(1)保证这个问题可以分解成几个子问题并且可以用他们来解决这个问题。
(2)这些子问题也可以分解成相同的子问题。
2.满足最优子结构
问题的最优解包含着他的子问题的最优解,即此后决策必须基于上一次产生的最优决策。
举个栗子:
假如A是当前的最优策略,那么,我们要保证下一次的最优解一定是在A的基础上产生的,而不能是由当前的不是最优的策略导出的。
其实,动态规划是一种分阶段贪心的过程,我们要确保最长远的利益来自于每一步当前的最优利益。

就像这一题,我们选一个路径使他们的和%4最小,显然,如果我们只求当前%4的最小值,无法推出来下一步的最优解。
像这样的情况,我们可以重新考虑状态转移方程,我们发现,每一个余数都有存在的价值,于是我们可以把存在的余数记下来,再用他们去求下一个状态。
3.满足无后效性
要包含所有影响答案的因素,即它用于解决当前问题与过去状态无关的问题
举个例子:
大家应该都写过走楼梯的递归问题。a[i]=a[i-1]+a[i-2]。但是,如果有这么一个规定:走过50楼的人不能再走100楼,显然这样子在100楼时,我们不知道前面的99与98是否走过。
于是,我们应该再记录一个值表示是否踏过50,
我们不妨记f[i][0]为没有上过50,f[i][1]为上过50,这样的话,我们在i<50前用f[i][0]=f[i-1][0]+f[i-2][0]; f[i][1]=0;
i==50: f[50][0]=0,f[50][1]=f[49][0]+f[48][0],
i>50&&i<100: f[i][0]=f[i-1][0]+f[i-2][0],f[i][1]=f[i-1][1]+f[i-2][0];
i==100:f[100][0]=f[99][0]+f[98][0],f[100][1]=0;
i>100:f[i][0]=f[i-1][0]+f[i-2][0];f[i][1]=f[i-1][0]+f[i-2][0];
动态规划的实现方式:
1.递推(直接用for循环)
2.记忆化搜索
相关文章:

备战蓝桥杯---动态规划(理论基础)
目录 动态规划的概念: 解决多阶段决策过程最优化的一种方法 阶段: 状态: 决策: 策略: 状态转移方程: 适用的基本条件 1.具有相同的子问题 2.满足最优子结构 3.满足无后效性 动态规划的实现方式…...
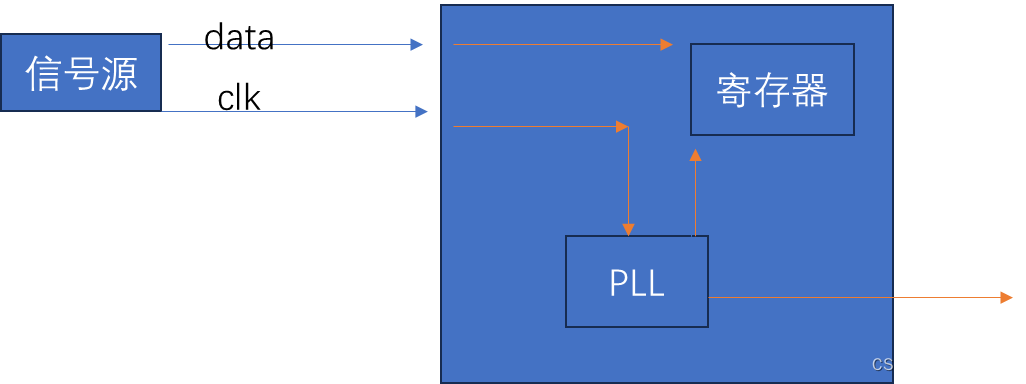
FPGA_ip_pll
常使用插件管理器进行ip核的配置,ip核分为计算,存储,输入输出,视频图像处理,接口,调试等。 一 pll ip核简介 pll 即锁相环,可以对输入到fpga的时钟信号,进行分频,倍频&…...

【实验3】统计某电商网站买家收藏商品数量
文章目录 一、实验目的和要求∶二、实验任务∶三、实验准备方案,包括以下内容:实验内容一、实验环境二、实验内容与步骤(过程及数据记录):三、实验结果分析、思考题解答∶四、感想、体会、建议∶一、实验目的和要求∶ 现有某电商网站用户对商品的收藏数据,记录了用户收藏…...
【Qt】Android上运行keeps stopping, Desktop上正常
文章目录 问题 & 背景背景问题 解决方案One More ThingTake Away 问题 & 背景 背景 在文章【Qt】最详细教程,如何从零配置Qt Android安卓环境中,我们在Qt中配置了安卓开发环境,并且能够正常运行。 但笔者在成功配置并完成上述文章…...
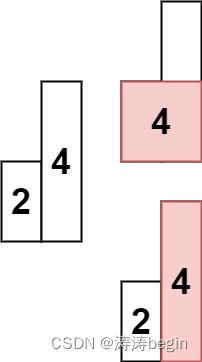
算法学习打卡day47|单调栈系列题目
单调栈题目思路 通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。时间复杂度为O(n)。单调栈的本质是空间换时间,因为在遍历的过程中需要用一个栈来记录右边第一个比当前元…...
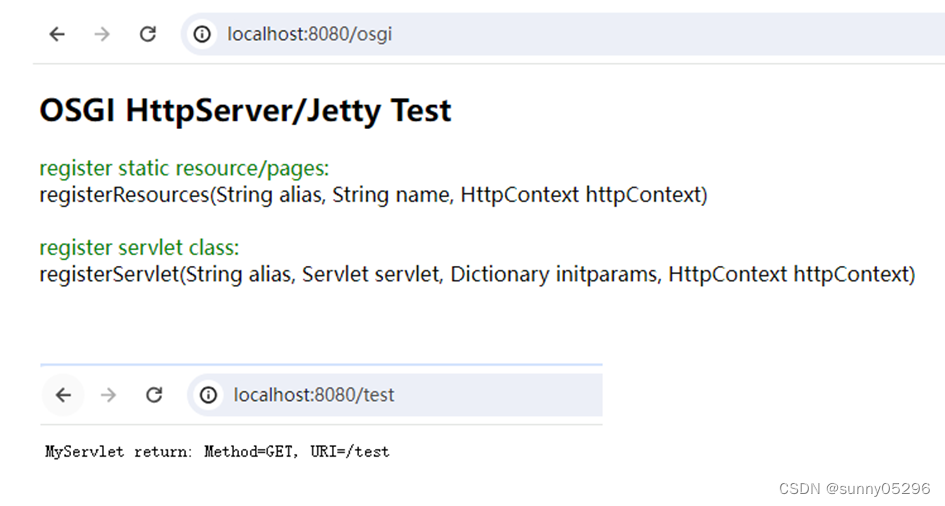
Maven构建OSGI+HttpServer应用
Maven构建OSGIHttpServer应用 官网(https://eclipse.dev/equinox/server/http_in_equinox.php)介绍有两种方式: 一种是基于”org.eclipse.equinox.http”包的轻量级实现,另一种是基于”org.eclipse.equinox.http.jetty”包&#…...

chrome扩展插件常用文件及作用
Chrome扩展通常包含以下常用文件及其作用: manifest.json: 描述了扩展的基本信息,如名称、版本、权限、图标等。定义了扩展的各种组件和功能,包括后台脚本、内容脚本、页面、浏览器动作按钮等。 background.js: 后台脚…...

PdfFactory Pro软件下载以及序列号注册码生成器
PdfFactory Pro注册机是一款针对同名虚拟打印机软件所推出的用户名和序列号生成器。PdfFactory Pro是一款非常专业的PDF虚拟打印软件,通过使用这款注册机,就能帮助用户免费获取注册码,一键激活,永久免费使用。 pdffactory7注册码如…...
jsp康养小镇管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 JSP康养小镇管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&a…...

Android 无操作之后定时退出
android定时器监用户听对页面无操作5分钟退出登录实现 - 简书 private long advertisingTime 600000;///定时结束退出登录10分(分钟)600000毫秒public CountDownTimer countDownTimer;Overrideprotected void onResume() {super.onResume();//启动定时if (isTimedExitApp()) …...
CMS 检测神器:CMSeek 保姆级教程(附链接)
一、介绍 CMSeek(Content Management System Exploitation and Enumeration Toolkit)是一款用于检测和利用网站上可能存在的内容管理系统(CMS)漏洞的开源工具。它旨在帮助安全研究人员和渗透测试人员识别目标网站所使用的CMS&…...
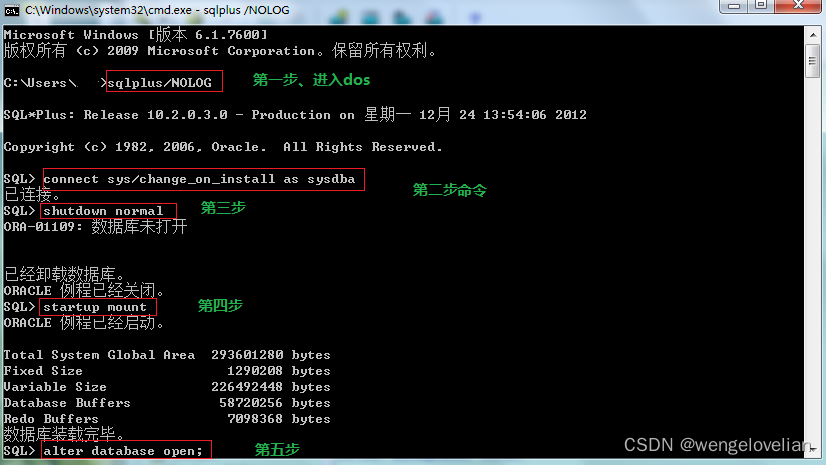
oracle 启动命令以及ORA-01033问题处理、删除归档日志
1 启动数据库:startup 2 关闭数据库:Shutdown immediate 3 查看监听状态:lsnrctl status 4 启动监听:lsnrctl start 5 停止监听:lsnrctl stop 常见问题 1、在服务器重启后会出现,Oracle ORA-01033: ORAC…...
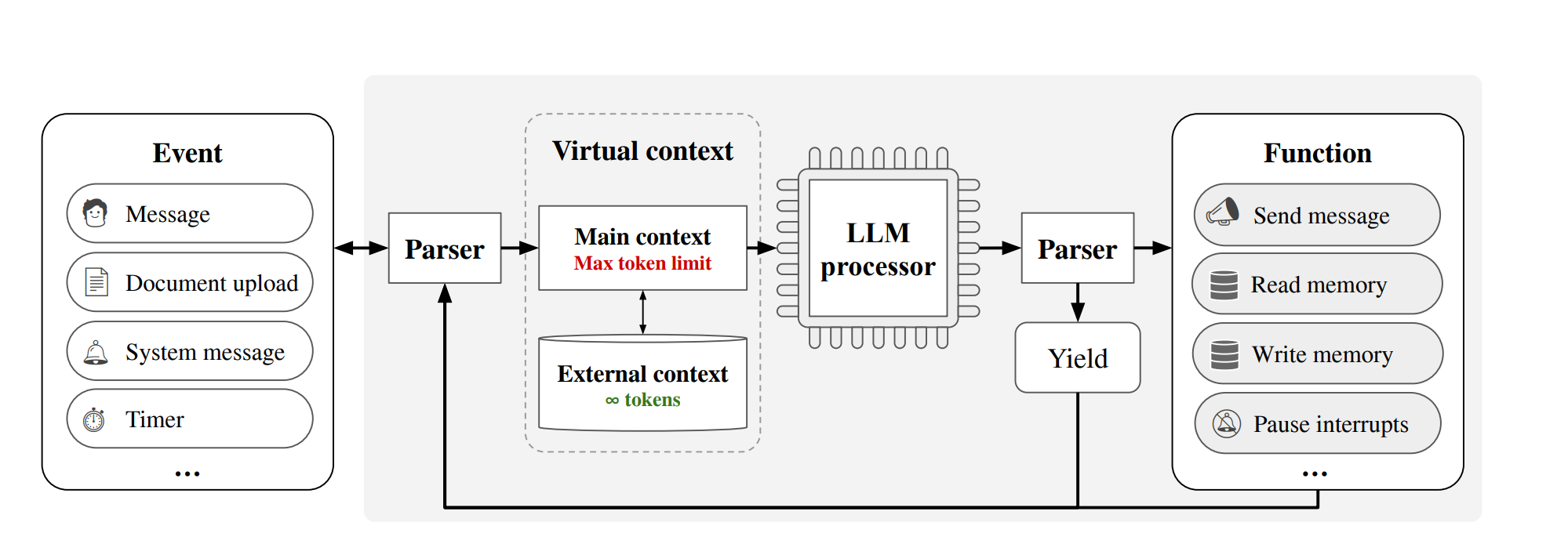
【大模型上下文长度扩展】MedGPT:解决遗忘 + 永久记忆 + 无限上下文
MedGPT:解决遗忘 永久记忆 无限上下文 问题:如何提升语言模型在长对话中的记忆和处理能力?子问题1:有限上下文窗口的限制子问题2:复杂文档处理的挑战子问题3:长期记忆的维护子问题4:即时信息检…...
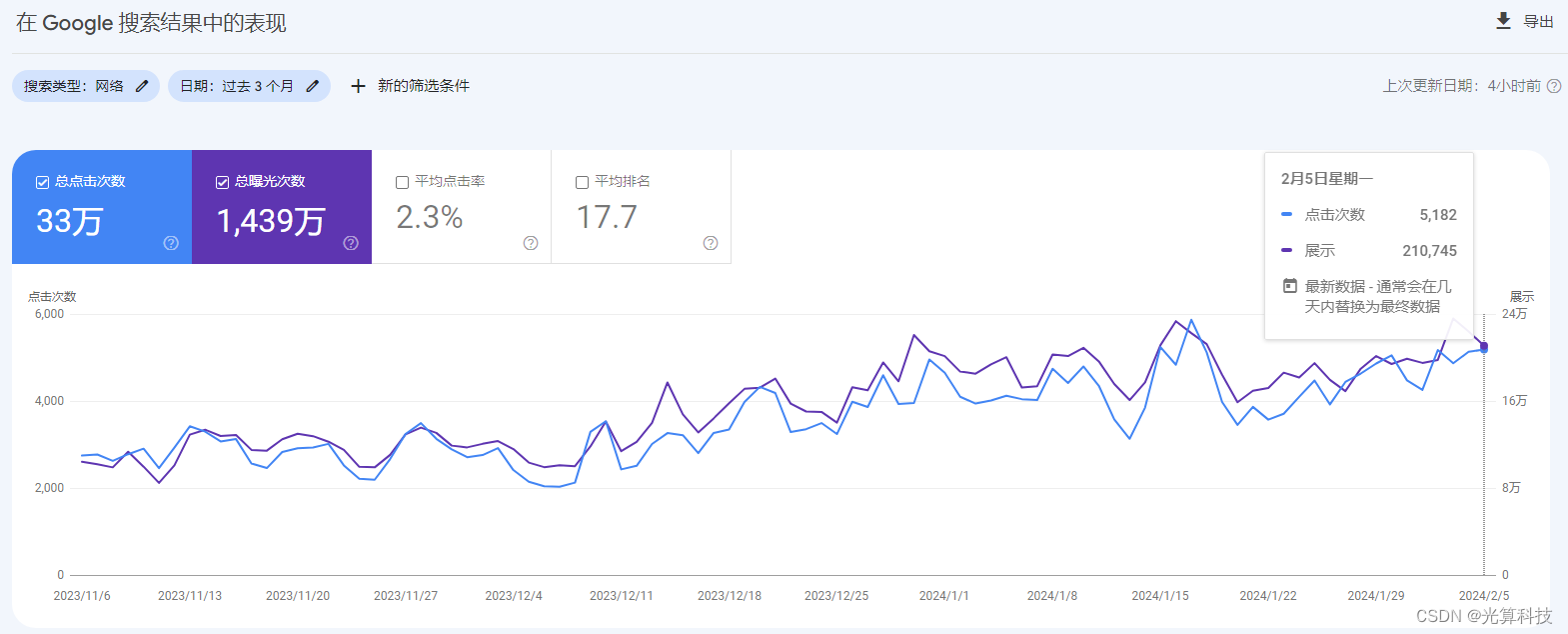
谷歌seo搜索引擎优化有什么思路?
正常做seo哪有那么多思路,其实就那么几种方法,无非就关键词,站内优化,外链,可以说万变不离其宗,但如果交给我们,你就可以实现其他的思路,或者说玩法 收录可以说是一个网站的基础&…...

腾讯云与IBM共同打造“高性能计算服务解决方案“
腾讯云与IBM共同打造"高性能计算服务解决方案" 腾讯云与IBM达成战略合作,对优势产品及服务进行深度集成,基于腾讯云产品及服务,共同打造"腾讯-IBM混合云与人工智能解决方案"。双方通过更为紧密的嵌入式解决方案的深度合…...

【SparkML实践7】特征选择器FeatureSelector
本节介绍了用于处理特征的算法,大致可以分为以下几组: 提取(Extraction):从“原始”数据中提取特征。转换(Transformation):缩放、转换或修改特征。选择(Selection&…...

LeetCode983. Minimum Cost For Tickets——动态规划
文章目录 一、题目二、题解 一、题目 You have planned some train traveling one year in advance. The days of the year in which you will travel are given as an integer array days. Each day is an integer from 1 to 365. Train tickets are sold in three differen…...
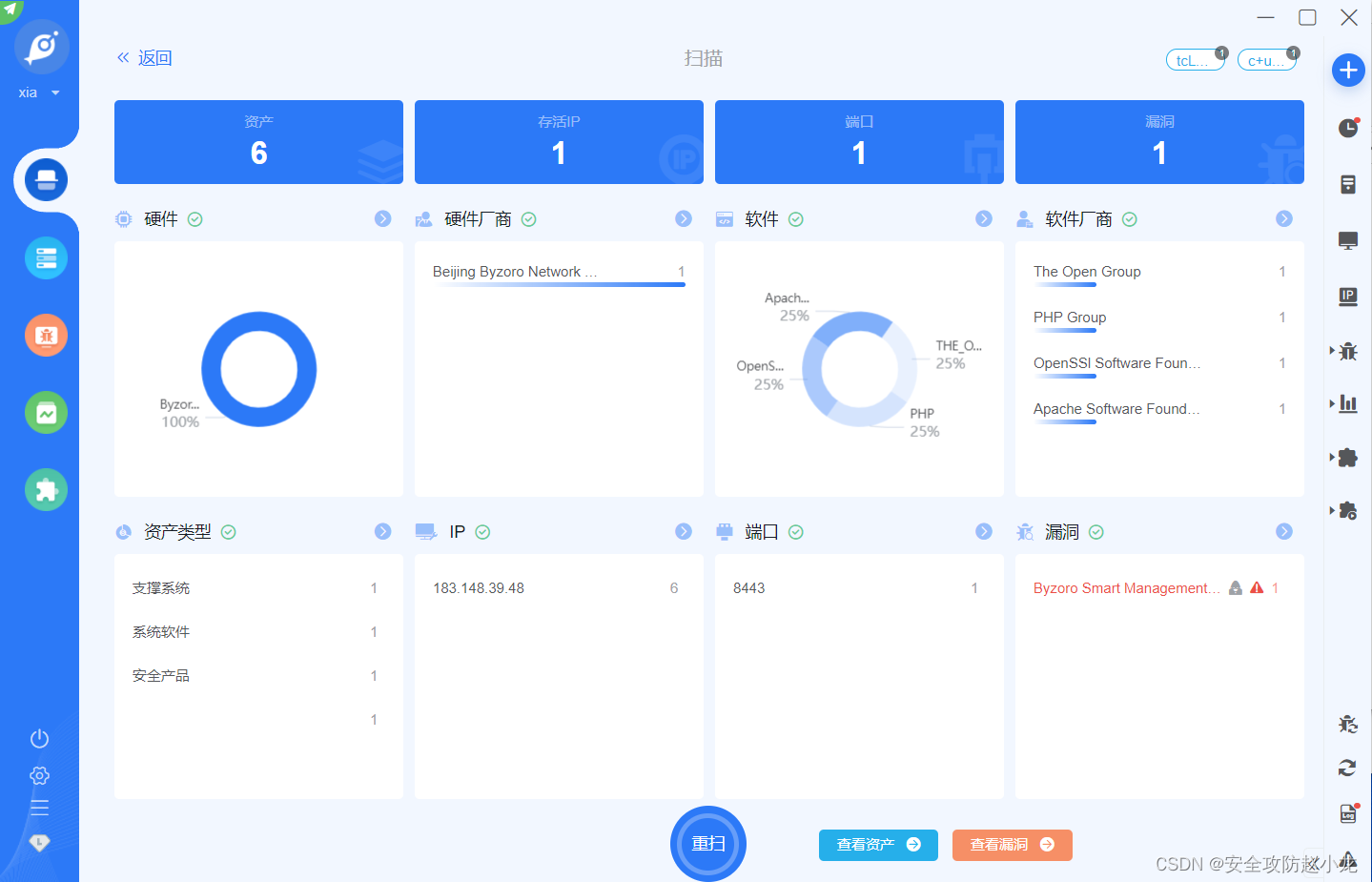
百卓Smart管理平台 uploadfile.php 文件上传漏洞【CVE-2024-0939】
百卓Smart管理平台 uploadfile.php 文件上传漏洞【CVE-2024-0939】 一、 产品简介二、 漏洞概述三、 影响范围四、 复现环境五、 漏洞复现手动复现小龙验证Goby验证 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工…...

项目中常用的一些数据库及缓存
1、常见的开发工具介绍 MySQL: MySQL是一种流行的开源关系型数据库管理系统(RDBMS),由瑞典MySQL AB公司开发,并在后来被Sun Microsystems收购,最终成为Oracle公司的一部分。MySQL广泛用于各种Web应用程序和大型企业应…...
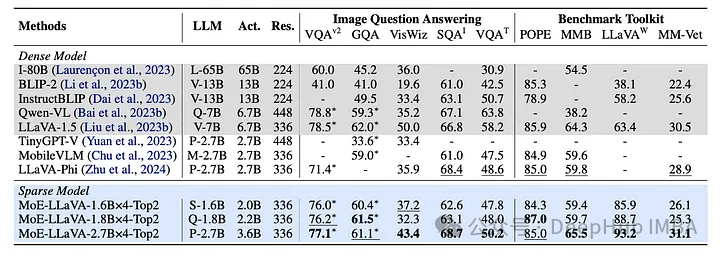
MoE-LLaVA:具有高效缩放和多模态专业知识的大型视觉语言模型
视觉和语言模型的交叉导致了人工智能的变革性进步,使应用程序能够以类似于人类感知的方式理解和解释世界。大型视觉语言模型(LVLMs)在图像识别、视觉问题回答和多模态交互方面提供了无与伦比的能力。 MoE-LLaVA利用了“专家混合”策略融合视觉和语言数据࿰…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
