【动态规划】【前缀和】【数学】2338. 统计理想数组的数目
作者推荐
【动态规划】【前缀和】【C++算法】LCP 57. 打地鼠
本文涉及知识点
动态规划汇总
C++算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频
LeetCode:2338. 统计理想数组的数目
给你两个整数 n 和 maxValue ,用于描述一个 理想数组 。
对于下标从 0 开始、长度为 n 的整数数组 arr ,如果满足以下条件,则认为该数组是一个 理想数组 :
每个 arr[i] 都是从 1 到 maxValue 范围内的一个值,其中 0 <= i < n 。
每个 arr[i] 都可以被 arr[i - 1] 整除,其中 0 < i < n 。
返回长度为 n 的 不同 理想数组的数目。由于答案可能很大,返回对 109 + 7 取余的结果。
示例 1:
输入:n = 2, maxValue = 5
输出:10
解释:存在以下理想数组:
- 以 1 开头的数组(5 个):[1,1]、[1,2]、[1,3]、[1,4]、[1,5]
- 以 2 开头的数组(2 个):[2,2]、[2,4]
- 以 3 开头的数组(1 个):[3,3]
- 以 4 开头的数组(1 个):[4,4]
- 以 5 开头的数组(1 个):[5,5]
共计 5 + 2 + 1 + 1 + 1 = 10 个不同理想数组。
示例 2:
输入:n = 5, maxValue = 3
输出:11
解释:存在以下理想数组: - 以 1 开头的数组(9 个):
- 不含其他不同值(1 个):[1,1,1,1,1]
- 含一个不同值 2(4 个):[1,1,1,1,2], [1,1,1,2,2], [1,1,2,2,2], [1,2,2,2,2]
- 含一个不同值 3(4 个):[1,1,1,1,3], [1,1,1,3,3], [1,1,3,3,3], [1,3,3,3,3]
- 以 2 开头的数组(1 个):[2,2,2,2,2]
- 以 3 开头的数组(1 个):[3,3,3,3,3]
共计 9 + 1 + 1 = 11 个不同理想数组。
提示:
2 <= n <= 104
1 <= maxValue <= 104
动态规划
令 m =maxValue
直接动态规划超时
dp[i][j]记录 长度为i,以j结尾的子序列数量。状态数:O(mn),每种状态转移的时间复杂度:O( m \sqrt m m)。约1010,超时。
预处理
vNext[i]包括x,表示x被i整除,且大于i,且<=maxValue。此部分的时间复杂度 和空间复杂度都是O(m m \sqrt {m} m)。
动态规划除重后的数量
除重后,最大长度14 {20,21 , ⋯ \cdots ⋯,2^13},令p= 14。
dp1[i][j] 记录除重后,长度为i,以j结尾的数量。空间复杂😮(qm) 转移所有dp[i]的时间复杂度:O(m m \sqrt {m} m),总时间复杂度:O(nm m \sqrt m m)
dp[0]忽略,dp[1][0]为0,其它为1。
通过前者状态更新后置状态。 F o r x : v N e x t [ j ] \Large For_{x:vNext[j]} Forx:vNext[j]dp[i][x] += dp[i][j]
动态规划
dp2[i][j] 从i个不同的数中选择j个数的选择数量,每个数至少选择一个。枚举后置状态。
d p [ i ] [ j ] = ∑ x : 1 j d p [ i − 1 ] [ j − x ] dp[i][j] =\sum _{x:1}^{j} dp[i-1][j-x] dp[i][j]=x:1∑jdp[i−1][j−x]
必须通过前缀和优化,否则时间复杂度😮(qnn),超时。
返回值
∑ x : 1 q ( ∑ ( d p 1 [ x ] ) ⋆ ( ∑ ( d p 2 [ x ] ) ) \sum _{x:1}^{q} (\sum(dp1[x])\star (\sum(dp2[x])) x:1∑q(∑(dp1[x])⋆(∑(dp2[x]))
代码
核心代码
template<int MOD = 1000000007>
class C1097Int
{
public:C1097Int(long long llData = 0) :m_iData(llData% MOD){}C1097Int operator+(const C1097Int& o)const{return C1097Int(((long long)m_iData + o.m_iData) % MOD);}C1097Int& operator+=(const C1097Int& o){m_iData = ((long long)m_iData + o.m_iData) % MOD;return *this;}C1097Int& operator-=(const C1097Int& o){m_iData = (m_iData + MOD - o.m_iData) % MOD;return *this;}C1097Int operator-(const C1097Int& o){return C1097Int((m_iData + MOD - o.m_iData) % MOD);}C1097Int operator*(const C1097Int& o)const{return((long long)m_iData * o.m_iData) % MOD;}C1097Int& operator*=(const C1097Int& o){m_iData = ((long long)m_iData * o.m_iData) % MOD;return *this;}bool operator<(const C1097Int& o)const{return m_iData < o.m_iData;}C1097Int pow(long long n)const{C1097Int iRet = 1, iCur = *this;while (n){if (n & 1){iRet *= iCur;}iCur *= iCur;n >>= 1;}return iRet;}C1097Int PowNegative1()const{return pow(MOD - 2);}int ToInt()const{return m_iData;}
private:int m_iData = 0;;
};class Solution {
public:int idealArrays(int n, int maxValue) {vector<vector<int>> vNext(maxValue + 1);for (int i = 1; i <= maxValue; i++){for (int j = i * 2; j <= maxValue; j += i){vNext[i].emplace_back(j);}}const int q = 14;vector<vector<C1097Int<> >> dp1(q + 1, vector<C1097Int<> >(maxValue + 1));dp1[1].assign(maxValue + 1,1);dp1[1][0] = 0;for (int i = 1; i < q; i++){for(int j = 0 ; j <= maxValue; j++ ){ for (const auto& next : vNext[j]){dp1[i + 1][next] += dp1[i][j];}}}vector<vector<C1097Int<> >> dp2(q + 1, vector<C1097Int<> >(n + 1));dp2[0][0] = 1;for (int i = 1; i <= q; i++){C1097Int biSum = dp2[i - 1][0];for (int j = 1; j <= n; j++){ dp2[i][j] = biSum;biSum += dp2[i - 1][j];}}C1097Int biRet;for (int i = 1; i <= q; i++){biRet += std::accumulate(dp1[i].begin(),dp1[i].end(),C1097Int())* dp2[i].back();}return biRet.ToInt();}
};
测试用例
template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{ int n, maxValue;{Solution sln;n = 2, maxValue = 5;auto res = sln.idealArrays(n, maxValue);Assert(res,10);}{Solution sln;n = 5, maxValue = 3;auto res = sln.idealArrays(n, maxValue);Assert(res, 11);}{Solution sln;n = 1000, maxValue = 1000;auto res = sln.idealArrays(n, maxValue);Assert(res, 91997497);}{Solution sln;n = 10000, maxValue = 10000;auto res = sln.idealArrays(n, maxValue);Assert(res, 22940607);}}
2023年2月
class Solution {
public:
int idealArrays(int n, int maxValue) {
m_n = n;
m_vPosNeedSel.assign(n + 1, vector(20, 0));
m_vPosNeedSel[1].assign(20,1);
for (int i = 2; i <= n; i++)
{
for (int j = 0; j < 20; j++)
{
//全部选择第一个位置
m_vPosNeedSel[i][j] += 1;
//第一个位置选择k个
for (int k = 0; k < j; k++)
{
m_vPosNeedSel[i][j] += m_vPosNeedSel[i - 1][j-k];
}
}
}
for (int i = 1; i <= maxValue; i++ )
{
Do(i);
}
return m_iRet.ToInt();
}
void Do(int i)
{
C1097Int aNum = 1 ;
for (int j = 2; j*j <= i; j++)
{
int iNumj = 0;
while (0 == i% j)
{
iNumj++;
i /= j;
}
aNum *= m_vPosNeedSel[m_n][iNumj];
}
if (i > 1)
{
aNum *= m_vPosNeedSel[m_n][1];
}
m_iRet += aNum;
}
vector<vector> m_vPosNeedSel;
int m_n;
C1097Int m_iRet = 0;
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【前缀和】【数学】2338. 统计理想数组的数目
作者推荐 【动态规划】【前缀和】【C算法】LCP 57. 打地鼠 本文涉及知识点 动态规划汇总 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 LeetCode:2338. 统计理想数组的数目 给你两个整数 n 和 maxValue ,用于描述一个 理想…...

【已解决】onnx转换为rknn置信度大于1,图像出现乱框问题解决
前言 环境介绍: 1.编译环境 Ubuntu 18.04.5 LTS 2.RKNN版本 py3.8-rknn2-1.4.0 3.单板 迅为itop-3568开发板 一、现象 采用yolov5训练并将pt转换为onnx,再将onnx采用py3.8-rknn2-1.4.0推理转换为rknn出现置信度大于1,并且图像乱框问题…...
多路服务器技术如何处理大量并发请求?
在当今的互联网时代,随着用户数量的爆炸性增长和业务规模的扩大,多路服务器技术已成为处理大量并发请求的关键手段。多路服务器技术是一种并行处理技术,它可以通过多个服务器同时处理来自不同用户的请求,从而显著提高系统的整体性…...

SpringBoot - 不加 @EnableCaching 标签也一样可以在 Redis 中存储缓存?
网上文章都是说需要在 Application 上加 EnableCaching 注解才能让缓存使用 Redis,但是测试发现不用 EnableCaching 也可以使用 Redis,是网上文章有问题吗? 现在 Application 上用了 EnableAsync,SpringBootApplication࿰…...
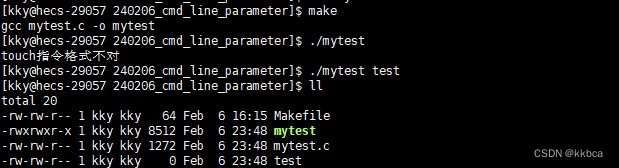
Linux------命令行参数
目录 前言 一、main函数的参数 二、命令行控制实现计算器 三、实现touch指令 前言 当我们在命令行输入 ls -al ,可以查看当前文件夹下所有文件的信息,还有其他的如rm,touch等指令,都可以帮我们完成相应的操作。 其实运行这些…...
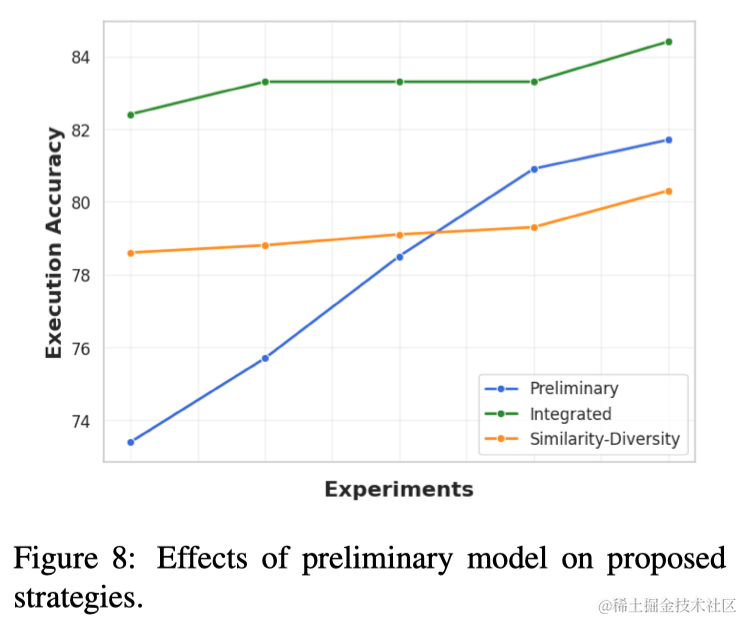
LLM少样本示例的上下文学习在Text-to-SQL任务中的探索
导语 本文探索了如何通过各种提示设计策略,来增强大型语言模型(LLMs)在Few-shot In-context Learning中的文本到SQL转换能力。通过使用示例SQL查询的句法结构来检索演示示例,并选择同时追求多样性和相似性的示例可以提高性能&…...
双非本科准备秋招(19.2)—— 设计模式之保护式暂停
一、wait & notify wait能让线程进入waiting状态,这时候就需要比较一下和sleep的区别了。 sleep vs wait 1) sleep 是 Thread 方法,而 wait 是 Object 的方法 2) sleep 不需要强制和 synchronized 配合使用,但 wait 强制和 s…...

使用SpringMVC实现功能
目录 一、计算器 1、前端页面 2、服务器处理请求 3、效果 二、用户登陆系统 1、前端页面 (1)登陆页面 (2)欢迎页面 2、前端页面发送请求--服务器处理请求 3、效果 三、留言板 1、前端页面 2、前端页面发送请求 &…...

spring aop实现接口超时处理组件
文章目录 实现思路实现代码starter组件 实现思路 这里使用FutureTask,它通过get方法以阻塞的方式获取执行结果,并设定超时时间: public V get() throws InterruptedException, ExecutionException ;public V get(long timeout, TimeUnit un…...
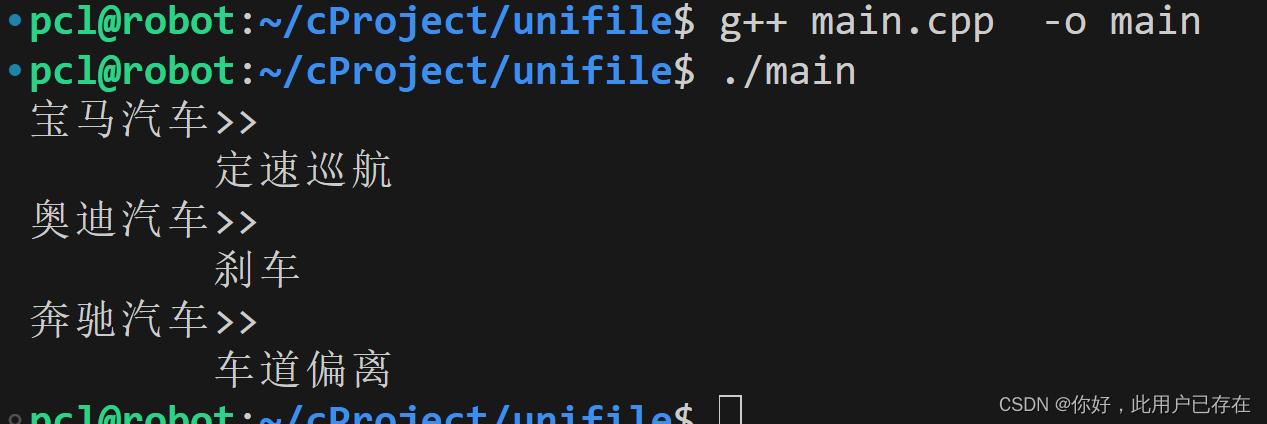
c++设计模式之装饰器模式
作用 为现有类增加功能 案例说明 class Car { public:virtual void show()0; };class Bmw:public Car { public:void show(){cout<<"宝马汽车>>"<<endl;} };class Audi:public Car { public:void show(){cout<<"奥迪汽车>>&q…...

WordPress如何实现随机显示一句话经典语录?怎么添加到评论框中?
我们在一些WordPress网站的顶部或侧边栏或评论框中,经常看到会随机显示一句经典语录,他们是怎么实现的呢? 其实,boke112百科前面跟大家分享的『WordPress集成一言(Hitokoto)API经典语句功能』一文中就提供…...

【退役之重学前端】vite, vue3, vue-router, vuex, ES6学习日记
学习使用vitevue3的所遇问题总结(2024年2月1日) 组件中使用<script>标签忘记加 setup 这会导致Navbar 没有暴露出来,导致使用不了,出现以下报错 这是因为,如果不用setup,就得使用 export default…...

[linux]-总线,设备,驱动,dts
1. 总线BUS 在物理层面上,代表不同的工作时序和电平特性: 总线代表着同类设备需要共同遵守的工作时序,不同的总线对于物理电平的要求是不一样的,对于每个比特的电平维持宽度也是不一样,而总线上传递的命令也会有自己…...

python3实现gitlab备份文件上传腾讯云COS
gitlab备份文件上传腾讯云COS 脚本说明脚本名称:upload.py 假设gitlab备份文件目录:/opt/gitlab/backups gitlab备份文件格式:1706922037_2024_02_06_14.2.1_gitlab_backup.tar1.脚本需和gitlab备份文件同级目录 2.根据备份文件中的日期判断…...

292.Nim游戏
桌子上有一堆石头。 轮流进行自己的回合, 你作为先手 。 每一回合,轮到的人拿掉 1 - 3 块石头。 拿掉最后一块石头的人就是获胜者。 假设你们每一步都是最优解。请编写一个函数,来判断你是否可以在给定石头数量为 n 的情况下赢得游戏。如果可…...
Spring和Spring Boot的区别
Spring 是一个轻量级的 Java 开发框架,它提供了一系列的模块和功能,例如 IoC(控制反转)、AOP(面向方面编程)、数据库访问、Web 开发等。Spring 的目标是使 Java 开发更加简单、高效和可维护。 Spring Boot …...

备战蓝桥杯---动态规划(理论基础)
目录 动态规划的概念: 解决多阶段决策过程最优化的一种方法 阶段: 状态: 决策: 策略: 状态转移方程: 适用的基本条件 1.具有相同的子问题 2.满足最优子结构 3.满足无后效性 动态规划的实现方式…...
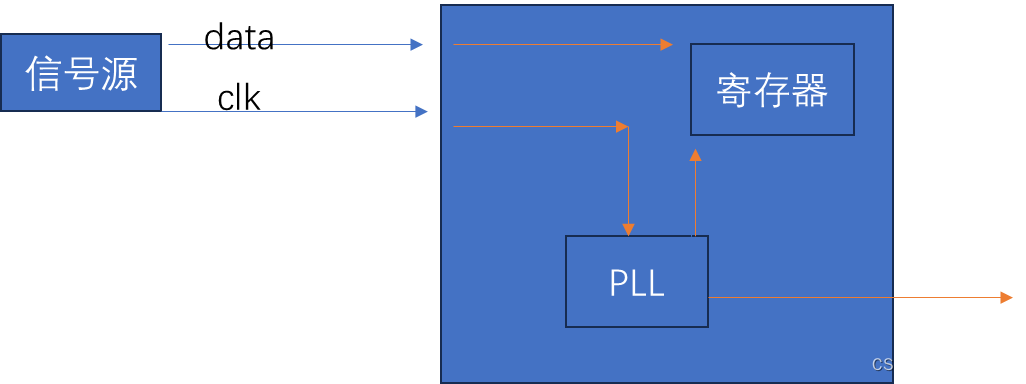
FPGA_ip_pll
常使用插件管理器进行ip核的配置,ip核分为计算,存储,输入输出,视频图像处理,接口,调试等。 一 pll ip核简介 pll 即锁相环,可以对输入到fpga的时钟信号,进行分频,倍频&…...

【实验3】统计某电商网站买家收藏商品数量
文章目录 一、实验目的和要求∶二、实验任务∶三、实验准备方案,包括以下内容:实验内容一、实验环境二、实验内容与步骤(过程及数据记录):三、实验结果分析、思考题解答∶四、感想、体会、建议∶一、实验目的和要求∶ 现有某电商网站用户对商品的收藏数据,记录了用户收藏…...
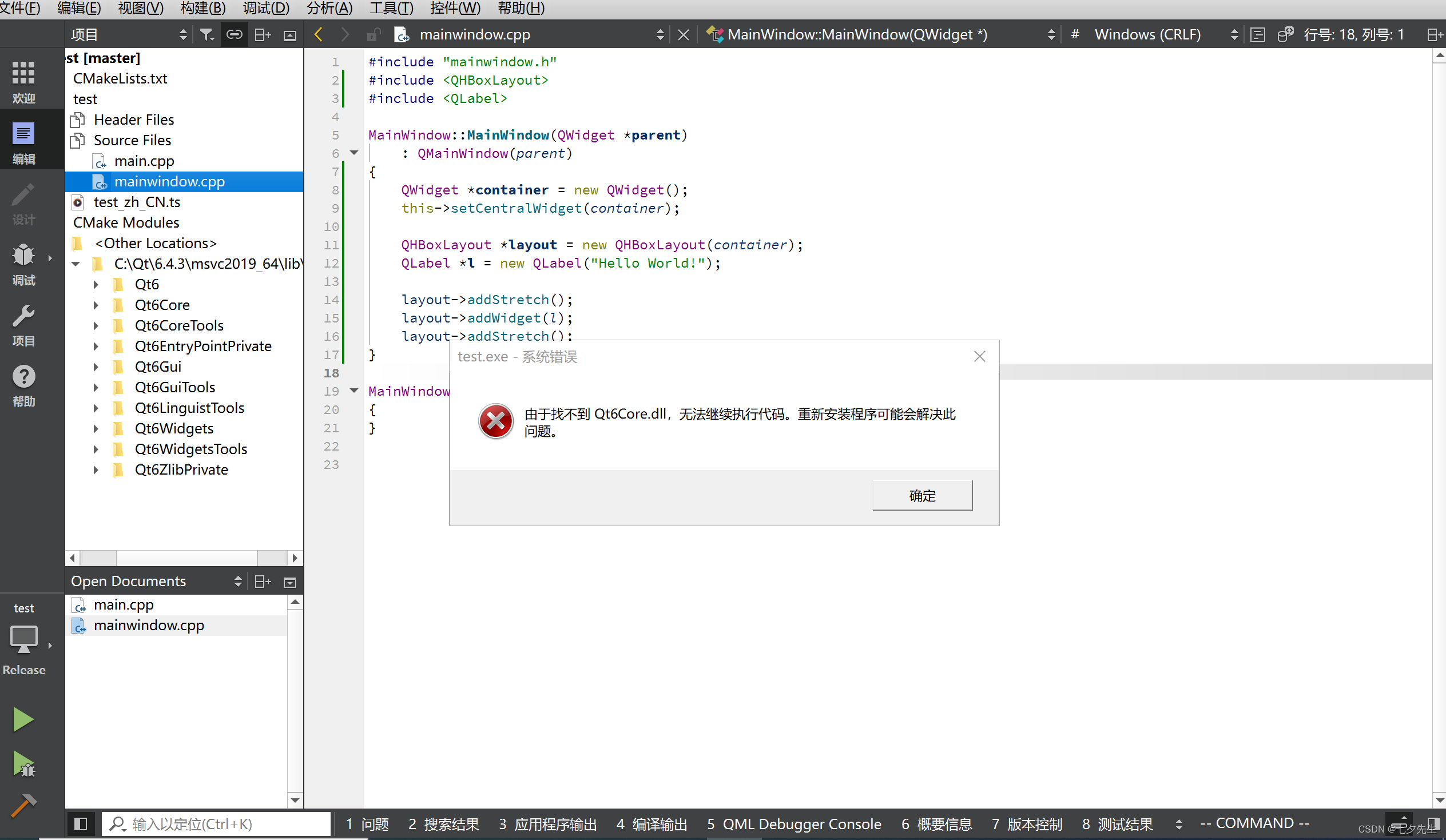
【Qt】Android上运行keeps stopping, Desktop上正常
文章目录 问题 & 背景背景问题 解决方案One More ThingTake Away 问题 & 背景 背景 在文章【Qt】最详细教程,如何从零配置Qt Android安卓环境中,我们在Qt中配置了安卓开发环境,并且能够正常运行。 但笔者在成功配置并完成上述文章…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
