移动最小二乘法
移动最小二乘法(Moving Least Square,MLS)主要应用于曲线与曲面拟合,该方法基于紧支撑加权函数(即函数值只在有限大小的封闭域中定义大于零,而在域外则定义为零)和多项式基函数,通过加权最小二乘法建立适合散点(Scattered points)模型的拟合函数。其主要特点是:
- 不需对拟合和插值区域进行划分,只需散点模型;
- 由于 MLS 引入了紧支撑权函数,因此具有局部拟合或插值特点。
- 改变基函数的多项式次数可以方便地控制曲线曲面拟合或插值精度,改变权函数可以改变曲线曲面的光滑度。
一、移动最小二乘法原理
曲线与曲面拟合是寻找一个相对简单的函数来逼近一个数据集的过程。通过按距离加权的方法计算近似函数值和给定数据值的差的平方和来度量拟合的性能,这就是加权最小二乘法的基本思想。移动最小二乘法的提出是对传统加权最小二乘方法更一般性的推广。并特别强调加权函数的紧支撑性,因此具有局部数值分析的特点。
在拟合区域的一个局部子域上,假设需要拟合的函数 F ( x ) F(x) F(x) 的近似函数 F ^ ( x ) \hat{F}(x) F^(x)可表达为
F ^ ( x ) = ∑ j = 1 m b j ( x ) a j ( x ) = b T ( x ) a T ( x ) (1) \hat{F}(x)=\sum_{j=1}^mb_j(x)a_j(x)=\pmb{b^T(x)a^T(x)}\tag{1} F^(x)=j=1∑mbj(x)aj(x)=bT(x)aT(x)(1)
这里 m m m 是基函数的项数, b j ( x ) b_j(x) bj(x) 是基函数, a j ( x ) a_j(x) aj(x) 是其系数。假定基函数 b j ( x ) b_j(x) bj(x) 是多项式,则具有如下形式:
一次多项式(线性基)
{ b T = ( 1 , x ) 1 D b T = ( 1 , x , y ) 2 D \begin{cases} \pmb{b^T}=(1,x)\quad &1D\\[2ex] \pmb{b^T}=(1,x,y)&2D \end{cases} ⎩ ⎨ ⎧bT=(1,x)bT=(1,x,y)1D2D
二次多项式(二次基)
{ b T = ( 1 , x , x 2 ) 1 D b T = ( 1 , x , y , x 2 , x y , y 2 ) 2 D \begin{cases} \pmb{b^T}=(1,x,x^2)\quad &1D\\[2ex] \pmb{b^T}=(1,x,y,x^2,xy,y^2)&2D \end{cases} ⎩ ⎨ ⎧bT=(1,x,x2)bT=(1,x,y,x2,xy,y2)1D2D
立方基
{ b T = ( 1 , x , x 2 , x 3 ) 1 D b T = ( 1 , x , y , x 2 , x y , y 2 , x 3 , x 2 y , x y 2 , y 3 ) 2 D \begin{cases} \pmb{b^T}=(1,x,x^2,x^3)\quad &1D\\[2ex] \pmb{b^T}=(1,x,y,x^2,xy,y^2,x^3,x^2y,xy^2,y^3)&2D \end{cases} ⎩ ⎨ ⎧bT=(1,x,x2,x3)bT=(1,x,y,x2,xy,y2,x3,x2y,xy2,y3)1D2D
由(1)式,利用加权最小二乘方法构成二次形式
J = ∑ i = 1 n w ( x − x i ) [ ∑ j = 1 m b j ( x i ) a j ( x ) − f i ] 2 (2) J=\sum_{i=1}^nw(x-x_i)\Big[\sum_{j=1}^mb_j(x_i)a_j(x)-f_i\Big]^2\tag{2} J=i=1∑nw(x−xi)[j=1∑mbj(xi)aj(x)−fi]2(2)
这里 n n n 是 x x x 附近的影响节点数。 w ( x − x i ) w(x-x_i) w(x−xi) 是节点 x i x_i xi 具有紧支撑性质的光滑连续权函数,在 x i x_i xi 紧支持域内部, w i = w ( x − x i ) > 0 w_i=w(x-x_i)>0 wi=w(x−xi)>0,在其边界和外部 w i = 0 w_i=0 wi=0。 f i f_i fi 是 x i x_i xi 节点值。
式(2)对系数 a ( x ) a(x) a(x) 求导得
∂ J ∂ a j = 2 ∑ i = 1 n b k ( x i ) w ( x − x i ) [ ∑ j = 1 m b j ( x i ) a j ( x ) − f i ] = 0 (3) \frac{\partial J}{\partial a_j}=2\sum_{i=1}^nb_k(x_i)w(x-x_i)\Big[\sum_{j=1}^mb_j(x_i)a_j(x)-f_i\Big]=0\tag{3} ∂aj∂J=2i=1∑nbk(xi)w(x−xi)[j=1∑mbj(xi)aj(x)−fi]=0(3)
上式写成
A ( x ) a ( x ) = D ( x ) f (4) \pmb{A(x)a(x)=D(x)f}\tag{4} A(x)a(x)=D(x)f(4)
则
a ( x ) = A − 1 ( x ) D ( x ) f (5) \pmb{a(x)=A^{-1}(x)D(x)f}\tag{5} a(x)=A−1(x)D(x)f(5)
其中, A = B T W ( x ) B , D = B T W ( x ) \pmb{A=B^TW(x)B,\quad D=B^TW(x)} A=BTW(x)B,D=BTW(x)
其中,
B = [ b 1 ( x 1 ) b 2 ( x 1 ) ⋯ b m ( x 1 ) b 1 ( x 2 ) b 2 ( x 2 ) ⋯ b m ( x 2 ) ⋮ ⋮ ⋮ b 1 ( x n ) b 2 ( x n ) ⋯ b m ( x n ) ] W ( x ) = [ w ( x − x 1 ) 0 ⋯ 0 0 w ( x − x 2 ) ⋯ 0 ⋮ ⋮ ⋮ 0 0 ⋯ w ( x − x n ) ] \pmb{B}=\left[\begin{matrix} b_1(x_1) &b_2(x_1) &\cdots &b_m(x_1)\\ b_1(x_2) &b_2(x_2) &\cdots &b_m(x_2)\\ \vdots &\vdots & &\vdots\\ b_1(x_n) &b_2(x_n) &\cdots &b_m(x_n)\\ \end{matrix}\right]\\[3ex] \pmb{W(x)}=\left[\begin{matrix} w(x-x_1) &0 &\cdots &0\\ 0 &w(x-x_2) &\cdots &0\\ \vdots &\vdots & &\vdots\\ 0 &0 &\cdots &w(x-x_n)\\ \end{matrix}\right] B= b1(x1)b1(x2)⋮b1(xn)b2(x1)b2(x2)⋮b2(xn)⋯⋯⋯bm(x1)bm(x2)⋮bm(xn) W(x)= w(x−x1)0⋮00w(x−x2)⋮0⋯⋯⋯00⋮w(x−xn)
将(5)式代入(1)式, F ^ ( x ) \hat{F}(x) F^(x) 可表达为:
F ^ ( x ) = b T A − 1 ( x ) D ( x ) f \hat{F}(x)=\pmb{b^TA^{-1}(x)D(x)f} F^(x)=bTA−1(x)D(x)f
特别地当基函数为常数即 b = 1 b=1 b=1 时,
J = ∑ i = 1 n w ( x − x i ) [ a 1 − f i ] 2 J=\sum_{i=1}^nw(x-x_i)[a_1-f_i]^2 J=i=1∑nw(x−xi)[a1−fi]2
J J J 对 a 1 a_1 a1 求导,令其为 0:
∂ J ∂ a 1 = 2 ∑ i = 1 n w ( x − x i ) [ a 1 − f i ] = 0 \frac{\partial J}{\partial a_1}=2\sum_{i=1}^nw(x-x_i)[a_1-f_i]=0 ∂a1∂J=2i=1∑nw(x−xi)[a1−fi]=0
求得
a 1 = ∑ i = 1 n w ( x − x i ) f i ∑ i = 1 n w ( x − x i ) a_1=\dfrac{\sum_{i=1}^nw(x-x_i)f_i}{\sum_{i=1}^nw(x-x_i)} a1=∑i=1nw(x−xi)∑i=1nw(x−xi)fi
所以
F ^ ( x ) = ∑ i = 1 n w ( x − x i ) f i ∑ i = 1 n w ( x − x i ) \hat{F}(x)=\dfrac{\sum_{i=1}^nw(x-x_i)f_i}{\sum_{i=1}^nw(x-x_i)} F^(x)=∑i=1nw(x−xi)∑i=1nw(x−xi)fi
二、紧支撑权函数
移动最小二乘法曲线曲面拟合或插值计算中,权函数在其中具有非常重要的作用。这里的权函数必须具有紧支撑性,使其有能力在处理大规模曲线与曲面拟合时局部修改更容易。紧支撑权函数的选择应遵循几个原则:
- 每点的权函数值在紧支撑域内是大于零的正数,而在该点紧支撑域边界和外部为零;
- 必须具有单位分解性;
- 权函数必须光滑连续可导;
- 在支撑域内愈远离该点,权值愈小,即保证权值与距离成反比关系。
(1)紧支撑域及生成算法
紧支撑权函数的引入导致移动最少二乘法具有局部拟合或插值性质,大大提高了计算效率和规模。MLS 进行局部拟合或插值时,参与局部拟合或插值的相邻节点对 “计算点” 的影响是由给定拟合或插值节点的局部紧支撑域决定。
MLS 近似计算之前先要生成每个节点的局部紧支撑域,一个节点的局部紧支撑域形状可以是 “圆” ,“椭圆” 或 “矩形” 等,下面以 “圆” 紧支撑域为例,说明如何由离散节点模型自动形成各节点的紧支撑域。该算法确定 N 个节点的离散模型的紧支撑域。
紧支撑域形成算法:
- 赋 N 个节点的每一个 “圆” 紧支撑域的大小 h i = 0 h_i=0 hi=0;
- 以每个节点为原点,确定各象限与该点距离最近的点,其自动计算得到 4 个象限内的距离分别为 h i 1 、 h i 2 、 h i 3 、 h i 4 h_{i1}、h_{i2}、h_{i3}、h_{i4} hi1、hi2、hi3、hi4 确定 h i = max { h i 1 , h i 2 , h i 3 , h i 4 } h_i=\max\{h_{i1},h_{i2},h_{i3},h_{i4}\} hi=max{hi1,hi2,hi3,hi4};保证紧支持域包含各个方向合适的节点,如图所示。循环 N 个节点;
- 引入紧支撑域大小的影响系数 β \beta β,每个节点 h i h_i hi 乘系数 β \beta β,根据实际情况适当扩大紧支撑域大小以提高拟合或插值精度,一般取 β = 1.2 ∼ 2.5 \beta=1.2\sim 2.5 β=1.2∼2.5。
上面算法称为四象限法则,每个节点支撑域的大小由该法则确定。

移动最小二乘法中,权函数紧支撑域大小选取要合适,既要保证所有离散节点的支撑域形成对拟合或插值全域的覆盖,又要使域内需拟合或插值 “计算点” 有足够多的邻近节点覆盖以保证精度和使 A A A 矩阵可逆从而使 MLS 算法可行。当选取线性基函数时,曲线拟合影响节点不得小于 2 个,曲面拟合影响节点不得少于不在同直线上的 3 个节点。
(2)‘‘计算点” 的影响节点确定
拟合(或插值)域内任意一点往往同时处于好几个节点的支撑域相交部分。如图所示, x 1 , x 2 , x 3 , x 4 , x 5 x_1,x_2,x_3,x_4,x_5 x1,x2,x3,x4,x5 的支撑域均覆盖住 “计算点 x x x”,即计算 “计算点” 时需考虑这五个节点的影响(通常称为 “计算点 x x x” 的影响节点),该 “计算点” 的函数值及其导数值的计算皆需以此作为依据进行拟合或插值。图中 x 6 x_6 x6 点的支撑域大小(如图中的 “虚线圆” )不能盖住 “计算点 x x x ”,因此不参与 “计算点 x x x ” 的相关计算。

三、基函数的正交化
多项式基函数的项数选取越多,则矩阵 A A A 阶数越高,其求逆就越费时。随着 “计算点” 的增多,每点的 A A A 矩阵不同,皆需求逆,计算量很大。因此,为了避免方程中 A A A 的求逆,减少计算量,可以利用 Schmidt 正交化过程由基函数 b j ( x ) , j = 1 , ⋯ , m b_j(x),\quad j=1,\cdots,m bj(x),j=1,⋯,m 构造正交形式的基函数 q j ( x ) , j = 1 , ⋯ , m q_j(x),\quad j=1,\cdots,m qj(x),j=1,⋯,m,由此得到的 A A A 矩阵将是对角矩阵。基函数的正交化不仅避免了矩阵 A A A 的求逆,而且可以避免可能出现的病态矩阵。
Schmidt 正交化过程
首先因为基函数系数 a ( x ) a(x) a(x) 的 x x x 和 b ( x ) b(x) b(x) 中的 x x x 意义不同,所以在正交化过程和最小二乘中区分两个 x x x 非常必要。以下将 a ( x ) a(x) a(x) 的 x x x 记为 x ˉ \bar{x} xˉ, b ( x ) b(x) b(x) 中的 x x x 记为 x x x。
对给定的多项式基函数 b j ( x ) , j = 1 , ⋯ , m b_j(x),\quad j=1,\cdots,m bj(x),j=1,⋯,m,存在正交形式的基函数 q j ( x , x ˉ ) , j = 1 , ⋯ , m q_j(x,\bar{x}),\quad j=1,\cdots,m qj(x,xˉ),j=1,⋯,m,并且
q 1 ( x , x ˉ ) = b 1 ( x ) q j ( x , x ˉ ) = b j ( x ) − ∑ J = 1 j − 1 α j J ( x ˉ ) q J ( x , x ˉ ) , j = 2 , ⋅ , m q_1(x,\bar{x})=b_1(x)\\ q_j(x,\bar{x})=b_j(x)-\sum_{J=1}^{j-1}\alpha_{jJ}(\bar{x})q_J(x,\bar{x}),\quad j=2,\cdot,m q1(x,xˉ)=b1(x)qj(x,xˉ)=bj(x)−J=1∑j−1αjJ(xˉ)qJ(x,xˉ),j=2,⋅,m
其中
α j J = ∑ i = 1 n w i ( x ˉ ) b j ( x i ) q J ( x i , x ˉ ) ∑ j = 1 n w i ( x ˉ ) q J 2 ( x i , x ˉ ) \alpha_{jJ}=\frac{\sum_{i=1}^nw_i(\bar{x})b_j(x_i)q_J(x_i,\bar{x})}{\sum_{j=1}^nw_i(\bar{x})q_J^2(x_i,\bar{x})} αjJ=∑j=1nwi(xˉ)qJ2(xi,xˉ)∑i=1nwi(xˉ)bj(xi)qJ(xi,xˉ)
一维情况下的正交基函数为:
{ q 0 ( x , x ˉ ) = 1 q 1 ( x , x ˉ ) = x − α 1 q k + 1 ( x , x ˉ ) = ( x − α k + 1 ) q k ( x , x ˉ ) − β k + 1 q k − 1 ( x , x ˉ ) α k + 1 ( x ˉ ) = ( x q k , q k ) ( q k , q k ) = ∑ i = 1 m w i ( x ˉ ) x i q k 2 ( x i , x ˉ ) ∑ i = 1 m w i ( x ˉ ) q k 2 ( x i , x ˉ ) β k + 1 ( x ˉ ) = ( q k , q k ) ( q k − 1 , q k − 1 ) = ∑ i = 1 m w i ( x ˉ ) q k 2 ( x i , x ˉ ) ∑ i = 1 m w i ( x ˉ ) q k − 1 2 ( x i , x ˉ ) \begin{cases} q_0(x,\bar{x})=1\\[1ex] q_1(x,\bar{x})=x-\alpha_1\\[1ex] q_{k+1}(x,\bar{x})=(x-\alpha_{k+1})q_k(x,\bar{x})-\beta_{k+1}q_{k-1}(x,\bar{x})\\[1ex] \alpha_{k+1}(\bar{x})=\dfrac{(xq_k,q_k)}{(q_k,q_k)}=\dfrac{\sum_{i=1}^mw_i(\bar x)x_iq_k^2(x_i,\bar x)}{\sum_{i=1}^mw_i(\bar x)q_k^2(x_i,\bar x)}\\[3ex] \beta_{k+1}(\bar x)=\dfrac{(q_k,q_k)}{(q_{k-1},q_{k-1})}=\dfrac{\sum_{i=1}^mw_i(\bar x)q_k^2(x_i,\bar x)}{\sum_{i=1}^mw_i(\bar x)q_{k-1}^2(x_i,\bar x)} \end{cases} ⎩ ⎨ ⎧q0(x,xˉ)=1q1(x,xˉ)=x−α1qk+1(x,xˉ)=(x−αk+1)qk(x,xˉ)−βk+1qk−1(x,xˉ)αk+1(xˉ)=(qk,qk)(xqk,qk)=∑i=1mwi(xˉ)qk2(xi,xˉ)∑i=1mwi(xˉ)xiqk2(xi,xˉ)βk+1(xˉ)=(qk−1,qk−1)(qk,qk)=∑i=1mwi(xˉ)qk−12(xi,xˉ)∑i=1mwi(xˉ)qk2(xi,xˉ)
( 令 β 1 = 0 \beta_1=0 β1=0 ),其中
k = 0 , 1 , ⋯ , m − 1 k=0,1,\cdots,m-1 k=0,1,⋯,m−1
由(2.3)式可知:
∑ i = 1 n w i ( x ˉ ) ∑ j = 1 m b k ( x i ) b j ( x i ) a j ( x ˉ ) = ∑ i = 1 n w i ( x ˉ ) b k ( x i ) f i ∑ k , j = 1 m ( ∑ i = 1 n ( w i ( x ˉ ) b k ( x i ) b j ( x i ) ) ) a j ( x ˉ ) = ∑ i = 1 n w i ( x ˉ ) b k ( x i ) f i (6) \sum_{i=1}^nw_i(\bar x)\sum_{j=1}^mb_k(x_i)b_j(x_i)a_j(\bar x)=\sum_{i=1}^nw_i(\bar x)b_k(x_i)f_i\\ \sum_{k,j=1}^m\Big(\sum_{i=1}^n(w_i(\bar x)b_k(x_i)b_j(x_i))\Big)a_j(\bar x)=\sum_{i=1}^nw_i(\bar x)b_k(x_i)f_i\tag{6} i=1∑nwi(xˉ)j=1∑mbk(xi)bj(xi)aj(xˉ)=i=1∑nwi(xˉ)bk(xi)fik,j=1∑m(i=1∑n(wi(xˉ)bk(xi)bj(xi)))aj(xˉ)=i=1∑nwi(xˉ)bk(xi)fi(6)
由加权正交基定义
( b k , b j ) = ∑ i = 1 n w i ( x ˉ ) b k ( x i ) b j ( x i ) ( b k , f ) = ∑ i = 1 n w i ( x ˉ ) b k ( x i ) f i (b_k,b_j)=\sum_{i=1}^nw_i(\bar x)b_k(x_i)b_j(x_i)\\ (b_k,f)=\sum_{i=1}^nw_i(\bar x)b_k(x_i)f_i (bk,bj)=i=1∑nwi(xˉ)bk(xi)bj(xi)(bk,f)=i=1∑nwi(xˉ)bk(xi)fi
因此式(6)表示为
∑ j = 1 m ( b k , b j ) a j ( x ) = ( b k , f ) k , j = 1 , ⋯ , m \sum_{j=1}^m(b_k,b_j)a_j(x)=(b_k,f)\quad k,j=1,\cdots,m j=1∑m(bk,bj)aj(x)=(bk,f)k,j=1,⋯,m
( b k , b j ) (b_k,b_j) (bk,bj) 生成的矩阵是满阵,可以通过 Schmidt 正交化中的正交基函数 q j ( x ) ( j = 1 , ⋯ , m ) q_j(x)\ (j=1,\cdots,m) qj(x) (j=1,⋯,m) 将其对角化。由正交基的性质得到
F ^ ( x ) = ∑ j = 1 m q j ( x , x ˉ ) a j ( x ˉ ) \hat{F}(x)=\sum_{j=1}^mq_j(x,\bar x)a_j(\bar x) F^(x)=j=1∑mqj(x,xˉ)aj(xˉ)
由此推得:
∑ j = 1 m ( q k , q j ) a j ( x ) = ( q k , f ) \sum_{j=1}^m(q_k,q_j)a_j(x)=(q_k,f) j=1∑m(qk,qj)aj(x)=(qk,f)
因为
( q k , q j ) = { 0 k ≠ j ≠ 0 k = j (q_k,q_j)= \begin{cases} 0\quad & k\neq j\\ \neq 0 &k=j \end{cases} (qk,qj)={0=0k=jk=j
矩阵 A A A 是对角矩阵, a j ( x ) a_j(x) aj(x) 的求解无需求逆,即
a j ( x ˉ ) = ( q j , f ) ( q j , q j ) = ∑ i = 1 n w i ( x ˉ ) q j ( x i , x ˉ ) f i ∑ i = 1 n w i ( x ˉ ) q j 2 ( x i , x ˉ ) a_j(\bar x)=\dfrac{(q_j,f)}{(q_j,q_j)}=\dfrac{\sum_{i=1}^nw_i(\bar x)q_j(x_i,\bar x)f_i}{\sum_{i=1}^nw_i(\bar x)q_j^2(x_i,\bar x)} aj(xˉ)=(qj,qj)(qj,f)=∑i=1nwi(xˉ)qj2(xi,xˉ)∑i=1nwi(xˉ)qj(xi,xˉ)fi
令 d i ( x ˉ ) = ∑ i = 1 n w i ( x ˉ ) q j 2 ( x i , x ˉ ) d_i(\bar x)=\sum_{i=1}^nw_i(\bar x)q_j^2(x_i,\bar x) di(xˉ)=i=1∑nwi(xˉ)qj2(xi,xˉ)
x , x ˉ x,\quad \bar x x,xˉ 的区分只是最小二乘法过程需要,这一过程完成后,就不再有区分的必要,最终得到
F ^ ( x ) = ∑ i = 1 n φ i f i φ i = w i ( x ) ∑ j = 1 m q j ( x i , x ) q j ( x i , x ) d i ( x ) \hat{F}(x)=\sum_{i=1}^n\varphi_if_i\\ \varphi_i=w_i(x)\sum_{j=1}^m\frac{q_j(x_i,x)q_j(x_i,x)}{d_i(x)} F^(x)=i=1∑nφifiφi=wi(x)j=1∑mdi(x)qj(xi,x)qj(xi,x)
当基函数次数增加时,只需要计算 a m + 1 a_{m+1} am+1 以及 Schmidt 正交化过程中的 α m + 1 \alpha_{m+1} αm+1 和 β m + 1 \beta_{m+1} βm+1 即可,不需要重新计算矩阵 A A A 中所有元素,减少了计算量,降低了误差。
相关文章:

移动最小二乘法
移动最小二乘法(Moving Least Square,MLS)主要应用于曲线与曲面拟合,该方法基于紧支撑加权函数(即函数值只在有限大小的封闭域中定义大于零,而在域外则定义为零)和多项式基函数,通过…...

【LeetCode】37. 解数独(困难)——代码随想录算法训练营Day30
题目链接:37. 解数独 题目描述 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&…...

VUE学习——属性绑定
属性绑定,就是给html添加id、class这样类似的操作。 <template><div v-bind:id"dynamicId"><div v-bind:class"dynamicClass">Test</div></div> </template><script>export default{data(){return{…...
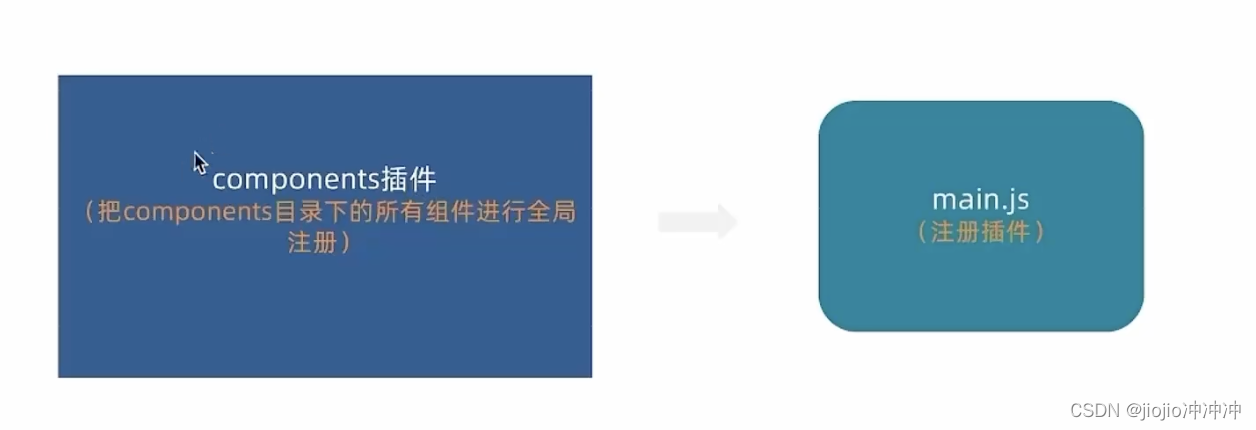
vue3 之 通用组件统一注册全局
components/index.js // 把components中的所组件都进行全局化注册 // 通过插件的方式 import ImageView from ./ImageView/index.vue import Sku from ./XtxSku/index.vue export const componentPlugin {install (app) {// app.component(组件名字,组件配置对象)…...
[Java][算法 双指针]Day 02---LeetCode 热题 100---04~07
LeetCode 热题 100---04~07 第一题:移动零 思路 找到每一个为0的元素 然后移到数组的最后 但是需要注意的是 要在给定的数组原地进行修改 并且其他非零元素的相对顺序不能改变 我们采用双指针法 定义两个指针i和j i和j一开始分别都在0索引位置 然后判断j所…...

【问题解决】如何将一个服务器的docker迁移到另一个服务器
要将Docker容器从一台机器迁移到另一台机器,可以按照以下步骤操作: 在机器A上提交容器为镜像: 使用docker commit命令将运行中的容器保存为新的镜像。这里需要容器的ID或名称,以及你想要命名的目标镜像名。 docker commit [容器…...

C++单例模式详解
目录 0. 前言 1. 懒汉式单例模式 1.1 最简单的单例模式 1.2 防止内存泄漏 1.2.1 智能指针的方法 1.2.2 静态嵌套的方法 1.3 保证线程安全 1.4 C11版本的优雅解决方案 2. 饿汉式单例模式 0. 前言 起因是在程序中重复声明了一个单例模式的变量,后来程序怎么调…...
LLM应用开发与落地:流式响应
一、背景 最近智能客服产品给到一个游戏客户那边,客户那边的客服负责人体验后认为我们产品回答的准确率是还是比较高的。同时,他反馈了几个需要改进的地方,其中一个就是机器人回复慢。机器人回复慢有很多原因,也有优化方式&#…...
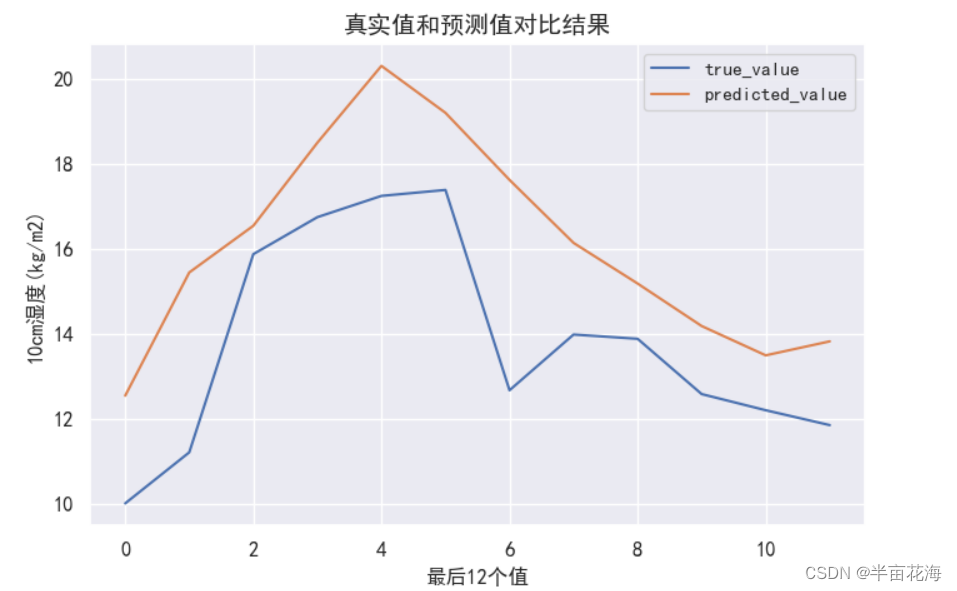
神经网络 | 基于 CNN 模型实现土壤湿度预测
Hi,大家好,我是半亩花海。在现代农业和环境监测中,了解土壤湿度的变化对于作物生长和水资源管理至关重要。通过深度学习技术,特别是卷积神经网络,我们可以利用过去的土壤湿度数据来预测未来的湿度趋势。本文将使用 Pad…...
江科大STM32 终
目录 SPI协议10.1 SPI简介W25Q64简介10.3 SPI软件读写W25Q6410.4 SPI硬件外设读写W25Q64 BKP备份寄存器、PER电源控制器、RTC实时时钟11.0 Unix时间戳代码示例:读写备份寄存器BKP11.2 RTC实时时钟 十二、PWR电源控制12.1 PWR简介代码示例:修改主频12.3 串…...

《MySQL 简易速速上手小册》第10章:未来趋势和进阶资源(2024 最新版)
文章目录 10.1 MySQL 在云计算和容器化中的应用10.1.1 基础知识10.1.2 重点案例:使用 Python 部署 MySQL 到 Kubernetes10.1.3 拓展案例 1:在 AWS RDS 上部署 MySQL 实例10.1.4 拓展案例 2:使用 Docker 部署 MySQL 10.2 MySQL 和 NoSQL 的整合…...

Stable Diffusion 模型下载:GhostMix(幽灵混合)
文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十 下载地址 模型介绍 GhostMix 是绝对让你惊艳的模型,也是自己认为现在最强的2.5D模型。我认为模型的更新应该是基于现有的画面整体不大变的前提下,提高模型的成…...

django解决Table ‘xx‘ already exists的方法
1,首先看已存在的这个库表结构是什么样的,先让对应的model.py恢复到和他一样的字段 2,删除对应app下的migrations目录里面除__init__.py文件的其他所有文件 3,回到manage.py所在目录执行python manage.py makemigrations 4&#x…...

qt学习:arm摄像头+c调用v412框架驱动+qt调用v412框架驱动 显示摄像头画面
目录 跟内核进行数据通信的函数 编程步骤 c代码 头文件 打开摄像头文件 /dev/videox 获取当前主机上(开发板)摄像头列表信息 设置当前摄像头的画面格式 比如说 设置 采集图像的宽度为640 高度 480 在内核空间中,申请一个缓冲区队列…...
Linux 36.2@Jetson Orin Nano基础环境构建
Linux 36.2Jetson Orin Nano基础环境构建 1. 源由2. 步骤2.1 安装NVIDIA Jetson Linux 36.2系统2.2 必备软件安装2.3 基本远程环境2.3.1 远程ssh登录2.3.2 samba局域网2.3.3 VNC远程登录 2.4 开发环境安装 3. 总结 1. 源由 现在流行什么,也跟风来么一个一篇。当然&…...
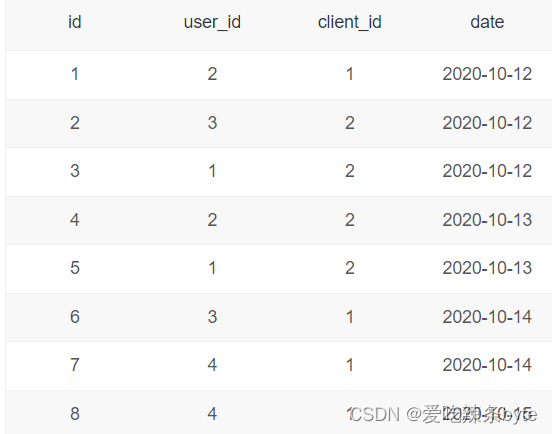
牛客网SQL264:查询每个日期新用户的次日留存率
官网链接: 牛客每个人最近的登录日期(五)_牛客题霸_牛客网牛客每天有很多人登录,请你统计一下牛客每个日期新用户的次日留存率。 有一个登录(login。题目来自【牛客题霸】https://www.nowcoder.com/practice/ea0c56cd700344b590182aad03cc61b8?tpId82 …...
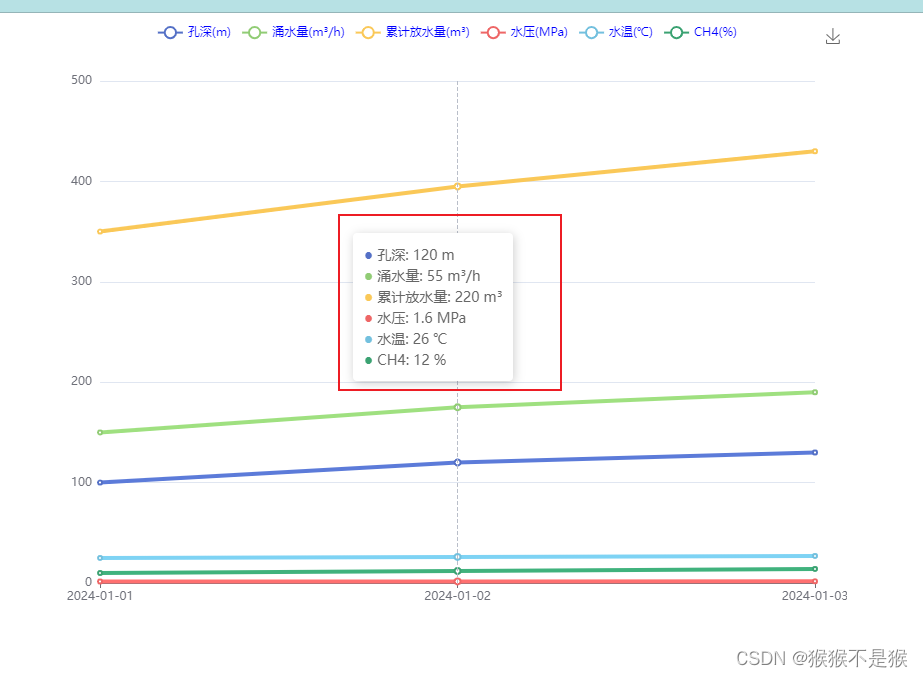
echarts 曲线图自定义提示框
<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>曲线图</title><!-- 引入 ECharts 库 -->…...
幻兽帕鲁服务器怎么搭建?Palworld多人联机教程
玩转幻兽帕鲁服务器,阿里云推出新手0基础一键部署幻兽帕鲁服务器教程,傻瓜式一键部署,3分钟即可成功创建一台Palworld专属服务器,成本仅需26元,阿里云服务器网aliyunfuwuqi.com分享2024年新版基于阿里云搭建幻兽帕鲁服…...
DAY39: 动态规划不同路径问题62
Leetcode: 62 不同路径 机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。 基本思路 1、确定dp数组(dp table)以及下标的含义 dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条…...
idea开发工具的简单使用与常见问题
1、配置git 选择左上角目录file->setting 打开,Version Control 目录下Git,选择git安装目录下的git.exe文件; 点击test,出现git版本,则表示git识别成功,点击右下角确认即可生效。 2、配置node.js 选…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...
