c#: 表达式树的简化
环境:
- .net 6
一、问题?
有下面的表达式:
var nums = new List<int> { 1, 2, 3 };
Expression<Func<int, bool>> exp = i => i > nums.Max();
我们知道,它其实就是:exp = i => i > 3;
那么问题是,我们如何将它改造成这样呢?
在orm解析lambda生成sql时,也经常遇到这样的窘境:
var scores = new List<Person> { new Person { Id = 1, Score = 60 } };
var sql = orm.Select<Person>().Where(i => i.Score > scores.Select(i=>i.Score).Max() || i.Score == 100).ToSql();
//error:
// System.Exception:“未实现函数表达式 value(Program+<>c__DisplayClass0_0).scores.Select(i => i.Score).Max() 解析,如果正在操作导航属性集合,请使用 .AsSelect().Max()”public class Person
{public int Id { get; set; }public double Score { get; set; }
}
所以,就有了个想法:能不能对表达式进行简化呢?
就比如上面的可以改造成:orm.Select<Person>().Where(i => i.Score > 60 || i.Score == 100).ToSql();
二、表达式树简化原理
lambda表达式是表达式树的根, 它可能会有参数列表, 其子孙节点可能会引用这些参数, 也可能没有引用, 将没有引用的分支编译求值, 将结果再“放回”表达式中即可!
还是以下面的表达式为例:
var nums = new List<int> { 1, 2, 3 };
Expression<Func<int, bool>> exp = i => i > nums.Max();
在节点 > 的右侧 nums.Max() 没有引用参数列表, 那么它就可以被简化, 简化后就是:
exp = i => i > 3;
再看如下:
var nums = new List<int> { 1, 2, 3 };
Expression<Func<int, bool>> expr = i => i > nums.Max() || nums.Count > 0;
我们不仅可以将 || 右侧的简化为 true, 还可以根据||的短路特性对整体进行简化, 结果如下:
exp = i => true
三、表达式树的树状图
我们知道有各种各样的表达式类型, 如: +-/*,Call/MemberInit等。
无论哪种类型, 都可以将它们抽象成一棵树, 如:
Call类型的表达式, 可以看成:
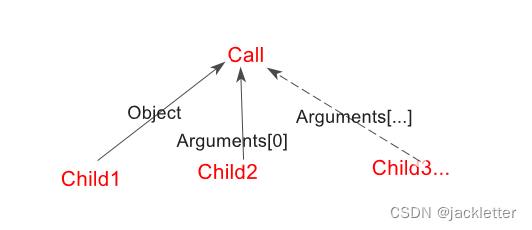
表达式的嵌套:
lambda表达式有可能会嵌套lambda, 如:
var nums = new List<int> { 1, 2, 3 };
Expression<Func<int>> expr = () => Filter(nums, i => i > 1);static int Filter(List<int> nums, Func<int, bool> func)
{return nums.First(i => func(i));
}
它的结构树如下:
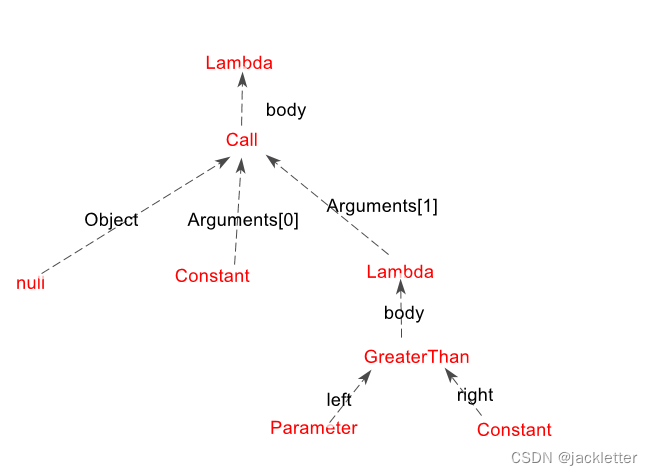
这个是函数接受委托的, 还有函数接受lambda的,如:
var nums = new List<int> { 1, 2, 3 };
Expression<Func<int>> expr = () => Filter(nums, i => i > 1);
static int Filter(List<int> nums, Expression<Func<int, bool>> expression)
{return nums.First(i => expression.Compile()(i));
}
此时,它的结构树如下:
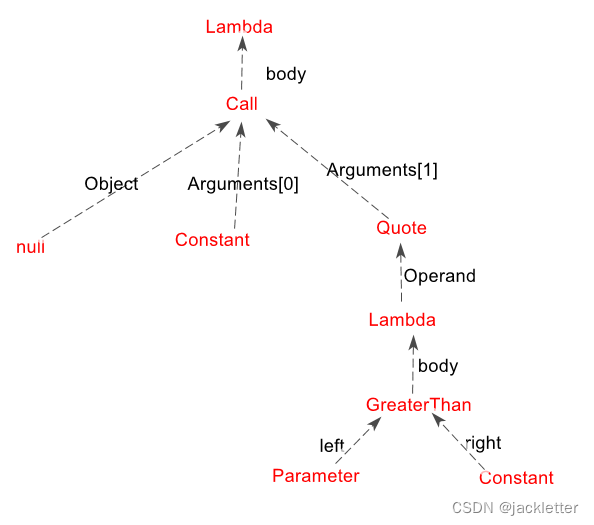
四、成品代码
在DotNetCommon.Core``已封装好了表达式树简化的方法,如下:

更多细节,参考:《DotNetCommon源码》
相关文章:

c#: 表达式树的简化
环境: .net 6 一、问题? 有下面的表达式: var nums new List<int> { 1, 2, 3 }; Expression<Func<int, bool>> exp i > i > nums.Max();我们知道,它其实就是:exp i > i > 3; 那么…...
13. UE5 RPG限制Attribute的值的范围以及生成结构体
前面几章,我们实现了通过GameplayEffect对Attribute值的修改,比如血量和蓝量,我们都是有一个最大血量和最大蓝量去限制它的最大值,而且血量和蓝量最小值不会小于零。之前我们是没有实现相关限制的,接下来,我…...

UE4运用C++和框架开发坦克大战教程笔记(十九)(第58~60集)完结
UE4运用C和框架开发坦克大战教程笔记(十九)(第58~60集)完结 58. 弹窗显示与隐藏59. UI 面板销毁60. 框架完成与总结 58. 弹窗显示与隐藏 这节课我们先来补全 TransferMask() 里对于 Overlay 布局类型面板的遮罩转移逻辑ÿ…...

ModuleNotFoundError: No module named ‘_ctypes‘报错解决方案
1、须命令安装libbffi-devel软件包: yum install libffi-devel -y2、安装完后再重装python3,无须卸载 找到之前的python3安装包,如果安装包删除了通过 history | grep python命令找到最初安装时的包下载的命令下载,保证版本一样&…...

【服务器数据恢复】服务器RAID模块硬件损坏的数据恢复案例
服务器数据恢复环境&故障: 某品牌服务器中有一组由数块SAS硬盘组建的RAID5磁盘阵列,服务器操作系统是WINDOWS SERVER,服务器中存放企业数据,无数据库文件。 服务器出故障之前出现过几次意外断电的情况,服务器断电…...

spring boot3x登录开发-上(整合jwt)
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 前置条件 jwt简介 导依赖 编写jwt工具类 1.配置项直接嵌入代码,通过类名.静态方法使用 2.配置项写到…...

git 克隆拉取代码出现私钥权限问题。
问题反馈: rootdd:~/android/boost-1.74-for-android-r20b# git clone https://github.com/liulilittle/boost-1.74-for-android-r20b.git Cloning into boost-1.74-for-android-r20b... WARNING: UNPROTECTED PRIVATE KEY FILE! Permissions 0777 for /root/…...
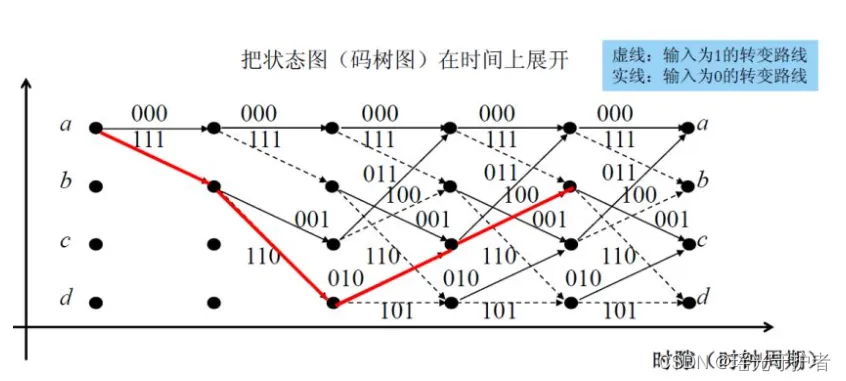
【5G NR】【一文读懂系列】移动通讯中使用的信道编解码技术-卷积码原理
目录 一、引言 二、卷积编码的发展历史 2.1 卷积码的起源 2.2 主要发展阶段 2.3 重要里程碑 三、卷积编码的基本概念 3.1 基本定义 3.2 编码器框图 3.3 编码多项式 3.4 网格图(Trellis)描述 四、MATLAB示例 一、引言 卷积编码,作为数字通信领域中的一项…...

揭开Markdown的秘籍:标题|文字样式|列表
🌈个人主页:聆风吟 🔥系列专栏:Markdown指南、网络奇遇记 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️Markdown 标题二. ⛳️Markdown 文字样式2.1 🔔斜体2.2 &…...

移动最小二乘法
移动最小二乘法(Moving Least Square,MLS)主要应用于曲线与曲面拟合,该方法基于紧支撑加权函数(即函数值只在有限大小的封闭域中定义大于零,而在域外则定义为零)和多项式基函数,通过…...

【LeetCode】37. 解数独(困难)——代码随想录算法训练营Day30
题目链接:37. 解数独 题目描述 编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&…...

VUE学习——属性绑定
属性绑定,就是给html添加id、class这样类似的操作。 <template><div v-bind:id"dynamicId"><div v-bind:class"dynamicClass">Test</div></div> </template><script>export default{data(){return{…...
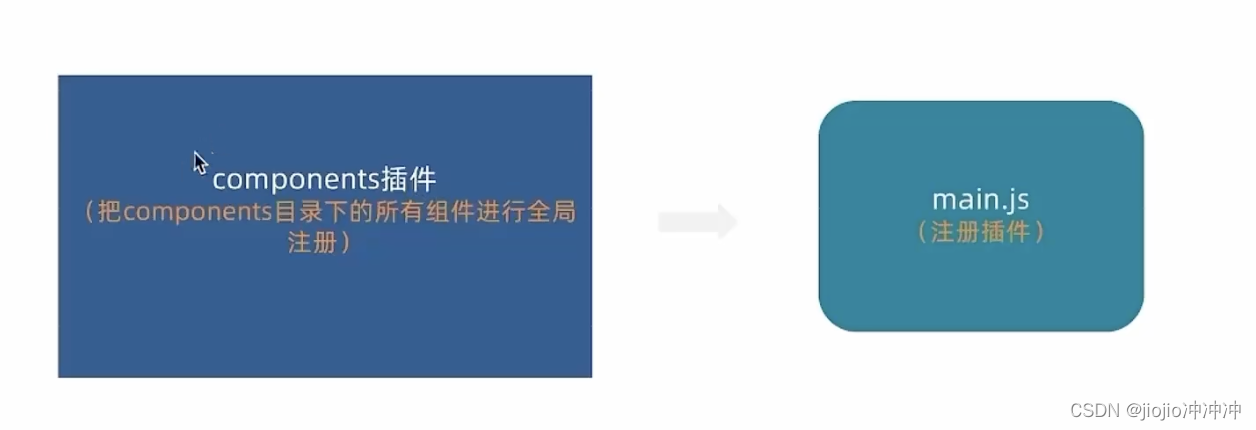
vue3 之 通用组件统一注册全局
components/index.js // 把components中的所组件都进行全局化注册 // 通过插件的方式 import ImageView from ./ImageView/index.vue import Sku from ./XtxSku/index.vue export const componentPlugin {install (app) {// app.component(组件名字,组件配置对象)…...
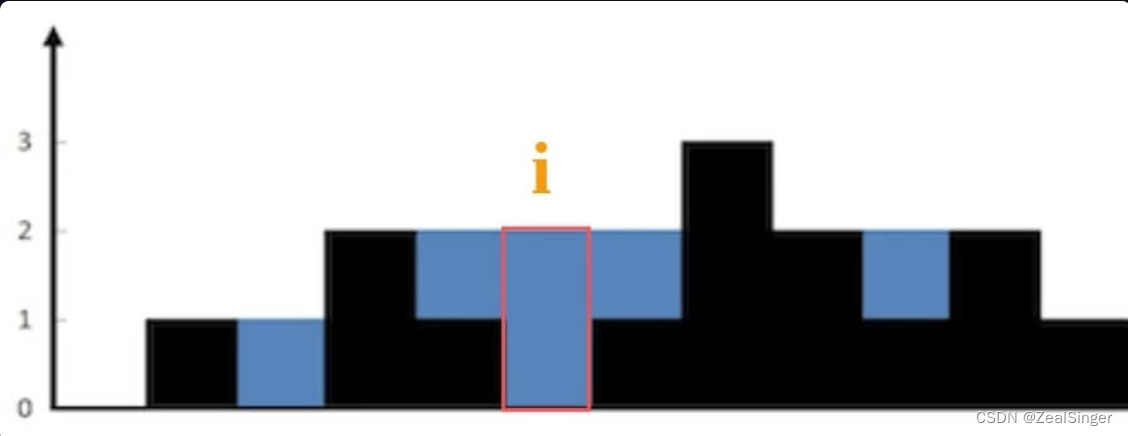
[Java][算法 双指针]Day 02---LeetCode 热题 100---04~07
LeetCode 热题 100---04~07 第一题:移动零 思路 找到每一个为0的元素 然后移到数组的最后 但是需要注意的是 要在给定的数组原地进行修改 并且其他非零元素的相对顺序不能改变 我们采用双指针法 定义两个指针i和j i和j一开始分别都在0索引位置 然后判断j所…...

【问题解决】如何将一个服务器的docker迁移到另一个服务器
要将Docker容器从一台机器迁移到另一台机器,可以按照以下步骤操作: 在机器A上提交容器为镜像: 使用docker commit命令将运行中的容器保存为新的镜像。这里需要容器的ID或名称,以及你想要命名的目标镜像名。 docker commit [容器…...

C++单例模式详解
目录 0. 前言 1. 懒汉式单例模式 1.1 最简单的单例模式 1.2 防止内存泄漏 1.2.1 智能指针的方法 1.2.2 静态嵌套的方法 1.3 保证线程安全 1.4 C11版本的优雅解决方案 2. 饿汉式单例模式 0. 前言 起因是在程序中重复声明了一个单例模式的变量,后来程序怎么调…...
LLM应用开发与落地:流式响应
一、背景 最近智能客服产品给到一个游戏客户那边,客户那边的客服负责人体验后认为我们产品回答的准确率是还是比较高的。同时,他反馈了几个需要改进的地方,其中一个就是机器人回复慢。机器人回复慢有很多原因,也有优化方式&#…...
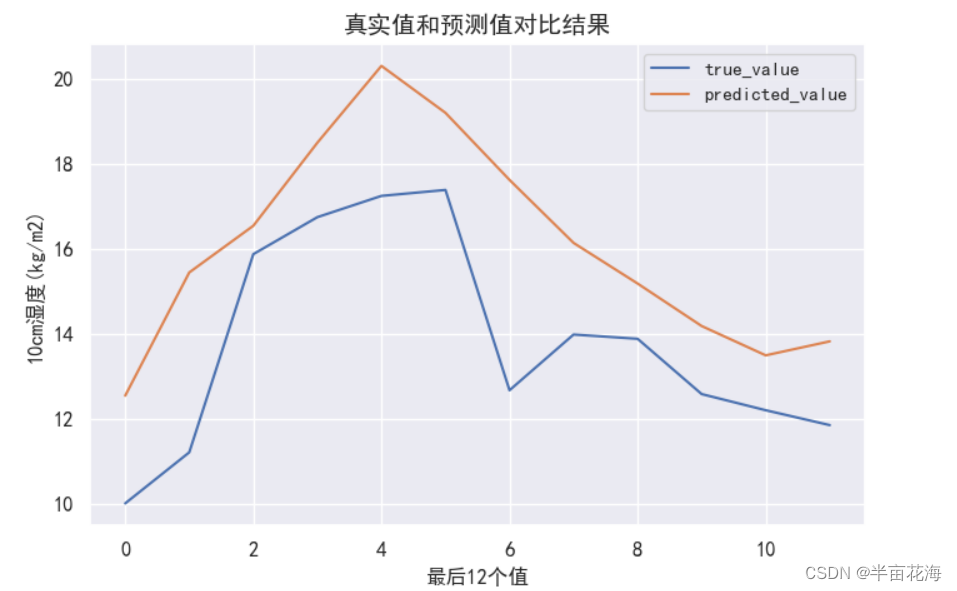
神经网络 | 基于 CNN 模型实现土壤湿度预测
Hi,大家好,我是半亩花海。在现代农业和环境监测中,了解土壤湿度的变化对于作物生长和水资源管理至关重要。通过深度学习技术,特别是卷积神经网络,我们可以利用过去的土壤湿度数据来预测未来的湿度趋势。本文将使用 Pad…...
江科大STM32 终
目录 SPI协议10.1 SPI简介W25Q64简介10.3 SPI软件读写W25Q6410.4 SPI硬件外设读写W25Q64 BKP备份寄存器、PER电源控制器、RTC实时时钟11.0 Unix时间戳代码示例:读写备份寄存器BKP11.2 RTC实时时钟 十二、PWR电源控制12.1 PWR简介代码示例:修改主频12.3 串…...

《MySQL 简易速速上手小册》第10章:未来趋势和进阶资源(2024 最新版)
文章目录 10.1 MySQL 在云计算和容器化中的应用10.1.1 基础知识10.1.2 重点案例:使用 Python 部署 MySQL 到 Kubernetes10.1.3 拓展案例 1:在 AWS RDS 上部署 MySQL 实例10.1.4 拓展案例 2:使用 Docker 部署 MySQL 10.2 MySQL 和 NoSQL 的整合…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
