第三十天| 51. N皇后
Leetcode 51. N皇后
题目链接:51 N皇后
题干:按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将
n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数
n,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中
'Q'和'.'分别代表了皇后和空位。
思考:回溯法。先定义结果集result,再考虑回溯函数:
| 参数 | 含义 |
| n | 题目给定皇后个数 |
| chessboard | 当前棋盘摆放情况 |
| row | 当前处理行数 |
终止条件:如果当前处理行数row等于n时说明皇后已全部摆放完毕,将当前棋盘摆放情况chessboard存放到结果集result中。
单层搜索逻辑:从下标0开始循环处理每个二维坐标位置,若当前行row当前列col存放皇后合法则摆放皇后,递归处理,最后回溯。
验证row行col列摆放皇后合法性:参数当前行列值,当前棋盘以及皇后个数。三处标准判断合法性:不能同行(每次处理都是不同行故此标准不用验证)、不能同列、不能同斜线 (45度和135度角)。
- 判断同列:当前row行前面的所以行对应的col列是否摆放过皇后
- 判断45°线:当前row行col列45°斜方向是否摆放过皇后
- 判断135°线:当前row行col列135°斜方向是否摆放过皇后
代码:
class Solution {
public:vector<vector<string>> result;//n : 皇后个数 chessboard : 当前棋盘摆放情况 row : 当前处理行数void backtracking(const int n, vector<string>& chessboard, int row) {if (row == n) {result.push_back(chessboard);return;}for (int col = 0; col < n; col++) {if (isValid(n, chessboard, row, col)) {chessboard[row][col] = 'Q'; //摆放皇后backtracking(n, chessboard, row + 1);chessboard[row][col] = '.'; //回溯}}}//判断row行col列摆放皇后是否合法bool isValid(const int n, vector<string>& chessboard, int row, int col) {//检查此行是否摆放过皇后for (int i = 0; i < row; i++) if (chessboard[i][col] == 'Q')return false;//检查45°线是否摆放过皇后for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) if (chessboard[i][j] == 'Q')return false;//检查135°线是否摆放过皇后for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++)if (chessboard[i][j] == 'Q')return false;return true;}vector<vector<string>> solveNQueens(int n) {result.clear();vector<string> chessboard(n, string(n, '.'));backtracking(n, chessboard, 0);return result;}
};回溯法专题总结:
- 熟悉回溯法代码整体框架。把回溯问题抽象为树形结构,其搜索的过程:for循环横向遍历,递归纵向遍历,回溯不断调整结果集。
- 确定是否使用startIndex。对于组合问题,如果是一个集合来求组合的话,就需要startIndex;如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex。
- 熟悉同层去重两种方式。排序后相邻元素比较以及set容器记录使用情况。了解到节点去重,但未归纳。
- 明确在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果。
相关文章:

第三十天| 51. N皇后
Leetcode 51. N皇后 题目链接:51 N皇后 题干:按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整…...
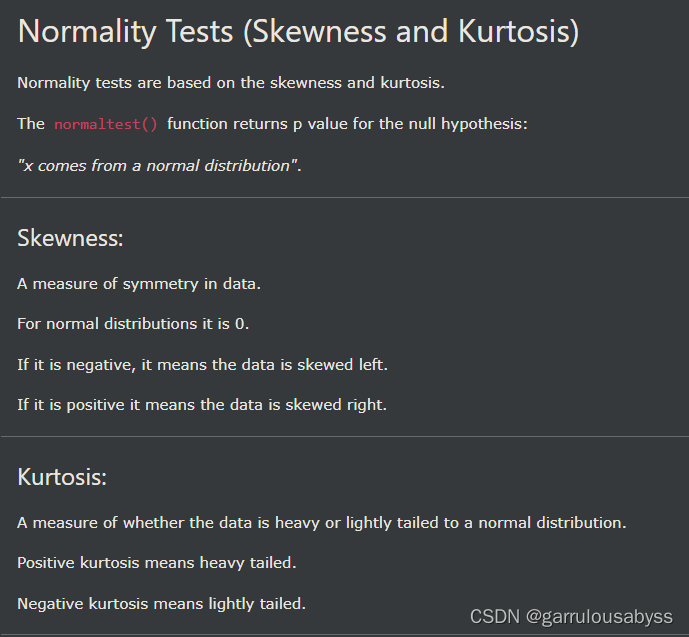
pythn-scipy 查漏补缺
1. 2. 3. 4. 5. 6. 7. 8. 9. 偏度 skewness,峰度 kurtosis...

【JavaScript 漫游】【013】Date 对象知识点摘录
文章简介 本文为【JavaScript 漫游】专栏的第 013 篇文章,记录了 JS 语言中 Date 对象的重要知识点。 普通函数的用法构造函数的用法日期的运算静态方法,包括:Date.now()、Date.parse() 和 Date.UTC()实例方法,包括:…...

vue.config.js和webpack.config.js区别
webpack.config.js和vue.config.js的区别 webpack.config.js是webpack的配置文件,所有使用webpack作为打包工具的项目都可以使用,vue的项目可以使用,react的项目也可以使用。 vue.config.js是vue项目的配置文件,专用于vue项目。…...

H12-821_73
73.某台路由器Router LSA如图所示,下列说法中错误的是? A.本路由器的Router ID为10.0.12.1 B.本路由器为DR C.本路由器已建立邻接关系 D.本路由器支持外部路由引入 答案:B 注释: LSA中的链路信息Link ID,Data…...
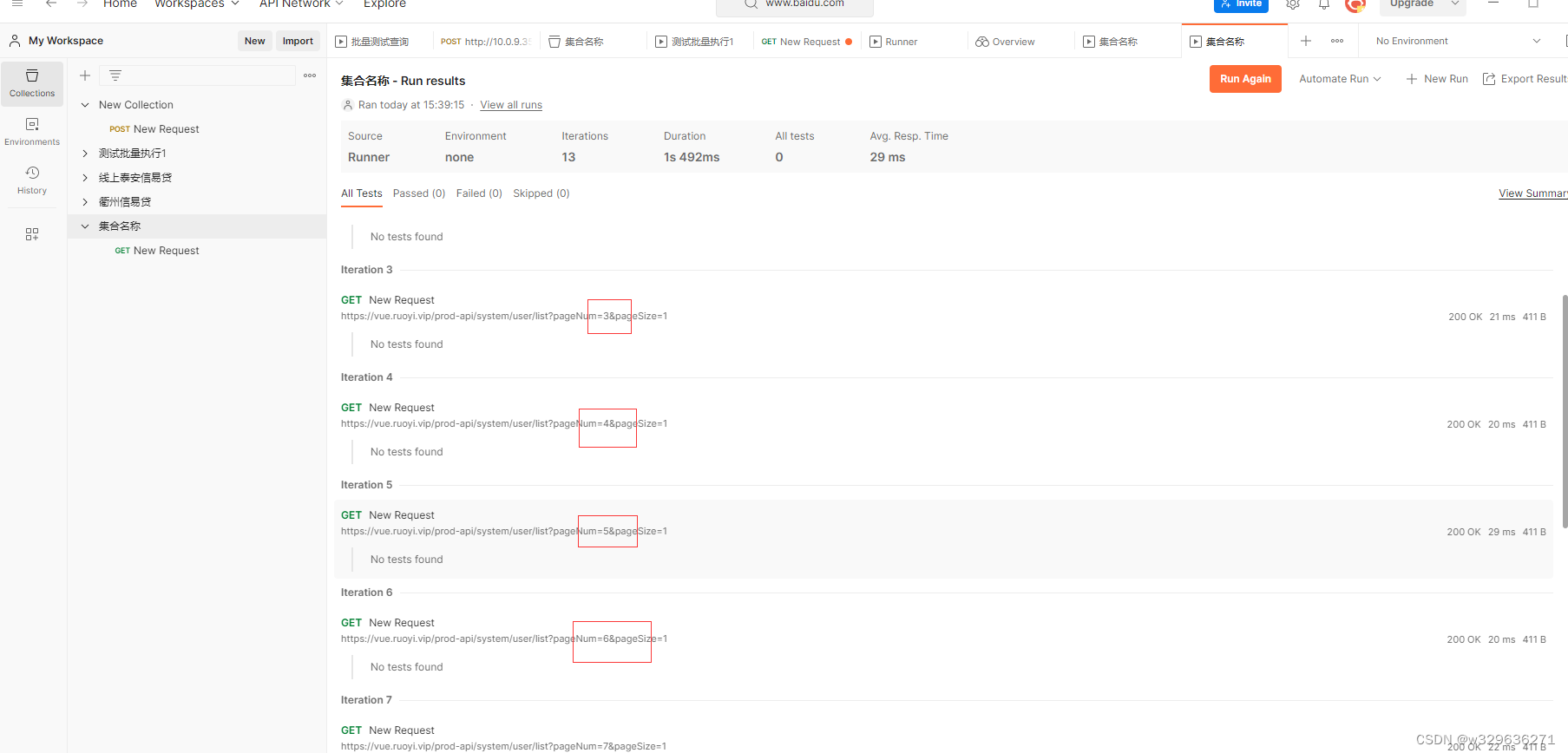
postman执行批量测试
1.背景 有许多的人常常需要使用第三方系统进行重复的数据查询,本文介绍使用PostMan的方式对数据进行批量的查询,减少重复的劳动。 2.工具下载 3.初入门 一、如图示进行点击,创建collection 二、输入对应的名称 三、创建Request并进行查…...

蓝桥杯基础知识8 list
蓝桥杯基础知识8 list 01 list 的定义和结构 lits使用频率较低,是一种双向链表容器,是标准模板库(STL)提供的一种序列容器,lsit容器以节点(node)的形式存储元素,使用指针将这些节点链…...
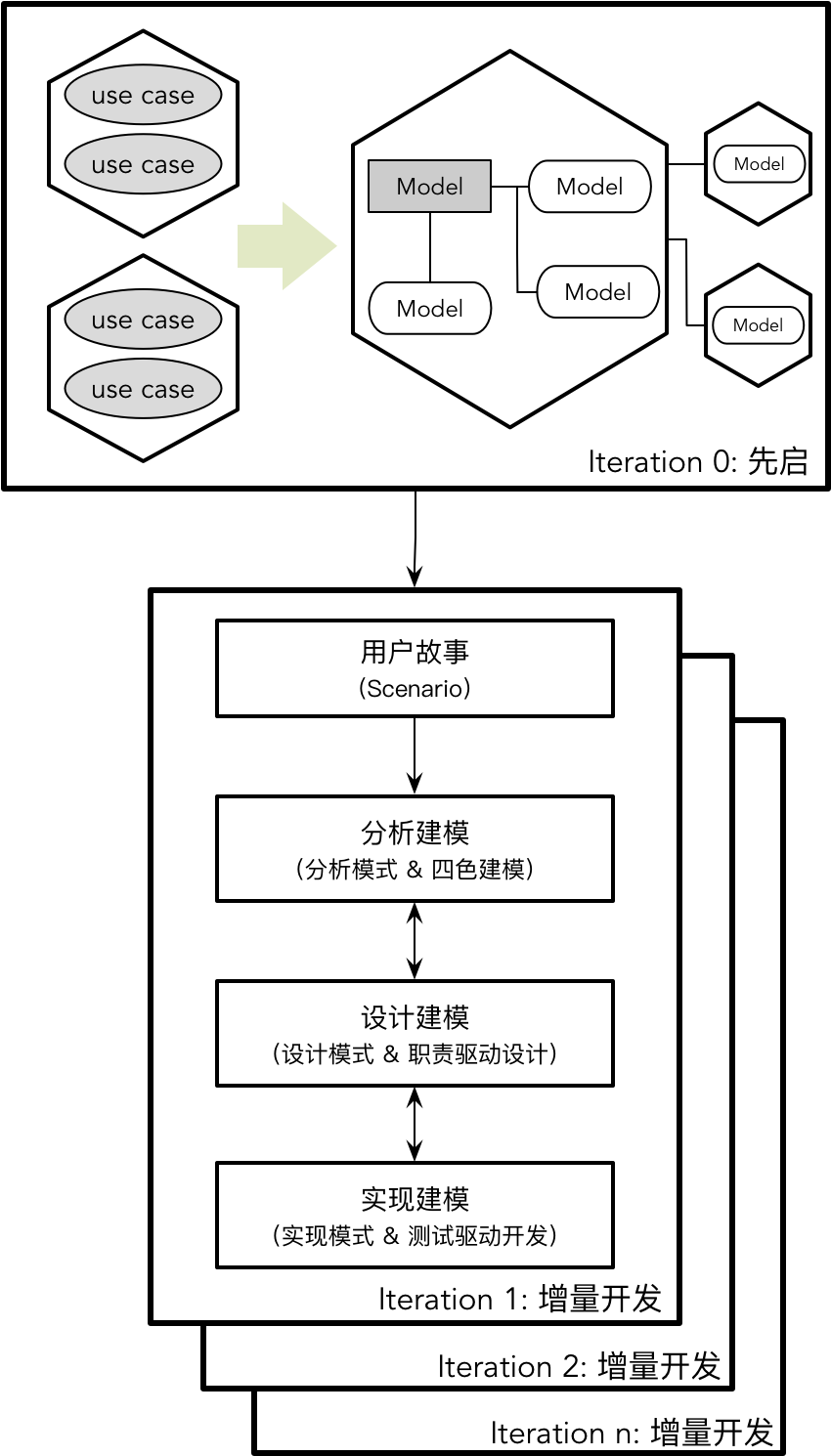
【DDD】学习笔记-理解领域模型
Eric Evans 的领域驱动设计是对软件设计领域的一次重新审视,是在面向对象语言大行其道时对数据建模的“拨乱反正”。Eric 强调了模型的重要性,例如他在书中总结了模型在领域驱动设计中的作用包括: 模型和设计的核心互相影响模型是团队所有成…...

v-if 和v-show 的区别
第074个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 提供vue2的一些基本操作:安装、引用,模板使用,computed&a…...

LabVIEW网络测控系统
LabVIEW网络测控系统 介绍了基于LabVIEW的网络测控系统的开发与应用,通过网络技术实现了远程的数据采集、监控和控制。系统采用LabVIEW软件与网络通信技术相结合,提高了系统的灵活性和扩展性,适用于各种工业和科研领域的远程测控需求。 随着…...

攻防世界 CTF Web方向 引导模式-难度1 —— 11-20题 wp精讲
PHP2 题目描述: 暂无 根据dirsearch的结果,只有index.php存在,里面也什么都没有 index.phps存在源码泄露,访问index.phps 由获取的代码可知,需要url解码(urldecode )后验证id为admin则通过 网页工具不能直接对字母进行url编码 …...

华为Eth-Trunk级联堆叠接入IPTV网络部署案例
Eth-Trunk级联堆叠接入IPTV网络部署案例 组网图形 图2 Eth-Trunk级联堆叠IPTV基本组网图 方案简介配置注意事项组网需求数据规划配置思路操作步骤配置文件 方案简介 随着IPTV业务的迅速发展,IPTV平台承载的用户也越来越多,用户对IPTV直播业务的可靠性…...
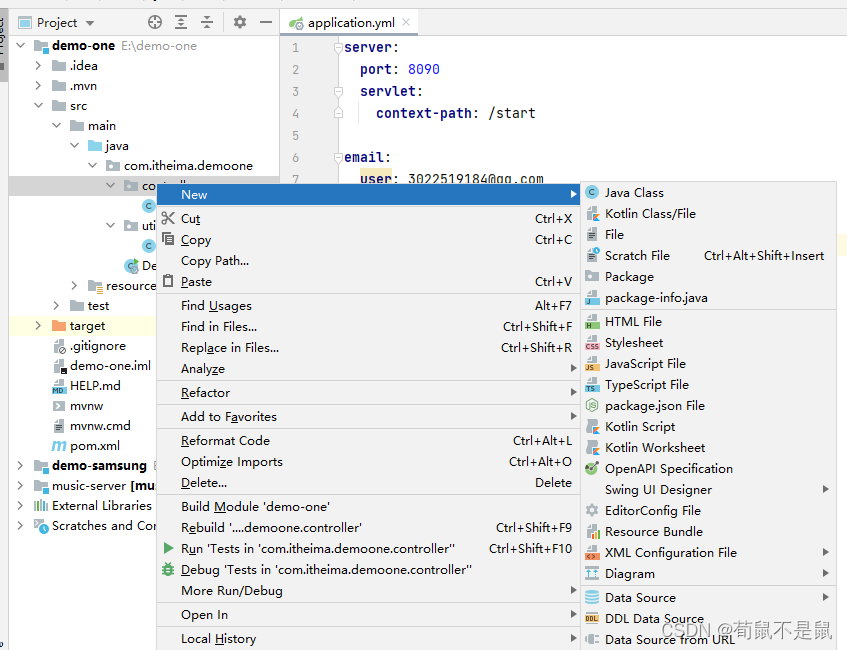
idea: 无法创建Java Class文件(SpringBoot)已解决
第一:点击file-->project Sructure... 第二步:点击Moudules 选择自己需要创建java的文件夹(我这里选择的是main)右键点击Sources,然后点击OK即可 然后就可以创建java类了...

ChinaXiv:中科院科技论文预发布平台
文章目录 Main彩蛋 Main 主页:https://chinaxiv.org/home.htm 彩蛋...
)
【人工智能】Fine-tuning 微调:解析深度学习中的利器(7)
在深度学习领域,Fine-tuning 微调是一项重要而强大的技术,它为我们提供了在特定任务上充分利用预训练模型的途径。本文将深入讨论 Fine-tuning 的定义、原理、实际操作以及其在不同场景中的应用,最后简要探讨Fine-tuning 的整体架构。 1. Fi…...
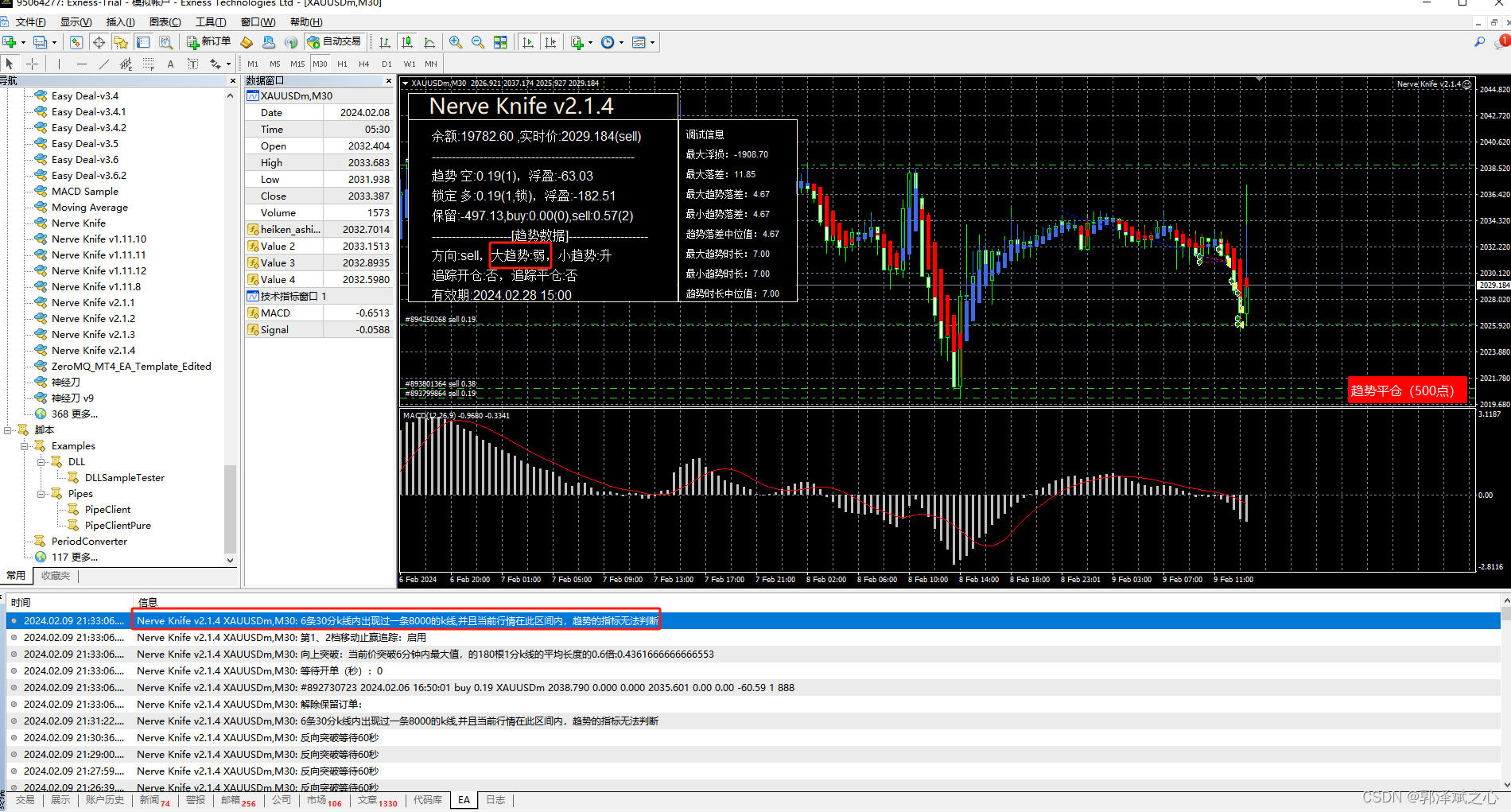
黄金交易策略(Nerve Nnife):大K线对技术指标的影响
我们使用heiken ashi smoothed来做敏感指标(大趋势借助其转向趋势预判,但不是马上转变),has默认使用6根k线的移动平均值来做计算的。若在6根k线规范内有一个突变的行情(k线很长),那么整个行情的…...

django中实现数据迁移
在Django中,数据迁移(data migrations)通常指的是将模型(models)中的数据从一个状态迁移到另一个状态。这可以涉及很多操作,比如添加新字段、删除字段、更新字段的数据类型,或者更改表之间的关系…...
全新抖音快手小红书去水印系统网站源码 | 支持几十种平台
全新抖音快手小红书去水印系统网站源码 | 支持几十种平台...

ChatGPT炸裂了
优质内容:ChatGPT太炸裂了 hello,我是小索奇 很多人在使用ChatGPT时遇到了两个主要问题,导致他们觉得这个工具并没有带来太多实际价值。首先,许多人发现ChatGPT的回答缺乏深度,缺乏实用性。其次,一些人在使…...

小白代码审计入门
最近小白一直在学习代码审计,对于我这个没有代码审计的菜鸟来说确实是一件无比艰难的事情。但是着恰恰应了一句老话:万事开头难。但是小白我会坚持下去。何况现在已经喜欢上了代码审计,下面呢小白就说一下appcms后台模板Getshell以及读取任意文件,影响的版本是2.0.101版本。…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
