备战蓝桥杯---动态规划之经典背包问题
看题:
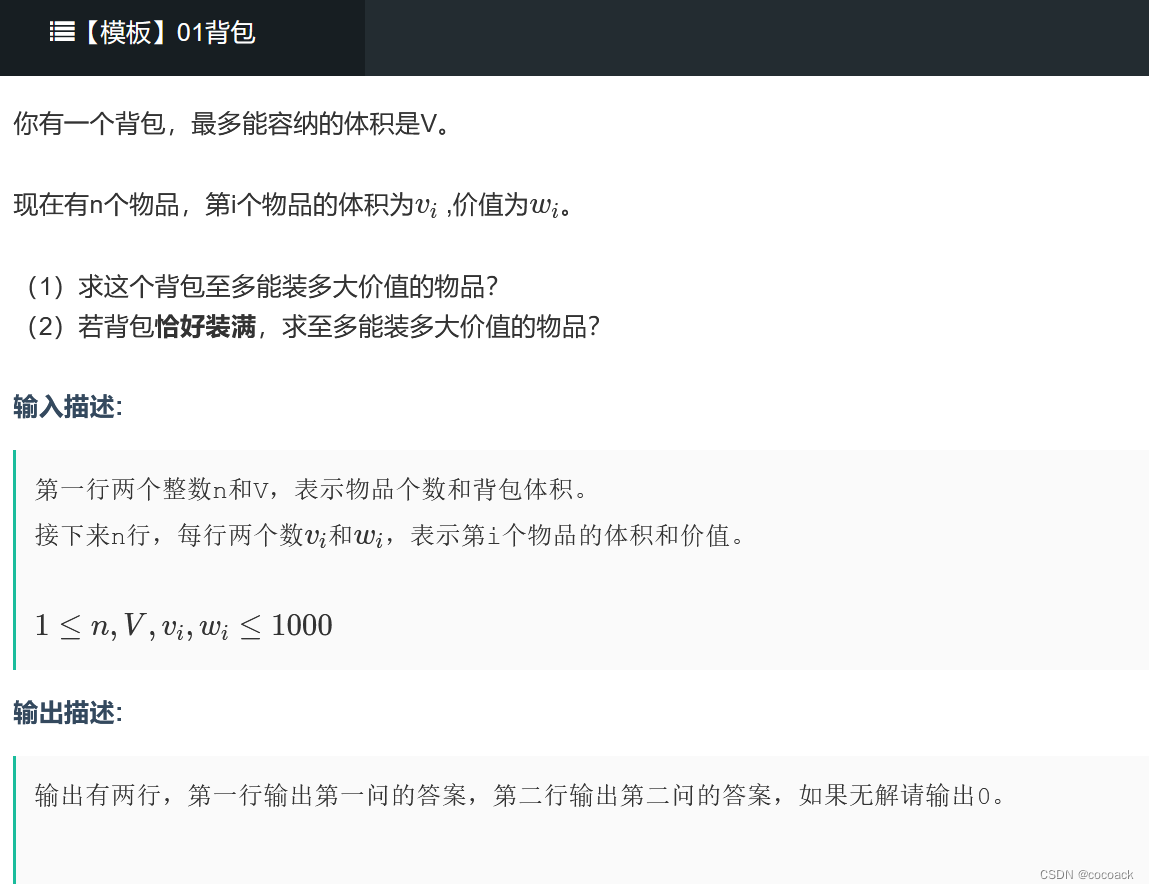
我们令f[i][j]为前i个物品放满容量为j的背包的最大价值。
f[i][j]=max(f[i-1][j],f[i-1][j-c[i]]+w[i]);
我们开始全副成负无穷。f[0][0]=0;最后循环最后一行求max;
负无穷:0xc0c0c0c0;正无穷:0x3f3f3f3f
下面是v=12,n=6的图示:

下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,v1,v[1002],w[1002],dp[1002][1002];
signed main(){cin>>n>>v1;for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);memset(dp,-0x3f,sizeof(dp));dp[0][0]=0;for(int i=1;i<=n;i++){for(int j=0;j<=v1;j++){if(j>=v[i]) dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);else dp[i][j]=dp[i-1][j];}}int ans=0;for(int i=0;i<=v1;i++){ans=max(ans,dp[n][i]);}cout<<ans<<endl;if(dp[n][v1]<=0) cout<<0;else cout<<dp[n][v1];
}事实上,我们可以想象一些有体积但是没有价值的空气,显然,他不会影响最后的结果,而且它保证了对于每一行它的值递增,因此我们for循环可以省去。(不过这个前提是题目保证不一定要塞满)
加点难度:
n<=20,v<=10^9;N小,我们直接DFS
n<=100,v<=10^9:
我们可以用map来存每一行的值,对于负无穷,我们直接忽略,对于那先体积比小的大但是价值比他们小的也舍弃。
下面是代码:
#include<bits/stdc++.h>
using namespace std;
int n,v[1005],v1,w[1005],q;
map<int,int> ck[2];
int main(){cin>>n>>v1;for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);ck[0][0]=0;map<int,int>::iterator it;map<int,int>::iterator it1;for(int i=1;i<=n;i++){it=ck[(i-1)%2].begin();it1=ck[(i-1)%2].begin();while((it1->first)<v[i]&&it1!=ck[(i-1)%2].end()){ck[i%2][it1->first]=it1->second;it1++;}q=(--it1)->second;while(it!=ck[(i-1)%2].end()){if(it->first+v[i]>v1) break;if(ck[(i-1)%2].count(it->first+v[i])!=0){ck[i%2][it->first+v[i]]=max(ck[(i-1)%2][it->first]+w[i],ck[(i-1)%2][it->first+v[i]]);}else ck[i%2][it->first+v[i]]=ck[(i-1)%2][it->first]+w[i];if(q<ck[i%2][it->first+v[i]]) q=ck[i%2][it->first+v[i]];else{ck[i%2].erase(it->first+v[i]);}it++;}ck[(i-1)%2].clear();}cout<<(--ck[n%2].end())->second<<endl;
}接下来我们看一下完全背包:

很容易,我们可得:f[i][j]=max(f[i-1][j-k*c[i]]+k*w[i])(0<=k*c[i]<=j)
其中,复杂度为k*n*v;
f[i][j]=max(f[i-1][j],f[i-1][j-c]+w,f[i-1][j-2*c]+2*w,.........)
f[i][j-c]=max(f[i-1][j-c],f[i-1][j-2*c]+w,......)
于是,f[i][j]=max(f[i][j-c]+w,f[i-1][j])
这样,我们就把复杂度->n*v;
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,v1,v[1005],w[1005],dp[1005];
int main(){cin>>n>>v1;memset(dp,0xc0c0c0c0,sizeof(dp));for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);dp[0]=0;for(int i=1;i<=n;i++){for(int j=v[i];j<=v1;j++){dp[j]=max(dp[j],dp[j-v[i]]+w[i]);}}int ans=0;for(int i=0;i<=v1;i++) ans=max(ans,dp[i]);cout<<ans<<endl;if(dp[v1]<0) cout<<0;else cout<<dp[v1];
}看看多重背包:
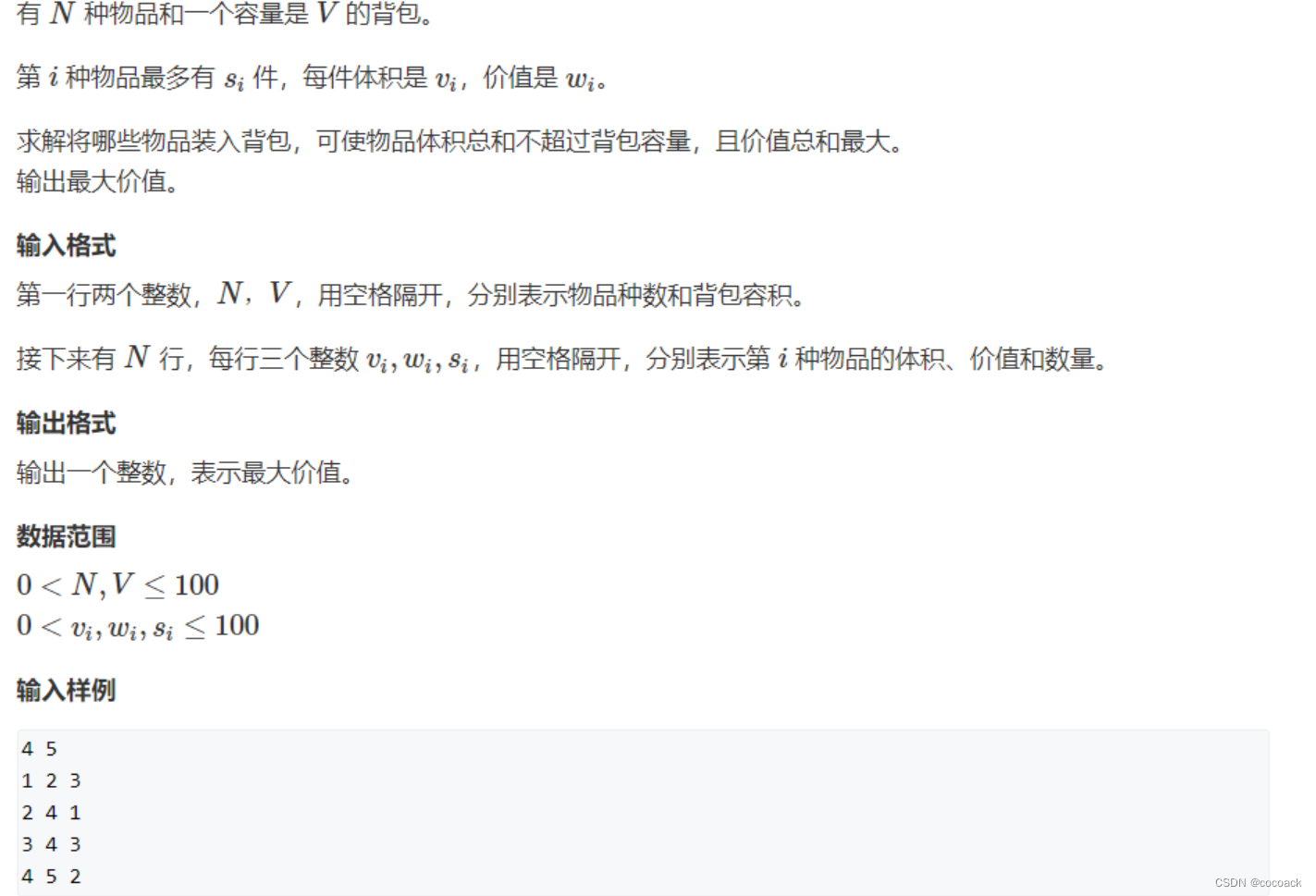
我们可以吧一样的背包看成不一样的,这样就转化为求0/1背包,但是这样的复杂度还是和上一题类似。
我们考虑优化一下:
假如有7个物品,我们如何用跟小的数字表示它所有的方案?
我们可以采用二进制的思想--》1,2,4包,每一个方案可以组合成所有可能。
我们把数分成1,2,4,8....加上剩余的数即可。
下面是二进制压缩代码:
for(int i=1;i<=n;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);int k=1;while(k<c){v[cnt]=k*a;w[cnt++]=k*b;c-=k;k*=2;}if(c){v[cnt]=c*a;w[cnt]=c*b;}}相关文章:

备战蓝桥杯---动态规划之经典背包问题
看题: 我们令f[i][j]为前i个物品放满容量为j的背包的最大价值。 f[i][j]max(f[i-1][j],f[i-1][j-c[i]]w[i]); 我们开始全副成负无穷。f[0][0]0;最后循环最后一行求max; 负无穷:0xc0c0c0c0;正无穷:0x3f3f3f3f 下面是v12,n6的图示ÿ…...
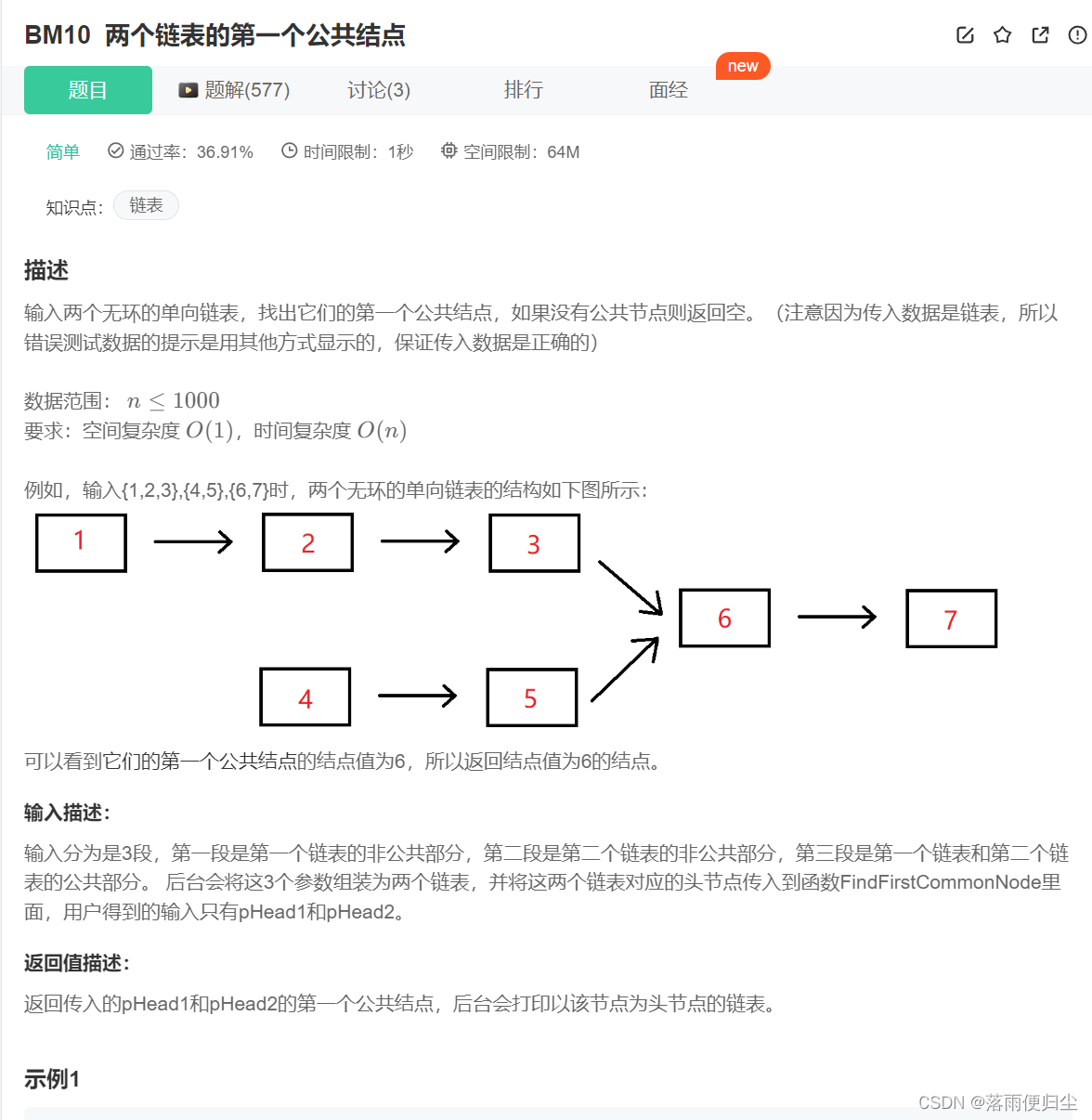
Go语言每日一练——链表篇(八)
传送门 牛客面试笔试必刷101题 ----------------两个链表的第一个公共结点 题目以及解析 题目 解题代码及解析 解析 这一道题使用的还是双指针算法,我们先求出两个链表的长度差n,然后定义快慢指针,让快指针先走n步,最后快慢指…...
跟着cherno手搓游戏引擎【23】项目维护、2D引擎之前的一些准备
项目维护: 修改文件结构: 头文件自己改改就好了 创建2DRendererLayer: Sandbox2D.h: #pragma once #include "YOTO.h" class Sandbox2D :public YOTO::Layer {public:Sandbox2D();virtual ~Sandbox2D() default;virtual void O…...
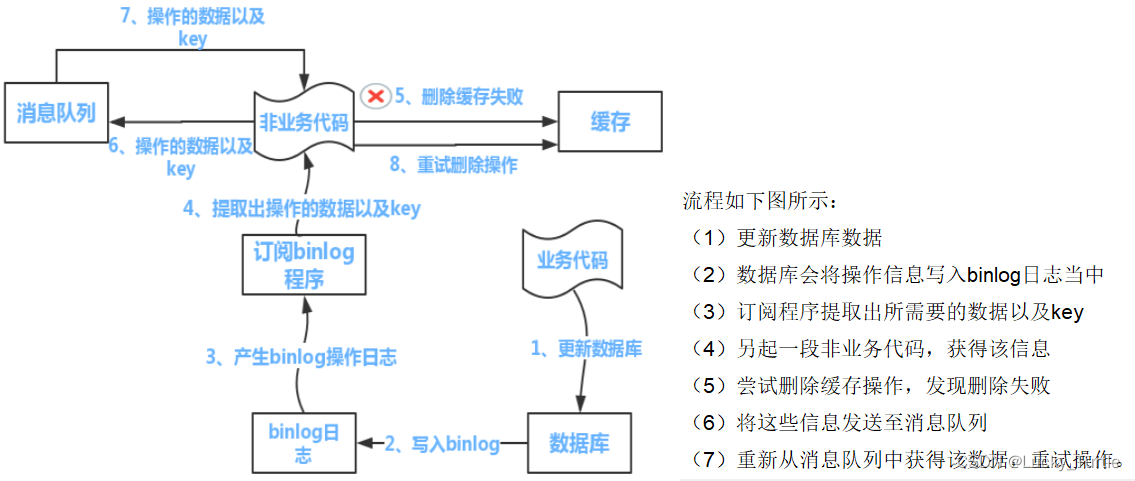
Redis(十三)缓存双写一致性策略
文章目录 概述示例 缓存双写一致性缓存按照操作来分,细分2种读写缓存:同步直写策略读写缓存:异步缓写策略双检加锁策略 数据库和缓存一致性更新策略先更新数据库,再更新缓存先更新缓存,再更新数据库先删除缓存…...

7 scala的类构造器
在创建对象的时候,需要调用类的构造器。Scala 提供了主构造器和辅助构造器。 1 主构造器 与 Java 一样,如果我们没有特别定义,那么 Scala 提供的默认构造器是没有参数的。 我们可以在类名后,指定构造器的参数列表,列…...
如何在 Mac 上恢复永久删除的文件:有效方法
您是否错误地从 Mac 中删除了某个文件,并且确信它已经永远消失了?好吧,你可能错了。即使您认为已永久删除计算机上的数据,仍有可能将其恢复。 在本文中,您将了解如何在 Mac 上恢复永久删除的文件,并了解增…...

Web后端开发:事务与AOP
事务管理 在学习数据库时,讲到:事务是一组操作的集合,它是一个不可分割的工作单位。事务会把所有的操作作为一个整体,一起向数据库提交或者是撤销操作请求,要么同时成功,要么同时失败。 事务的操作主要有三…...
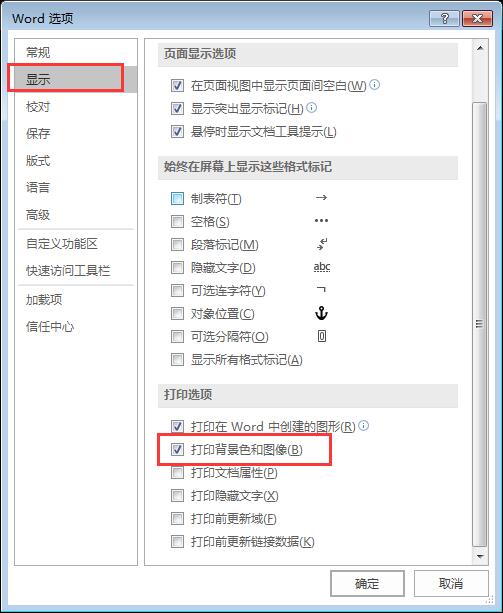
[word] word如何打印背景和图片? #微信#其他#经验分享
word如何打印背景和图片? 日常办公中会经常要打印文件的,其实在文档的打印中也是有很多技巧的,可以按照自己的需求设定,下面给大家分享word如何打印背景和图片,一起来看看吧! 1、打印背景和图片 在默认的…...
Maven - 编译报错:程序包 XXX 不存在(多模块项目)
问题描述 编译报错:程序包 XXX 不存在(多模块项目) 原因分析 检查依赖模块 pom 文件,看是不是引入了如下插件 <plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-pl…...

Vue事件中如何使用 event 对象
在Vue中,事件处理函数常常需要获取事件触发时的相关信息,比如鼠标位置、按键信息等。而要获取这些信息,就需要使用event对象。那么在Vue的事件中如何正确使用event对象呢?接下来就来详细介绍一下。 首先,在Vue的事件中…...
Golang GC 介绍
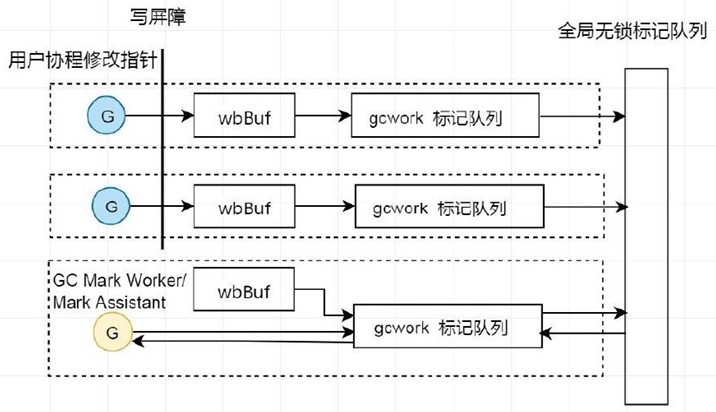
文章目录 0.前言1.发展史2.并发三色标记清除和混合写屏障2.1 三色标记2.2 并发标记问题2.3 屏障机制Dijkstra 插入写屏障Yuasa 删除写屏障混合写屏障 3.GC 过程4.GC 触发时机5.哪里记录了对象的三色状态?6.如何观察 GC?方式1:GODEBUGgctrace1…...

决策树之scikit-learn
实例 from sklearn.datasets import load_iris from sklearn import tree import matplotlib.pyplot as plt# Load iris dataset iris load_iris() X, y iris.data, iris.target# Fit the classifier clf tree.DecisionTreeClassifier() clf clf.fit(X, y)# Plot the deci…...

Python爬虫之关系型数据库存储#5
关系型数据库是基于关系模型的数据库,而关系模型是通过二维表来保存的,所以它的存储方式就是行列组成的表,每一列是一个字段,每一行是一条记录。表可以看作某个实体的集合,而实体之间存在联系,这就需要表与…...

ANSI Escape Sequence 下落的方块
ANSI Escape Sequence 下落的方块 1. ANSI Escape 的用途 无意中发现 B站有人讲解, 完全基于终端实现俄罗斯方块。 基本想法是借助于 ANSI Escape Sequence 实现方方块的绘制、 下落动态效果等。对于只了解 ansi escape sequence 用于 log 的颜色打印的人来说&…...
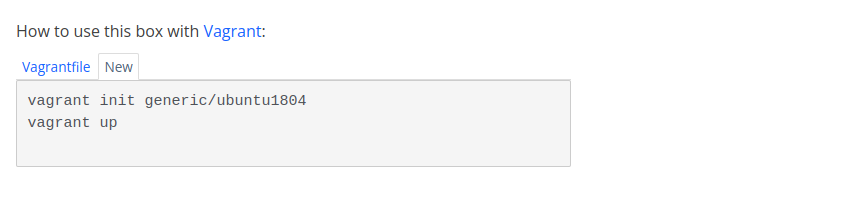
Vagrant 虚拟机工具基本操作指南
Vagrant 虚拟机工具基本操作指南 #虚拟机 # #vargant# #ubuntu# 虚拟机virtualbox ,VMWare及WSL等大家都很了解了,那Vagrant是什么东西? 它是一组命令行工具,可以象Docker管理容器一样管理虚拟机,这样快速创…...

中年低端中产程序员从西安出发到海南三亚低成本吃喝万里行:西安-南宁-湛江-雷州-徐闻-博鳌-陵水-三亚-重庆-西安
文章大纲 旅途规划来回行程的确定南宁 - 北海 - 湛江轮渡成为了最终最大的不确定性!感谢神州租车气温与游玩地点总体花费 游玩过程出发时间:Day1-1月25日星期四,西安飞南宁路途中:Day2-1月26日星期五,南宁-湛江-住雷州…...

企业级Spring boot项目 配置清单
目录 一、服务基础配置 二、配置数据库数据源 三、配置缓存 四、配置日志 五、配置统一异常处理 六、配置swagger文档 七、配置用户登录模块 八、配置websocket 九、配置定时任务 十、配置文件服务器 十一、配置Nacos 十二、配置项目启动数据库默认初始化(liquibas…...
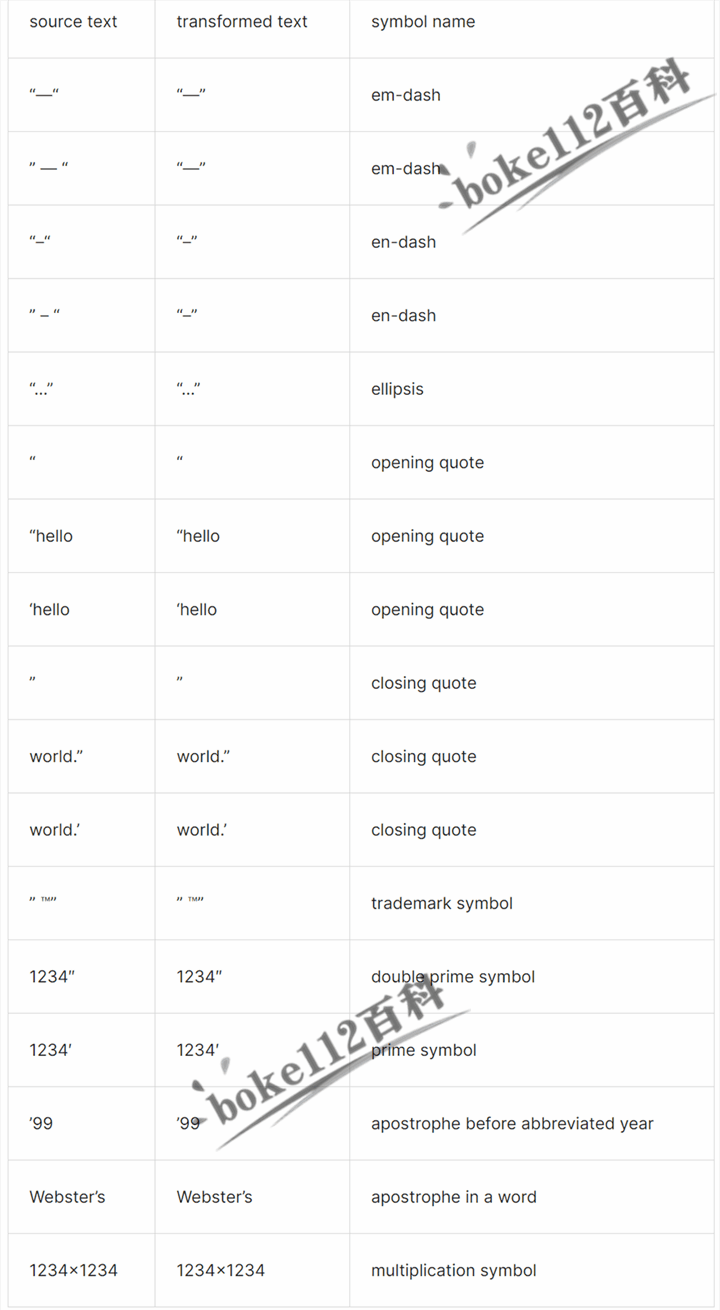
WordPress函数wptexturize的介绍及用法示例,字符串替换为HTML实体
在查看WordPress你好多莉插件时发现代码中使用了wptexturize()函数用来随机输出一句歌词,下面boke112百科就跟大家一起来学习一下WordPress函数wptexturize的介绍及用法示例。 WordPress函数wptexturize介绍 wptexturize( string $text, bool $reset false ): st…...

【Iceberg学习三】Reporting和Partitioning原理
Metrics Reporting Type of Reports 从 1.1.0 版本开始,Iceberg 支持 MetricsReporter 和 MetricsReport API。这两个 API 允许表达不同的度量报告,并支持一种可插拔的方式来报告这些报告。 ScanReport(扫描报告) 扫描报告&am…...
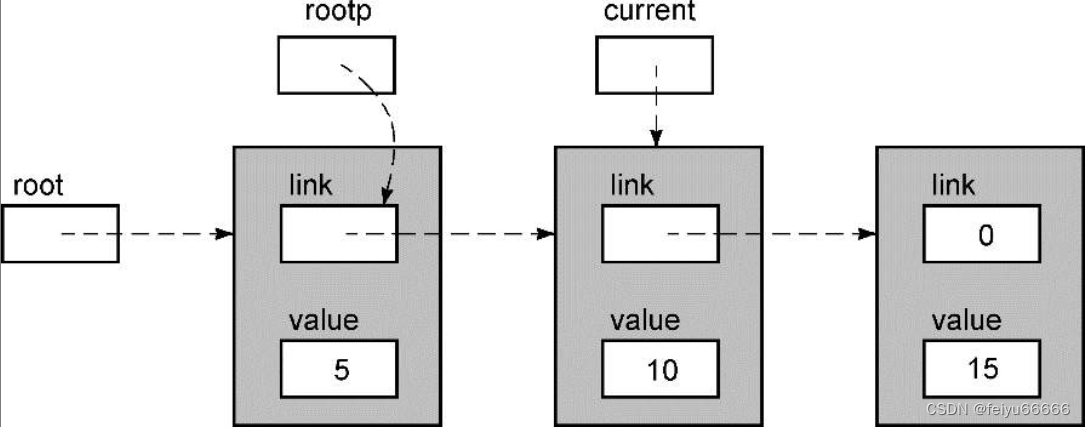
肯尼斯·里科《C和指针》第12章 使用结构和指针(1)链表
只恨当时学的时候没有读到这本书,,,,,, 12.1 链表 有些读者可能还不熟悉链表,这里对它作一简单介绍。链表(linked list)就一些包含数据的独立数据结构(通常称为节点)的集…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
