【机器学习】单变量线性回归
文章目录
- 线性回归模型(linear regression model)
- 损失/代价函数(cost function)——均方误差(mean squared error)
- 梯度下降算法(gradient descent algorithm)
- 参数(parameter)和超参数(hyperparameter)
- 代码实现样例
- 运行结果
源代码文件请点击此处!
线性回归模型(linear regression model)
- 线性回归模型:
f w , b ( x ) = w x + b f_{w,b}(x) = wx + b fw,b(x)=wx+b
其中, w w w 为权重(weight), b b b 为偏置(bias)
- 预测值(通常加一个帽子符号):
y ^ ( i ) = f w , b ( x ( i ) ) = w x ( i ) + b \hat{y}^{(i)} = f_{w,b}(x^{(i)}) = wx^{(i)} + b y^(i)=fw,b(x(i))=wx(i)+b
损失/代价函数(cost function)——均方误差(mean squared error)
- 一个训练样本: ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i))
- 训练样本总数 = m m m
- 损失/代价函数是一个二次函数,在图像上是一个开口向上的抛物线的形状。
J ( w , b ) = 1 2 m ∑ i = 1 m [ f w , b ( x ( i ) ) − y ( i ) ] 2 = 1 2 m ∑ i = 1 m [ w x ( i ) + b − y ( i ) ] 2 \begin{aligned} J(w, b) &= \frac{1}{2m} \sum^{m}_{i=1} [f_{w,b}(x^{(i)}) - y^{(i)}]^2 \\ &= \frac{1}{2m} \sum^{m}_{i=1} [wx^{(i)} + b - y^{(i)}]^2 \end{aligned} J(w,b)=2m1i=1∑m[fw,b(x(i))−y(i)]2=2m1i=1∑m[wx(i)+b−y(i)]2
- 为什么需要乘以 1/2?因为对平方项求偏导后会出现系数 2,是为了约去这个系数。
梯度下降算法(gradient descent algorithm)
- α \alpha α:学习率(learning rate),用于控制梯度下降时的步长,以抵达损失函数的最小值处。若 α \alpha α 太小,梯度下降太慢;若 α \alpha α 太大,下降过程可能无法收敛。
- 梯度下降算法:
r e p e a t { t m p _ w = w − α ∂ J ( w , b ) w t m p _ b = b − α ∂ J ( w , b ) b w = t m p _ w b = t m p _ b } u n t i l c o n v e r g e \begin{aligned} repeat \{ \\ & tmp\_w = w - \alpha \frac{\partial J(w, b)}{w} \\ & tmp\_b = b - \alpha \frac{\partial J(w, b)}{b} \\ & w = tmp\_w \\ & b = tmp\_b \\ \} until \ & converge \end{aligned} repeat{}until tmp_w=w−αw∂J(w,b)tmp_b=b−αb∂J(w,b)w=tmp_wb=tmp_bconverge
其中,偏导数为
∂ J ( w , b ) w = 1 m ∑ i = 1 m [ f w , b ( x ( i ) ) − y ( i ) ] x ( i ) ∂ J ( w , b ) b = 1 m ∑ i = 1 m [ f w , b ( x ( i ) ) − y ( i ) ] \begin{aligned} & \frac{\partial J(w, b)}{w} = \frac{1}{m} \sum^{m}_{i=1} [f_{w,b}(x^{(i)}) - y^{(i)}] x^{(i)} \\ & \frac{\partial J(w, b)}{b} = \frac{1}{m} \sum^{m}_{i=1} [f_{w,b}(x^{(i)}) - y^{(i)}] \end{aligned} w∂J(w,b)=m1i=1∑m[fw,b(x(i))−y(i)]x(i)b∂J(w,b)=m1i=1∑m[fw,b(x(i))−y(i)]
参数(parameter)和超参数(hyperparameter)
- 超参数(hyperparameter):训练之前人为设置的任何数量都是超参数,例如学习率 α \alpha α
- 参数(parameter):模型在训练过程中创建或修改的任何数量都是参数,例如 w , b w, b w,b
代码实现样例
import numpy as np
import matplotlib.pyplot as plt# 计算误差均方函数 J(w,b)
def cost_function(x, y, w, b):m = x.shape[0] # 训练集的数据样本数cost_sum = 0.0for i in range(m):f_wb = w * x[i] + bcost = (f_wb - y[i]) ** 2cost_sum += costreturn cost_sum / (2 * m)# 计算梯度值 dJ/dw, dJ/db
def compute_gradient(x, y, w, b):m = x.shape[0] # 训练集的数据样本数d_w = 0.0d_b = 0.0for i in range(m):f_wb = w * x[i] + bd_wi = (f_wb - y[i]) * x[i]d_bi = (f_wb - y[i])d_w += d_wid_b += d_bidj_dw = d_w / mdj_db = d_b / mreturn dj_dw, dj_db# 梯度下降算法
def linear_regression(x, y, w, b, learning_rate=0.01, epochs=1000):J_history = [] # 记录每次迭代产生的误差值for epoch in range(epochs):dj_dw, dj_db = compute_gradient(x, y, w, b)# w 和 b 需同步更新w = w - learning_rate * dj_dwb = b - learning_rate * dj_dbJ_history.append(cost_function(x, y, w, b)) # 记录每次迭代产生的误差值return w, b, J_history# 绘制线性方程的图像
def draw_line(w, b, xmin, xmax, title):x = np.linspace(xmin, xmax)y = w * x + b# plt.axis([0, 10, 0, 50]) # xmin, xmax, ymin, ymaxplt.xlabel("X-axis", size=15)plt.ylabel("Y-axis", size=15)plt.title(title, size=20)plt.plot(x, y)# 绘制散点图
def draw_scatter(x, y, title):plt.xlabel("X-axis", size=15)plt.ylabel("Y-axis", size=15)plt.title(title, size=20)plt.scatter(x, y)# 从这里开始执行
if __name__ == '__main__':# 训练集样本x_train = np.array([1, 2, 3, 5, 6, 7])y_train = np.array([15.5, 19.7, 24.4, 35.6, 40.7, 44.8])w = 0.0 # 权重b = 0.0 # 偏置epochs = 10000 # 迭代次数learning_rate = 0.01 # 学习率J_history = [] # # 记录每次迭代产生的误差值w, b, J_history = linear_regression(x_train, y_train, w, b, learning_rate, epochs)print(f"result: w = {w:0.4f}, b = {b:0.4f}") # 打印结果# 绘制迭代计算得到的线性回归方程plt.figure(1)draw_line(w, b, 0, 10, "Linear Regression")plt.scatter(x_train, y_train) # 将训练数据集也表示在图中plt.show()# 绘制误差值的散点图plt.figure(2)x_axis = list(range(0, 10000))draw_scatter(x_axis, J_history, "Cost Function in Every Epoch")plt.show()运行结果


相关文章:

【机器学习】单变量线性回归
文章目录 线性回归模型(linear regression model)损失/代价函数(cost function)——均方误差(mean squared error)梯度下降算法(gradient descent algorithm)参数(parame…...

《计算思维导论》笔记:10.4 关系模型-关系运算
《大学计算机—计算思维导论》(战德臣 哈尔滨工业大学) 《10.4 关系模型-关系运算》 一、引言 本章介绍数据库的基本数据模型:关系模型-关系运算。 二、什么是关系运算 在数据库理论中,关系运算(Relational Operatio…...
)
QT+OSG/osgEarth编译之八十四:osgdb_osg+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_osg)
文章目录 一、osgdb_osg介绍二、文件分析三、pro文件四、编译实践一、osgdb_osg介绍 osgDB是OpenSceneGraph(OSG)库中的一个模块,用于加载和保存3D场景数据。osgDB_osg是osgDB模块中的一个插件,它提供了对OSG格式的支持。 OSG格式是OpenSceneGraph库使用的一种二进制文件…...

【Redis快速入门】初识Redis、Redis安装、图形化界面
个人名片: 🐼作者简介:一名大三在校生,喜欢AI编程🎋 🐻❄️个人主页🥇:落798. 🐼个人WeChat:hmmwx53 🕊️系列专栏:🖼️…...
Linux(Ubuntu) 环境搭建:Nginx
注:服务器默认以root用户登录 NGINX 官方网站地址:https://nginx.org/en/NGINX 官方安装文档地址:https://nginx.org/en/docs/install.html服务器的终端中输入以下指令: # 安装 Nginx apt-get install nginx # 查看版本信息 ngi…...

快速手动完成 VS 编写脚本自动化:如何选取最高效的工作方式?
那些不懂技术的朋友们可能会觉得,写代码写脚本不就是敲敲键盘嘛,搞那么高科技做什么,直接手工点点鼠标不就完事了。 这种看法很常见,但实际情况要复杂得多。 首先,手工操作虽然对于短期和小规模的任务来说似乎更快&am…...

FAST角点检测算法
FAST(Features from Accelerated Segment Test)角点检测算法是一种快速且高效的角点检测方法。它通过检测每个像素周围的连续像素集合,确定是否为角点。以下是 FAST 角点检测算法的基本流程: FAST 角点检测算法的基本过程主要包括…...
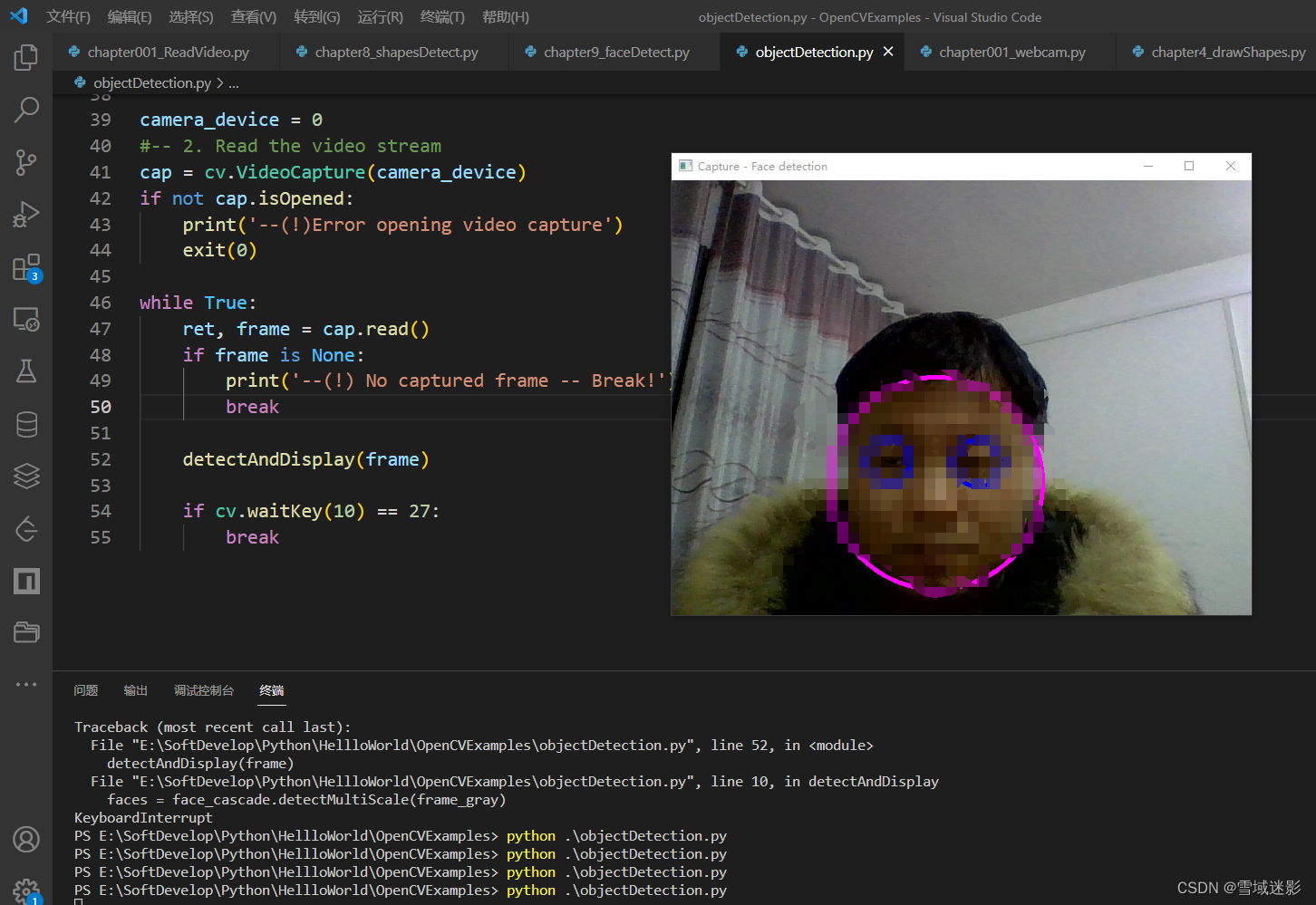
Python中使用opencv-python进行人脸检测
Python中使用opencv-python进行人脸检测 之前写过一篇VC中使用OpenCV进行人脸检测的博客。以数字图像处理中经常使用的lena图像为例,如下图所示: 使用OpenCV进行人脸检测十分简单,OpenCV官网给了一个Python人脸检测的示例程序,…...

牛客网 DP3跳台阶扩展问题
在原始跳台阶问题上,我们知道只走1,2阶台阶的话,可以推出来斐波那契数列的形式进行计算操作。但是,在这里就是1,2,3,...n阶台阶了。其实思路是一样的。 在原始台阶问题,我们的状态方…...

ARM汇编[1] 打印格式化字符串(printf
文章目录 写在前面关键知识简单加减乘除函数调用和循环系统调用栈的使用 GDB调试示例代码 写在前面 如果您对ARM汇编还一无所知的话请先参考ARM汇编hello world 本篇不会广泛详细的列举各种指令,仍然只讲解最关键的部分,然后使用他们来完成一个汇编程序…...
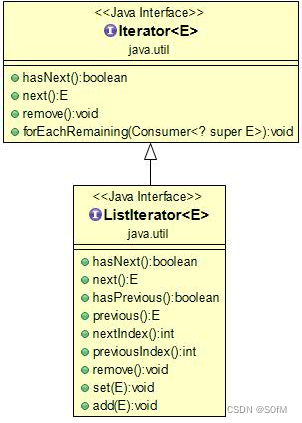
Java 集合、迭代器
Java 集合框架主要包括两种类型的容器,一种是集合(Collection),存储一个元素集合,另一种是图(Map),存储键/值对映射。Collection 接口又有 3 种子类型,List、Set 和 Queu…...
在 Docker 中启动 ROS2 里的 rivz2 和 rqt 出现错误的解决方法
1. 出现错误: 运行 ros2 run rivz2 rivz2 ,报错如下 : No protocol specified qt.qpa.xcb: could not connect to display :1 qt.qpa.plugin: Could not load the Qt platform plugin "xcb" in "" even though it was f…...
使用securecrt+xming通过x11访问ubuntu可视化程序
windows使用securecrtxming通过x11访问ubuntu可视化程序 windows机器IP:192.168.9.133 ubuntu-desktop20.04机器IP:192.168.9.190 windows下载xming并安装 按照图修改xming配置 开始->xming->Xlaunch 完成xming会在右下角后台运行 windows在…...
红队打靶练习:HEALTHCARE: 1
目录 信息收集 1、arp 2、nmap 3、nikto 4、whatweb 目录探测 1、gobuster 2、dirsearch WEB web信息收集 gobuster cms sqlmap 爆库 爆表 爆列 爆字段 FTP 提权 信息收集 本地提权 信息收集 1、arp ┌──(root㉿ru)-[~/kali] └─# arp-scan -l Inte…...

Java IO:概念和分类总结
前言 大家好,我是chowley,刚看完Java IO方面内容,特此总结一下。 Java IO Java IO(输入输出)是Java编程中用于处理输入和输出的API。它提供了一套丰富的类和方法,用于读取和写入数据到不同的设备、文件和…...
)
【Linux】基本命令(下)
目录 head指令 && tail指令 head指令 tail指令 find指令 grep指令 zip/unzip指令 tar指令 时间相关的指令 date显示 1.在显示方面,使用者可以设定欲显示的格式,格式设定为一个加号后接数个标记,其中常用的标记列表如下&…...

腾讯云游戏联机服务器配置价格表,4核16G/8核32G/4核32G/16核64G
2024年更新腾讯云游戏联机服务器配置价格表,可用于搭建幻兽帕鲁、雾锁王国等游戏服务器,游戏服务器配置可选4核16G12M、8核32G22M、4核32G10M、16核64G35M、4核16G14M等配置,可以选择轻量应用服务器和云服务器CVM内存型MA3或标准型SA2实例&am…...
面试经典150题——长度最小的子数组
"In the midst of winter, I found there was, within me, an invincible summer." - Albert Camus 1. 题目描述 2. 题目分析与解析 首先理解题意,题目要求我们找到一个长度最小的 连续子数组 满足他们的和大于target,需要返回的是子数组的…...

业务流程
一、需求分析和设计: 在项目启动阶段,需要与业务人员和产品经理充分沟通,了解业务需求,并根据需求进行系统设计和数据库设计。这一阶段的输出通常是需求文档、系统架构设计、数据库设计等。 1.需求文档 需求文档是一份非常重要…...
ChatGPT Plus如何升级?信用卡付款失败怎么办?如何使用信用卡升级 ChatGPT Plus?
ChatGPT Plus是OpenAI提供的一种高级服务,它相较于标准版本,提供了更快的响应速度、更强大的功能,并且用户可以优先体验到新推出的功能。 尽管许多用户愿意支付 20 美元的月费来订阅 GPT-4,但在实际支付过程中,特别是…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
