react函数组件中使用context
效果

1.在父组件中创建一个createcontext并将他导出
import React, { createContext } from 'react'
import Bpp from './Bpp'
import Cpp from './Cpp'
export let MyContext = createContext('我是组件B')
export let Ccontext = createContext('我是组件C')export default function App() {let a = '我是A组件传递的数据'let a1 = '我是A组件传递的二号数据'return (<MyContext.Provider value={a}><Ccontext.Provider value={a1}><div><div>context组件传值</div><div><Bpp /><Cpp /></div></div></Ccontext.Provider></MyContext.Provider>)
}2.子组件先将父组件引入,然后通过usecontext方法进行接收
import React, { useContext } from 'react'
import {Ccontext} from './App'export default function Cpp() {let Cdate=useContext(Ccontext)return (<div>{Cdate}</div>)
}相关文章:

react函数组件中使用context
效果 1.在父组件中创建一个createcontext并将他导出 import React, { createContext } from react import Bpp from ./Bpp import Cpp from ./Cpp export let MyContext createContext(我是组件B) export let Ccontext createContext(我是组件C)export default function App…...
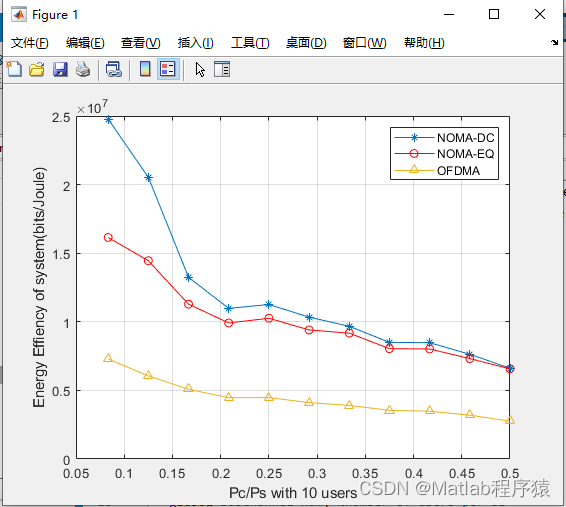
【MATLAB源码-第137期】基于matlab的NOMA系统和OFDMA系统对比仿真。
操作环境: MATLAB 2022a 1、算法描述 NOMA(非正交多址)和OFDMA(正交频分多址)是两种流行的无线通信技术,广泛应用于现代移动通信系统中,如4G、5G和未来的6G网络。它们的设计目标是提高频谱效…...

【FPGA Verilog】各种加法器Verilog
1bit半加器adder设计实例 module adder(cout,sum,a,b); output cout; output sum; input a,b; wire cout,sum; assign {cout,sum}ab; endmodule 解释说明 (1)assign {cout,sum}ab 是连续性赋值 对于线网wire进行赋值,必须以assign或者dea…...
)
【MySQL】-21 MySQL综合-7(MySQL主键+MySQL外检约束+MySQL唯一约束+MySQL检查约束)
MySQL主键MySQL外检约束MySQL唯一约束MySQL检查约束 MySQL主键选取设置主键约束的字段在创建表时设置主键约束在创建表时设置复合主键在修改表时添加主键约束 MySQL外键约束选取设置 MySQL 外键约束的字段在创建表时设置外键约束在修改表时添加外键约束删除外键约束 MySQL唯一约…...
【大厂AI课学习笔记】【1.6 人工智能基础知识】(3)神经网络
深度学习是机器学习中一种基于对数据进行表征学习的算法。观测值(例如一幅草莓照片)可以使用 多种方式来表示,如每个像素强度值的向量,或者更抽象地表示成一系列边、特定形状的区域等。 深度学习的最主要特征是使用神经网络作为计算模型。神经网络模型 …...
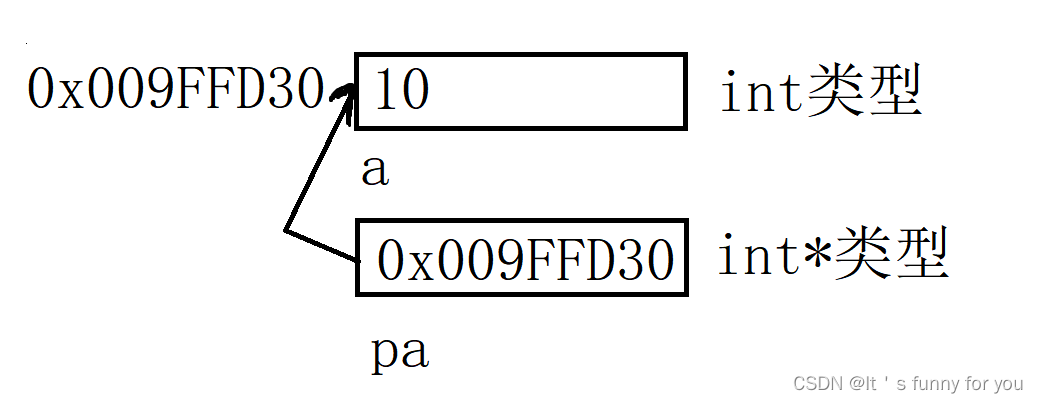
指针的基本含义及其用法
1.前言 在学习C语言的时候,我们会经常接触一个概念,指针和地址,关于这两个概念很多人并不能理解地十分透彻,接下来我将详细介绍一下这两者的概念 2.地址 我们知道计算机的上CPU(中央处理器)在处理数据的时…...

黄金交易策略(Nerve Nnife.mql4):趋势做单
完整EA:Nerve Knife.ex4黄金交易策略_黄金趋势ea-CSDN博客 当大小趋势相同行情走向也相同,就会开仓做顺势单,并会顺势追单,以达到快速止盈平仓的效果。大趋势追求稳定,小趋势追求敏捷,行情走向比小趋势更敏…...
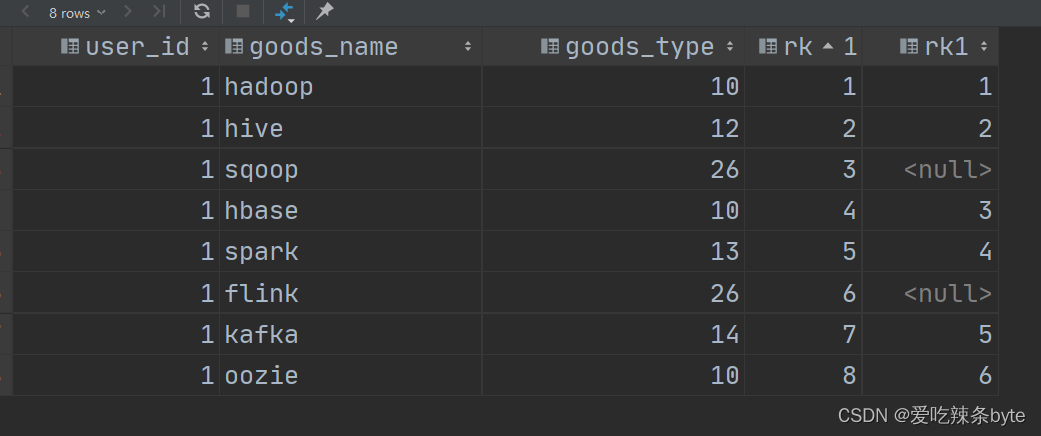
HiveSQL——条件判断语句嵌套windows子句的应用
注:参考文章: SQL条件判断语句嵌套window子句的应用【易错点】--HiveSql面试题25_sql剁成嵌套判断-CSDN博客文章浏览阅读920次,点赞4次,收藏4次。0 需求分析需求:表如下user_idgood_namegoods_typerk1hadoop1011hive1…...

ClickHouse--01--简介
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1. ClickHouse 简介官网: [https://clickhouse.com/docs/zh](https://clickhouse.com/docs/zh) 1.1 大数据处理场景1.2 什么是 ClickHouse1.3 OLAP 场景…...

【Django-ninja】在django ninja中处理异常
1. 直接抛内置异常 Django ninja内置了一些常用异常类。 from ninja.errors import HttpErrorapi.get("/some/resource") def some_operation(request):if True:raise HttpError(503, "Service Unavailable. Please retry later.")2. 覆写异常类 可以覆…...
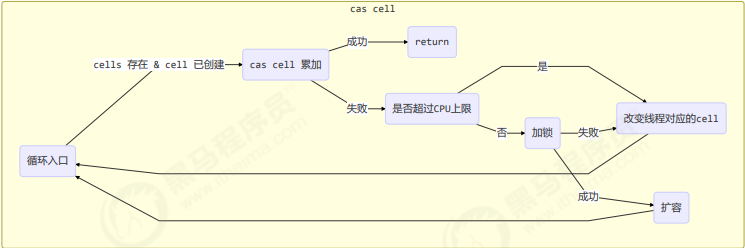
【并发编程】原子累加器
📝个人主页:五敷有你 🔥系列专栏:并发编程 ⛺️稳重求进,晒太阳 JDK8之后有专门做累加的类,效率比自己做快数倍以上 累加器性能比较 参数是方法 // supplier 提供者 无中生有 ()->结果// func…...
Java 基于微信小程序的电子商城购物系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12W、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

Git Push -f 命令详解
直接看原文: Git Push -f 命令详解 - 玩转Linux - SegmentFault 思否 -------------------------------------------------------------------------------------------------------------------------------- git push -f 这个命令的作用是将自己本地仓库的代码直接推送至仓…...

【LeetCode每日一题】前缀和的例题1248. 统计「优美子数组」974. 和可被 K 整除的子数组
leetcode 724. 寻找数组的中心索引 题目描述 给定一个整数类型的数组 nums,请编写一个能够返回数组 “中心索引” 的方法。 我们是这样定义数组 中心索引 的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。 如果数组不存在中心索引&…...

备战蓝桥杯---数学基础3
本专题主要围绕同余来讲: 下面介绍一下基本概念与定理: 下面给出解这方程的一个例子: 下面是用代码实现扩展欧几里得算法: #include<bits/stdc.h> using namespace std; int gcd(int a,int b,int &x,int &y){if(b…...

[算法学习] 逆元与欧拉降幂
费马小定理 两个条件: p为质数a与p互质 逆元 如果要求 x^-1 mod p ,用快速幂求 qmi(x,p-2) 就好 欧拉函数 思路:找到因数 i,phi / i * (i-1),除干净,判断最后的n 欧拉降幂 欧拉定理 应用示例 m! 是一个…...
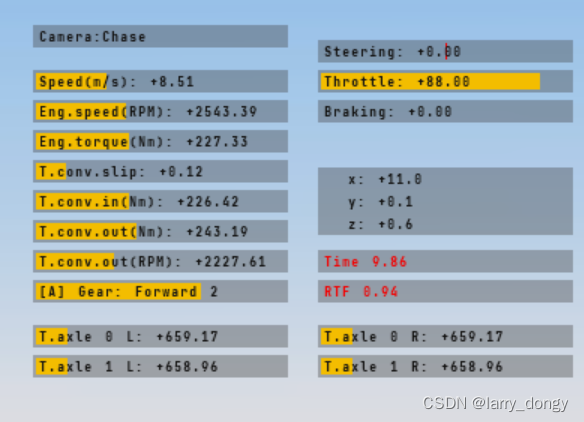
【Chrono Engine学习总结】4-vehicle-4.1-vehicle的基本概念
由于Chrono的官方教程在一些细节方面解释的并不清楚,自己做了一些尝试,做学习总结。 1、基本介绍 Vehicle Overview Vehicle Mannel Vehicle的官方demo 1.1 Vehicle的构型 一个车辆由许多子系统构成:悬挂、转向、轮子/履带、刹车/油门、动…...
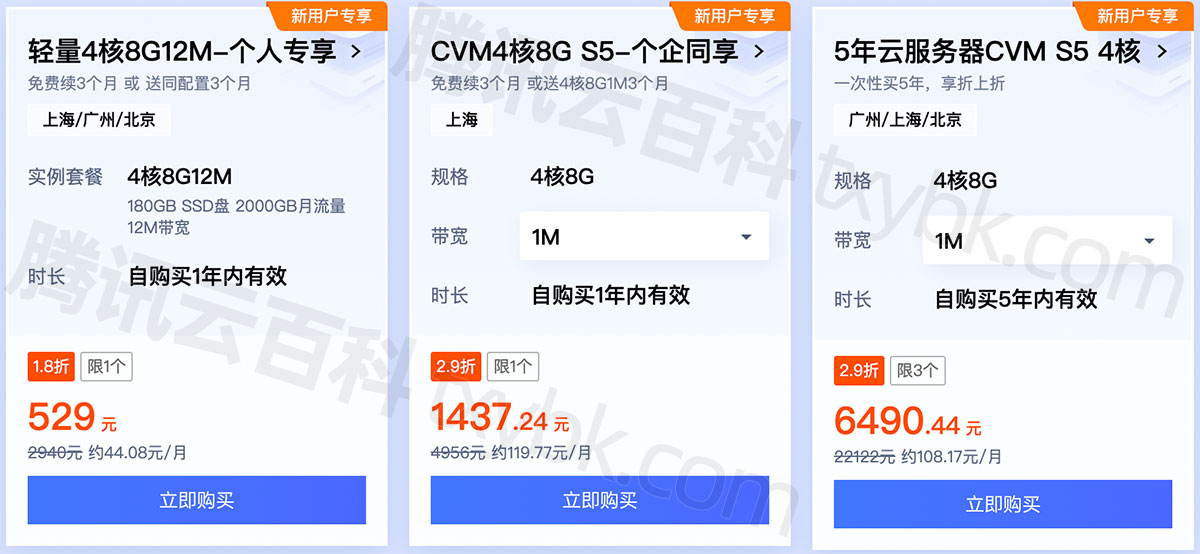
腾讯云4核8G服务器多少钱?2024精准报价
腾讯云4核8G服务器S5和轻量应用服务器优惠价格表,轻量应用服务器和CVM云服务器均有活动,云服务器CVM标准型S5实例4核8G配置价格15个月1437.3元,5年6490.44元,标准型SA2服务器1444.8元一年,轻量应用服务器4核8G12M带宽一…...
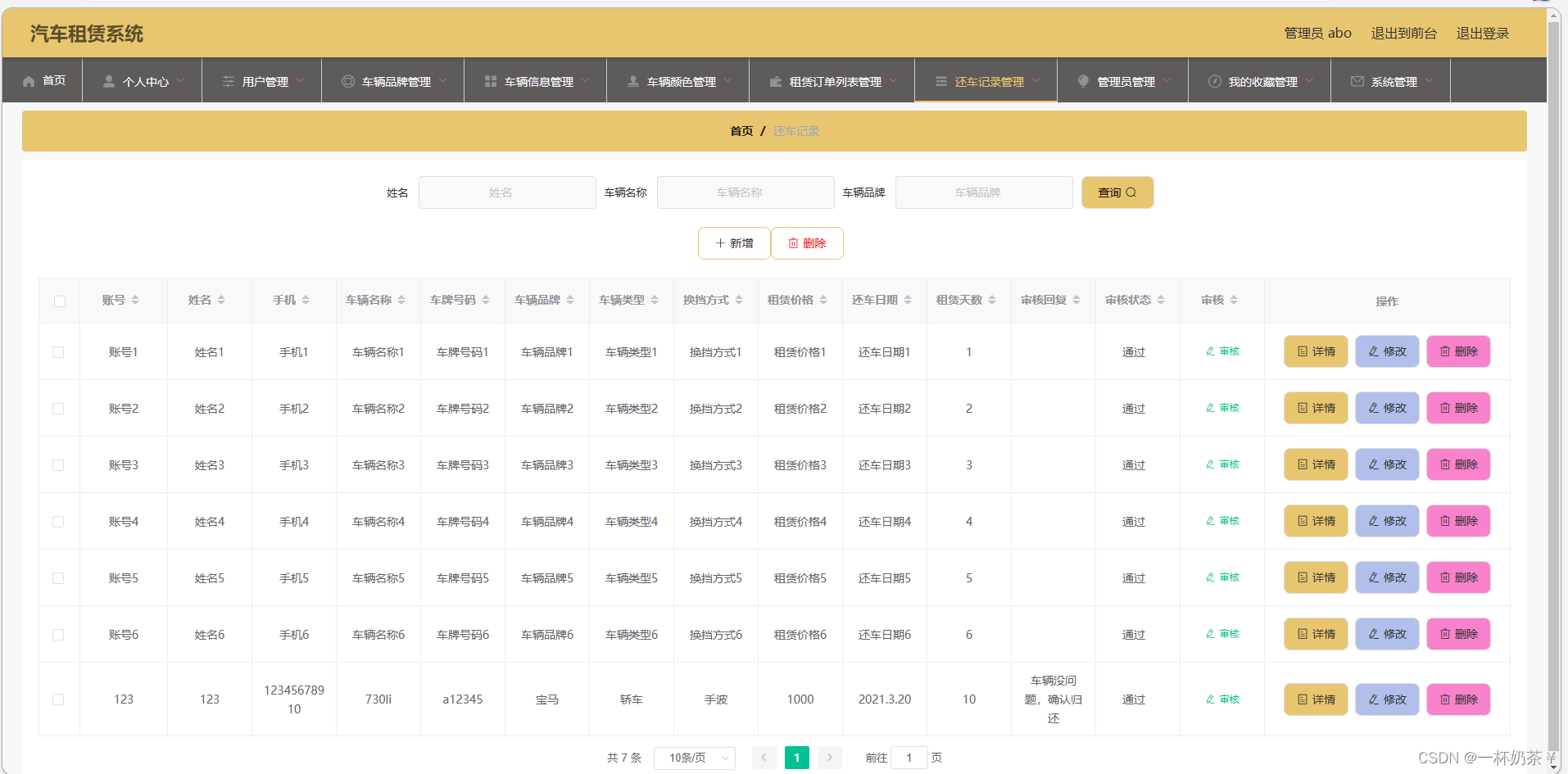
汽车出租管理系统
文章目录 汽车出租管理系统一、系统演示二、项目介绍三、系统部分功能截图四、部分代码展示五、底部获取项目源码(9.9¥带走) 汽车出租管理系统 一、系统演示 汽车租赁系统 二、项目介绍 语言:java 框架:SpringBoot、…...

使用SM4国密加密算法对Spring Boot项目数据库连接信息以及yaml文件配置属性进行加密配置(读取时自动解密)
一、前言 在业务系统开发过程中,我们必不可少的会使用数据库,在应用开发过程中,数据库连接信息往往都是以明文的方式配置到yaml配置文件中的,这样有密码泄露的风险,那么有没有什么方式可以避免呢?方案当然是有的,就是对数据库密码配置的时候进行加密,然后读取的时候再…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
