随机过程及应用学习笔记(二)随机过程的基本概念
随机过程论就是研究随时间变化的动态系统中随机现象的统计规律的一门数学学科。
目录
前言
一、随机过程的定义及分类
1、定义
2、分类
二、随机过程的分布及其数字特征
1、分布函数
2、数字特征
均值函数和方差函数
协方差函数和相关函数
3、互协方差函数与互相关函数
三、复随机过程
总结
前言
随机过程理论产生于本世纪初,起源于统计物理学领域。布朗运动和热噪声是随机过程的最早例子。随机过程理论在社会科学、自然科学和工程技术的各个领域中都有着广泛的应用。例如:现代电子技术、现代通讯、自动控制、系统工程的可靠性工程、市场经济的预测和控制、随机服务系统的排队论﹑储存论、生物医学工程、人口的预测和控制等等。只要人们要研究随时间变化的动态系统的随机现象的统计规律时,就要应用到随机过程的理论。
一、随机过程的定义及分类
1、定义
随机过程可以形式化地定义为一个随机变量的集合 {X(t), t ∈ T},其中 T 是一个表示时间的参数集合。对于每个时间点 t ∈ T,X(t) 是一个随机变量,表示在该时间点上观察到的随机现象的取值。这样的集合 {X(t), t ∈ T} 被称为随机过程。
在实际应用中,随机过程通常分为离散时间和连续时间两种情况。如果参数集合 T 是离散的,那么随机过程是离散时间随机过程;如果参数集合 T 是连续的,那么随机过程是连续时间随机过程。
随机过程的性质可以通过其概率分布、相关性函数、平均值等统计量来描述,这些性质可以用来分析随机过程的行为和特征。 常见的随机过程包括布朗运动、泊松过程、马尔可夫过程等。

说明:{X(t,),t e T}
- 参数集T在实际问题中,常常指的是时间参数,但有时也用其它物理量作为参数集。
- X(t,o)是定义在T×Q上的二元函数。
- t固定时,X(t,o)是随机变量。o固定时,X(t,o)是T的样本函数。
- 随机过程{X(t),t aT}是时刻t上的取值x,称为状态,状态的全体称为状态空间。记为:E={x : X(t)=x,t eT}
2、分类
按状态空间和参数集分类:

按概率分布规律分类:随机过程{X(t),t∈ T}按其概率分布规律分为:独立过程、独立增量过程、正态过程﹑泊松过程、维纳过程﹑平稳过程和马尔可夫过程等等。
二、随机过程的分布及其数字特征
1、分布函数
一维分布函数和一维概率密度是用来描述随机变量的统计性质的工具。它们是概率论中的基本概念,用于描述随机变量在不同取值上的概率分布。
一维分布函数 (Cumulative Distribution Function, CDF):
- 一维分布函数是一个函数,表示随机变量小于或等于某个特定取值的累积概率。
- 用 F(x) 表示,其中 x 是随机变量的某个具体取值。
- 公式:F(x)=P(X≤x)
- 分布函数具有以下性质:
- 0≤F(x)≤1 对所有 x 成立。
- F(x) 是非递减函数,即对于 x1<x2,有 F(x1)≤F(x2)。
- 当x→−∞ 时,F(x)→0,当 x→+∞ 时,F(x)→1。
一维概率密度 (Probability Density Function, PDF):
- 一维概率密度是一个函数,表示随机变量在某个取值附近的概率密度。
- 用 f(x) 表示,其中 x 是随机变量的某个具体取值。
- 公式:f(x)=dxdF(x)
- 概率密度具有以下性质:
- 对于所有 x,f(x)≥0。
- 在整个实轴上的积分等于 1,即∫−∞+∞f(x)dx=1。
- 在某个区间上的概率可以通过概率密度函数在该区间上的积分来计算。
在实际应用中,分布函数和概率密度函数是用来描述随机变量在不同取值上的概率分布特征的重要工具,它们在统计学、概率论、以及随机过程的分析中都有广泛的应用。
二维分布函数 (Joint Cumulative Distribution Function, Joint CDF):
- 对于两个随机变量 X 和 Y,二维分布函数F(x,y) 表示这两个变量小于或等于给定取值的联合累积概率。
- 公式:F(x,y)=P(X≤x,Y≤y)
- 二维分布函数具有类似一维分布函数的性质,包括非递减性和在边界处的收敛性。
二维概率密度 (Joint Probability Density Function, Joint PDF):
- 对于两个随机变量 X 和 Y,二维概率密度函数 f(x,y) 表示在给定点 (x,y) 处的联合概率密度。
- 公式:f(x,y)=∂x∂y∂2F(x,y)
- 二维概率密度函数具有以下性质:
- 对于所有 x 和 y,f(x,y)≥0。
- 在整个二维空间上的积分等于1,即 ∬−∞+∞f(x,y)dxdy=1。
- 对于任意二维区域 A,该区域上的概率可以通过概率密度函数在该区域上的二重积分来计算。
N维分布函数和N维概率密度函数用于描述多个(N个)随机变量的联合概率分布。它们是概率论和统计学中的基本概念,用于研究多个随机变量之间的关系以及它们在不同取值上的概率分布。
N维分布函数 (Joint Cumulative Distribution Function, Joint CDF):
- 对于N个随机变量 X1,X2,…,XN,N维分布函数 F(x1,x2,…,xN) 表示这些变量小于或等于给定取值的联合累积概率。
- 公式:F(x1,x2,…,xN)=P(X1≤x1,X2≤x2,…,XN≤xN)
- N维分布函数具有类似于一维和二维分布函数的性质,包括非递减性和在边界处的收敛性。
N维概率密度函数 (Joint Probability Density Function, Joint PDF):
- 对于N个随机变量 X1,X2,…,XN,N维概率密度函数f(x1,x2,…,xN) 表示在给定点 (x1,x2,…,xN) 处的联合概率密度。
- 公式:f(x1,x2,…,xN)=∂x1∂x2…∂xN∂NF(x1,x2,…,xN)
- N维概率密度函数具有类似于一维和二维概率密度函数的性质,包括非负性和在整个N维空间上的积分等于1。
N+M维分布函数和N+M维概率密度函数是用于描述两组随机变量的联合概率分布。假设有N个变量组成的随机向量 X=(X1,X2,…,XN) 和M个变量组成的随机向量 Y=(Y1,Y2,…,YM),则N+M维分布函数和N+M维概率密度函数描述的是这两组随机变量在一起的联合分布。
N+M维分布函数 (Joint Cumulative Distribution Function, Joint CDF):
- 对于随机向量 X 和 Y,N+M维分布函数 F(x1,x2,…,xN,y1,y2,…,yM) 表示这两个随机向量中的每一个分量小于或等于相应的给定取值的联合累积概率。
- 公式:F(x1,x2,…,xN,y1,y2,…,yM)=P(X1≤x1,X2≤x2,…,XN≤xN,Y1≤y1,Y2≤y2,…,YM≤yM)
N+M维概率密度函数 (Joint Probability Density Function, Joint PDF):
- 对于随机向量 X 和 Y,N+M维概率密度函数f(x1,x2,…,xN,y1,y2,\ldous,yM) 表示在给定点 (x1,x2,…,xN,y1,y2,…,yM) 处的联合概率密度。
- 公式:f(x1,x2,…,xN,y1,y2,…,yM)=∂x1∂x2…∂xN∂y1∂y2…∂yM∂N+MF(x1,x2,…,xN,y1,y2,…,yM)
两个随机过程相互独立意味着它们之间的任何一对随机变量都是独立的。如果有两个随机过程 X(t) 和 Y(t),它们在每个时间点上都有一个随机变量值,那么这两个随机过程相互独立意味着对于任意时刻 t1,t2,…,tn,对应的随机变量X(t1),X(t2),…,X(tn) 与Y(t1),Y(t2),…,Y(tn) 是独立的。
形式化地,两个随机过程 X(t) 和 Y(t) 相互独立可以表示为:
P(X(t1)≤x1,X(t2)≤x2,…,X(tn)≤xn,Y(t1)≤y1,Y(t2)≤y2,…,Y(tn)≤yn) =P(X(t1)≤x1)⋅P(X(t2)≤x2)⋅…⋅P(X(tn)≤xn)⋅P(Y(t1)≤y1)⋅P(Y(t2)≤y2)⋅…⋅P(Y(tn)≤yn)
有限维度特征函数族:
特征函数是概率论中用于描述随机变量分布的一种函数。有限维度特征函数族指的是一个包含有限维度特征函数的集合,通常用于表示多维随机变量的联合分布。
对于一个N维随机向量X=(X1,X2,…,XN),其特征函数定义为:
ϕ(t1,t2,…,tN)=E[ei(t1X1+t2X2+…+tNXN)]
其中 i 是虚数单位。有限维度特征函数族是指由上述特征函数组成的集合,其中 t1,t2,…,tN 可以取任意实数。
分布函数的对称性和相容性:
-
对称性 (Symmetry):
- 如果随机变量 X 的分布函数 FX(x) 满足FX(x)=FX(−x) 对于所有的 x 成立,那么称 X 具有对称分布。这表示分布关于原点对称。
-
相容性 (Compatibility):
- 如果随机变量 X 和 Y 的分布函数分别为FX(x) 和FY(y),那么 X 和 Y 被称为相容的,如果对于所有实数 a 和 b,下面的等式成立:P(aX+b≤y)=FY(ay−b)
- 这表示对于任意实数a 和 b,通过仿射变换aX+b,从 X 的分布可以得到 Y 的分布。
对称性和相容性是概率论中常见的性质,它们在分析随机变量的性质和特征时非常有用。具有对称性的分布在某些情况下能够简化分析,而相容性则提供了一种从一个分布到另一个分布的变换方式。

2、数字特征
大部分随机过程的分布函数难以得到。研究随机过程的数字特征,可以反映出随机过程的局部统计特性。
均值函数和方差函数
均值函数和方差函数是统计学中常用的两个概念,它们用于描述数据分布的特征。
-
均值函数(Mean Function): 均值函数是一种统计量,通常表示一组数据的平均值。计算均值的方法是将所有数据相加,然后除以数据的总个数。均值是数据分布的中心趋势的一种度量,它对于了解数据集中的典型值很有帮助。均值的数学表示为:

其中,xi 表示数据集中的第i个数据点,n 表示数据点的总个数。
-
方差函数(Variance Function): 方差是一种度量数据分散程度的统计量。方差衡量每个数据点与均值的偏离程度,计算方法是将每个数据点与均值的差值的平方相加,然后除以数据点的总个数。方差越大,说明数据点相对于均值的偏离程度越大。方差的数学表示为:
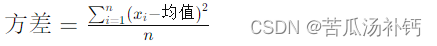
其中,xi 表示数据集中的第i个数据点,均值均值 表示数据的均值,n 表示数据点的总个数。
这两个统计量在分析和描述数据集特征时经常被使用。均值关注数据的中心趋势,而方差关注数据的分散程度。在统计学中,这两者常常一起使用来全面了解数据的分布情况。
在随机过程中,均值函数(Mean Function)和方差函数(Variance Function)描述了随机变量随时间的变化规律。
-
随机过程的均值函数: 随机过程的均值函数表示随机变量在不同时间点的平均值。对于一个离散时间的随机过程,均值函数可以用以下形式表示:
μ(t)=E[X(t)]
其中,X(t) 是随机过程在时刻t 的随机变量,μ(t) 表示在时刻 t 的均值函数,E[⋅] 表示期望运算符。均值函数描述了随机过程在不同时间点的平均趋势。
-
随机过程的方差函数: 随机过程的方差函数表示随机变量在不同时间点的方差。对于一个离散时间的随机过程,方差函数可以用以下形式表示:

其中,X(t) 是随机过程在时刻 t 的随机变量,σ2(t) 表示在时刻 t 的方差函数,Var[⋅] 表示方差运算符。方差函数描述了随机过程在不同时间点的波动性或分散程度。
这些函数对于理解随机过程的特性和性质非常重要。它们提供了关于随机变量随时间演化的一些基本统计信息,有助于建立模型、预测未来状态以及进行随机过程的分析。在实际应用中,通常需要通过采样或模拟来估计这些函数,因为真实的随机过程可能无法直接观测。
均方差函数(Mean-Square Function): 均方差函数是一个衡量随机过程在不同时间点的均方差(平均方差)的函数。对于一个随机过程 X(t),其均方差函数通常用以下形式表示:
![]()
其中,RX(t,τ) 表示在时刻 t 和 t+τ 的均方差函数,E[⋅] 表示期望运算符。均方差函数测量了不同时刻的随机变量之间的平方关系。
协方差函数和相关函数
-
协方差函数(Covariance Function): 协方差函数描述了随机过程在不同时间点的协方差。对于一个随机过程 X(t),其协方差函数通常用以下形式表示:

协方差函数可以用来研究随机过程中不同时刻的随机变量之间的线性关系。
-
相关函数(Correlation Function): 相关函数是一种描述随机过程中不同时刻随机变量之间相关性的函数。对于一个随机过程 X(t),其相关函数通常用以下形式表示:

其中,ρX(t,τ) 表示在时刻 t 和 t+τ 的相关函数,CX(t,τ) 是协方差函数,RX(t,0) 和 RX(t+τ,0) 是均方差函数。
3、互协方差函数与互相关函数
随机过程的互协方差函数和互相关函数描述了两个不同随机过程之间的关系,而不是同一个随机过程在不同时间点的关系。
-
互协方差函数(Cross-Covariance Function): 互协方差函数是用于描述两个不同随机过程之间协方差的函数。如果有两个随机过程 X(t) 和Y(t),它们在时刻 t 和 t+τ 的互协方差函数通常表示为:
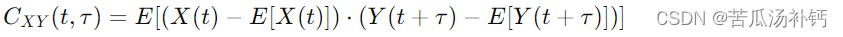
这个函数测量了两个随机过程在不同时刻的随机变量之间的线性关系。
-
互相关函数(Cross-Correlation Function): 互相关函数是用于描述两个不同随机过程之间相关性的函数。如果有两个随机过程 X(t) 和 Y(t),它们在时刻 t 和 t+τ 的互相关函数通常表示为:

其中,CXY(t,τ) 是互协方差函数,RX(t,0) 和 RY(t+τ,0) 分别是 X(t) 和 Y(t) 的均方差函数。
三、复随机过程
复随机过程是一种随机过程,其样本函数(随机过程的每个具体实现)的值是复数。与实数值的随机过程不同,复随机过程的样本函数在每个时间点处都取复数值。
复随机过程通常用以下形式表示:
X(t,ω):Ω×T→C
其中,X(t,ω) 是复随机过程的样本函数,Ω 是样本空间,T 是时间集合,ω 是样本点,t 是时间。复随机过程的样本函数在每个时间点 t 处都可以是一个复数。
复随机过程的理论涉及到复数域上的概率空间和概率测度。与实随机过程相比,复随机过程在信号处理、通信系统、量子力学等领域中具有重要的应用,因为它们能够更灵活地表示和处理具有复数值的随机信号和随机过程。例如,在通信系统中,信号往往是复数值的,因此复随机过程的理论更适合用来建模和分析这类信号的统计特性。

总结
随机过程是描述随机现象随时间变化的数学模型。简而言之,它是一组随机变量的集合,这些随机变量的取值取决于某种随机规律,并且通常是关于时间的函数。随机过程是概率论和统计学中的重要概念,被广泛应用于模拟、风险分析、信号处理、金融工程等领域。
相关文章:

随机过程及应用学习笔记(二)随机过程的基本概念
随机过程论就是研究随时间变化的动态系统中随机现象的统计规律的一门数学学科。 目录 前言 一、随机过程的定义及分类 1、定义 2、分类 二、随机过程的分布及其数字特征 1、分布函数 2、数字特征 均值函数和方差函数 协方差函数和相关函数 3、互协方差函数与互相关函…...

【机器学习】Kmeans如何选择k值
确定 K 值是 K-means 聚类分析的一个重要步骤。不同的 K 值可能会产生不同的聚类结果,因此选择合适的 K 值非常重要。 以下是一些常见的方法来选择 K 值: 手肘法:该方法基于绘制聚类内误差平方和(SSE)与 K 值之间的关系图。随着 K 值的增加,SSE会逐渐降低,但降低幅度逐…...
)
LeetCode 热题 100 | 链表(下)
目录 1 148. 排序链表 2 23. 合并 K 个升序链表 3 146. LRU 缓存 3.1 解题思路 3.2 详细过程 3.3 完整代码 菜鸟做题第三周,语言是 C 1 148. 排序链表 解题思路: 遍历链表,把每个节点的 val 都存入数组中用 sort 函数对数组进…...

Ubuntu搭建计算集群
计算机硬件和技术的发展使得高性能模拟和计算在生活和工作中的作用逐渐显现出来,无论是计算化学,计算物理和当下的人工智能都离不开高性能计算。笔者工作主要围绕计算化学和物理开展,亦受限于自身知识和技术所限,文中只是浅显地尝…...

数据结构~~树(2024/2/8)
目录 树 1、定义: 2、树的基本术语: 3、树的表示 树 1、定义: 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树&…...
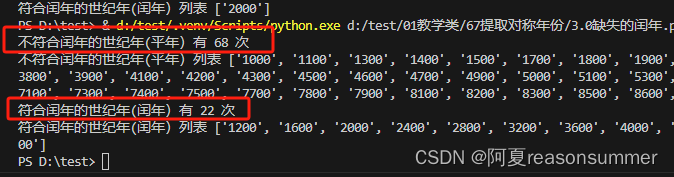
【教学类-48-03】202402011“闰年”(每4年一次 2月有29日)世纪年必须整除400才是闰年)
2000-2099年之间的闰年有25次, 背景需求: 已经制作了对称年月的数字提取,和年月日相等的年份提取 【教学类-48-01】20240205对称的“年”和“月日”(如2030 0302)-CSDN博客文章浏览阅读84次。【教学类-48-01】202402…...

如何开发一个属于自己的人工智能语言大模型?
要开发一个属于自己的人工智能语言模型,你需要遵循以下步骤: 数据收集:首先你需要大量的文本数据来训练你的模型。这些数据可以来自于各种来源,例如书籍、网站、新闻文章等。你需要确保这些数据足够多样化,以便模型能学…...

【HTTP】localhost和127.0.0.1的区别是什么?
目录 localhost是什么呢? 从域名到程序 localhost和127.0.0.1的区别是什么? 域名的等级划分 多网站共用一个IP和端口 私有IP地址 IPv6 今天在网上逛的时候看到一个问题,没想到大家讨论的很热烈,就是标题中这个: …...

Edge浏览器-常用快捷键
按键组合作用Ctrl Shift I开发人员工具Ctrl E定位到 空地址栏Ctrl L定位到 地址栏Ctrl Shift B显示或隐藏 收藏夹栏Ctrl Shift O打开收藏夹(搜索)Ctrl T打开一个新标签页Ctrl W关闭当前标签页Ctrl Shift T重新打开刚才关闭的标签页Ctrl Tab切换到下一个标签页Ctrl…...

C++:Vector动态数组的copy深入理解
动态数组分配的大小默认为2的n次方1,2,4,8... 在main中创建的vertices,push需要放到Vertex中(copy),下一次copy是因为要调整vertices的大小 vertices.push_back(Vertex(1,2,3));//拷贝 第一次&a…...
切片操作)
【PyTorch】PyTorch中张量(Tensor)切片操作
PyTorch深度学习总结 第三章 PyTorch中张量(Tensor)切片操作 文章目录 PyTorch深度学习总结一、前言二、获取张量中的元素1、切片(行、列数)方法2、torch.where()函数3、使元素置零的操作 一、前言 上文介绍了PyTorch中改变张量(Tensor)形状的操作&…...
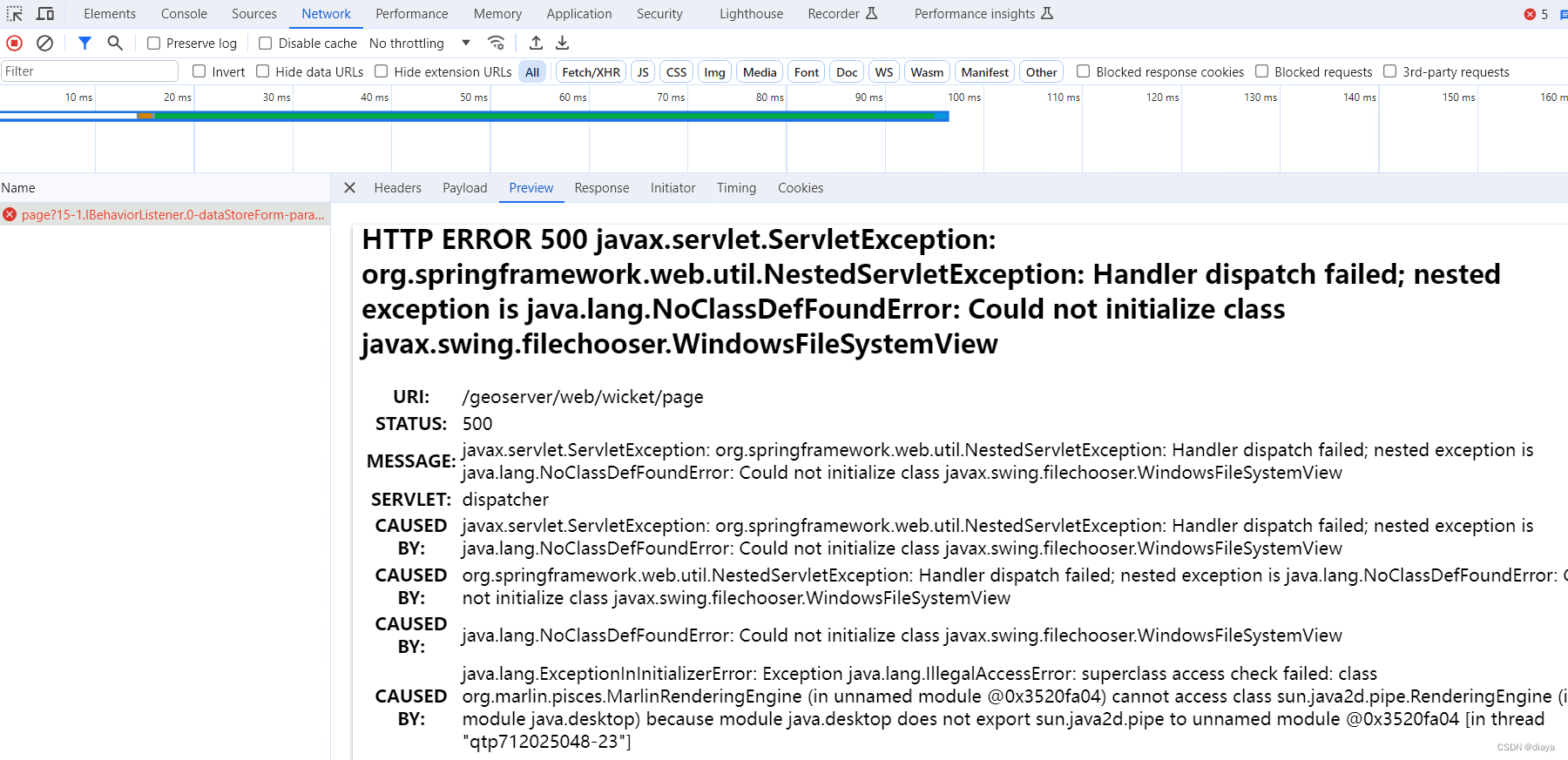
GeoServer 2.11.1升级解决Eclipse Jetty 的一系列安全漏洞问题
Eclipse Jetty 资源管理错误漏洞(CVE-2021-28165) Eclipse Jetty HTTP请求走私漏洞(CVE-2017-7656) Eclipse Jetty HTTP请求走私漏洞(CVE-2017-7657) Eclipse Jetty HTTP请求走私漏洞(CVE-2017-7658) Jetty 信息泄露漏洞(CVE-2017-9735) Eclipse Jetty 安全漏洞(CVE-2022-20…...

【蓝桥杯选拔赛真题34】C++最大值 第十三届蓝桥杯青少年创意编程大赛C++编程选拔赛真题解析
目录 C/C++最大值 一、题目要求 1、编程实现 2、输入输出...
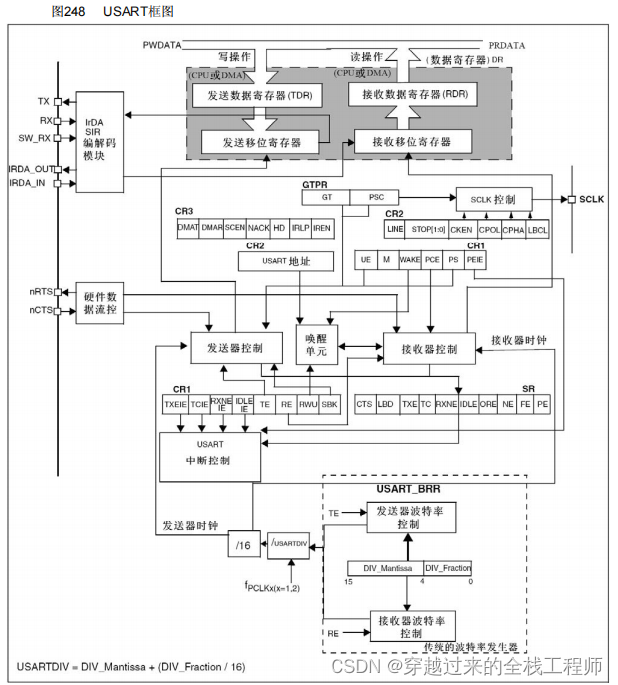
STM32之USART
概述 串口通信,通用异步收发传输器(Universal Asynchronous Receiver/Transmitter ),简称UART;而USART(Universal Synchronous/Asynchronous Receiver/Transmitter)通用同步收发传输器。 USAR…...
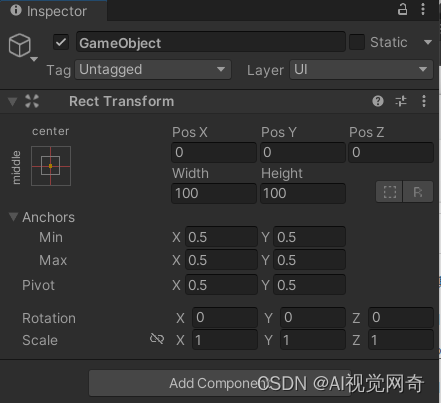
unity 点击事件
目录 点击按钮,显示图片功能教程 第1步添加ui button,添加ui RawImage 第2步 添加脚本: 第3步,把脚本拖拽到button,点击button,设置脚本的变量, GameObject添加 Component组件 点击按钮&am…...
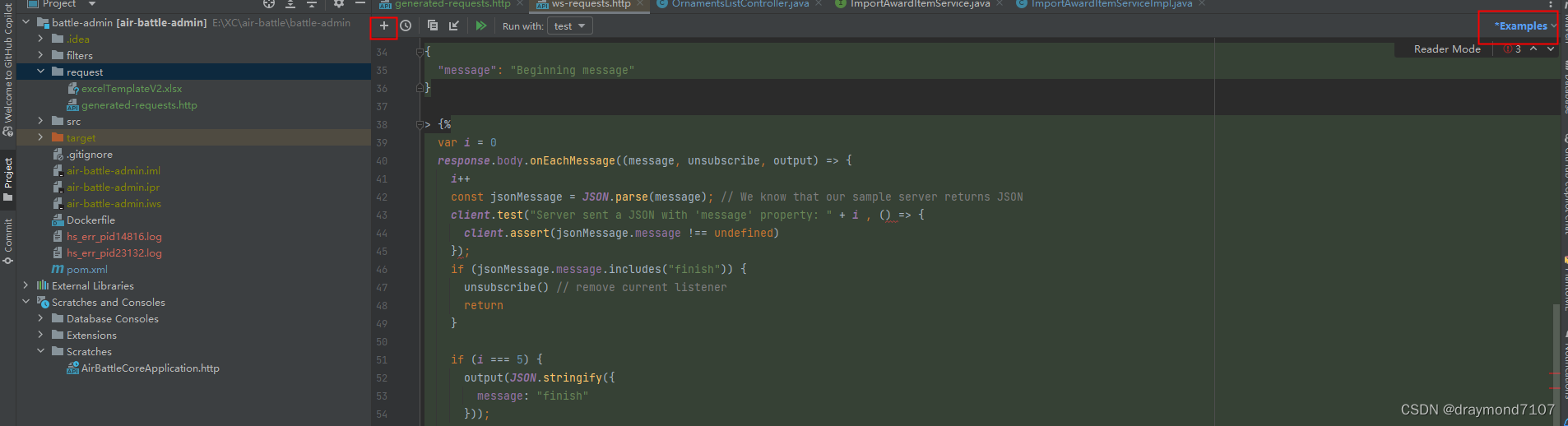
idea自带的HttpClient使用
1. 全局变量配置 {"local":{"baseUrl": "http://localhost:9001/"},"test": {"baseUrl": "http://localhost:9002/"} }2. 登录并将结果设置到全局变量 PostMapping("/login")public JSONObject login(H…...
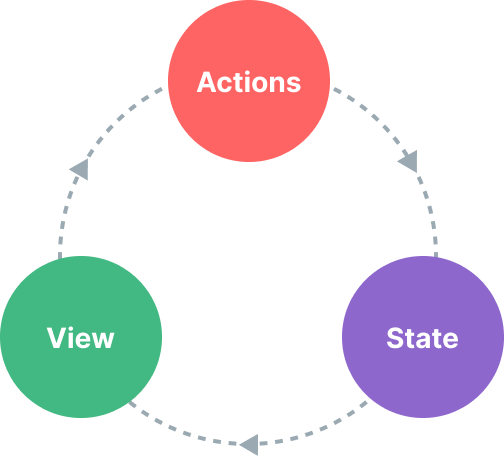
vue3-应用规模化-路由和状态
客户端 vs. 服务端路由 服务端路由指的是服务器根据用户访问的 URL 路径返回不同的响应结果。当我们在一个传统的服务端渲染的 web 应用中点击一个链接时,浏览器会从服务端获得全新的 HTML,然后重新加载整个页面。 然而,在单页面应用中&…...
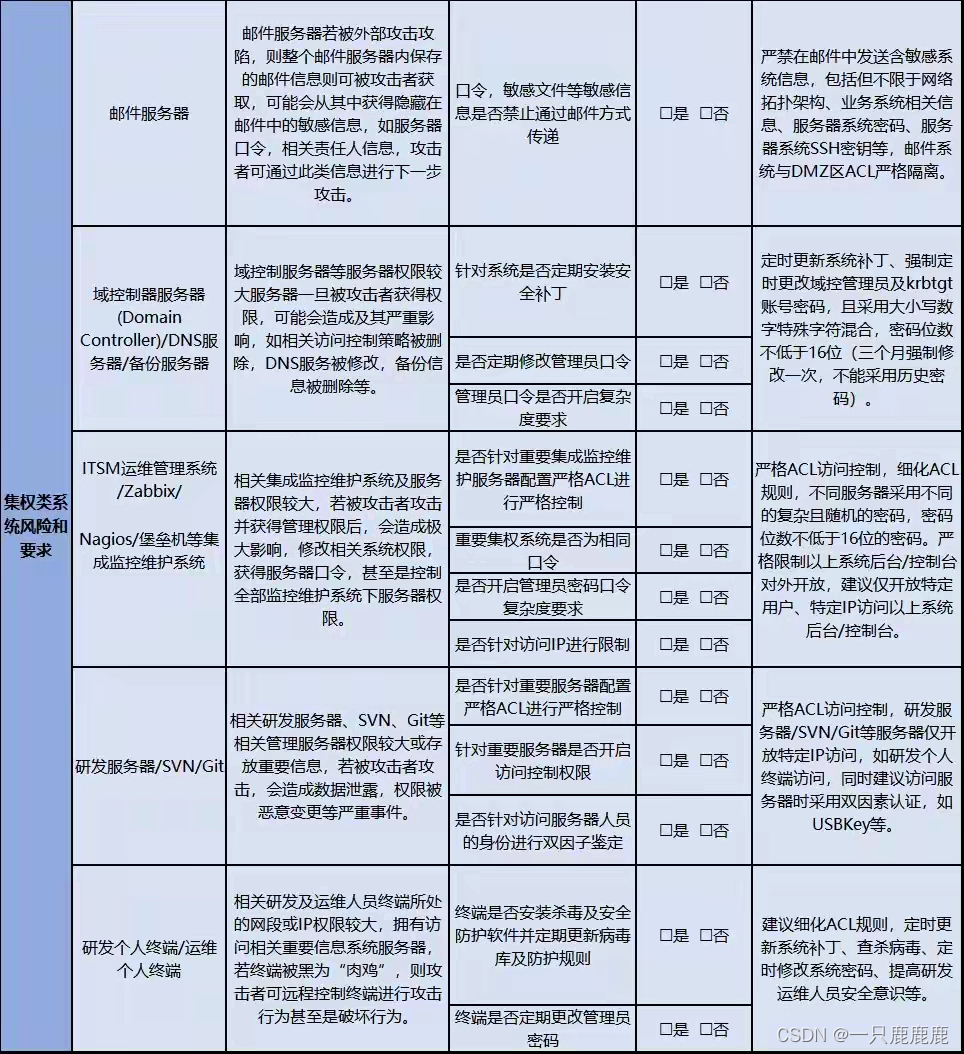
网络安全检查表
《网络攻击检查表》 1.应用安全漏洞 2.弱口令,默认口令 3.服务器互联网暴露 4.操作系统,中间件安全漏洞 5.研发服务器,邮件服务器等安全检查...
)
SSM框架,Maven的学习(下)
依赖传递和依赖冲突 依赖传递指的是当一个模块或库 A 依赖于另一个模块或库 B,而 B 又依赖于模块或库 C,那么 A 会间接依赖于 C。这种依赖传递结构可以形成一个依赖树。当我们引入一个库或框架时,构建工具(如 Maven、Gradle&…...

Vivado开发FPGA使用流程、教程 verilog(建立工程、编译文件到最终烧录的全流程)
目录 一、概述 二、工程创建 三、添加设计文件并编译 四、线上仿真 五、布局布线 六、生成比特流文件 七、烧录 一、概述 vivado开发FPGA流程分为创建工程、添加设计文件、编译、线上仿真、布局布线(添加约束文件)、生成比特流文件、烧录等步骤&a…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
