FlinkSql通用调优策略
历史文章迁移,稍后整理
使用DataGenerator 提前进行压测,了解数据的处理瓶颈、性能测试和消费能力
开启minibatch:"table.exec.mini-batch.enabled", "true"
开启Local+Global 两阶段聚合:"table.exec.mini-batch.enabled", "true"
解决数据倾斜问题:
流式倾斜,开启minibatch
窗口类有界操作,传统的两阶段聚合的方式
数据源分布就不均匀,做reblance
针对大状态开启rocksdb
针对分区无数据导致watermark的窗口等不触发,设置idle
利用paimon做中间存储,既可以做批流复用olap,lookup join 时把全量数据拉到rocksdb并且是分片存的,效率很高,缺点是有延迟,会有join key miss的问题
暴力调优,加内存,调大并行度
设置空闲 State 保留时间 ,看情况,设置不当会影响结果正确性
FlinkSql 可以指定空闲状态(即未更新的状态)被保留的最小时间,当状态中的某个 Key 对应的状态未更新的时间达到阈值时,这条状态会被自动清理
4.2 开启 MiniBatch
Flink 是流式数据处理,没过来一条数据就会被直接处理
MiniBatch 是把流处理变为微批处理的方式,先缓存一定的数据后在触发处理,这样可以减少对 State 的访问、提升吞吐、有效减少输出数据量
但是会牺牲低延迟,对超低延迟要求的场景不建议用,常用在需要聚合的场景,有显著的性能提升
// 开启 miniBatch
configuration.setString("table.exec.mini-batch.enabled", "true");
// 批量输出的间隔时间
configuration.setString("table.exec.mini-batch.allow-latency", "5 s");
// 防止 OOM 设置每个批次最多缓存数据的条数,可以设为 2 万条
configuration.setString("table.exec.mini-batch.size", "20000");主要是依靠每个 Task 上注册的 Timer 线程(Flink 的定时器)来触发微批,当然了,是需要消耗一定的线程性能
4.3 开启 LocalGlobal
其实就是本地聚合(Spark 的 reduceByKey 和 MR 的 Combine),所以开启 LocalGlobal 必须开启 MiniBatch,可以有效解决SUM的那个聚合函数数据倾斜的问题,同时还能优化上游对下游的数据传输、以及下游聚合的压力
// 开启 LocalGlobal
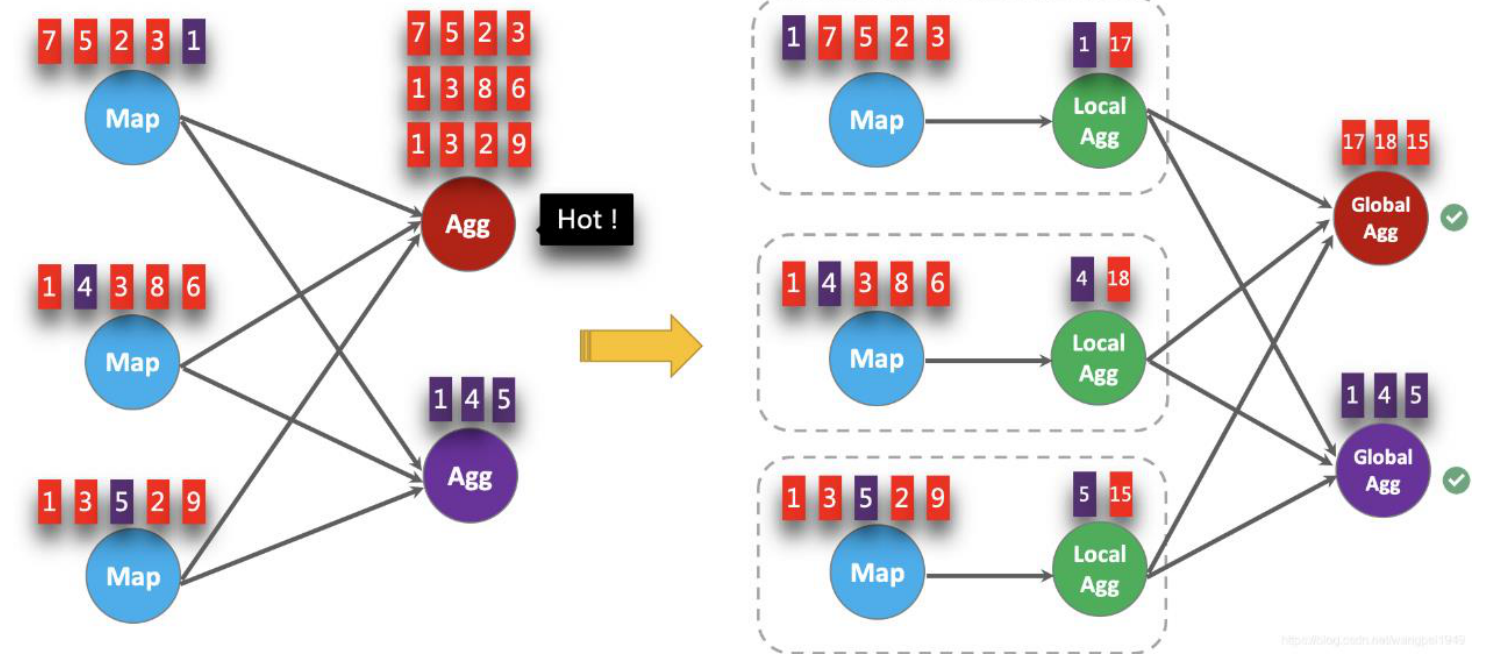
configuration.setString("table.optimizer.agg-phase-strategy", "TWO_PHASE");如下图,红色和紫色分别代表两个 Key 的数据进行聚合时的效果
4.4 开启 Split Distinct
LocalGlobal 的方式可以有效解决 SUM 等聚合函数数据倾斜的问题,但是对于 Group 后的 Count ( Distinct )的热点问题没法解决
1. 以前我们手动打散的方案
SELECT a, SUM(cnt)
FROM (
SELECT a, COUNT(DISTINCT b) as cnt
FROM T
GROUP BY a, MOD(HASH_CODE(b), 1024)
)
GROUP BY a2. FlinkSql 自动实现了这部分功能,只需要我们开启 Split Distinct 参数即可
// 设置参数:(要结合 minibatch 一起使用)
// 开启 Split Distinct
configuration.setString("table.optimizer.distinct-agg.split.enabled", "true");
// 第一层打散的 bucket 数目
configuration.setString("table.optimizer.distinct-agg.split.bucket-num", "1024");原理如下图,红色和紫色仍然分别代表两个 Key 的数据,但是红色的数据显然很多,但是去重必须同一个 Key 的数据肯定在一个节点,所以压力较大
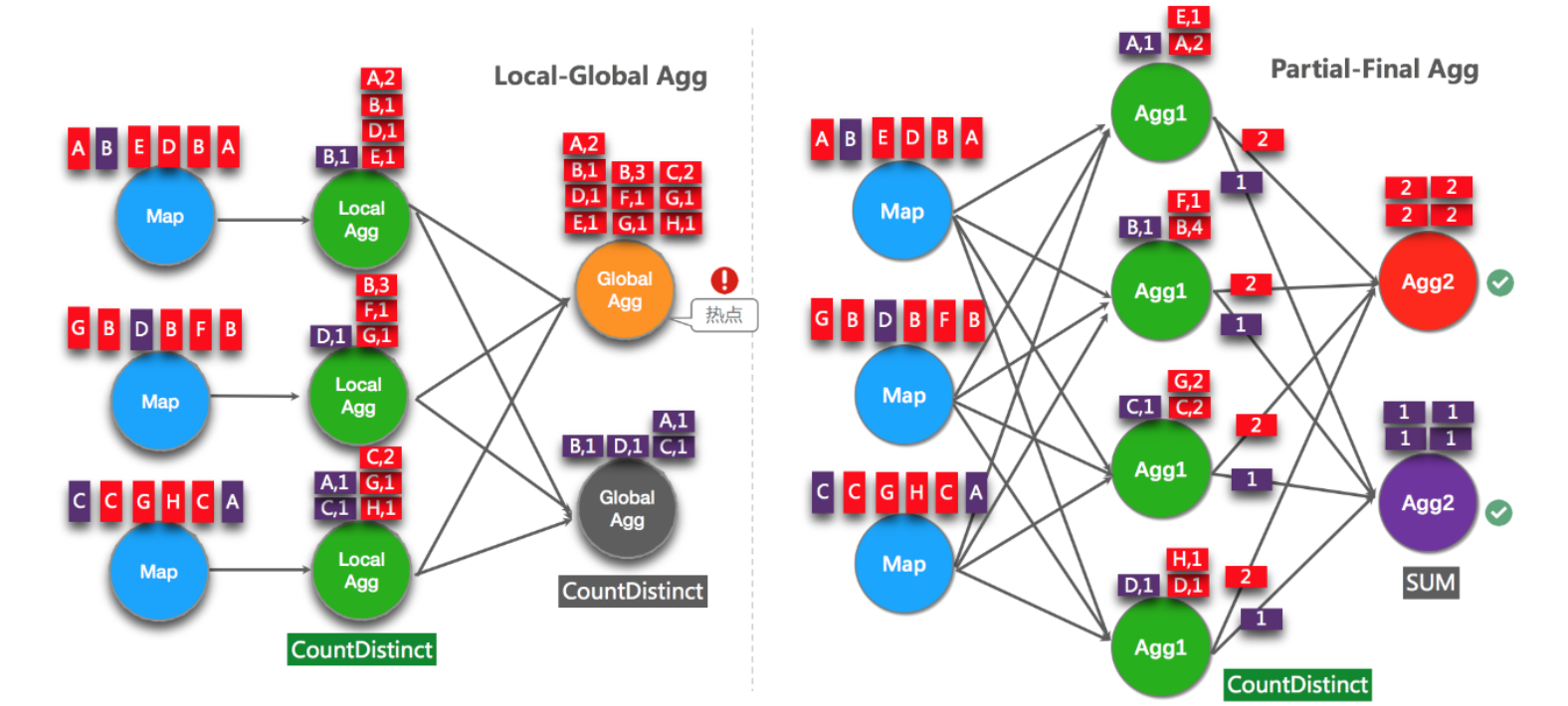
4.5 Count ( Distinct ) 时可以用 Filter 代替 Case When
我们经常会写这样的 Sql,如下会有 3 个状态实例
SELECT
a,
COUNT(DISTINCT b) AS total_b,
COUNT(DISTINCT CASE WHEN c IN ('A', 'B') THEN b ELSE NULL END) AS AB_b,
COUNT(DISTINCT CASE WHEN c IN ('C', 'D') THEN b ELSE NULL END) AS CD_b
FROM T
GROUP BY a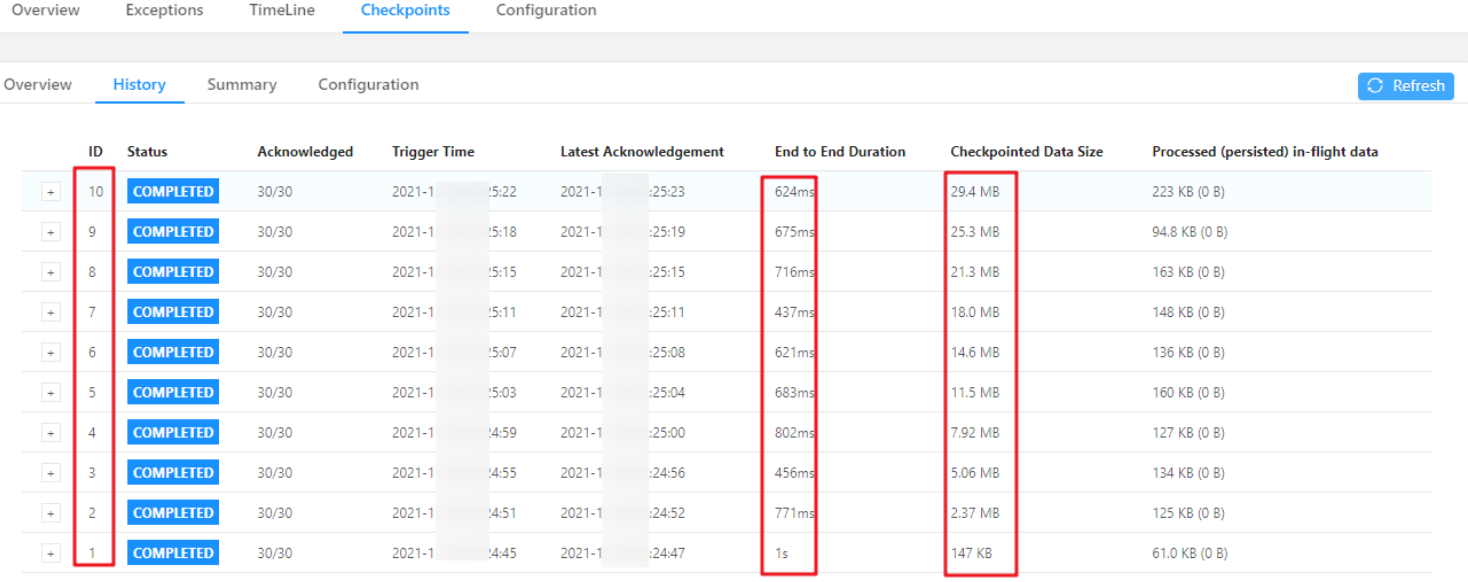
而 FlinkSql 的优化器可以识别同一唯一键的不同 Filter 参数,三个 COUNT DISTINCT 都作用在 b 列上,我们可以利用 Filter 的这一特性,Flink 可以只使用一个共享状态实例,可减少状态的大小和对状态的访问
SELECT
a,
COUNT(DISTINCT b) AS total_b,
COUNT(DISTINCT b) FILTER (WHERE c IN ('A', 'B')) AS AB_b,
COUNT(DISTINCT b) FILTER (WHERE c IN ('C', 'D')) AS CD_b
FROM T
GROUP BY a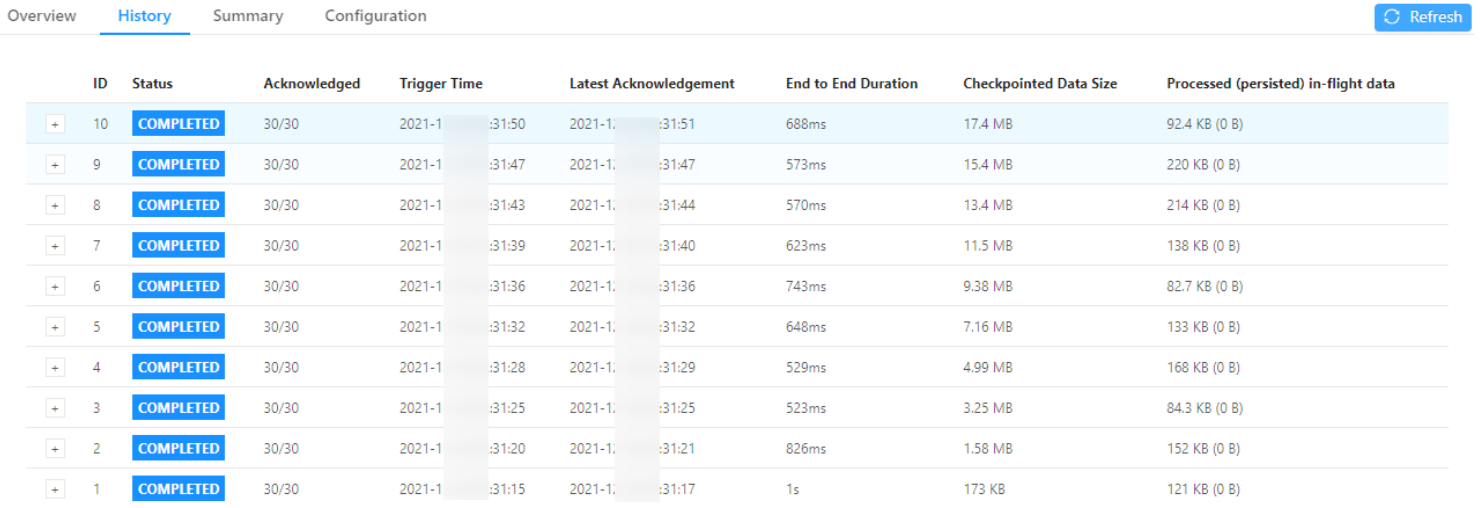
解决数据倾斜、反压问题
lookup join 的优化,避免性能较差的热查询
paimon属于链路的优化,既可以数据重用,重写了lookup join 减少checkpoint压力,缺点是...
FlinkSql window tvf 本身也是一种优化
当使用细粒度的滑动窗口(窗口长度远远大于滑动步长)时,重叠的窗口过多,一个数据会属于多个窗口,性能会急剧下降
比如 24h 的窗口,3分钟滑动一次,那么粒度就是 24 * 60 / 3 = 480 ,会导致两个问题
1. 状态
对于一个元素,将其对应的(key,window)写入 WindowState,那意味着每个元素到来,更新 WindowState 时都要遍历 480 个窗口然后写入,开销很大,即使用 RocksDBStateBackend 瓶颈也很明显
2. 定时器
了解过窗口函数原理的应该清楚,每一个(key,window)都需要注册两个定时器,而细粒度窗口会导致维护的定时器增多,加重内存负担
一个是触发器注册的定时器,用于决定窗口数据何时输出
第二个是 registerCleanupTimer() 注册的一个清理定时器,用于窗口过期(比如 allowedLateness 过期)之后及时清理窗口的内部状态
这些都是通用的,很多时候其实这些方式解决不了,可以根据实际业务去探索某个业务的最佳方式
另外有时基于海量数据和业务要求的时效性和复杂度经常需要用到算子来处理
相关文章:

FlinkSql通用调优策略
历史文章迁移,稍后整理 使用DataGenerator 提前进行压测,了解数据的处理瓶颈、性能测试和消费能力 开启minibatch:"table.exec.mini-batch.enabled", "true" 开启LocalGlobal 两阶段聚合:"table.exec.m…...

Linux在云计算领域的重要作用
在云计算领域,Linux扮演着至关重要的角色。以下是Linux在云计算领域中的重要作用: 稳定性和安全性:Linux操作系统具有稳定性和安全性,可以有效地保护用户的数据安全。它具有各种安全功能,可以防止未经授权的访问&…...

sqlserver2012 解决日志大的问题 bat脚本
要解决SQL Server 2012中事务日志过大的问题,你可以创建一个批处理脚本(.bat)来定期备份事务日志。下面是一个示例批处理脚本,该脚本使用SQLCMD工具来执行事务日志备份: echo off set "DBNAMEYourDatabaseName&qu…...

SpringCloud之Eureka注册中心和负载均衡
SpringCloud之Eureka注册中心和负载均衡 微服务技术栈认识微服务单体架构分布式架构微服务 微服务拆分及远程调用微服务拆分注意事项 Eureka注册中心提供者与消费者原理分析服务调用出现的问题Eureka的作用 使用流程1、搭建EurekaServer2、注册user-service3、在order-service完…...

Python 数据可视化之山脊线图 Ridgeline Plots
文章目录 一、前言二、主要内容三、总结 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 JoyPy 是一个基于 matplotlib pandas 的单功能 Python 包,它的唯一目的是绘制山脊线图 Joyplots(也称为 Ridgeline Plots&…...
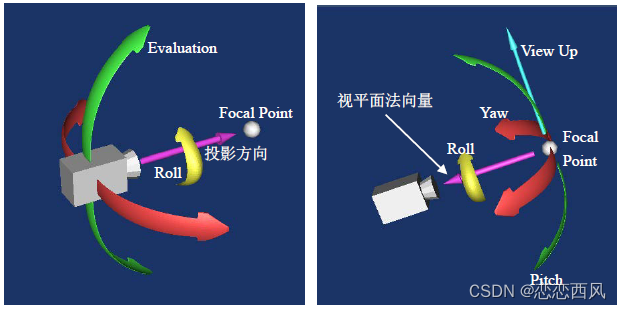
VTK 三维场景的基本要素(相机) vtkCamera 相机的运动
相机的运动 当物体在处于静止位置时,相机可以在物体周围移动,摄取不同角度的图像 移动 移动分为相机的移动,和相机焦点的移动;移动改变了相机相对焦点的位置,离焦点更近或者更远;这样就会改变被渲染的物体…...
。)
C++ //练习 6.53 说明下列每组声明中的第二条语句会产生什么影响,并指出哪些不合法(如果有的话)。
C Primer(第5版) 练习 6.53 练习 6.53 说明下列每组声明中的第二条语句会产生什么影响,并指出哪些不合法(如果有的话)。 (a) int calc(int &, int &);int calc(const int &, const int &); (b) int …...
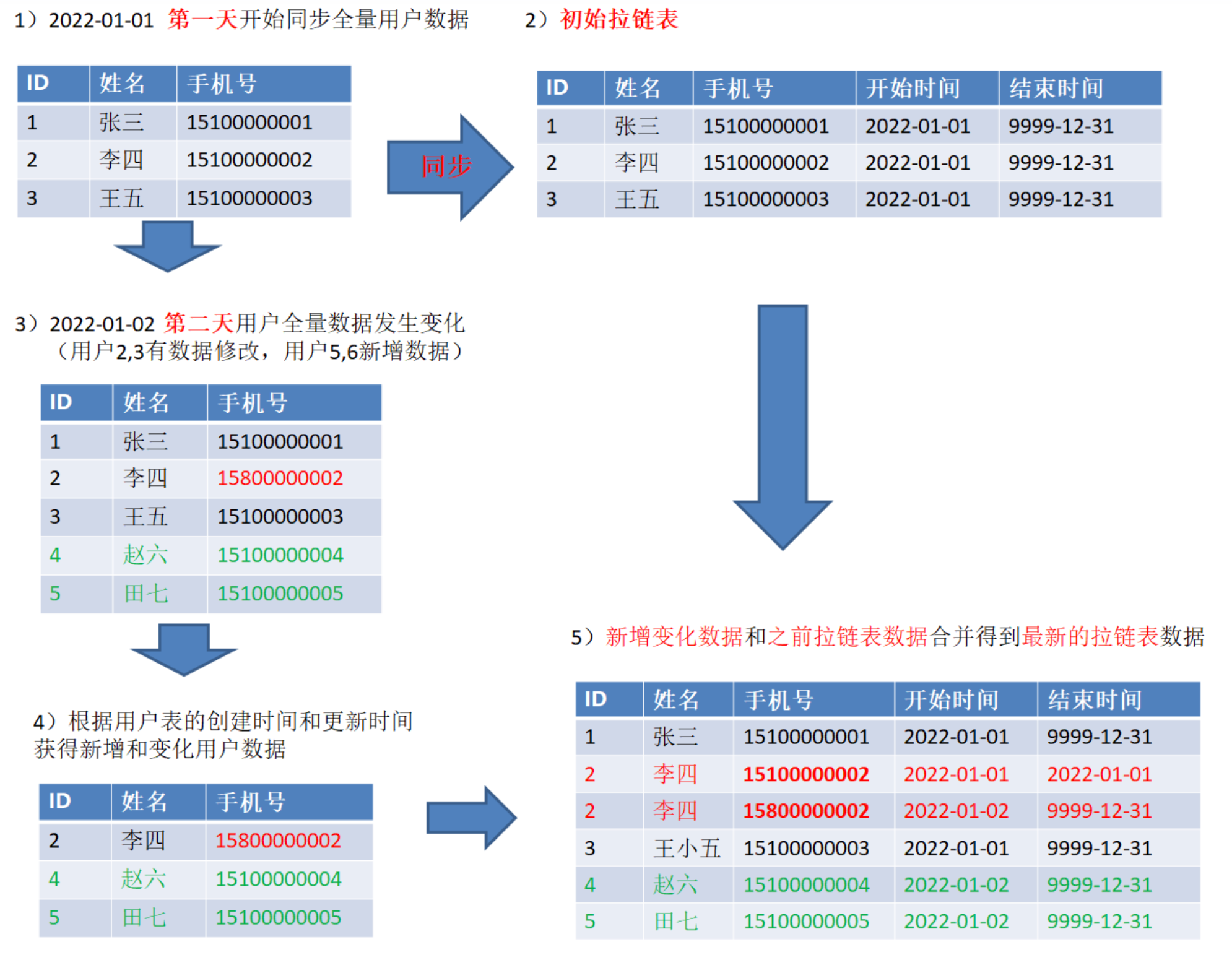
缓慢变化维 常用的处理方法
什么是缓慢变化维 维度 在数仓中,表往往会被划分成两种类型,一种是 事实表,另一种是维度表,举个例子,比如说: ❝ 2024年2月14日,健鑫在12306上买了两张火车票,每张火车票400元&…...
free pascal:fpwebview 组件通过JSBridge调用本机TTS
从 https://github.com/PierceNg/fpwebview 下载 fpwebview-master.zip 简单易用。 先请看 \fpwebview-master\README.md cd \lazarus\projects\fpwebview-master\demo\js_bidir 学习 js_bidir.lpr ,编写 js_bind_speak.lpr 如下,通过JSBridge调用本机…...

C语言静态库深入剖析
在C语言编程实践中,库是代码复用和模块化开发的重要基础结构。静态库作为其中一种主要的库类型,其内容在编译链接阶段即被完整地嵌入到最终生成的可执行文件中,从而使得程序在运行时无需外部依赖。本篇博客将系统性、详细地剖析C语言静态库的…...

A股上市以来涨幅排行榜
一、统计数据说明 1. 涨幅排行榜是根据股价的后复权价格计算的,该价格考虑了分红送股拆股等事件对股价的影响,相当于是分红再投资的股价。 2. 年化投资收益率,是根据IPO收盘价至今涨幅计算的复合年化收益率。例如,假设一个股票上…...
鸿蒙开发系列教程(十八)--页面内动画(1)
页面内的动画 显示动画 语法:animateTo(value: AnimateParam, event: () > void): void 第一个参数指定动画参数 第二个参数为动画的闭包函数。 如:animateTo({ duration: 1000, curve: Curve.EaseInOut }, () > {动画代码}) dura…...
Web基础01-HTML+CSS
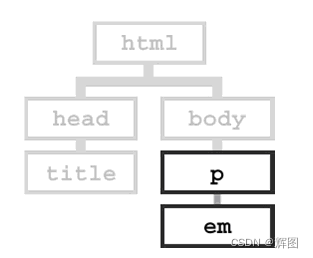
目录 一、HTML 1.概述 2.html结构解析 3.HTML标签分类 4.HTML标签关系 5.HTML空元素 6.HTML属性 7.常用标签 (1)HTML标签 (2)标题标签 (3)换/折行标签 (4)段落标签 &am…...

Linux命令行全景指南:从入门到实践,掌握命令行的力量
目录 知识梳理思维导图: linux命令入门 为什么要学Linux命令 什么是终端 什么是命令 关于Linux命令的语法 tab键补全 关于命令提示符 特殊目录 常见重要目录 /opt /home /root /etc /var/log/ man命令 shutdown命令 history命令 which命令 bash…...

蓝桥杯嵌入式第11届真题(完成) STM32G431
蓝桥杯嵌入式第11届真题(完成) STM32G431 题目 代码 程序和之前的大同小异,不过多解释 main.c /* USER CODE BEGIN Header */ /********************************************************************************* file : main.c* brief :…...

ChatGPT高效提问—prompt实践(教师助手)
ChatGPT高效提问—prompt实践(教师助手) 下面来看看ChatGPT在教育领域有什么用途。 首先设定ChatGPT的角色为高中教师助手。 输入prompt: ChatGPT输出: 教师助手的角色已经设置完成。下面通过几种不同的情景演示如何使用。 1.1.1 制定…...

AI绘画作品的展示和变现-2
4.7 制作红包封面 中国的节日和传统文化元素仍然可以成为创作者们的创作灵感,创造出更多的变现机会。比如元宵节,可以制作大型元宵图案,进行引流并卖出元宵。 而春分、谷雨等节气也可以成为创作的灵感来源,创作出与之相关的图案&…...
Linux---网络套接字
端口号 端口号 端口号是一个2字节16位的整数; 端口号用来标识一个进程, 告诉操作系统, 当前的这个数据要交给哪一个进程来处理; IP地址 端口号能够标识网络上的某一台主机的某一个进程; 一个端口号只能被一个进程占用 在公网上,IP地址能表示唯一的一台主机&…...

前端vue 数字 字符串 丢失精度问题
1.问题 后端返回的数据 是这样的 一个字符串类型的数据 前端要想显示这个 肯定需要使用Json.parse() 转换一下 但是 目前有一个问题 转换的确可以 showId:1206381711026823172 有一个这样的字段 转换了以后 发现 字段成了1206381711026823200 精度直接丢了 原本的数据…...

智能汽车行业产业研究报告:4D成像毫米波雷达—自动驾驶最佳辅助
今天分享的是智能汽车系列深度研究报告:《智能汽车行业产业研究报告:4D成像毫米波雷达—自动驾驶最佳辅助》。 (报告出品方:开源证券) 报告共计:43页 视觉感知最佳辅助——4D 成像毫米波雷达 感知是自动…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
