蓝桥杯每日一题------背包问题(四)
前言
前面讲的都是背包的基础问题,这一节我们进行背包问题的实战,题目来源于一位朋友的询问,其实在这之前很少有题目是我自己独立做的,我一般习惯于先看题解,验证了题解提供的代码是正确的后,再去研究题解,这就给我自己养成了一种依赖的习惯。我害怕自己去挑战没有答案的问题,朋友问的这道题来源于一个小众网站,因此没有题解,出于试一试的态度,我也算比较轻松的做出来了,让我十分有满足感,十分感谢他。但是他好久之前问我的一道题,我现在还没有回他(sorry)。话不多说看题目吧。
数的分解
题目描述
把 A 分解成 B 个各不相同的正整数之和,并且要求每个正整数都不包含数字
2和4,一共有多少种不同的分解方法?注意交换几个整数的顺序被视为同一种方法,例如 1000+1001+18 和 1001+1000+18被视为同一种。
输入描述
第一行包一个整数 T,表示测试数据的规模。接下来 T 行每行 2 个整数A,B。
输出描述
对每个输入输出一个整数表示答案。
输入数据
2
10 2
2019 3
输出数据
2
40785
评测用例规模与约定
对于所有评测用例,1≤T≤10,1≤A≤2500,1≤B≤10。
这道题目类似于蓝桥杯的一道真题,那道真题是分解数字2019,可以去看一下,数的分解。因为那个题目只分解一个数字,所以采用dfs甚至for循环枚举都可以过。但是这道题目是分解好几个数字,而且分解后数字的个数也不是固定的,如果用dfs会超时。
那么试着考虑一下动态规划,因为无法为它划分为区间,状压,期望,树形,所以只能是普通的dp,那就用普通的dp的思考顺序进行思考。
定义dp数组
第一步:缩小规模。 考虑分解成B个整数,那么我用B当作数据规模。
第二步:限制。 需要记录当前B个数字之和是多少。除了这一个限制还有什么限制呢?选出来的数字不能包含2或4,这一个限制好考虑,只需要在选择的时候检查一遍就可以了。还有呢?还有需要保证选择的方案不会重复,这种限制最常见的是用a<b<c来约束,即后一个一定比前一个大,这样相当于规定了选择的顺序,但是如果是这样的话我需要知道前一个选择的是啥,这个时候就需要记录。其它限制应该没有了。
第三步:写出dp数组。 dp[i][j][k]表示当前选择了i个数字,所选数字之和为j且最后一个选择的数字是k时的?。这样要求啥?求方案数啊,一般求啥表示啥(也有特殊情况),所以‘?’表示的是方案数。
第四步:推状态转移方程。 dp[i][j][k]应该从哪里转移过来呢,必然是从前i-1个数字的状态转移,这个状态还应该考虑此时j和k的情况,当前可以选择的数字必然是比j小,比k大,假设当前选择的数字是p,则 k < p < j k<p<j k<p<j。所以 d p [ i ] [ j ] [ p ] + = d p [ i − 1 ] [ j − p ] [ k ] dp[i][j][p] += dp[i-1][j-p][k] dp[i][j][p]+=dp[i−1][j−p][k]
综上状态转移方程如下
d p [ i ] [ j ] [ p ] + = d p [ i − 1 ] [ j − p ] [ k ] dp[i][j][p] += dp[i-1][j-p][k] dp[i][j][p]+=dp[i−1][j−p][k]
考虑写代码了
第一步:确定好遍历顺序。 对于背包问题,一般第一个for遍历规模,第二个for遍历限制。但是我们的限制有两个,所以加上规模一共三层嵌套的for循环。
第二步:确定好转移位置。 对于当前可以选择的数字,只要比k大我都可以尝试在这一步选择,所以需要一个for循环遍历此时转移的数字。综上一共4层嵌套的for循环。那么代码如下
int dp[][][] = new int[k+1][n+1][n+1];//n表示要分解的数字,k表示分解后的数字个数// TODO Auto-generated method stubfor(int i = 1;i <= n;i++) dp[1][i][i] = 1;for(int i = 1;i <= k;i++) {//10 遍历规模for(int j = 1;j <= n;j++) {//2500 遍历限制 for(int q = 1;q <= j;q++) {//if(check(q)) continue;//检查是否包含了2或4for(int p = q+1;p <= j;p++) {if(check(p)) continue;dp[i][j][p] += dp[i-1][j-p][q]; }}}}
可以算一下上述思路的时间复杂度是 O ( k ∗ n ∗ n ∗ n ) = 10 ∗ 2500 ∗ 2500 ∗ 2500 > 1 e 8 O(k*n*n*n)=10*2500*2500*2500>1e8 O(k∗n∗n∗n)=10∗2500∗2500∗2500>1e8,会超时。那么在写上述思路的过程中你有没有发现一个问题。对于n范围内的数字我只有可能会选择一次,选择k个数字,并且数字之和恰好等于n,这像不像二维01背包问题?没错就是!按照刚刚所想重新思考dp数组。
定义dp数组
第一步:缩小规模。 对于n范围内的数字我只有可能会选择一次,小于n的所有数字都可以看作是一个物品,一共有n个物品。
第二步:限制。
限制1:选出来的数字不能包含2或4,这一个限制好考虑,只需要在选择的时候检查一遍就可以了,不需要新的维度。
限制2:选出来的数字个数不能超过B,需要一个维度来限制。
限制3:选出来的数字之和不能超过n,需要一个维度来限制。
第三步:写出dp数组。 dp[i][j][k]表示当前选择了i个数字,所选数字之和为k所选数字个数为j时的方案数。
第四步:推状态转移方程。 dp[i][j][k]应该从哪里转移过来呢,必然是从前i-1个数字的状态转移,如果第i个数字不选,则 dp[i][j][k]+= dp[i-1][j][k],如果选择第i个数字,则 dp[i][j][k]+= dp[i-1][j-1][k-i]
综上状态转移方程如下
i f ( k > i ) if(k>i) if(k>i) d p [ i ] [ j ] [ p ] = d p [ i − 1 ] [ j ] [ k ] + d p [ i − 1 ] [ j − 1 ] [ k − i ] dp[i][j][p] = dp[i-1][j][k]+dp[i-1][j-1][k-i] dp[i][j][p]=dp[i−1][j][k]+dp[i−1][j−1][k−i]
e l s e else else d p [ i ] [ j ] [ p ] = d p [ i − 1 ] [ j ] [ k ] dp[i][j][p] = dp[i-1][j][k] dp[i][j][p]=dp[i−1][j][k]
考虑写代码了
第一步:确定好遍历顺序。 对于背包问题,一般第一个for遍历规模,第二个for遍历限制。但是我们的限制有两个,所以加上规模一共三层嵌套的for循环。
第二步:确定好转移位置。 当前第i个数字进行转移,所以不需要额外的for循环,代码如下
import java.util.Scanner;
import java.util.Set;
import java.util.TreeSet;
public class Main{static int n,k,ans=0;//检查是不是带有2 或 4static Boolean check(int parm) {while(parm>0) {int t=parm%10;if(t==2 || t==4) return true;parm/=10;}return false;}
public static void main(String[] args) {
// f();Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();long dp[][][] = new long[2500+1][10+1][2500+1];//当前考虑的物品,当前选择的物品个数,当前选择的物品的重量,当前物品选还是没选while(t-- > 0) {n=scanner.nextInt();k = scanner.nextInt();int sum=0;//从2500个物品里,选10个物品,且价值恰好为n dp[0][0][0]=1;for(int i = 1;i <= n;i++) {dp[i][1][i] = 1; dp[i][0][0] = 1;
// dp[1][0][0][0] = 1;}for(int i = 1;i <= n;i++) {//for(int j = 1;j <= k;j++) {//for(int q = 1;q <= n;q++) {//if(check(i)) {dp[i][j][q] = dp[i-1][j][q];}else {if(q >= i)dp[i][j][q] = dp[i-1][j-1][q-i]+dp[i-1][j][q];elsedp[i][j][q] = dp[i-1][j][q];}
// System.out.println(dp[i][j][q] + " " + i + " " + j + " " + q);}}}long ans = 0;ans = dp[n][k][n]; System.out.println(ans);}
}
}
此时的时间复杂度是 O ( B ∗ A ∗ A ) = 10 ∗ 2500 ∗ 2500 = 62500000 < 1 e 8 O(B*A*A)=10*2500*2500=62500000<1e8 O(B∗A∗A)=10∗2500∗2500=62500000<1e8,貌似可以,但是别忘了还有T,所以时间复杂度应该是 O ( B ∗ A ∗ A ∗ T ) = 10 ∗ 2500 ∗ 2500 ∗ 10 = 62500000 > 1 e 8 O(B*A*A*T)=10*2500*2500*10=62500000>1e8 O(B∗A∗A∗T)=10∗2500∗2500∗10=62500000>1e8,但是我们可以看到当n=2500,t=1时是不超时的,而对于其它的n<2500和k<=10,其实可以直接用dp[n][k][n]来表示,所以我们只需要预处理出n=2500和k=10的情况,然后针对其它样例直接输出就可以了。
超时的问题解决了,还有一个问题,不太常遇到的问题,空间超限,因为我们设的数组是三维的,空间大小将近1e9了。这里可以考虑用滚动dp来节省空间,滚动dp在背包问题(一)中进行过讲解,修改后的代码如下,
import java.util.Arrays;
import java.util.Scanner;
import java.util.Set;
import java.util.TreeSet;public class Main{static int n,k,ans=0;//检查是不是带有2 或 4static Boolean check(int parm) {while(parm>0) {int t=parm%10;if(t==2 || t==4) return true;parm/=10;}return false;}
public static void main(String[] args) {
// f();Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();long dp[][][] = new long[2][10+1][2500+1];//当前考虑的物品,当前选择的物品个数,当前选择的物品的重量,当前物品选还是没选dp[0][0][0] = 1;dp[1][1][1] = 1;dp[1][0][0] = 1;n = 2500;k = 10;for(int i = 1;i <= n;i++) {//for(int j = 1;j <= k;j++) {//for(int q = 1;q <= n;q++) {// if(check(i)) {dp[i&1][j][q] = dp[(i-1)&1][j][q];}else {if(q >= i)dp[i&1][j][q] = dp[(i-1)&1][j-1][q-i]+dp[(i-1)&1][j][q];elsedp[i&1][j][q] = dp[(i-1)&1][j][q];}
// System.out.println(dp[i][j][q] + " " + i + " " + j + " " + q);}}}while(t-- > 0) {n=scanner.nextInt();k = scanner.nextInt();long ans = 0;ans = dp[n&1][k][n]; System.out.println(ans);}
}
}
这个网站的题目应该是对蓝桥杯题目进行了改编,不得不说改编的质量还是挺高的,再来另一个类似的题目
数的分解2
题目描述
将 N 拆分成 M 个正整数之和,总共有多少种拆分方法?注意交换顺序视为不同的方法,例如 2025 = 1000 + 1025 和 2025 = 1025 + 1000 就视为不同的方法。
输入描述
第一行包一个整数 T,表示测试数据的规模。接下来
T 行每行 2 个整数,N,M。
输出描述
对每个输入输出一个整数表示答案。由于答案可能会很大,请输出答案除以 109+7 的结果。
输入数据
2
40 5
1988 2
输出数据
82251
1987
评测用例规模与约定
对于所有评测用例,1≤T≤10,1≤N≤2500,1≤M≤10。
这道题和上一道题有什么区别呢?除了没有不能选包含2和4的数字的约数之外,还规定了不同的顺序视为不同的方案,这样就不是01背包了。因为对于01背包而言,10+11和11+10是一种方案。还是先按照dp的步骤考虑一下。
定义dp数组
第一步:缩小规模。 考虑分解成B个整数,那么我用B当作数据规模。
第二步:限制。 需要记录当前B个数字之和是多少。
第三步:写出dp数组。 dp[i][j]表示当前选择了i个数字,所选数字之和为j时的方案数。
第四步:推状态转移方程。 dp[i][j]应该从哪里转移过来呢,必然是从前i-1个数字的状态转移,这个状态还应该考虑此时j的情况,当前可以选择的数字必然是比j小,假设当前选择的数字是p,则 p < j p<j p<j。所以 d p [ i ] [ j ] + = d p [ i − 1 ] [ j − p ] dp[i][j] += dp[i-1][j-p] dp[i][j]+=dp[i−1][j−p]
综上状态转移方程如下
d p [ i ] [ j ] [ p ] + = d p [ i − 1 ] [ j − p ] dp[i][j][p] += dp[i-1][j-p] dp[i][j][p]+=dp[i−1][j−p]
考虑写代码了
第一步:确定好遍历顺序。 对于背包问题,一般第一个for遍历规模,第二个for遍历限制。
第二步:确定好转移位置。 对于当前可以选择的数字,只要比j小我都可以尝试在这一步选择,所以需要一个for循环遍历此时转移的数字。综上一共3层嵌套的for循环。那么代码如下
import java.util.Arrays;
import java.util.Scanner;
import java.util.Set;
import java.util.TreeSet;public class Main{static int n,k,ans=0;
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int t = scanner.nextInt();n = 2500;k = 10;int mod = (int) (1e9+7);int dp[][] = new int[k+1][n+1];// TODO Auto-generated method stubfor(int i = 1;i <= n;i++) dp[1][i] = 1;for(int i = 1;i <= k;i++) {//10 遍历规模for(int j = 1;j <= n;j++) {//2500 遍历限制 for(int q = 1;q <= j;q++) {//dp[i][j] += dp[i-1][j-q]; dp[i][j] %= mod;}}}while(t-- > 0) {n=scanner.nextInt();k = scanner.nextInt();long ans = 0;ans = dp[k][n]; System.out.println(ans);}
}
该思路的时间复杂度是 O ( N ∗ M ∗ N ) = 2500 ∗ 2500 ∗ 10 < 1 e 8 O(N*M*N)=2500*2500*10<1e8 O(N∗M∗N)=2500∗2500∗10<1e8,可以通过本题。
可以看见同一个思路,因为限制的降低,dp数组维数降低,时间复杂度就降低了。
相关文章:
)
蓝桥杯每日一题------背包问题(四)
前言 前面讲的都是背包的基础问题,这一节我们进行背包问题的实战,题目来源于一位朋友的询问,其实在这之前很少有题目是我自己独立做的,我一般习惯于先看题解,验证了题解提供的代码是正确的后,再去研究题解…...

OpenAI发布Sora技术报告深度解读!真的太强了!
😎 作者介绍:我是程序员洲洲,一个热爱写作的非著名程序员。CSDN全栈优质领域创作者、华为云博客社区云享专家、阿里云博客社区专家博主、前后端开发、人工智能研究生。公粽号:洲与AI。 🎈 本文专栏:本文收录…...
AJAX——接口文档
1 接口文档 接口文档:描述接口的文章 接口:使用AJAX和服务器通讯时,使用的URL,请求方法,以及参数 传送门:AJAX阶段接口文档 <!DOCTYPE html> <html lang"en"><head><meta c…...

leetcode hot100不同路径
本题可以采用动态规划来解决。还是按照五部曲来做 确定dp数组:dp[i][j]表示走到(i,j)有多少种路径 确定递推公式:我们这里,只有两个移动方向,比如说我移动到(i,j&#x…...

【前端工程化面试题目】webpack 的热更新原理
可以在顺便学习一下 vite 的热更新原理,请参考这篇文章。 首先有几个知识点需要明确 热更新是针对开发过程中的开发服务器的,也就是 webpack-dev-serverwebpack 的热更新不需要额外的插件,但是需要在配置文件中 devServer属性中配置&#x…...
不花一分钱,在 Mac 上跑 Windows(M1/M2 版)
这是在 MacOS M1 上体验最新 Windows11 的效果: VMware Fusion,可以运行 Windows、Linux 系统,个人使用 licence 免费 安装流程见 👉 https://zhuanlan.zhihu.com/p/452412091 从申请 Fusion licence 到下载镜像,再到…...

Attempt to call an undefined function glutInit
Attempt to call an undefined function glutInit 解决方法: 从这里下载PyOpenGL 的whl安装文件, https://drive.google.com/drive/folders/1mz7faVsrp0e6IKCQh8MyZh-BcCqEGPwx 安装命令举栗 pip install PyOpenGL-3.1.7-cp39-cp39-win_amd64.whl pi…...
AB测试最小样本量
1.AB实验过程 常见的AB实验过程,分流-->实验-->数据分析-->决策:分流:用户被随机均匀的分为不同的组实验:同一组内的用户在实验期间使用相同的策略,不同组的用户使用相同或不同的策略。数据收集:…...

在Spring中事务失效的场景
在Spring框架中,事务管理是通过AOP(面向切面编程)实现的,主要依赖于Transactional注解。然而,在某些情况下,事务可能会失效。以下是一些可能导致Spring事务失效的常见场景: 非public方法&#…...

Rust 学习笔记 - 变量声明与使用
前言 任何一门编程语言几乎都脱离不了:变量、基本类型、函数、注释、循环、条件判断,这是一门编程语言的语法基础,只有当掌握这些基础语法及概念才能更好的学习 Rust。 变量介绍 Rust 是一种强类型语言,但在声明变量时…...
windows 下跑起大模型(llama)操作笔记
原贴地址:https://testerhome.com/topics/39091 前言 国内访问 chatgpt 太麻烦了,还是本地自己搭一个比较快,也方便后续修改微调啥的。 之前 llama 刚出来的时候在 mac 上试了下,也在 windows 上用 conda 折腾过,环…...
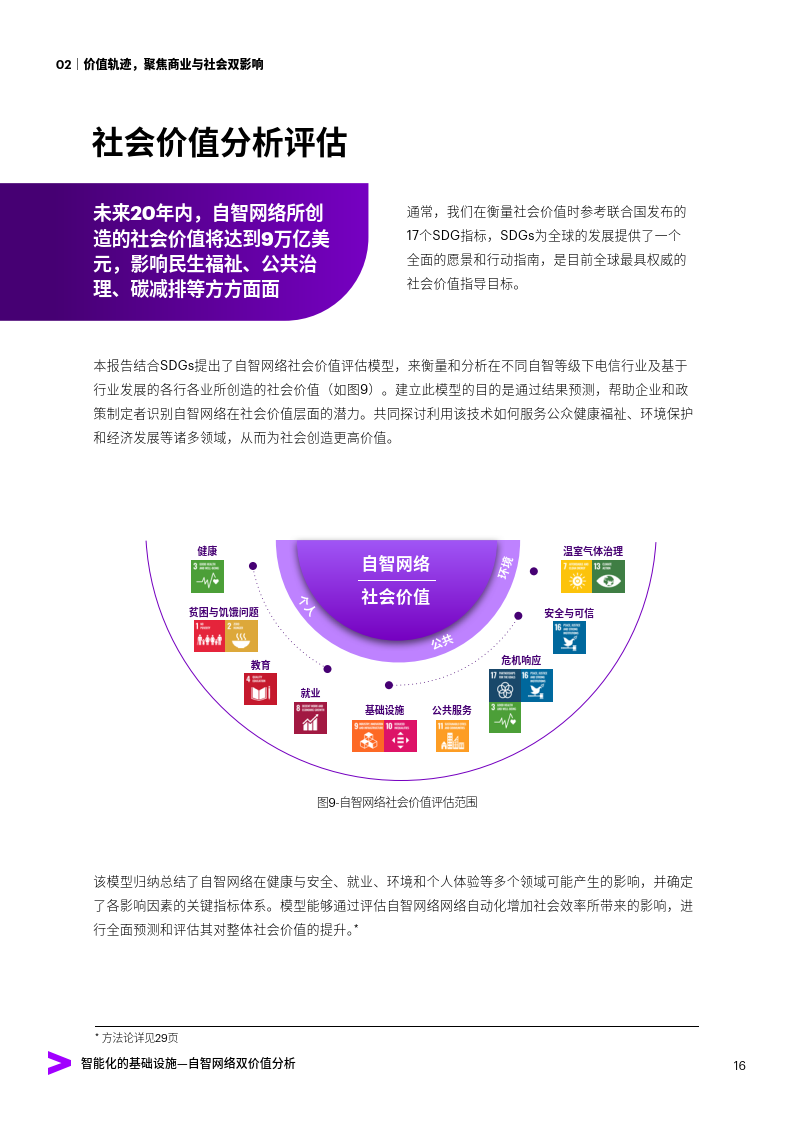
人工智能专题:基础设施行业智能化的基础设施,自智网络双价值分析
今天分享的是人工智能系列深度研究报告:《人工智能专题:基础设施行业智能化的基础设施,自智网络双价值分析》。 (报告出品方:埃森哲) 报告共计:32页 自智网络驱动的电信产业变革 经过多年的…...

docker 编译安装redis脚本
在Docker中编译安装Redis通常不是一个常见的做法,因为Redis官方提供了预编译的Docker镜像,这些镜像包含了已经编译好的Redis二进制文件。不过,如果你有特殊需求,想要自己从源代码编译Redis并打包成Docker镜像,你可以使…...
鸿蒙开发系列教程(二十三)--List 列表操作(2)
列表样式 1、设置内容间距 在列表项之间添加间距,可以使用space参数,主轴方向 List({ space: 10 }) { … } 2、添加分隔线 分隔线用来将界面元素隔开,使单个元素更加容易识别。 startMargin和endMargin属性分别用于设置分隔线距离列表侧…...
C#根据权重抽取随机数
(游戏中一个很常见的简单功能,比如抽卡抽奖抽道具,或者一个怪物有多种攻击动作,按不同的权重随机出个攻击动作等等……) 假如有三种物品 A、B、C,对应的权重分别是A(50),…...

SORA:OpenAI最新文本驱动视频生成大模型技术报告解读
Video generation models as world simulators:作为世界模拟器的视频生成模型 1、概览2、Turning visual data into patches:将视觉数据转换为补丁3、Video compression network:视频压缩网络4、Spacetime Latent Patches:时空潜在…...

阿里云第七代云服务器ECS计算c7、通用g7和内存r7配置如何选择?
阿里云服务器配置怎么选择合适?CPU内存、公网带宽和ECS实例规格怎么选择合适?阿里云服务器网aliyunfuwuqi.com建议根据实际使用场景选择,例如企业网站后台、自建数据库、企业OA、ERP等办公系统、线下IDC直接映射、高性能计算和大游戏并发&…...
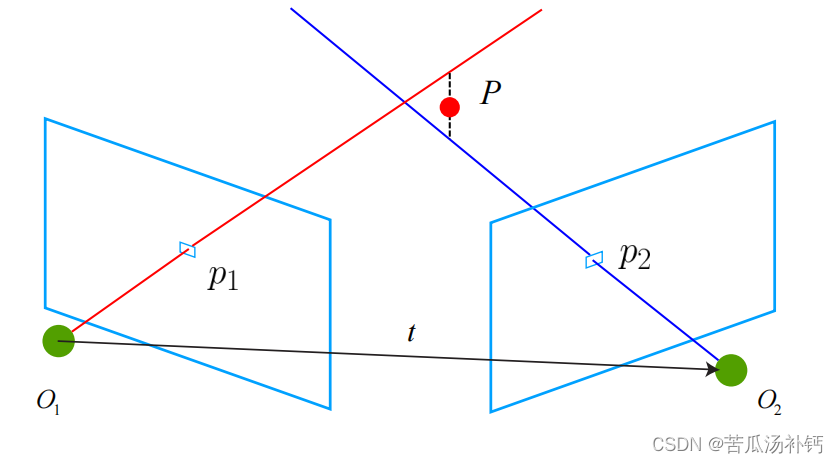
视觉slam十四讲学习笔记(六)视觉里程计 1
本文关注基于特征点方式的视觉里程计算法。将介绍什么是特征点,如何提取和匹配特征点,以及如何根据配对的特征点估计相机运动。 目录 前言 一、特征点法 1 特征点 2 ORB 特征 FAST 关键点 BRIEF 描述子 3 特征匹配 二、实践:特征提取…...
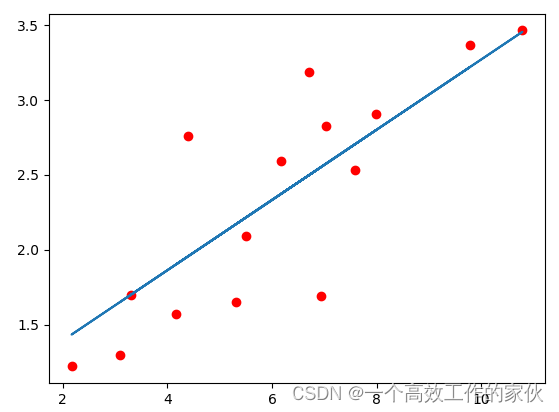
PyTorch-线性回归
已经进入大模微调的时代,但是学习pytorch,对后续学习rasa框架有一定帮助吧。 <!-- 给出一系列的点作为线性回归的数据,使用numpy来存储这些点。 --> x_train np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],[9.779], [6.1…...
C++数据结构与算法——栈与队列
C第二阶段——数据结构和算法,之前学过一点点数据结构,当时是基于Python来学习的,现在基于C查漏补缺,尤其是树的部分。这一部分计划一个月,主要利用代码随想录来学习,刷题使用力扣网站,不定时更…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
