2015-2024年考研数学(一)真题练习和解析——选择题
各个大学已经陆陆续续开学了,备考2025年考研的同学也要紧锣密鼓地开始备考,尤其是三门公共课——政治、英语、数学,备考的时间和周期都比较长,每一门都是难啃的硬骨头。

在这三门公共课中,数学的灵活性是最大的,那么,如何有效提升考研数学的成绩呢?吃透过去的真题是有效的方法之一。通过吃透考研真题,以及题目背后的考点、知识,就能起到举一反三的效果,用更短的时间和成本,让考研数学成绩更上一层楼。
六分成长收集整理了1987-2024年的考研数学一的真题和解析,并把2015-2024年十年的真题做成了在练练习的方式,多种形式的练习,各种终端都可以流畅访问,随时随地用好碎片化时间吃透真题。
今天继续来看5道选择题。
一、2015-2024年考研数学一选择题真题和解析1

解析:

二、2015-2024年考研数学一选择题真题和解析2

解析:

三、2015-2024年考研数学一选择题真题和解析3

解析:

四、2015-2024年考研数学一选择题真题和解析4

解析:

五、2015-2024年考研数学一选择题真题和解析5

解析:

附:考研数学(一)备考资料,更高效、科学地吃透考研数学一真题和知识



相关文章:

2015-2024年考研数学(一)真题练习和解析——选择题
各个大学已经陆陆续续开学了,备考2025年考研的同学也要紧锣密鼓地开始备考,尤其是三门公共课——政治、英语、数学,备考的时间和周期都比较长,每一门都是难啃的硬骨头。 在这三门公共课中,数学的灵活性是最大的&#x…...
Git合并固定分支的某一部分至当前分支
在 Git 中,通常使用 git merge 命令来将一个分支的更改合并到另一个分支。如果你只想合并某个分支的一部分代码,可以使用以下两种方法: 1.批量文件合并 1.1.创建并切换到一个新的临时分支 首先,从要合并的源分支(即要…...
 (A-E))
Codeforces Round 928 (Div. 4) (A-E)
比赛地址 : https://codeforces.com/contest/1926 A 遍历每一个字符串,比较1和0的数量即可,那个大输出那个; #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \n #define lowbit(x) (x&am…...

git远程操控gitee
配置SSH公钥 首先,在本地计算机上生成SSH公钥。打开终端或命令提示符窗口,并执行以下命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com"按照提示操作,生成SSH密钥对。默认情况下,公钥将保存在~…...
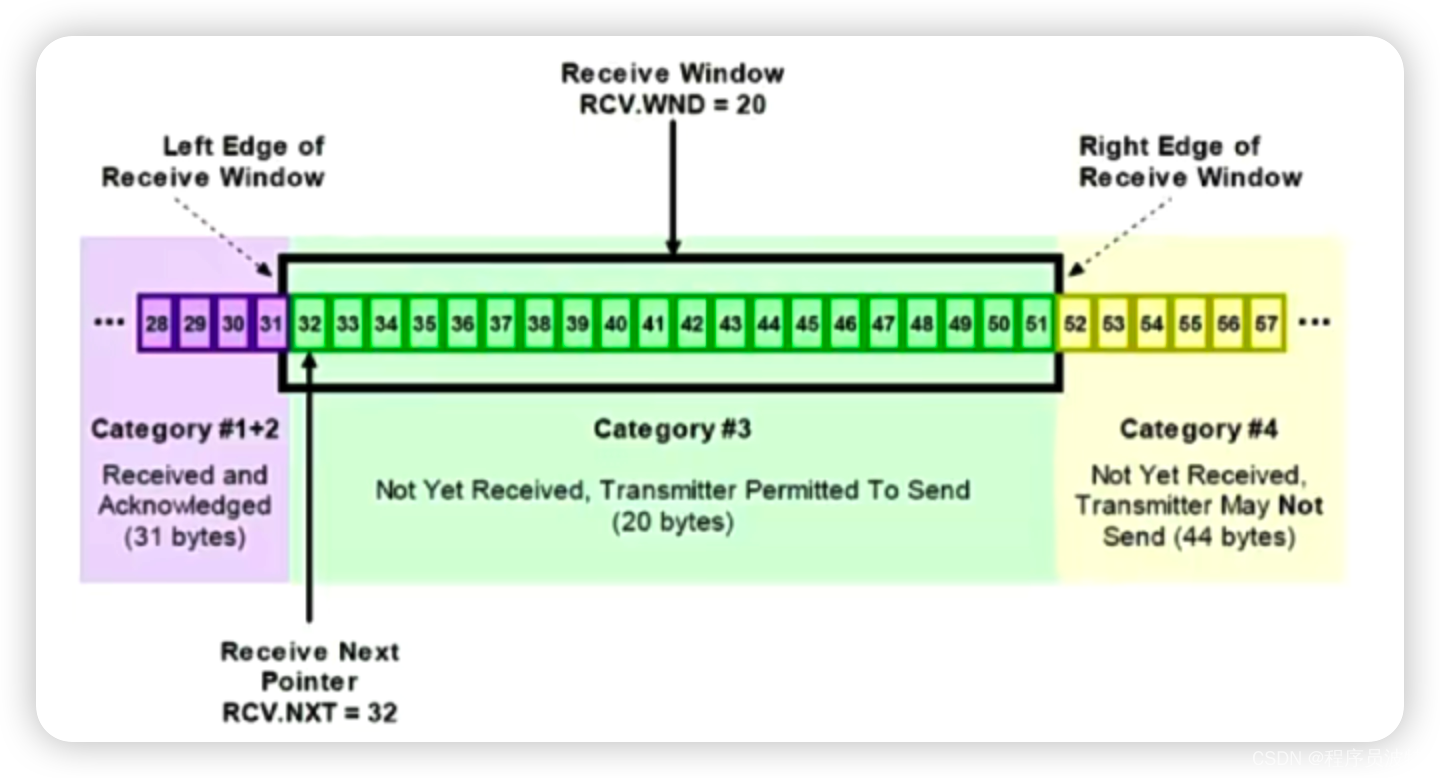
常见面试题:TCP的四次挥手和TCP的滑动窗口
说一说 TCP 的四次挥手。 挥手即终止 TCP 连接,所谓的四次挥手就是指断开一个 TCP 连接时。需要客户端和服务端总共发出四个包,已确认连接的断开在 socket 编程中,这一过程由客户端或服务端任意一方执行 close 来触发。这里我们假设由客户端…...

力扣随笔之两数之和 Ⅱ -输入有序数组(中等167)
思路:在递增数组中找出满足相加之和等于目标数 定义左右两个指针(下标)从数组两边开始遍历,若左右指针所指数字之和大于目标数,则将右指针自减,若左右指针所指数字之和小于目标数,则左指针自加&…...
最优传输(Optimal Transport)
最优传输(Optimal Transport)是一种数学理论和计算方法,用于描述两个概率分布之间的距离或者对应关系。它的核心概念是如何以最佳方式将一组资源(如质量、能量等)从一个位置传输到另一个位置。 基本概念: …...
MIT-6.824-Lab2,Raft部分笔记|Use Go
文章目录 前记Paper6:RaftLEC5、6:RaftLAB22AtaskHintlockingstructureguide设计与编码 2BtaskHint设计与编码 2CtaskHint question后记 LEC5:GO, Threads, and Raftgo threads技巧raft实验易错点debug技巧 前记 趁着研一考完期末有点点空余…...
使用openeuler 22.03替代CentOS 7.9,建立虚拟机详细步骤
进入浏览器搜索网址下载openeuler 22.03镜像文件 https://mirrors.huaweicloud.com/openeuler/openEuler-22.03-LTS-SP3/ISO/x86_64/openEuler-22.03-LTS-SP3-x86_64-dvd.iso 打开VMware Workstation新建一个虚拟机: 自定义虚拟机位置 加入下载好的openeuler镜像文件…...

代理技术引领出海征程
在数字娱乐的繁荣时代,游戏开发者和发行商们意识到,要在全球市场立足,必须迈向国际化的出海之路。然而,这一旅程面临着跨越网络壁垒、适应多元文化和提升全球连接性的巨大挑战。本文将深入探讨代理技术在游戏行业出海过程中的创新…...
谷粒商城篇章9 ---- P248-P261/P292-P294 ---- 消息队列【分布式高级篇六】
目录 1 消息队列(Message Queue)简介 1.1 概述 1.2 消息服务中两个重要概念 1.3 消息队列主要有两种形式的目的地 1.4 JMS和AMQP对比 1.5 应用场景 1.6 Spring支持 1.7 SpringBoot自动配置 1.7 市面上的MQ产品 2 RabbitMQ 2.1 RabbitMQ简介 2.1.1 RabbitMQ简介 2…...
----生命周期事件)
【Spring连载】使用Spring Data访问 MongoDB(五)----生命周期事件
【Spring连载】使用Spring Data访问 MongoDB(五)----生命周期事件Lifecycle Events 一、实体回调Entity Callbacks1.1 实现实体回调1.2 注册实体回调 二、特定存储的实体回调 一、实体回调Entity Callbacks 1.1 实现实体回调 1.2 注册实体回调 二、特…...

JavaSec 之 SQL 注入简单了解
文章目录 JDBC 注入语句拼接(Statement)修复方案 语句拼接(PrepareStatement)修复方案 预编译 JdbcTemplate修复方案 MyBatisLike 注入Order By 注入In 注入 寒假学了一个月 pwn,真心感觉这玩意太底层学的我生理不适应了,接下来学一段时间 java 安全缓一…...

第十一章——期约与异步函数
ECMAScript 6及之后的几个版本逐步加大了对异步编程机制的支持,提供了令人眼前一亮的新特性。ECMAScript 6新增了正式的Promise(期约)引用类型,支持优雅地定义和组织异步逻辑。接下来几个版本增加了使用async和await关键字定义异步…...

工具方法合集-utils.js
通用 import get from lodash.get import cloneDeep from lodash.clonedeep // 深度clone export function deepClone(obj) {return obj ? cloneDeep(obj) : obj } export function lodashGet(obj, key, defaultValue = ) {//这个 defaultValue 不能给默认 值 会报错;retur…...

安卓11-设置HDMI分辨率流程
安卓11中从设置-显示设置hdmi分辨率流程:framework层通过jni控制底层驱动实现,标准驱动模型 packages\apps\Settings\src\com\android\settings\display\HdmiSettings.javaprivate void updateResolution(final ITEM_CONTROL control, final int index) {showWaitin…...
Vue3+vite搭建基础架构(11)--- 菜单栏功能和Tab页功能实现
Vue3vite搭建基础架构(11)--- 菜单栏功能和Tab页功能实现 说明删除项目中不需要的文件userStore全局属性代码菜单栏代码Tab页代码解决浏览器输入地址时不会打开tab页问题和切换tab页时参数丢失问题 说明 这里记录下自己在Vue3vite的项目实现菜单栏功能和…...

餐饮神秘顾客公司:关于餐饮行业神秘顾客调查注意事项
在餐饮业,顾客体验往往决定品牌的成败。为深入了解顾客需求和感受,许多餐饮企业引入“神秘顾客”调查。然而,此调查并非简单走过场,其中细节和注意事项颇多。餐饮行业神秘顾客调查需注意以下几点: 1. 专业培训&#x…...
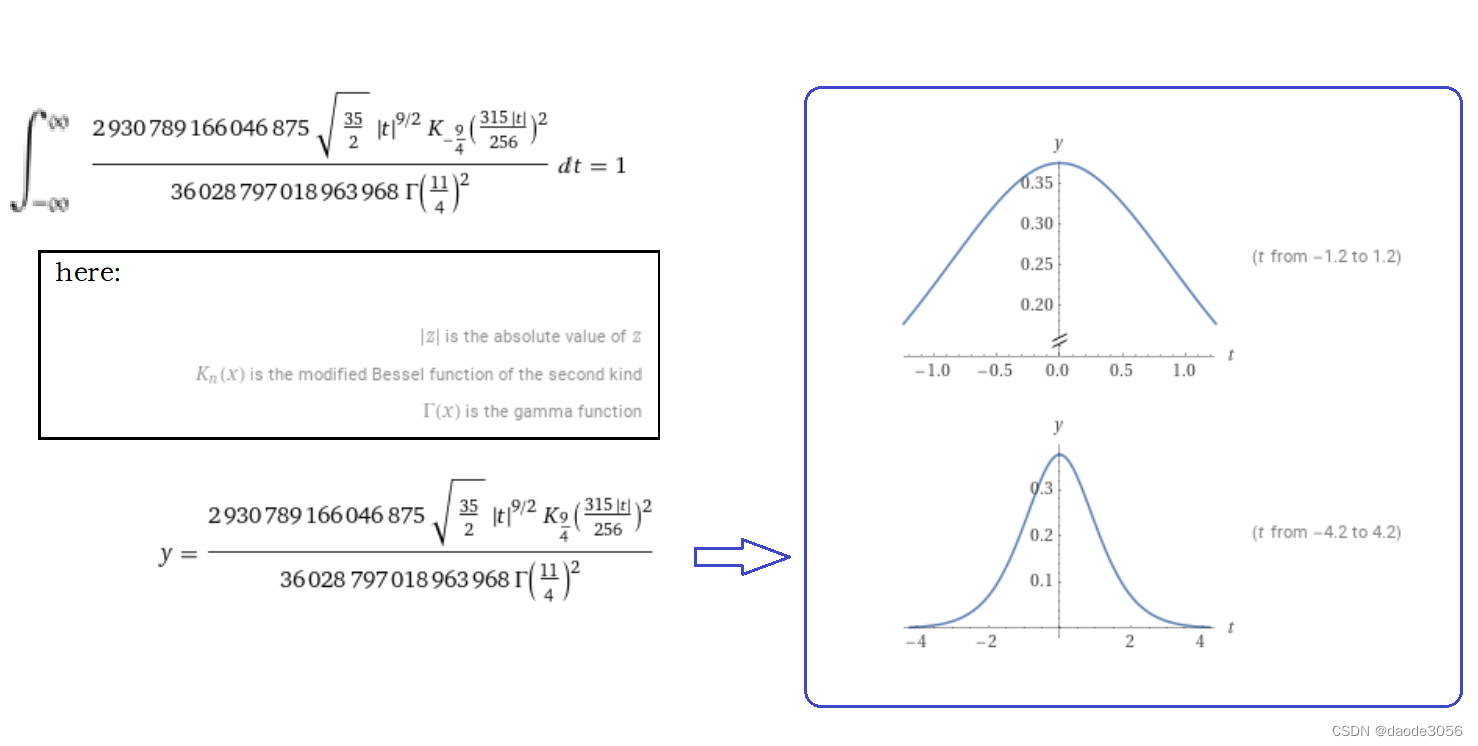
概率密度函数(PDF)与神经网络中的激活函数
原创:项道德(daode3056,daode1212) 在量子力学中,许多现象都是统计的结果,基本上用的是正态分布,然而,从本质上思考,应该还存在低阶的分布,标准的正态分布是它的极限,这样一来,或许在…...
.netcore 6.0/7.0项目迁移至.netcore 8.0 注意事项
1、SqlSugarCore 相关 1.1 主项目添加数据,否则会报数据库连接错误: <InvariantGlobalization>false</InvariantGlobalization> <PropertyGroup><TargetFramework>net8.0</TargetFramework><Nullable>enable</…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
