2-18算法习题总结
二分查找问题
[COCI 2011/2012 #5] EKO / 砍树
题目描述
伐木工人 Mirko 需要砍 M M M 米长的木材。对 Mirko 来说这是很简单的工作,因为他有一个漂亮的新伐木机,可以如野火一般砍伐森林。不过,Mirko 只被允许砍伐一排树。
Mirko 的伐木机工作流程如下:Mirko 设置一个高度参数 H H H(米),伐木机升起一个巨大的锯片到高度 H H H,并锯掉所有树比 H H H 高的部分(当然,树木不高于 H H H 米的部分保持不变)。Mirko 就得到树木被锯下的部分。例如,如果一排树的高度分别为 20 , 15 , 10 20,15,10 20,15,10 和 17 17 17,Mirko 把锯片升到 15 15 15 米的高度,切割后树木剩下的高度将是 15 , 15 , 10 15,15,10 15,15,10 和 15 15 15,而 Mirko 将从第 1 1 1 棵树得到 5 5 5 米,从第 4 4 4 棵树得到 2 2 2 米,共得到 7 7 7 米木材。
Mirko 非常关注生态保护,所以他不会砍掉过多的木材。这也是他尽可能高地设定伐木机锯片的原因。请帮助 Mirko 找到伐木机锯片的最大的整数高度 H H H,使得他能得到的木材至少为 M M M 米。换句话说,如果再升高 1 1 1 米,他将得不到 M M M 米木材。
输入格式
第 1 1 1 行 2 2 2 个整数 N N N 和 M M M, N N N 表示树木的数量, M M M 表示需要的木材总长度。
第 2 2 2 行 N N N 个整数表示每棵树的高度。
输出格式
1 1 1 个整数,表示锯片的最高高度。
样例 #1
样例输入 #1
4 7
20 15 10 17
样例输出 #1
15
样例 #2
样例输入 #2
5 20
4 42 40 26 46
样例输出 #2
36
提示
对于 100 % 100\% 100% 的测试数据, 1 ≤ N ≤ 1 0 6 1\le N\le10^6 1≤N≤106, 1 ≤ M ≤ 2 × 1 0 9 1\le M\le2\times10^9 1≤M≤2×109,树的高度 ≤ 4 × 1 0 5 \le 4\times 10^5 ≤4×105,所有树的高度总和 > M >M >M。
这道题我还没写出来
动态规划问题
疯狂的采药
题目背景
此题为纪念 LiYuxiang 而生。
题目描述
LiYuxiang 是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同种类的草药,采每一种都需要一些时间,每一种也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是 LiYuxiang,你能完成这个任务吗?
此题和原题的不同点:
1 1 1. 每种草药可以无限制地疯狂采摘。
2 2 2. 药的种类眼花缭乱,采药时间好长好长啊!师傅等得菊花都谢了!
输入格式
输入第一行有两个整数,分别代表总共能够用来采药的时间 t t t 和代表山洞里的草药的数目 m m m。
第 2 2 2 到第 ( m + 1 ) (m + 1) (m+1) 行,每行两个整数,第 ( i + 1 ) (i + 1) (i+1) 行的整数 a i , b i a_i, b_i ai,bi 分别表示采摘第 i i i 种草药的时间和该草药的价值。
输出格式
输出一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
样例 #1
样例输入 #1
70 3
71 100
69 1
1 2
样例输出 #1
140
提示
数据规模与约定
- 对于 30 % 30\% 30% 的数据,保证 m ≤ 1 0 3 m \le 10^3 m≤103 。
- 对于 100 % 100\% 100% 的数据,保证 1 ≤ m ≤ 1 0 4 1 \leq m \le 10^4 1≤m≤104, 1 ≤ t ≤ 1 0 7 1 \leq t \leq 10^7 1≤t≤107,且 1 ≤ m × t ≤ 1 0 7 1 \leq m \times t \leq 10^7 1≤m×t≤107, 1 ≤ a i , b i ≤ 1 0 4 1 \leq a_i, b_i \leq 10^4 1≤ai,bi≤104。
最后一个测试点没过
代码如下:
package exercise.luogu.dp;import java.util.Scanner;public class P1616 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int t = sc.nextInt();int n = sc.nextInt();int[] val = new int[n];int[] time = new int[n];int dp[] = new int[t + 1];for (int i = 0; i < n; i++) {time[i] = sc.nextInt();val[i] = sc.nextInt();}// 完全背包问题:每种药材都可以采多次for (int i = 0; i < n; i++) { // 遍历每种药材for (int j = time[i]; j <= t; j++) { // 遍历背包容量,注意从time[i]开始// 当前药材可以放入背包中,比较放入与不放入哪种情况价值更高dp[j] = Math.max(dp[j], dp[j - time[i]] + val[i]);}}System.out.println(dp[t]);}
}总结:
我感觉完全背包问题比部分背包问题要简单得多!
贪心问题
删数问题
题目描述
键盘输入一个高精度的正整数 N N N(不超过 250 250 250 位),去掉其中任意 k k k 个数字后剩下的数字按原左右次序将组成一个新的非负整数。编程对给定的 N N N 和 k k k,寻找一种方案使得剩下的数字组成的新数最小。
输入格式
输入两行正整数。
第一行输入一个高精度的正整数 n n n。
第二行输入一个正整数 k k k,表示需要删除的数字个数。
输出格式
输出一个整数,最后剩下的最小数。
样例 #1
样例输入 #1
175438
4
样例输出 #1
13
代码如下:
package exercise.luogu.greedy;import java.util.Scanner;
import java.util.Stack;public class P1106 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);String str = sc.next();int k = sc.nextInt();char[] charArray = str.toCharArray();Stack<Character> stack = new Stack<>();int removeCount = 0;for (int i = 0; i < charArray.length; i++) {//如果栈顶元素大于当前元素,pop出栈顶元素,把当前元素加入栈while (!stack.isEmpty() && stack.peek() > charArray[i] && removeCount < k) {stack.pop();removeCount++;}stack.push(charArray[i]);}// 如果还有需要删除的数字,则从栈顶开始删除while (removeCount < k) {stack.pop();removeCount++;}// 将栈中的数字转换为字符串并输出StringBuilder sb = new StringBuilder();while (!stack.isEmpty()) {sb.append(stack.pop());}sb.reverse(); // 因为栈是后进先出的,所以需要反转字符串才能得到正确的结果System.out.println(Integer.parseInt(sb.toString()));}
}
分支问题
【模板】快速幂
题目描述
给你三个整数 a , b , p a,b,p a,b,p,求 a b m o d p a^b \bmod p abmodp。
输入格式
输入只有一行三个整数,分别代表 a , b , p a,b,p a,b,p。
输出格式
输出一行一个字符串 a^b mod p=s,其中 a , b , p a,b,p a,b,p 分别为题目给定的值, s s s 为运算结果。
样例 #1
样例输入 #1
2 10 9
样例输出 #1
2^10 mod 9=7
提示
样例解释
2 10 = 1024 2^{10} = 1024 210=1024, 1024 m o d 9 = 7 1024 \bmod 9 = 7 1024mod9=7。
数据规模与约定
对于 100 % 100\% 100% 的数据,保证 0 ≤ a , b < 2 31 0\le a,b < 2^{31} 0≤a,b<231, a + b > 0 a+b>0 a+b>0, 2 ≤ p < 2 31 2 \leq p \lt 2^{31} 2≤p<231。
代码如下:
package exercise.luogu.fenzhi;import java.util.Scanner;public class P1226 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int a = sc.nextInt();int b = sc.nextInt();int p = sc.nextInt();int s = fastPowMod(a, b, p);System.out.printf("%d^%d mod %d=%d", a, b, p, s);}//快速幂算法private static int fastPowMod(int a, int b, int p) {if (b == 0) {return 1;}int halfMod = fastPowMod(a, b / 2, p);int modSquare = (int) (((long) halfMod * halfMod) % p);//如果 b 是偶数,那么 a^b = (a^(b/2))^2。if (b % 2 == 0) {return modSquare;} else {//如果 b 是奇数,那么 a^b = a * (a^(b-1))。//我们首先计算 a^((b-1)/2) mod p(这仍然是 halfMod,因为整数除法会向下取整)return (int) (((long) modSquare * a) % p);}}
}相关文章:

2-18算法习题总结
二分查找问题 [COCI 2011/2012 #5] EKO / 砍树 题目描述 伐木工人 Mirko 需要砍 M M M 米长的木材。对 Mirko 来说这是很简单的工作,因为他有一个漂亮的新伐木机,可以如野火一般砍伐森林。不过,Mirko 只被允许砍伐一排树。 Mirko 的伐木…...

【软考高项】【英语知识】-- 单词积累
目录 一、常见计算机技术词汇 二、项目管理词汇 2.1 十大知识域 2.2 五大过程组 2.3 49个子过程 2.4 工具和技术汇总 2.5 输入和输出汇总 一、常见计算机技术词汇 序号中文英文1云计算Cloud computing2云存储Cloud storage3云服务Cloud service4软件即服务SaaS5平台即服…...
外包干了3个月,技术退步明显
先说一下自己的情况,本科生,19年通过校招进入广州某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...

【ArcGIS微课1000例】0105:三维模型转体模型(导入sketchup转多面体为例)
文章目录 一、实验概述二、三维模型转多面体三、加载多面体数据四、注意事项一、实验概述 ArcGIS可以借助【导入3D文件】工具支持主流的三维模型导入。支持 3D Studio Max (.3ds)、VRML and GeoVRML 2.0 (.wrl)、SketchUp 6.0 (.skp)、OpenFlight 15.8 (.flt)、Collaborative …...
创建型设计模式 - 原型设计模式 - JAVA
原型设计模式 一 .简介二. 案例三. 补充知识 前言 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神的孩子都在歌唱 一 .简介 原型模式提供了一种机制,可以将原始对象复制到新对象࿰…...

Squid代理:APT、PyPI和Docker的内网穿透解决方案
如果你是在内网环境,并且你知道一台服务器可以链接外网,可以通过Squid代理的方式更新apt、pypi、docker源。 你可以通过在服务器A(172.16.16.122,可上外网)上设置代理服务器来实现服务器B通过服务器A访问外部APT源的需…...

MYSQL--触发器
一:介绍: 1.触发器实际上就是一种特殊的存储过程,两者都能够在MYSQL当中完成特定的功能,存储在服务器上的特殊SQL片段,可以重复进行使用,提高复用性的一种功能.但是触发器并不需要进行调用,在使用DML操作的时候会自动的调用相关的触发器操作 2.触发器能够对于DML操作当中的,删除…...

onnx 1.16 doc学习笔记四:python API-If和Scan
onnx作为一个通用格式,很少有中文教程,因此开一篇文章对onnx 1.16文档进行翻译与进一步解释, onnx 1.16官方文档:https://onnx.ai/onnx/intro/index.html](https://onnx.ai/onnx/intro/index.html), 如果觉得有收获&am…...

如何构建企业专属GPT
大语言模型(LLM)具有令人印象深刻的自然语言理解和生成能力, 2022年11月底OpenAI发布了ChatGPT,一跃成为人工智能AI领域的现象级应用。但由于LLM的训练数据集主要来源于互联网数据,企业私域信息并未被LLM所训练&#x…...

知识积累(二):损失函数正则化与权重衰减
文章目录 1. 欧氏距离与L2范数1.1 常用的相似性度量 2. 什么是正则化?参考资料 本文只介绍 L2 正则化。 1. 欧氏距离与L2范数 欧氏距离也就是L2范数 1.1 常用的相似性度量 1)点积 2)余弦相似度 3)L1和L2 2. 什么是正则化&…...
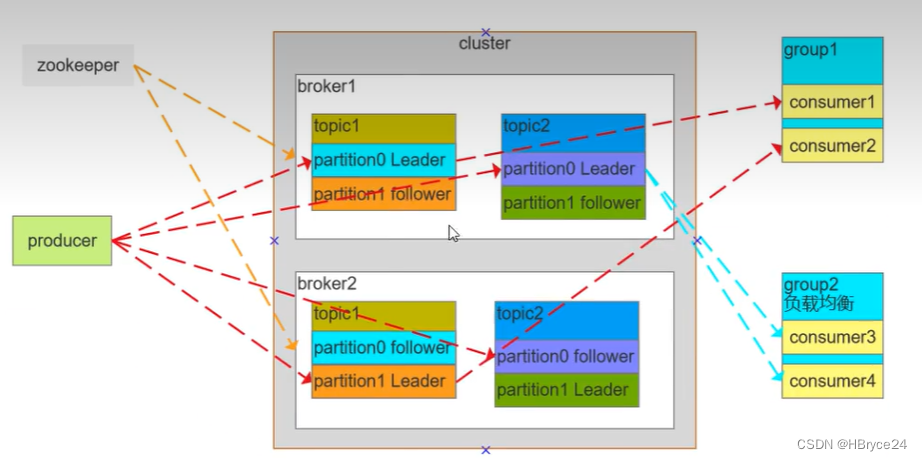
消息中间件-面试题
MQ选择 一、Kafka 1、消息队列如何保证消息可靠性 消息不重复 生产者控制消费者幂等消息不丢失 生产者发送,要确认broker收到并持久化broker确认消费者消费完,再删除消息2、kafka是什么 Kafka是一种高吞吐量、分布式、基于发布/订阅的消息中间件,是Apache的开源项目。broke…...

Python 将二维数组或矩阵变为三维
Python 将二维数组或矩阵变为三维 引言正文基础 拓展 引言 之前,我们已经介绍过了 Python 将一维数组或矩阵变为三维。然而,很多时候,我们也需要对二维矩阵进行操作,这里特来介绍一下如何将二维矩阵扩展为三维。 阅读这一篇前推…...

区块链与Solidity详细介绍及基本语法使用
一、区块链简介 区块链是一种分布式数据库技术,它以块的形式存储数据,并通过加密算法确保数据的安全性。每个块包含一系列交易,并通过哈希值与前一个块相连接,形成一个链式结构。这种结构使得数据难以被篡改,因为任何对…...

题目 1253: 老王赛马
题目描述: 赛马是一古老的游戏,早在公元前四世纪的中国,处在诸侯割据的状态,历史上称为“战国时期”。在魏国作官的孙膑,因为受到同僚庞涓的迫害,被齐国使臣救出后,到达齐国国都。 赛马是当时最受齐国贵族…...
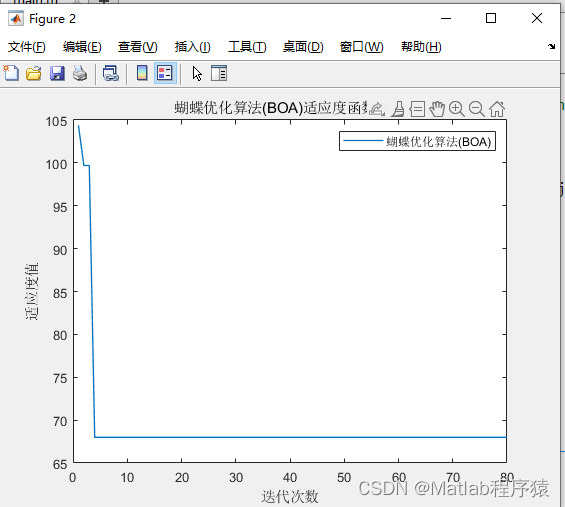
【MATLAB源码-第144期】基于matlab的蝴蝶优化算法(BOA)无人机三维路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 蝴蝶优化算法(Butterfly Optimization Algorithm, BOA)是基于蝴蝶觅食行为的一种新颖的群体智能算法。它通过模拟蝴蝶个体在寻找食物过程中的嗅觉导向行为以及随机飞行行为,来探索解空间…...
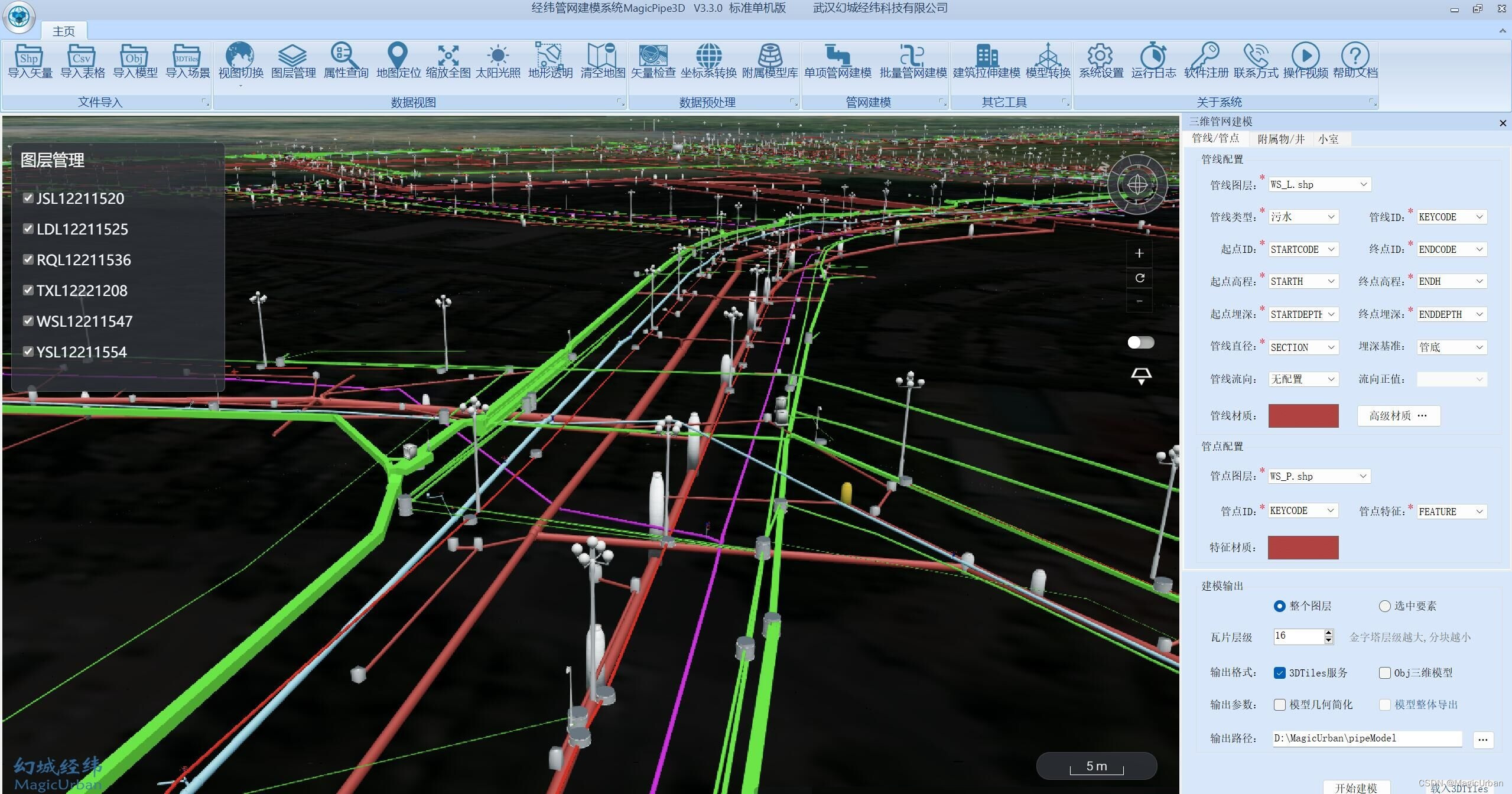
地下管线管网三维建模工具MagicPipe3D V3.4.2发布
经纬管网建模系统MagicPipe3D,本地离线参数化构建地下管网三维模型(包括管道、接头、附属设施等),输出标准3DTiles服务、Obj模型等格式,支持Cesium、Unreal、Unity、Osg等引擎加载进行三维可视化、语义查询、专题分析&…...
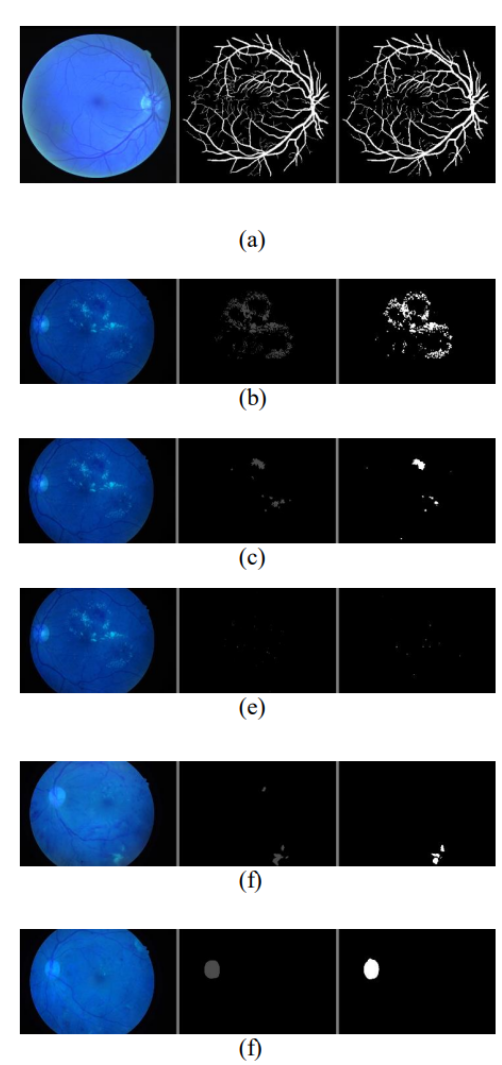
糖尿病性视网膜病变(DR)的自动化检测和分期
糖尿病性视网膜病变(DR)的自动化检测和分期 提出背景DR的阶段及其特征 历年解法计算机视觉方法多分类方法 新的解法深度学习方法迁移学习大模型多模型集成全流程分析 总结特征1:图像分割特征2:疾病分级特征3:治疗建议生…...
C 标准库 - <errno.h>
在C语言编程中,<errno.h> 头文件扮演着至关重要的角色,它提供了一个全局变量 errno 以及一系列预定义宏,用于指示系统调用或库函数执行过程中发生的错误。这些宏有助于程序员诊断和处理运行时错误。 errno 变量 extern int errno;err…...
基于springboot+vue的房屋租赁管理系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...
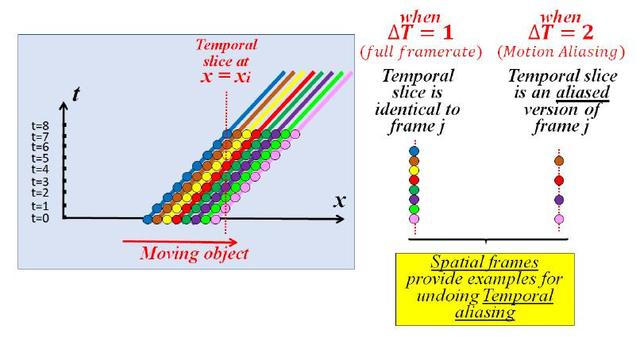
Sora----打破虚实之间的最后一根枷锁----这扇门的背后是人类文明的晟阳还是最后的余晖
目录 一.Sora出道即巅峰 二.为何说Sora是该领域的巨头 三.Sora无敌的背后究竟有怎样先进的处理技术 1.Spacetime Latent Patches 潜变量时空碎片,建构视觉语言系统 2.扩散模型与Diffusion Transformer,组合成强大的信息提取器 3.DiT应用于潜变量时…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
