【数据结构初阶 6】二叉树:堆的基本操作 + 堆排序的实现
文章目录
- 🌈 Ⅰ 二叉树的顺序结构
- 🌈 Ⅱ 堆的概念与性质
- 🌈 Ⅲ 堆的基本操作
- 01. 堆的定义
- 02. 初始化堆
- 03. 堆的销毁
- 04. 堆的插入
- 05. 向上调整堆
- 06. 堆的创建
- 07. 获取堆顶数据
- 08. 堆的删除
- 09. 向下调整堆
- 10. 判断堆空
- 🌈 Ⅳ 堆的基本应用
- 01. 堆排序的实现
- 02. TOP K 问题
🌈 Ⅰ 二叉树的顺序结构
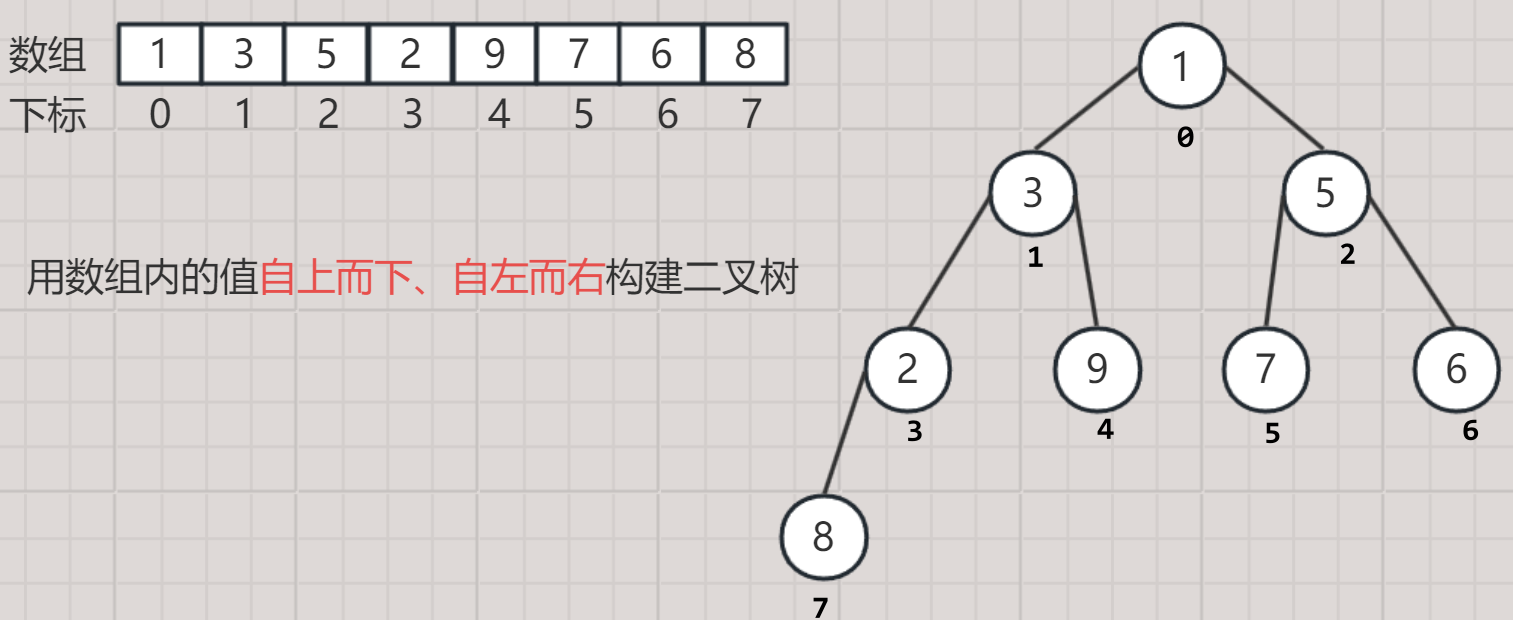
1. 顺序存储结构概念
- 顺序存储结构就是使用数组来存储二叉树的数据。
- 这种结构下的逻辑结构是二叉树,物理结构是数组。
- 数组内的值是将二叉树自上而下、自左而右依次存储,反过来数组构建二叉树也是这个顺序。
2. 顺序存储结构优势
使用这种结构可以很容易得出父子结点的下标。
- 双亲结点下标 = ( 左或右孩子结点下标 - 1 ) / 2
- 左孩子结点下标 = 双亲结点下标 * 2 + 1
- 右孩子结点下标 = 双亲结点下标 * 2 + 2
3. 适合顺序存储的二叉树
- 只有满二叉树或完全二叉树这种能够有效利用数组空间,适合使用顺序存储。
🌈 Ⅱ 堆的概念与性质
1. 堆的概念
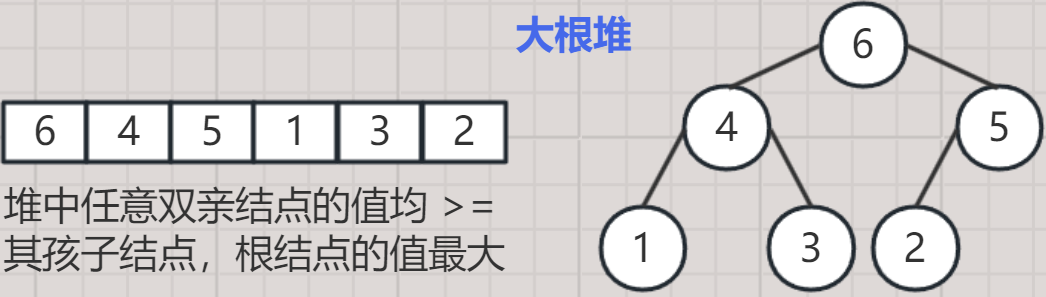
- 将一组数据构建成一棵完全二叉树,如果根节点的值 大于 / 小于 左右子树的所有值,则称该完全二叉树为一个堆。
- 将根节点最大的堆称做大根堆;将根节点最小的堆称为小根堆。
2. 堆的性质
- 堆总是一棵完全二叉树。
- 有序数组一定是堆,反之却不一定。
- 小根堆:堆中所有双亲结点的值总是 <= 其孩子结点,根结点的值最小。
- 大根堆:堆中所有双亲结点的值总是 >= 其孩子结点,根结点的值最大。
🌈 Ⅲ 堆的基本操作
01. 堆的定义
- 堆在计算机看来实际就是个数组,但不能只用数组表示堆,还需要记录下每个堆的有效数据个数以及对应堆的容量。
- 因此就要建立一个堆的结构体来管理每个堆。
typedef int HPDataType; // 堆中每个结点的数据类型typedef struct Heap
{int size; // 记录数组中有效数据个数int capacity; // 记录开辟的数组空间大小HPDataType* data; // 为堆空间开辟的数组
}Heap;
- 注意:因为 size 是用来记录堆中有效数据的个数,因此 size 天生是最后一个有效数据的后一个位置的下标。
02. 初始化堆
void HeapInit(Heap* hp)
{assert(hp);hp->data = NULL;hp->size = hp->capacity = 0;
}
03. 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->data);hp->data = NULL;hp->size = hp->capacity = 0;
}
04. 堆的插入
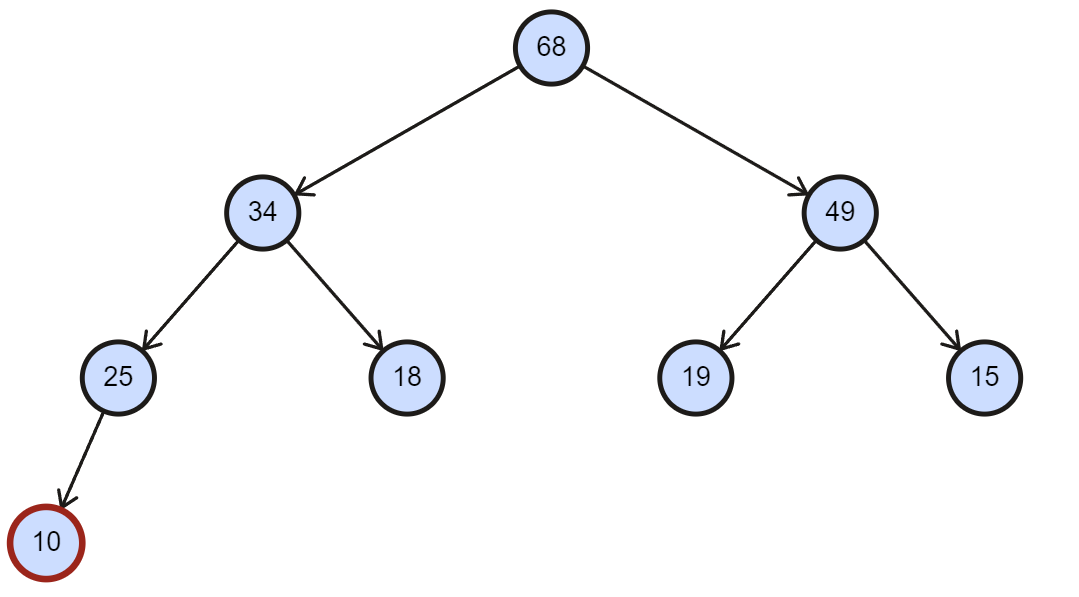
- 堆的本质实际上是个数组,因此往堆中插入数据就将数据尾插到数组中。
- 当前有一组数据为 [68, 34, 49, 25, 18, 19, 15] 的数组构成的大根堆,往最后插入一个 10。
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->capacity == hp->size) //是否要扩容{int newcapacity = hp->capacity = 0 ? 4 : 2 * hp->capacity;HPDataType* tmp = (HPDataType*)realloc(hp->data, newcapacity * sizeof(HPDataType));assert(tmp);hp->capacity = newcapacity;hp->data = tmp;}hp->data[hp->size++] = x; //插入新数据AdjustUp(hp->data, hp->size - 1); //堆向上调整
}
05. 向上调整堆
1. 为何要向上调整堆
- 插入数据之后可能导致破坏堆的结构,可能要对堆进行调整。
- 往一个堆中插入不同的值时,需要判断会不会破会堆的结构。
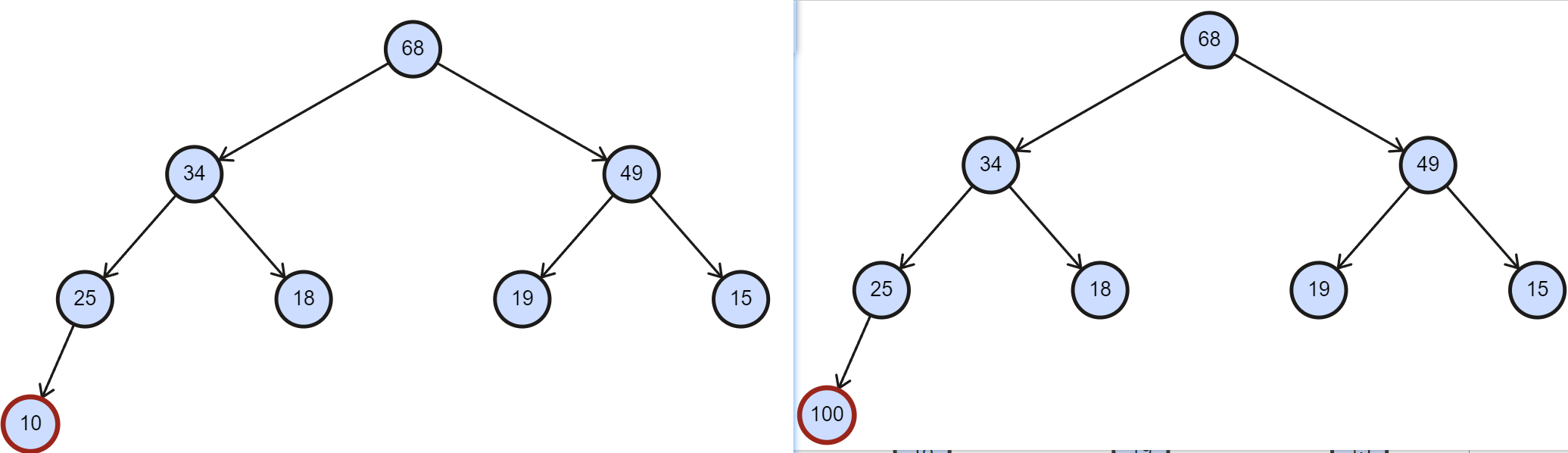
- 下图中,插入了 10 不会破坏大根堆,插入 100 却会。
2. 根据堆的性质判断是否要调堆
-
小根堆中:只需要判断新插入的数据是否 < 其双亲结点的值,如果是则和其双亲结点交换。
-
大根堆中:只需要判断新插入的数据是否 > 其双亲结点的值,如果是则和其双亲结点交换。
-
在交换了之后,新结点可能比它双亲的双亲还 小 / 大,要一直交换到符合堆的定义为止。
- 新结点 100 和它的双亲交换之后还是大于其新的双亲,要交换到符合堆定义为止。
-
如下图所示的将 100 向上调整到它最终位置,即为堆的向上调整。
3. 堆的向上调整实现思路
- 定义的函数形参 data 是一个存储堆中数据的数组,child 是新插入的结点的下标。
- 算出新结点的双亲结点,然后与其双亲结点比较,如果不符合 大 / 小根堆的定义则交换。
- 交换了之后原来双亲结点的位置就变为了新结点的位置,再算出该结点新的双亲结点去比较。
- 当将新结点向上调整到符合 大 / 小 根堆的定义时停止调整,最坏情况新结点会被调成根结点。
4. 堆的向上调整代码实现
- 该代码适用于调成 大 / 小 根堆。
void AdjustUp(HPDataType* data, int child) // 向上调整堆
{int parent = (child - 1) / 2; // 算出新结点的双亲结点while (child > 0) // 最坏情况新结点会被调成根结点{// if (data[child] < data[parent]) // 按照 小根堆 定义向上调整if (data[child] > data[parent]) // 按照 大根堆 定义向上调整{swap(&data[child], &data[parent]); // 交换双亲和孩子结点的数据child = parent; // 原双亲结点的位置给了新结点parent = (parent - 1) / 2; // 求新结点双亲的双亲的位置}else // 结点被调到符合 大/小 根堆{break; }}
}
06. 堆的创建
实现思路
- 将一组数据从第一个开始依次进堆,每放一个数据进堆就调用一次向上调整算法。
- 当前有一组数据,将它们依次插入进堆,然后调用向上调整算法。
代码实现
int main()
{int test[] = {85,9,1,7,6,7,5,45,13,54};size_t size = sizeof(test) / sizeof(test[0]);Heap hp;HeapInit(&hp);// 将 test 数组内的值依次插入进堆for (int i = 0; i < size; i++){HeapPush(&hp, test[i]);}return 0;
}
07. 获取堆顶数据
- 数组的 0 号位置就是堆顶元素,直接返回该位置的值即可。
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(hp->size > 0); // 堆中有元素可被获取return hp->data[0]; // 堆中结点的值不一定是 int 类型
}
08. 堆的删除
- 堆的删除规定删除根结点的数据,即删除堆顶结点。
实现思路
- 将堆顶元素和堆尾元素交换,然后将堆中有效数据个数 -1 即可实现删除。
代码实现
void HeapPop(Heap* hp)
{assert(hp);assert(hp->size > 0); // 堆中有元素swap(&hp->data[0], &hp->data[hp->size - 1]); // 堆顶和堆尾互换hp->size--; // 删除最后一个元素AdjustDown(hp->data, hp->size, 0); // 将堆顶元素向下调整
}
09. 向下调整堆
1. 为何要向下调整堆
- 某些情况下,堆中的某一个非叶子结点可能要比其孩子结点 大 / 小,不符合 小 / 大 根堆的定义。
- 如上图:将 9 换到根结点之后明显就破坏了大根堆的结构,要将其向下调整到合适位置。
2. 向下调整实现思路
- 比较要下沉的结点 k 的左右孩子的值,找出值较 大 / 小 的那个孩子出来。
- 如果是大根堆,就用最大孩子和 k 互换;如果是小根堆,就用最小孩子和 k 互换。
- 重复上述步骤,直到将 k 调到它应在的位置即可。
3. 向下调整代码实现
- 按照小根堆的定义向下调整
void AdjustDown(HPDataType* data, int size, int parent)
{int child = parent * 2 + 1; // 假设是结点的左孩子比较小while (child < size) // 不能超过数组的范围{// 如果右孩子 < 左孩子,则最小孩子结点换成右孩子if (child + 1 < size && data[child + 1] < data[child]){child++;}//最小孩子结点 < 其双亲结点则要交换if (data[child] < data[parent]){swap(&data[child], &data[parent]);child = child * 2 + 1;parent = parent * 2 + 1;}else{break;}}
}
- 按照大根堆的定义向下调整,将两个 if 里用于比较左右孩子大小的 < 换成 > 即可。
- 第一个 if:将 data[child + 1] < data[child] 换成
data[child + 1] > data[child] - 第二个 if:将 data[child] < data[parent] 换成
data[child] > data[parent]
- 第一个 if:将 data[child + 1] < data[child] 换成
void AdjustDown(HPDataType* data, int size, int parent)
{int child = parent * 2 + 1; // 假设是结点的左孩子比较大while (child < size) // 不能超过数组的范围{// 如果右孩子 > 左孩子,则最大孩子结点换成右孩子if (child + 1 < size && data[child + 1] > data[child]){child++;}//最大孩子结点 > 其双亲结点则要交换if (data[child] > data[parent]){swap(&data[child], &data[parent]);child = child * 2 + 1;parent = parent * 2 + 1;}else{break;}}
}
10. 判断堆空
- 判断堆中有效数据的个数是否为 0 即可。
int HeapEmpty(Heap* hp)
{assert(hp);return 0 == hp->size;
}
🌈 Ⅳ 堆的基本应用
01. 堆排序的实现
排序思路
- 事先声明:排升序用大根堆,排降序用小根堆 (默认为升序)
- 将待排序的 n 个数据使用向下调整造成一个大根堆,此时堆顶就是整个数组的最大值。
- 将堆顶和堆尾互换,此时堆尾的数就变成了最大值,剩余的待排序数组元素个数为 n - 1 个。
- 将剩余的 n - 1 个数调整回大根堆,将新的大根堆的新的堆顶和新的堆尾互换。
- 重复执行上述步骤,即可得到有序数组。
举个例子
- 当前有数据为 [ 8, 9, 4, 74, 12, 15, 6 ] 现对其进行升序排序,要先构成大根堆。
代码实现
- data 指向原数组空间,n 表示要排序的数据个数。
// 排成升序
void HeapSort(int* data, int n)
{int i = 0;int end = n - 1;// 从最后一个非叶子结点开始依次往前向下调整构建大根堆// n - 1 是最后一个结点的下标,(n - 1 - 1) / 2 是最后一个结点的夫结点下标// 也就是最后一个非叶子结点for (i = (n - 1 - 1) / 2; i >= 0; i--){// 要使用建大堆的向下调整算法AdjustDown(data, n, i);}// 0 和 end 夹着的是待排序数据,end 是待排序数据的个数// 每次都选出一个最大的数放到 end 处,然后待排序数据个数 end - 1while (end > 0){swap(&data[0], &data[end]); // 互换堆顶和堆尾的数据AdjustDown(data, end, 0); // 从根位置 (0) 开始的向下调整end--; // 缩小待排序数据区间,且个数 - 1}
}
02. TOP K 问题
问题概述
- 在 n 个数中找出最大 / 最小的前 k 个数 (前提:n 远大于 k)
实现思路
- 用这 n 个数的前 k 个数来构建一个堆,这个堆就只有 k 个数。
- 求前 k 个最大的元素,就建小根堆。
- 求前 k 个最小的元素,就建大根堆。
- 用剩余的 n - k 个元素依次与堆顶元素比较。
- 求前 k 个最大的元素,就用比小根堆顶 大 的数和其互换,然后向下调整堆。
- 求前 k 个最小的元素,就用比大根堆顶 小 的数和其互换,然后向下调整堆。
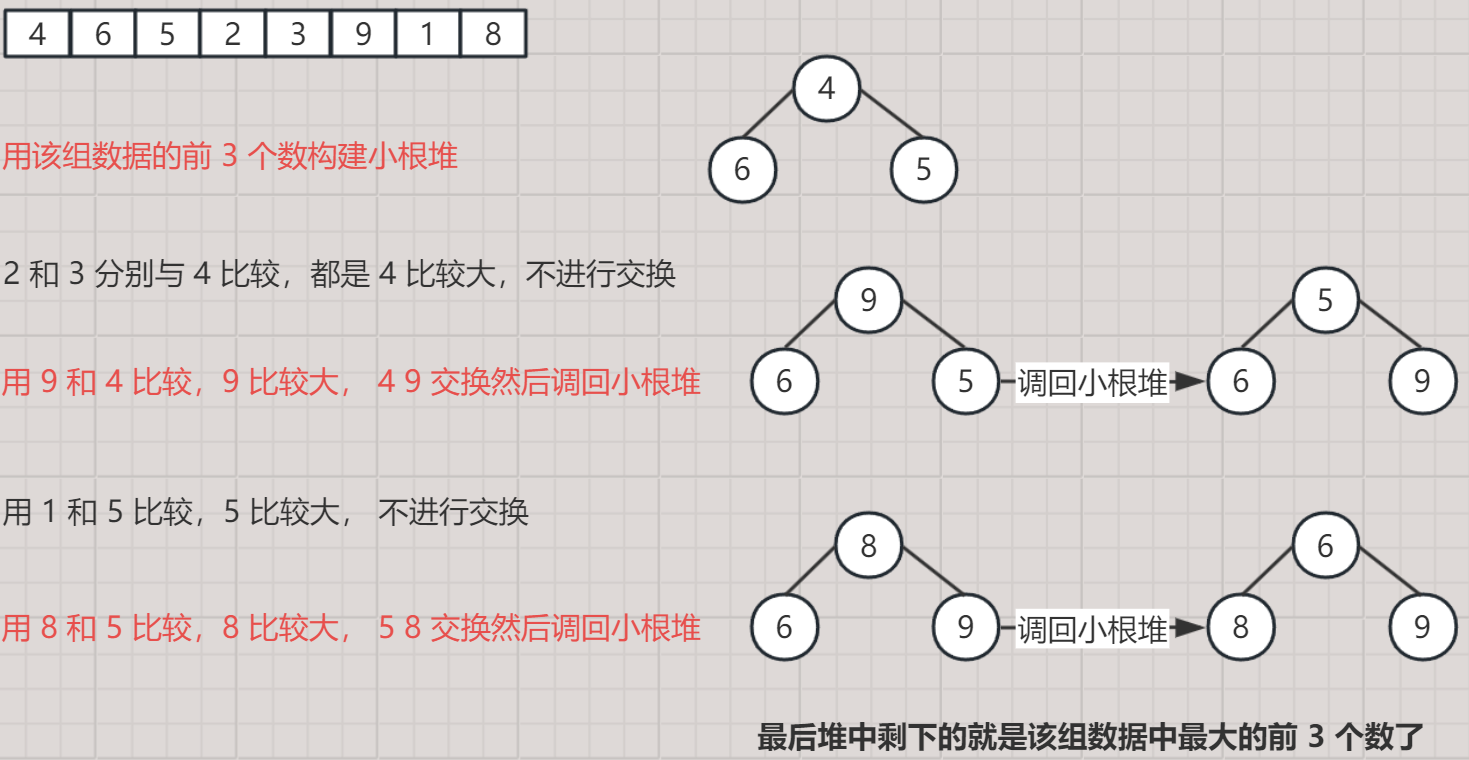
举个栗子
- 当前有如下一组数据,现求其最大的前 3 个数
- [ 4, 6, 5, 2, 3, 7, 9, 1, 8 ]
- 建成小堆能将后面比堆顶小的数全部挡在外面,最后堆中剩下的 3 个值就是最大的那三个。
代码实现
void TopK(int* data, int n, int k)
{int i = 0;int j = 0;HPDataType* MinHeap = (HPDataType*)malloc(sizeof(HPDataType) * k);assert(MinHeap);for (i = 0; i < k; i++) // 将前 k 个数先插入进堆中{MinHeap[i] = data[i];}for (i = (k - 2) / 2; i >= 0; i--) // 将这 k 个数的堆向下调整成小根堆{AdjustDown(MinHeap, k, i);}for(j = k; j < n; j++) // 将 k 之后的数据依次和堆顶比较{if (MinHeap[0] < data[j]) // 后续数据大于堆顶则和堆顶互换后调整{MinHeap[0] = data[j];AdjustDown(MinHeap, k, 0);}}
}
相关文章:
【数据结构初阶 6】二叉树:堆的基本操作 + 堆排序的实现
文章目录 🌈 Ⅰ 二叉树的顺序结构🌈 Ⅱ 堆的概念与性质🌈 Ⅲ 堆的基本操作01. 堆的定义02. 初始化堆03. 堆的销毁04. 堆的插入05. 向上调整堆06. 堆的创建07. 获取堆顶数据08. 堆的删除09. 向下调整堆10. 判断堆空 🌈 Ⅳ 堆的基本…...
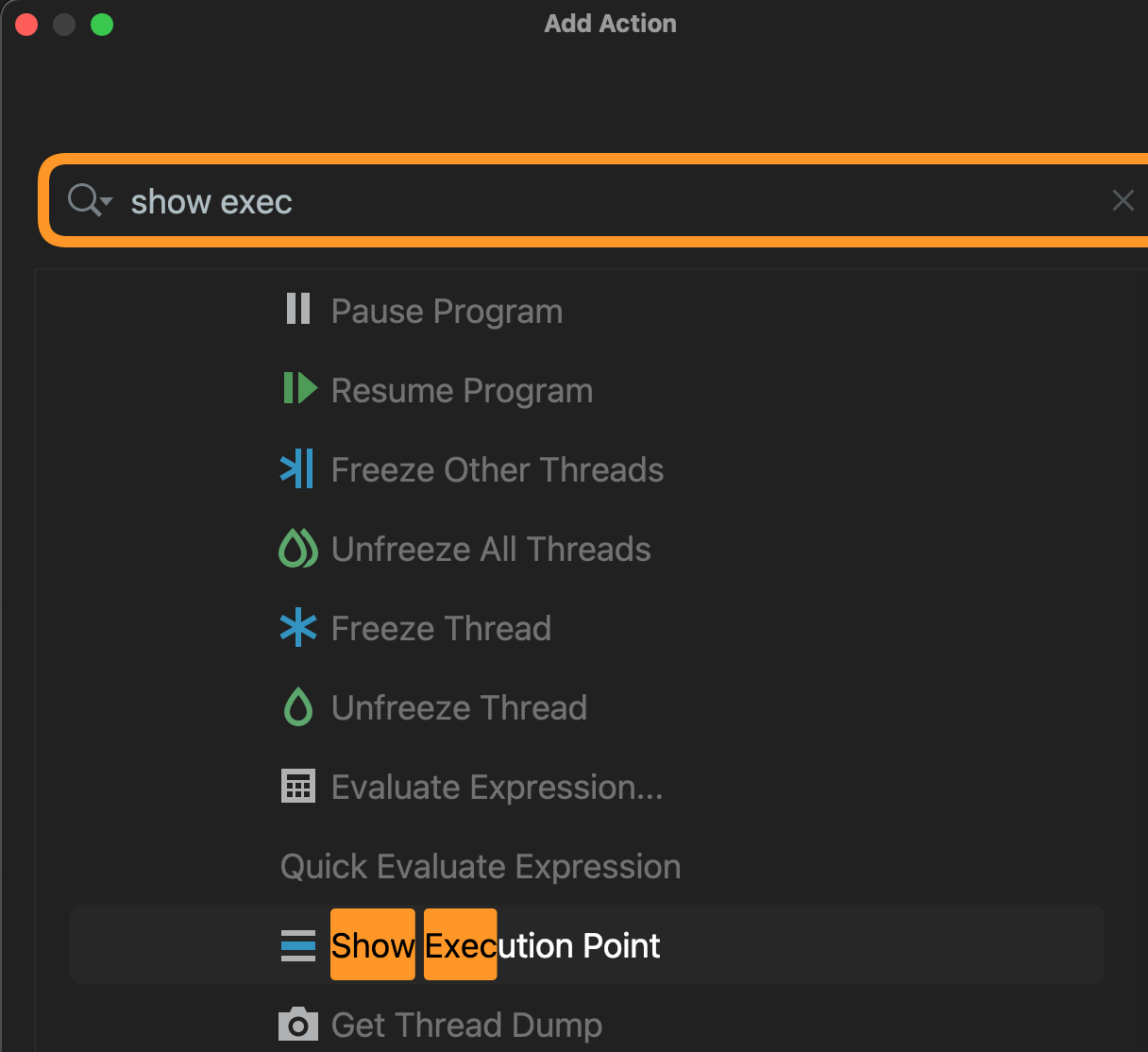
IDEA Debug框的 show execution point按钮没了
在这里右键: Add Action: 搜索添加: 本文由博客一文多发平台 OpenWrite 发布!...
))
突破编程_C++_面试(类(1))
面试题 1 :解释一下 C 中的类是什么,它有哪些基本特性? C 中的类(class)是面向对象程序设计的基本构成单位,它是一种自定义的数据类型,用于封装数据以及操作这些数据的方法。类是创建对象的模板…...

vue项目使用vue2-org-tree
实现方式 安装依赖 npm i vue2-org-tree使用的vue页面引入 <template><div class"container"><div class"oTree" ><vue2-org-tree name"test":data"data":horizontal"horizontal":collapsable"…...

Vue30 自定义指令 函数式 对象式
实例 <!DOCTYPE html> <html><head><meta charset"UTF-8" /><title>自定义指令</title><script type"text/javascript" src"../js/vue.js"></script></head><body><!-- 需求1&…...
JAVA高并发——单例模式和不变模式
文章目录 1、探讨单例模式2、不变模式 由于并行程序设计比串行程序设计复杂得多,因此我强烈建议大家了解一些常见的设计方法。就好像练习武术,一招一式都是要经过学习的。如果自己胡乱打,效果不见得好。前人会总结一些武术套路,对…...
RabbitMQ(一):消息队列MQ
目录 1 消息队列MQ1.1 MQ简介1、什么是MQ2、MQ的优势流量削峰应用解耦异常处理数据分发分布式事务 3、消息中间件的弊端4、常用的MQ 1.2 MQ中几个基本概念1.3 MQ的通信模式1.4 消息的发布策略1.5 常用消息中间件协议1、AMQP协议2、MQTT协议3、OpenMessage协议4、kafaka协议 1 消…...
HarmonyOS—使用预览器查看应用/服务效果
DevEco Studio为开发者提供了UI界面预览功能,可以查看应用/服务的UI界面效果,方便开发者随时调整界面UI布局。预览器支持布局代码的实时预览,只需要将开发的源代码进行保存,就可以通过预览器实时查看应用/服务运行效果,…...

大项目中,某个cpp文件读取所在包路径的方法
在一个比较大的C项目中,我们有很多包,每个包都有一个自己的src、include、CMakeLists.txt和其它文件,比如以下文件结构: project- pkg1- datas- data.json- src- xxx1.cpp- include- xxx1.h - CMakeLists.txt- pkg2- src- xxx2.…...
:用于异构SoC的片上网络模型——Garnet2.0)
gem5学习(25):用于异构SoC的片上网络模型——Garnet2.0
目录 一、Invocation 二、Configuration 三、Topology 四、Routing 五、Flow Control 六、Router Microarchitecture 七、Buffer Management 八、Lifecycle of a Network Traversal 九、Running Garnet2.0 with Synthetic Traffic 官网教程:gem5: Garnet 2…...
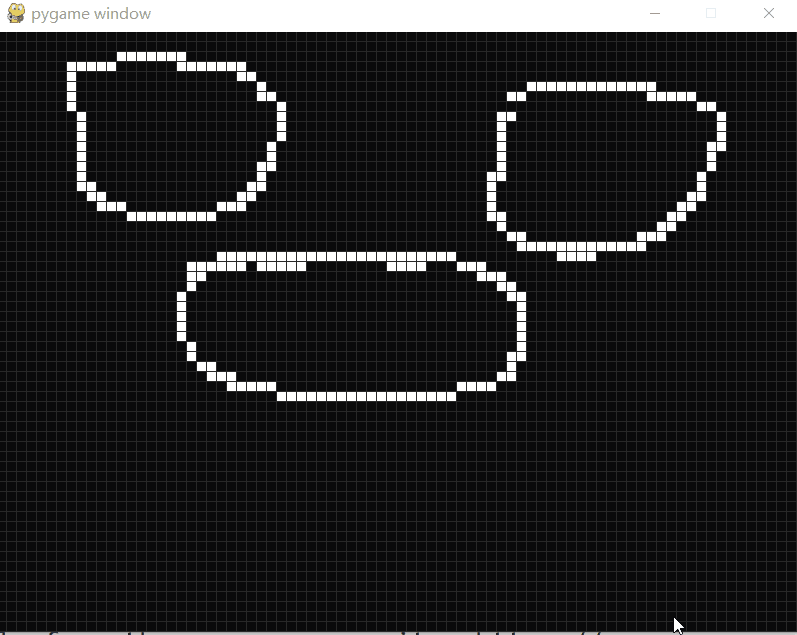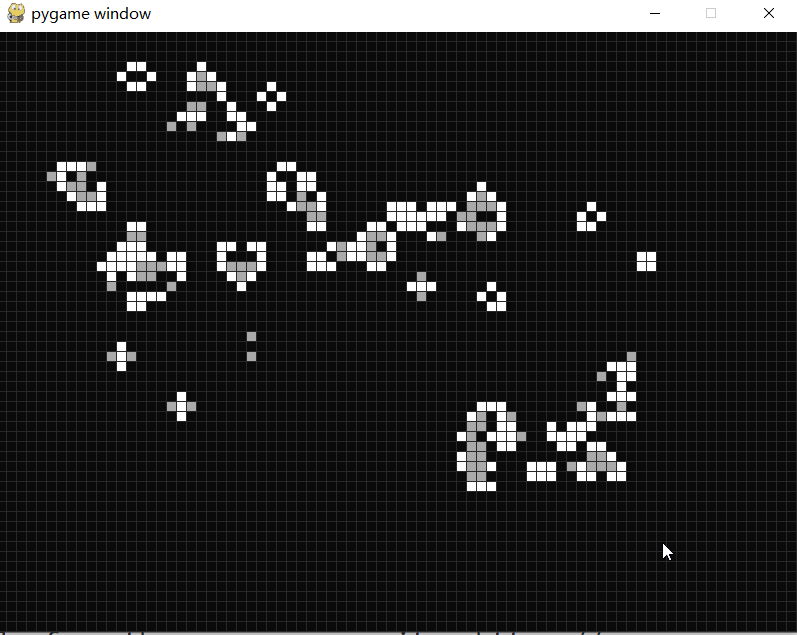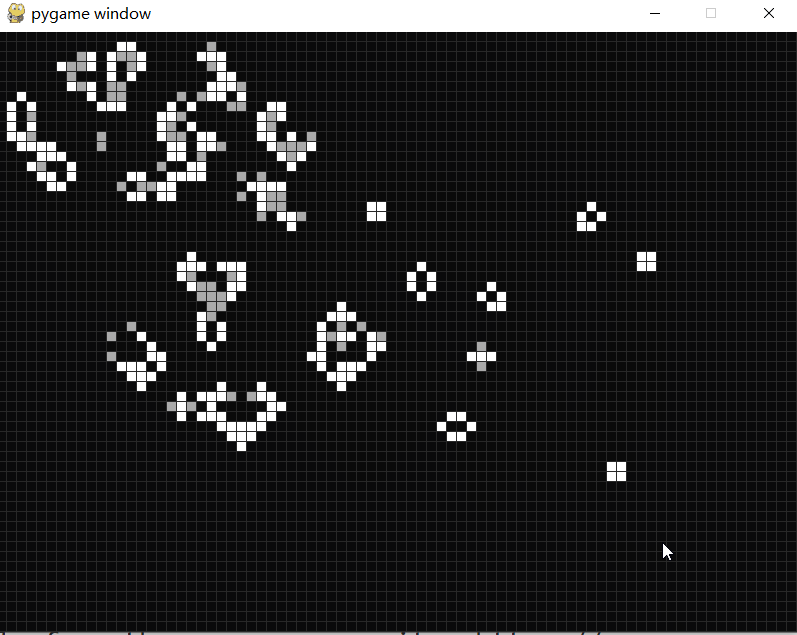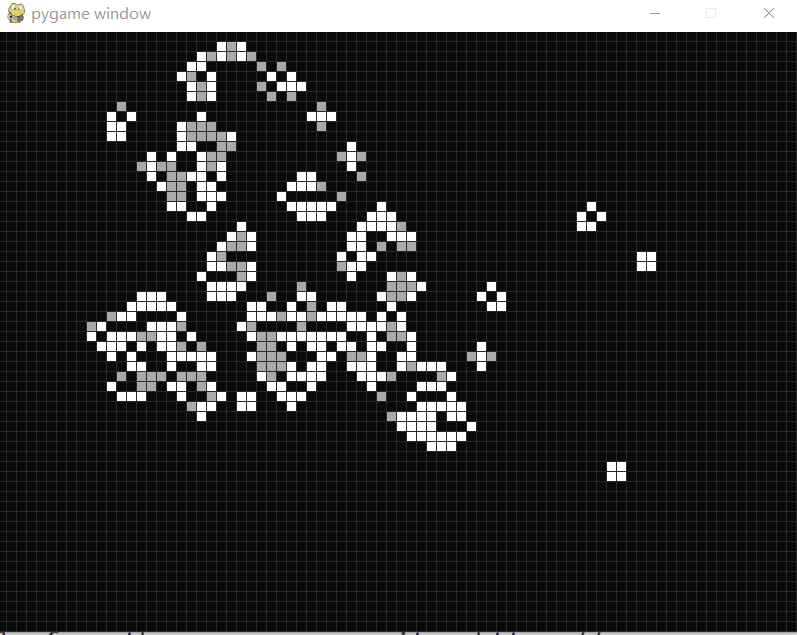
康威生命游戏
康威生命游戏 康威生命游戏(Conway’s Game of Life)是康威发明的细胞自动机。 生命游戏有几个简单的规则: 细胞有两种状态,存活或死亡,每个细胞以自身为中心与周围的八格细胞互动。 对于存活的细胞: 当周围的细胞过少(<2)或…...

vscode与vue环境配置
一、下载并安装VScode 安装VScode 官网下载 二、配置node.js环境 安装node.js 官网下载 会自动配置环境变量和安装npm包(npm的作用就是对Node.js依赖的包进行管理),此时可以执行 node -v 和 npm -v 分别查看node和npm的版本号: 配置系统变量 因为在执…...
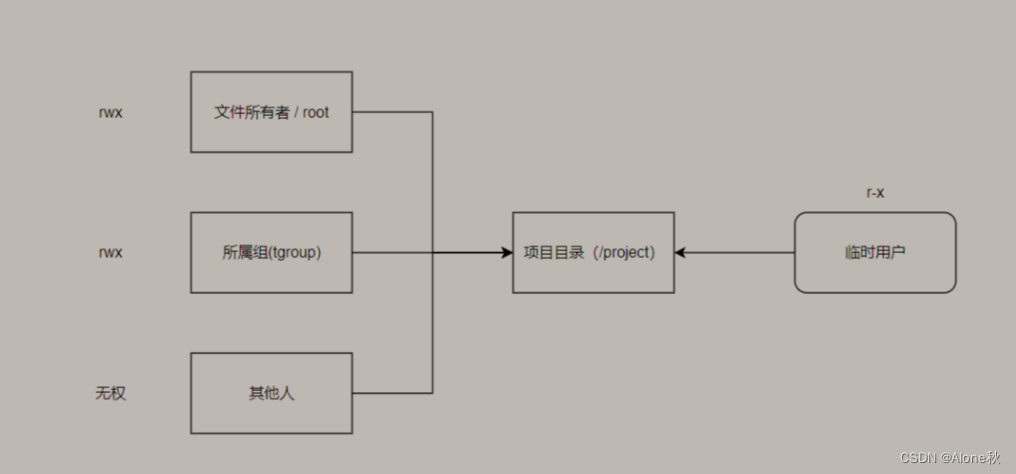
Linux的ACL权限以及特殊位和隐藏属性
前言: ACL是什么? ACL(Access Control List)是一种权限控制机制,用于在Linux系统中对文件和目录进行细粒度的访问控制。传统的Linux权限控制机制基于所有者、所属组和其他用户的三个权限类别(读、写、执行…...
使用openai-whisper实现语音转文字
使用openai-whisper实现语音转文字 1 安装依赖 1.1 Windows下安装ffmpeg FFmpeg是一套可以用来记录、转换数字音频、视频,并能将其转化为流的开源计算机程序。采用LGPL或GPL许可证。它提供了录制、转换以及流化音视频的完整解决方案。 # ffmpeg官网 https://ffm…...

C++模板为什么不能声明和定义分离
首先我们要直到C程序运行需要进行的四个阶段。 预处理->编译->汇编->链接 编译:对语法语义分析,分析无误生成汇编,头文件不参加编译,多个源文件是分开单独编译的。 链接:将多个obj文件链接合成一个&#x…...
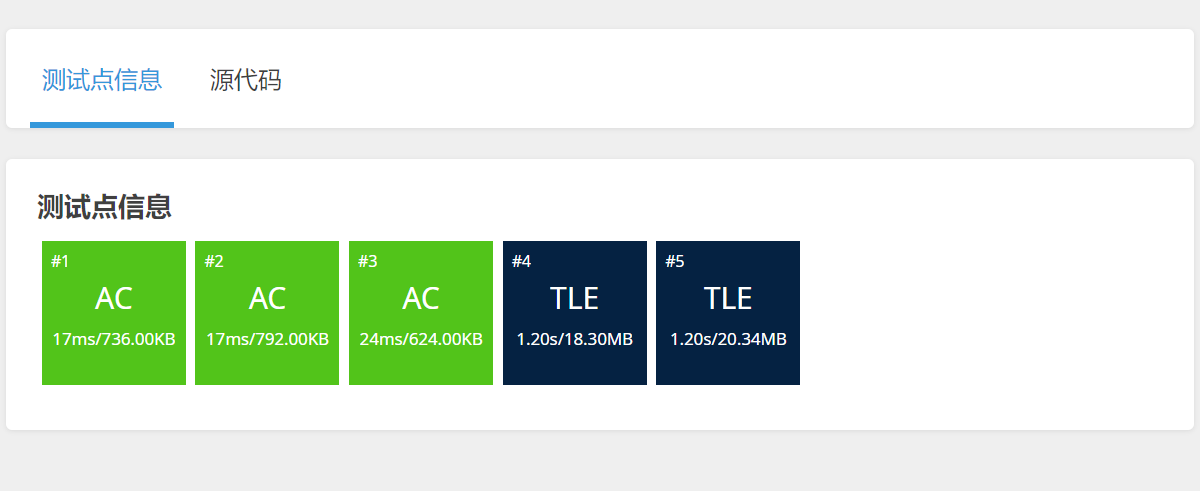
啊丢的刷题记录手册
1.洛谷题P1923 求第k小的数 题目描述 输入 n(1≤n<5000000 且 n 为奇数)个数字ai(1≤ai<109),输出这些数字的第 k 小的数。最小的数是第 0 小。 请尽量不要使用 nth_element 来写本题,因为本题…...

用nginx正向代理https网站
目录 1. 缘起2. 部署nginx3. 测试3.1 http测试3.2 https测试4 给centos设置代理访问外网 1. 缘起 最近碰到了一个麻烦事情,就是公司的centos测试服务器放在内网环境,而且不能直接上外网,导致无法通过yum安装软件,非常捉急。 幸…...

面向对象设计模式
一、单例 一个类只能创建唯一一个对象 利用限制构造、static完成 二、工厂模式 优势:规范接口(纯虚函数);实现多态(虚函数表);继承 1、简单工厂 一个工厂创建所有产品。 返回基类指针可…...

人工智能_CPU微调ChatGLM大模型_使用P-Tuning v2进行大模型微调_007_微调_002---人工智能工作笔记0102
这里我们先试着训练一下,我们用官方提供的训练数据进行训练. 也没有说使用CPU可以进行微调,但是我们先执行一下试试: https://www.heywhale.com/mw/project/6436d82948f7da1fee2be59e 可以看到说INT4量化级别最低需要7GB显存可以启动微调,但是 并没有说CPU可以进行微调.我们…...
Android自编译Pixel3内核加入KernelSU
背景 让Pixel3 AOSP Android10 4.9内核用上Kernel SU 环境: Ubuntu 18.04 vm aosp10r2 移植参考官方,和github项目 Commits OnlyTomInSecond/android_kernel_xiaomi_sdm845 (github.com) 这个项目是 LineageOS/android_kernel_xiaomi_sdm845 编译的前提 已经有完整…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...