算法打卡day1|数组篇|Leetcode 704.二分查找、27.移除元素
数组理论基础
数组是存放在连续内存空间上的相同类型数据的集合,可以方便的通过下标索引的方式获取到下标下对应的数据。
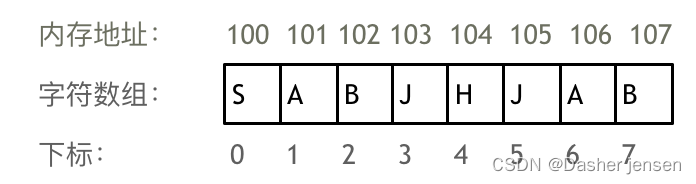
1.数组下标都是从0开始的。
2.数组内存空间的地址是连续的。
正是因为数组的在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址所以数组的元素是不能删的,只能覆盖。
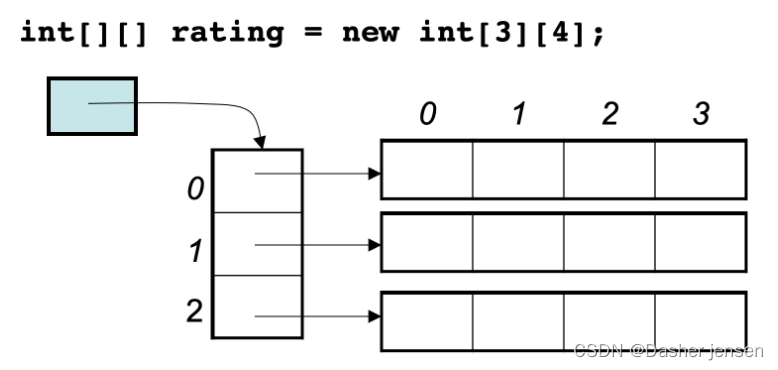
在C++中二维数组在内存的空间地址是连续,但在java中并不是连续的。
java中的数组排列方式如下,所以Java的二维数组在内存中不是 3*4 的连续地址空间,而是四条连续的地址空间组成!
算法题
Leetcode 704.二分查找
题目链接:二分查找
大佬视频讲解:手把手带你撕出正确的二分法
个人思路
题目要求是用二分法;那具体步骤为:找到数组中间的值,将这个值循环与目标值对比,1.若找到目标值放回下标2.没找到目标值的话,则按照与目标值对比的大小,重新选择范围,再选择这个范围中的中间值继续对比;但这其中比较难解决的是范围的确定。
解法
这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因此以后遇到此种类型都可以考虑使用二分法;
二分法中,对区间的定义很重要。区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
二分法第一种写法:左闭右闭
即[left, right];左闭右闭要注意以下两点
- 循环while中的判断条件 “(left <= right) ”要使用 <= ,因为left == right是有意义的。
- 目标值小于中间值,右区间需要改变时;right 要赋值为 mid - 1,因为当前这个nums[middle]一定不是target。
class Solution {public int search(int[] nums, int target) {int left=0;int right=nums.length-1;//定义target在左闭右闭的区间里,[left, right]if(target <nums[0]||target>nums[right-1]){//避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算return -1;}while(left<=right){int mid=left+((right-left)>>1);//防止溢出;>> 是右移位运算符,相当于除以 2 并向下取整if(nums[mid]==target){return mid;}else if(nums[mid]<target){//target 在右区间,即[mid + 1, right]left=mid+1;}else if(nums[mid]>target){//target 在左区间,即[left, mid- 1]right=mid-1;}}return -1;}
}时间复杂度:O(log n);(折半循环)
空间复杂度:O(1);(没有使用多余空间)
二分法第二种写法:左闭右开
即[left, right);左闭右开要注意以下两点
- 循环while中的判断条件“(left < right)”,这里使用 < ,因为left == right在区间[left, right)是没有意义的
- 目标值小于中间值,右区间需要改变时, right 更新为 mid,因为下一个查询区间不会去比较nums[middle]
class Solution {public int search(int[] nums, int target) {int left=0;int right=nums.length;//定义target在左闭右开的区间里,[left, right]if(target <nums[0]||target>nums[right-1]){//避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算return -1;}while(left<right){int mid=left+((right-left)>>1);//防止溢出;>> 是右移位运算符,相当于除以 2 并向下取整if(nums[mid]==target){return mid;}else if(nums[mid]<target){//target 在右区间,即[mid + 1, right)left=mid+1;}else if(nums[mid]>target){//target 在左区间,即[left, mid)right=mid;}}return -1;}
}时间复杂度:O(log n);(折半循环)
空间复杂度:O(1);(没有使用多余空间)
Leetcode27.移除元素
题目链接:27.移除元素
大佬视频讲解:数组中移除元素并不容易
个人思路
因为数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖,所以若要暴力解决的话,得两次循环,一次循环找与目标值对应的,二次循环将删除元素其后面的元素向前赋值;
这种解法慢,也可以换成双指针来解决,指针分为快慢指针,快指针找需要删除的元素,慢指针找新数组的下标;
解法
暴力解法
双重循环
class Solution {public int removeElement(int[] nums, int val) {int len= nums.length;for (int i = 0; i < len; i++) {if (nums[i] == val) { // 发现需要移除的元素,就将数组集体向前移动一位for (int j = i + 1; j < len; j++) {nums[j - 1] = nums[j];}i--; // 因为下标i以后的数值都向前移动了一位,所以i也向前移动一位len--; // 此时数组的大小-1}}return len;}
}时间复杂度:O(n^2);(两个for循环 n*n)
空间复杂度:O(1);(没有使用多余空间)
快慢双指针
搞清楚双指针的定义非常关键,快指针的作用是寻找新数组的元素 ,新数组就是不含有目标元素的数组;慢指针的作用是指向更新 新数组下标的位置
class Solution {public int removeElement(int[] nums, int val) {int slow=0;//慢指针for(int fast=0;fast<nums.length;fast++){if(nums[fast]!=val){//如果没有找到目标元素则一起向前遍历nums[slow]=nums[fast];slow++;}}return slow;}
}时间复杂度:O( n);(一个for循环)
空间复杂度:O(1);(没有使用多余空间)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网
相关文章:

算法打卡day1|数组篇|Leetcode 704.二分查找、27.移除元素
数组理论基础 数组是存放在连续内存空间上的相同类型数据的集合,可以方便的通过下标索引的方式获取到下标下对应的数据。 1.数组下标都是从0开始的。 2.数组内存空间的地址是连续的。 正是因为数组的在内存空间的地址是连续的,所以我们在删除或者增添…...

什么是高阶组件
高阶组件(HOC)是 React 中用于复用组件逻辑的一种高级技巧。简单来说,高阶组件就是一个函数,该函数接受一个组件作为参数,并返回一个新的组件。这个新的组件会使用你传给它的组件作为子组件。 高阶组件并不是真的组件…...

python实现裂区试验方差分析
方差分析(Analysis of Variance,ANOVA)是一种统计方法,用于比较三个或三个以上组别的平均值是否存在显著差异。它通过比较组内变异和组间变异的大小来判断组别间的平均值是否有显著差异。 方差分析通常用于以下情况: …...

Vue v-for、v-if、v-show常见问题
vue使用v-for遍历对象时,是按照什么顺序遍历的?如何保证顺序? 会先判断对象是否存在iterator接口,如果有循环执行next()方法。 没有iterator的情况下,会调用Object.Keys()方法,在不同的浏览器中ÿ…...

GPT技术在学术研究中的革命性应用:开启论文创作新篇章
在学术界,撰写高质量的论文一直是一个挑战性的任务,它不仅需要深厚的专业知识,还要求良好的文献综述能力、数据分析技巧以及清晰的表达能力。近年来,随着人工智能技术的飞速发展,尤其是生成式预训练变换器(…...

【K8s】-- 描述容器中 pod 的状态
命令:kubectl describe pod -n 你的namespace名称 pod 名称 举例:kubectl describe pod -n my-flink --context prod-5 test-record-all-new-mc-taskmanager-1-1 Name: test-record-all-new-mc-taskmanager-1-1 Namespace: ky-flink Pri…...

使用yolo-seg模型实现自定义自动动态抠图
yolov8导航 如果大家想要了解关于yolov8的其他任务和相关内容可以点击这个链接,我这边整理了许多其他任务的说明博文,后续也会持续更新,包括yolov8模型优化、sam等等的相关内容。 YOLOv8(附带各种任务详细说明链接) …...
FairyGUI × Cocos Creator 3.x 场景切换
前言 前文提要: FariyGUI Cocos Creator 入门 FairyGUI Cocos Creator 3.x 使用方式 个人demo:https://gitcode.net/qq_36286039/fgui_cocos_demo_dust 个人demo可能会更新其他代码,还请读者阅读本文内容,自行理解并实现。 官…...

【Java程序设计】【C00288】基于Springboot的篮球竞赛预约平台(有论文)
基于Springboot的篮球竞赛预约平台(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的篮球竞赛预约平台 本系统分为前台功能模块、管理员功能模块以及用户功能模块。 前台功能模块:用户进入到平台首页&a…...

textbox文本框跨线程写入,扩展textobx控件
在Windows Forms中,由于UI控件不是线程安全的,直接跨线程访问和修改UI控件通常会导致不可预测的行为或异常。TextBox 控件同样不能直接从非创建它的线程进行写入。为了安全地在不同线程间更新 TextBox 控件的内容,你可以使用控件的 Invoke 方…...
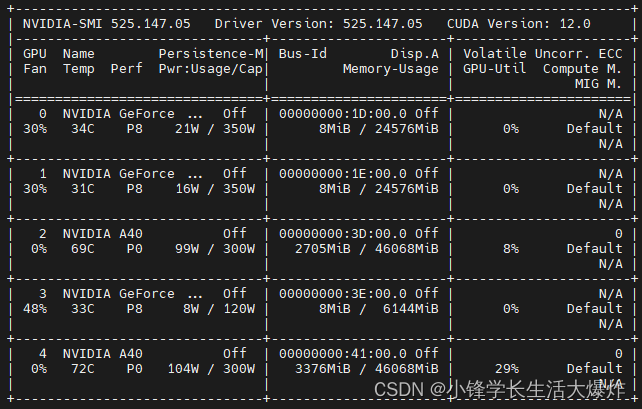
【踩坑】PyTorch中指定GPU不生效和GPU编号不一致问题
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 指定GPU不生效问题 解释:就是使用os.environ["CUDA_VISIBLE_DEVICES"] "1"后,后面使用起来仍然是cuda0. 解决:在最开头就使用 import os os.environ[&…...
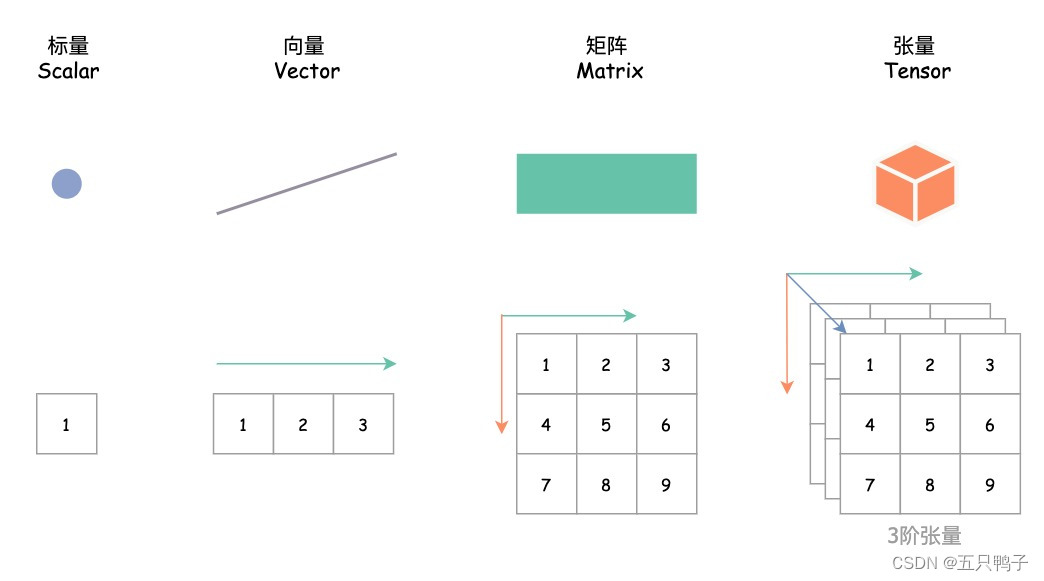
线性代数:向量、张量、矩阵和标量
线性代数:向量、张量、矩阵和标量 背景 在线性代数中,向量、张量、矩阵和标量都属于基础概念,特别是最近AI的爆火,向量和张量的概念也越来越普及,本文将介绍下这些基本概念。 1. 标量(Scalar࿰…...

WordPres Bricks Builder 前台RCE漏洞
免责声明:文章来源互联网收集整理,请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该…...
渗透测试—信息收集
渗透测试—信息收集 1. 收集域名信息1.1. 域名注册信息1.2. SEO信息收集1.3. 子域名收集1.3.1. 在线子域名收集1.3.2. 子域名收集工具 1.4. 域名备案信息1.5. ICP备案号查询1.6. SSL证书查询 2. 收集真实IP2.1. 超级ping2.2. Ping2.3. CDN绕过 3. 收集旁站或C段IP3.1. 旁站或C段…...
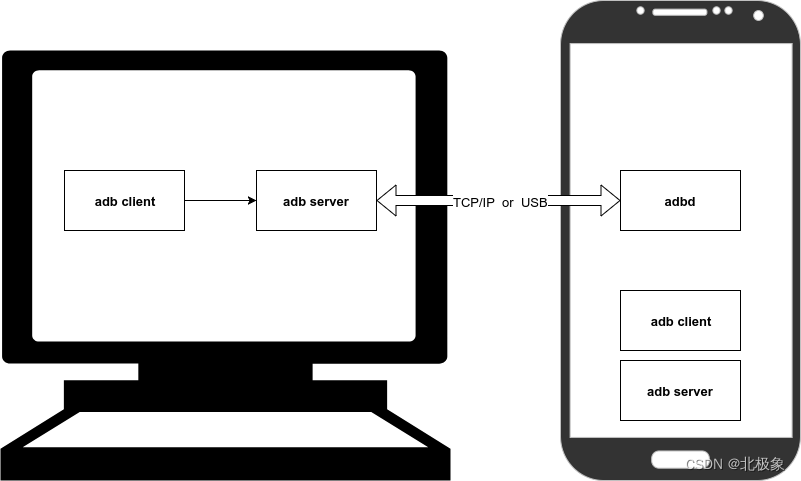
安卓adb调试备忘录
由于 MAC 的 USB 口全被占用着,采用无线连接刚方便,记录一下,以防忘记~ ADB原理 adb devices -l ## 列出连接的设备adb tcpip [端口号] adb tcpip 6666 # 将当前已连接USB上的Mobile端切换为TCP/IP模式,以6666端口进行监听. adb…...
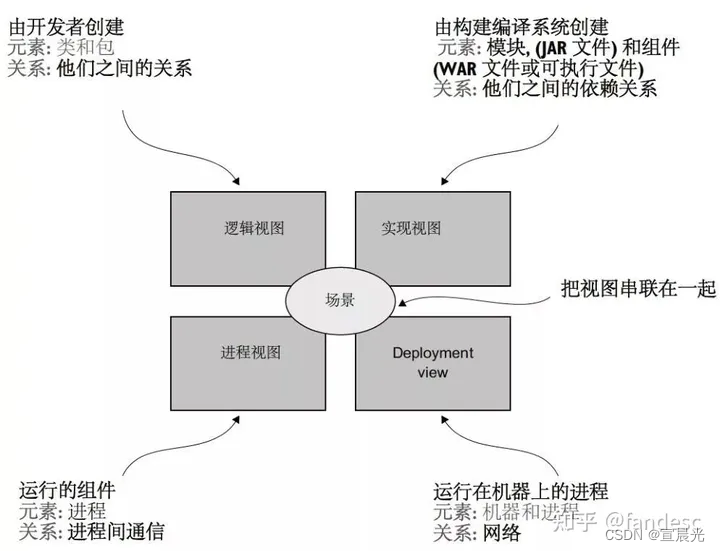
【软件架构】01-架构的概述
1、定义 软件架构就是软件的顶层结构 RUP(统一过程开发)4 1 视图 1)逻辑视图: 描述系统的功能、组件和它们之间的关系。它主要关注系统的静态结构,包括类、接口、包、模块等,并用于表示系统的组织结构…...

Vue 图片轮播第三方库 介绍
Vue图片轮播是一种在网页上以自动或手动方式展示图片的组件,常用于产品展示、网站banner等场景。有许多第三方库可以帮助Vue开发者轻松实现图片轮播功能。以下是一些流行的Vue图片轮播第三方库的介绍: 1. Vue-awesome-swiper - **简介**:V…...

设置主从复制时发生报错Could not find first log file name in binary log index file‘;解决方案
如图所示,slave_io_runnind:no,slave_sql_running:yes 此时,主从配置错误,我们可以查看Last_IO_Error:来查看报错信息 此时,我们需要停止从服务器的主从服务, mysql> stop slave; Query OK, 0 rows affected, 1 w…...

React Context的使用方法
背景:在某些场景下,你想在整个组件树中传递数据,但却不想手动地在每一层传递属性,你可以直接在React中使用强大的contextAPI 解决上述问题 在一个典型的React 中,数据通过Props属性自下而上(由父及子&…...

ElasticSearch索引数据备份与恢复
索引数据备份 在磁盘创建备份目录并授权 # 创建备份目录 /home/esbackup # 授权 chmod 777 /home/esbackup修改配置文件elasticsearch.yml echo path.repo: ["/home/esbackup"] >> /etc/elasticsearch/elasticsearch.yml重启elasticsearch(我是docker创建的…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
