线性代数:向量、张量、矩阵和标量
线性代数:向量、张量、矩阵和标量
背景
在线性代数中,向量、张量、矩阵和标量都属于基础概念,特别是最近AI的爆火,向量和张量的概念也越来越普及,本文将介绍下这些基本概念。
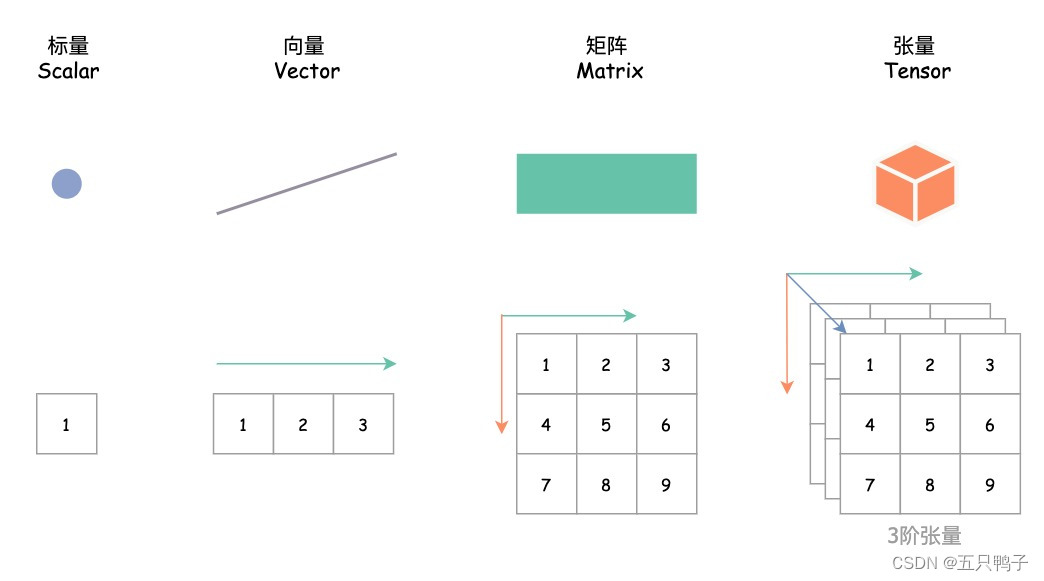
1. 标量(Scalar)
1.1 定义和表示
标量是数学中的一个基本概念,它表示一个单独的实数,没有方向或位置。在数学表示中,我们通常用小写字母表示标量,例如 a 或 x。
1.2 例子
- 温度(32℃)
- 质量(62kg)
- 速度(102km/h)
标量是我们日常生活中常见的量,它们具有大小但没有方向。
在python代码中表示
x = 1# 或者可以表示为0阶张量x = np.array(1)print(x.ndim)
2. 向量(Vector)
2.1 定义和表示
向量是有序的一维数组,其中包含多个标量元素。每个元素都有一个索引,表示其在向量中的位置。在数学表示中,我们通常用小写粗体字母表示向量,如 v。
2.2 例子
- 位移(向东200米)
- 力(向左10牛米)
向量不仅有大小,还有方向,因此它可以表示在空间中的运动或力的作用方向。
2.3 代码和图示
一个二维向量可以表示为
v = [ 1 2 3 ] v = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} v=[123]
在python代码中表示
v = np.array([1, 2, 3])print(v.ndim) # = 1
3. 矩阵(Matrix)
3.1 定义和表示
矩阵是一个二维数组,其中包含多个标量元素,这些元素按行和列排列。在数学表示中,我们通常用大写字母表示矩阵,如 A。
3.2 例子
- 图像的像素值
- 线性变换
公式和图示
一个 m x n 的矩阵 A 可以表示为:
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} A= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn
在python代码中例子
m = np.array([[1, 2], [3, 4]])print(m.ndim) # = 2
4. 张量(Tensor)
4.1 定义和表示
在线性代数里面可以简单的将张量理解为一个多维数组,可以包含标量、向量和矩阵。在数学表示中,我们通常用大写粗体字母表示张量,如 T
4.2 例子
- 神经网络中的输入
- 多模态数据的表示,如图片语音视频等
公式和图示
在深度学习中,一个三维张量 T 可以表示为:
T = [ A B C D E F G H I ] \mathbf{T} = \begin{bmatrix} \mathbf{A} & \mathbf{B} & \mathbf{C} \\ \mathbf{D} & \mathbf{E} & \mathbf{F} \\ \mathbf{G} & \mathbf{H} & \mathbf{I} \end{bmatrix} T= ADGBEHCFI
这里A、B、C、D等可以是标量、向量或矩阵。
之间的关系
- 标量是零阶张量,向量是一阶张量,矩阵是二阶张量。
- 张量的阶数表示它包含的维度数量,不止是3阶张量,张量可以是无数阶。
- 从这种角度来看,万物皆张量
相关文章:

线性代数:向量、张量、矩阵和标量
线性代数:向量、张量、矩阵和标量 背景 在线性代数中,向量、张量、矩阵和标量都属于基础概念,特别是最近AI的爆火,向量和张量的概念也越来越普及,本文将介绍下这些基本概念。 1. 标量(Scalar࿰…...

WordPres Bricks Builder 前台RCE漏洞
免责声明:文章来源互联网收集整理,请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该…...
渗透测试—信息收集
渗透测试—信息收集 1. 收集域名信息1.1. 域名注册信息1.2. SEO信息收集1.3. 子域名收集1.3.1. 在线子域名收集1.3.2. 子域名收集工具 1.4. 域名备案信息1.5. ICP备案号查询1.6. SSL证书查询 2. 收集真实IP2.1. 超级ping2.2. Ping2.3. CDN绕过 3. 收集旁站或C段IP3.1. 旁站或C段…...
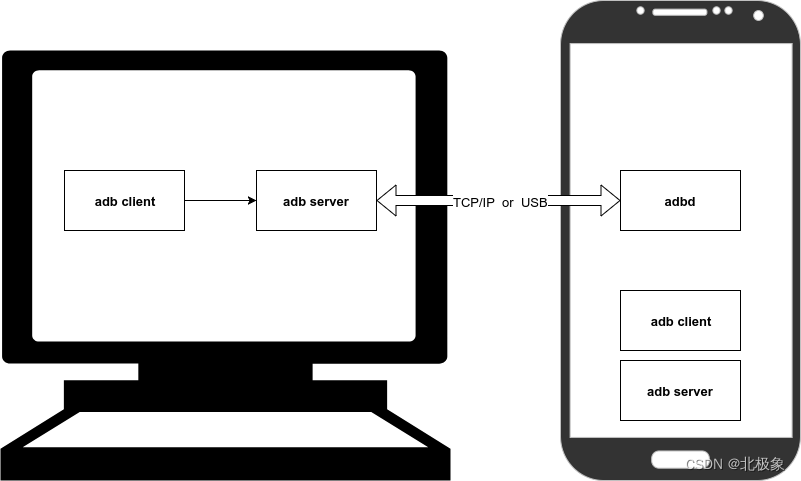
安卓adb调试备忘录
由于 MAC 的 USB 口全被占用着,采用无线连接刚方便,记录一下,以防忘记~ ADB原理 adb devices -l ## 列出连接的设备adb tcpip [端口号] adb tcpip 6666 # 将当前已连接USB上的Mobile端切换为TCP/IP模式,以6666端口进行监听. adb…...
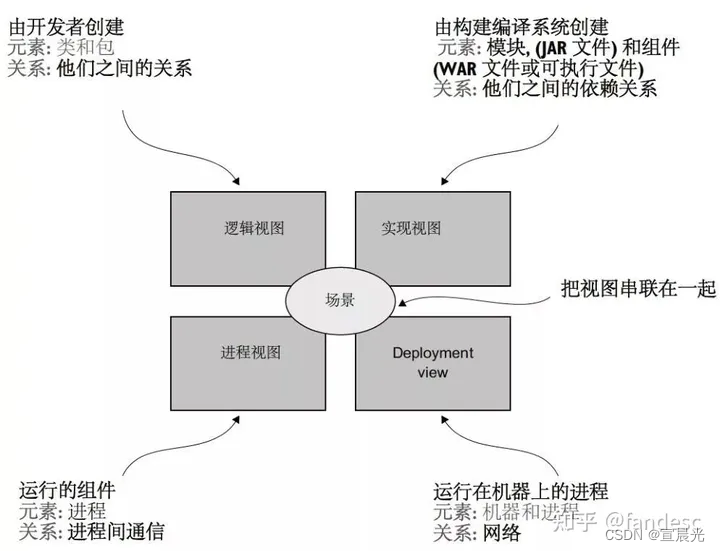
【软件架构】01-架构的概述
1、定义 软件架构就是软件的顶层结构 RUP(统一过程开发)4 1 视图 1)逻辑视图: 描述系统的功能、组件和它们之间的关系。它主要关注系统的静态结构,包括类、接口、包、模块等,并用于表示系统的组织结构…...

Vue 图片轮播第三方库 介绍
Vue图片轮播是一种在网页上以自动或手动方式展示图片的组件,常用于产品展示、网站banner等场景。有许多第三方库可以帮助Vue开发者轻松实现图片轮播功能。以下是一些流行的Vue图片轮播第三方库的介绍: 1. Vue-awesome-swiper - **简介**:V…...

设置主从复制时发生报错Could not find first log file name in binary log index file‘;解决方案
如图所示,slave_io_runnind:no,slave_sql_running:yes 此时,主从配置错误,我们可以查看Last_IO_Error:来查看报错信息 此时,我们需要停止从服务器的主从服务, mysql> stop slave; Query OK, 0 rows affected, 1 w…...

React Context的使用方法
背景:在某些场景下,你想在整个组件树中传递数据,但却不想手动地在每一层传递属性,你可以直接在React中使用强大的contextAPI 解决上述问题 在一个典型的React 中,数据通过Props属性自下而上(由父及子&…...

ElasticSearch索引数据备份与恢复
索引数据备份 在磁盘创建备份目录并授权 # 创建备份目录 /home/esbackup # 授权 chmod 777 /home/esbackup修改配置文件elasticsearch.yml echo path.repo: ["/home/esbackup"] >> /etc/elasticsearch/elasticsearch.yml重启elasticsearch(我是docker创建的…...

kubernetes日志收集 fluent-operator 动态索引名的实现
文章目录 按照服务名区分索引名1.修改fluent-operator,让其支持logstash_prefix_key2.让它能获取app name作为服务名3. 拼接索引名4. 应用变更 发自个人博客: https://uublog.com/article/20230510/kubernetes-fluent-operator-dynamic-index-name/ 日志…...

pip换源
windows环境下: 比如windows账号是 admin 那么建立 admin主目录下的 pip子目录,在此pip子目录下建立pip的配置文件:pip.ini c:\users\admin\pip\pip.ini # coding: GBK [global] index-url https://pypi.tuna.tsinghua.edu.cn/simple [ins…...

7.(数据结构)堆
7.1 相关概念 堆(Heap)在计算机科学中是一种特殊的数据结构,它通常被实现为一个可以看作完全二叉树的数组对象。以下是一些关于堆的基本概念: 数据结构: 堆是一个优先队列的抽象数据类型实现,通过完全二叉树…...

AWS Elastic Beanstalk通过应用负载均衡配置https
接上一篇,今天说说怎么通过AWS Elastic Beanstalk提供的应用负载均衡配置https。 首先创建应用和环境,这里应用可以使用上一篇文章中使用的demo应用(只需要package.json和app.js文件) 创建环境的时候,确认下面两个参…...

AC自动机:文本搜索的加速器
在数字化时代,文本数据的海洋浩瀚无垠。我们经常需要在这些数据中迅速找到特定的信息,比如在日志文件中查找异常、在海量文本中检索关键词,或是在编译代码时识别语法结构。这时候,AC自动机(Aho-Corasick自动机…...

备战蓝桥杯---基础算法刷题1
最近在忙学校官网上的题,就借此记录分享一下有价值的题: 1.注意枚举角度 如果我们就对于不同的k常规的枚举,复杂度直接炸了。 于是我们考虑换一个角度,我们不妨从1开始枚举因子,我们记录下他的倍数的个数sum个&#…...

探索 Flutter 中的动画:使用 flutter_animate
在移动应用开发中,动画是提升用户体验和吸引用户注意力的关键要素之一。Flutter 作为一种跨平台的移动应用开发框架,提供了丰富而灵活的动画支持。其中,flutter_animate 是一个强大的库,它为 Flutter 开发者提供了简单易用的方式来…...

装机容量对光伏发电量的影响有多大?如何通过装机容量计算发电量?
光伏行业得益于全球对环保和可持续发展的重视,得到了快速的发展。众所周知,光伏电站的收益受发电量的影响,发电量越大收益越高,但发电量其实受装机容量的影响。 一、装机容量对发电量的影响 光伏发电的核心就是发电板࿰…...

软考37-上午题-【数据库】-数据模型、数据库的三级模式和二级映像
一、考情简介 上午题:6分——6道选择题 下午题:15分——一道分析题 E-R图、关系模式:下午考试必考!!!(编制也要考!) 二、数据模型 数据模型是对现实世界数据特征的抽象…...
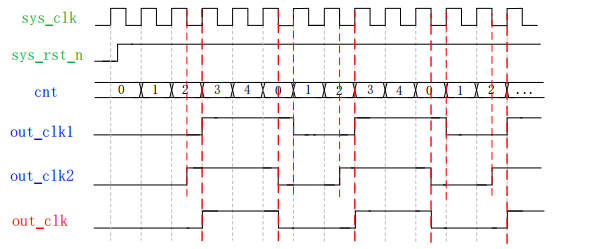
06 分频器设计
分频器简介 实现分频一般有两种方法,一种方法是直接使用 PLL 进行分频,比如在 FPGA 或者 ASIC 设计中,都可以直接使用 PLL 进行分频。但是这种分频有时候受限于 PLL 本身的特性,无法得到频率很低的时钟信号,比如输入 …...

力扣hot100题解(python版7-9题)
7、接雨水 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
