Toponogov 比较定理及其应用
1. Toponogov 比较定理的背景来源
Victor Andreevich Toponogov(1930-2004) 是苏联数学家,Toponogov 比较定理是他的博士论文题目,在1958年答辩。他证明这个定理是为了用于证明截面曲率假设下的分裂定理和最大直径定理,这两个定理后来都被推广到了只需要里奇曲率的假设。Berger 首先在证明 14\frac{1}{4}41-pinched sphere theorem 中用到了 Toponogov 比较定理,后来和 Grove Shiohama 的 Critical point theorem 被 Gromov 一起用来估计非负截面曲率流形的 Betti 数的估计。
2. 定理叙述及其几何理解
以下内容,我主要参考教材: Cheeger & Ebin 的 Comparison Theorems in Riemannian Geometry 以及上课的笔记。
首先我们定义测地三角形,这是欧氏空间里三角形的推广:
定义2.1 (测地三角形)黎曼流形 MnM^nMn 上的一个测地三角形,是一个集合,它由三个顶点 A,B,CA, B, CA,B,C 和三条分别连接两个不同顶点、首尾相接、具有单位速度的最短测地线段构成,用 ΔABC\Delta ABCΔABC 表示。
三角形各顶点各边的记号如下图所示:

注意这里定义,教材中要求两边之和大于第三边,而不要求最短测地线;有的教科书则直接要求最短测地线,比如 Petersen 的黎曼几何,其后面注释也有提到,其实证明中只要求在空间形式上对应的测地线是最短的。如 Petersen 上面的证明,这个定理也可以从方程的角度,比如用所谓的 RiccatiRiccatiRiccati 比较来证明。
三角形去掉一边,定义为铰链(Hinge):
定义2.2 (铰链)由流形上一点 AAA 和两条最短测地线 γ1,γ2\gamma_1, \gamma_2γ1,γ2 构成,γ1(l1)=γ2(0)=A\gamma_1(l_1)=\gamma_2(0)=Aγ1(l1)=γ2(0)=A,角度记为 α\alphaα. 用 (A,γ1,γ2)(A, \gamma_1, \gamma_2)(A,γ1,γ2) 表示。

铰链就长这样↑
定理2.3 (Toponogov)(Mn,g)(M^n, g)(Mn,g) 是一个完备黎曼流形,其截面曲率 KM≥H,HK_M\geq H, HKM≥H,H 是某个固定常数,M‾\underline{M}M 是二维常截面曲率 HHH 的空间形式,则:
(i)(三角形比较)∀ΔABC⊂M,∃\forall \Delta ABC\subset M, \exist∀ΔABC⊂M,∃ 比较三角形 ΔABC‾⊂M‾\Delta \underline{ABC}\subset \underline{M}ΔABC⊂M, 使得二者边长对应相等,角度满足:
α‾≤α,β‾≤β,γ‾≤γ.\underline{\alpha}\leq\alpha, \underline{\beta}\leq\beta, \underline{\gamma}\leq\gamma.α≤α,β≤β,γ≤γ.并且比较三角形在合同变换的意义下唯一(除了H>0H>0H>0,且存在一条边的长度等于空间形式的直径时);
(ii)(铰链比较)∀(A,γ1,γ2)⊂M,∃\forall (A, \gamma_1, \gamma_2)\subset M, \exist∀(A,γ1,γ2)⊂M,∃ 比较铰链 (A‾,γ1‾,γ2‾)⊂M‾(\underline{A}, \underline{\gamma_1}, \underline{\gamma_2})\subset\underline{M}(A,γ1,γ2)⊂M,使得 d(γ1(0),γ2(l2))≤d‾(γ1‾(0),γ2‾(l2)).d(\gamma_1(0), \gamma_2(l_2))\leq\underline{d}(\underline{\gamma_1}(0), \underline{\gamma_2}(l_2)).d(γ1(0),γ2(l2))≤d(γ1(0),γ2(l2)).
定理2.3的(i)说明较大曲率流形上的三角形,和二维空间形式上的三角形相比,边长相等时,曲率大则角度也大。比方说我们比较球面和欧氏空间上的三角形,由高斯博内公式可知,球面上三角形的内角和大于 π\piπ;比较欧氏空间和双曲空间,同样可知双曲空间上三角形的内角和小于 π\piπ,这也符合Toponogov比较定理。直观上来看,球面上的三角形更“胖”,双曲空间上的三角形更“瘦”。更近一步,Toponogov比较定理说大曲率流形上三角形的每个角都更大。
3. 证明概叙
首先我们考虑曲率为 H−ϵH-\epsilonH−ϵ 的空间形式,原因在我的理解里有两个:
其一是此时排除了一条边长度等于球面经线长度的情况,使得比较三角形在合同的意义下唯一;
其二是在证明(5)(6)(7)步中,要对瘦的(Thin)铰链证明时,需要保证沿着一条边,每个点的单射半径有大于零的下界(即书中要求沿着一条边没有 focal point)。
证明分为 101010 步:
(1)对空间形式上的铰链而言,所去除那条边的长度,随铰链的角度 α‾\underline{\alpha}α 严格单调递增,并且长度有上下界:
证明可以用第一变分公式(Cheeger&Ebin),对一组测地线变分,变分公式中的积分项为 000,只剩边界项在一边端点取值;
也可以用空间形式上的余弦定理(Petersen)直接得到。
(2)证明比较三角形在合同变换(Congruence)下的唯一性:
因为空间形式具有齐性,任意两点可以通过空间形式的等距映射对应起来,这样对应了三角形的第一个点,第二个点根据长度相等也被固定,第三个点之间至多相差一个反射。
(3)证明定理叙述(i)中三角形的比较等价于(ii)中铰链的比较:
这一步主要用到单调性,分别画出流形和空间形式上的三角形和铰链,绕两下就可以比较出来。
这样我们接下来的步骤只需要对铰链证明即可。
(4)证明对于小的(Small)铰链,结论(ii)成立:
所谓小的铰链 (A,γ1,γ2)(A, \gamma_1, \gamma_2)(A,γ1,γ2),是指两条边的长度都小于顶点单射半径的一半:
L(γi)<12injA,i=1,2.L(\gamma_i)<\frac{1}{2}\text{inj}_A, \quad i=1,2.L(γi)<21injA,i=1,2.这样确保了连成三角形后,第三条边同样在顶点的单射半径里。“小的”三角形也是类似的定义,三角形分别除去一条边得到的三个铰链,都是小的。
这一步是我觉得最有意思的一步,别的步骤是进行转化、剖分、归纳之类的操作,这一步要用到之前所讲的 Rauch 比较定理的第二个版本:
先在空间形式上用最短测地线 γ‾(t)\underline{\gamma}(t)γ(t)连接铰链,将这条最短测地线通过指数映射拉回到 A‾\underline{A}A 的切空间中,得到曲线 c‾(t)\underline{c}(t)c(t),通过等距嵌入,c‾(t)\underline{c}(t)c(t)对应到流形上 AAA 点处的切空间里的曲线 c(t)c(t)c(t),注意这时 expA(c(t))\text{exp}_A(c(t))expA(c(t)) 并不一定是连接流形上铰链的测地线;
有了这两条曲线,我们可以得到流形和空间形式上的两族测地线的变分,验证他们满足 Rauch 比较定理的条件,可以得到他们在端点处的变分向量场的比较,从而得到曲线长度的比较 L(γ‾)≥L(γ)L(\underline{\gamma})\geq L(\gamma)L(γ)≥L(γ),因为 γ\gammaγ 并不一定是最短测地线,所以有结论成立。

(5)证明对瘦的(Thin)直角铰链(ii)成立:
空间形式中的铰链用最短测地线连接斜边,再像第(4)步一样,瞄准 Rauch 比较定理的条件,构造垂直一边的平行单位向量场,然后写出变分,照搬到原先的流形 MMM 上,这时流形上连接铰链的曲线由空间形式上搬过来,不一定是最短测地线。
所谓瘦的直角铰链,就是指对流形中的图形,选定的那条边没有 focal point(有点拗口),看下方图形很直观可以理解。
这样就可以应用 Rauch 比较定理得出结论。
(6)证明对瘦的钝角铰链(ii)成立:
从空间形式出发,将用最短测地线连接的铰链剖分成直角三角形和一个新的钝角三角形,对钝角铰链而言,“瘦”是指剖分后,得到一个瘦的直角三角形和一个“小”的三角形。

(7)证明对瘦的锐角铰链(ii)成立:
如下图,瘦的锐角铰链是指,用最短测地线连接后,从一个铰链的“脚”向内做垂线,会得到一个小的三角形和一个瘦的直角三角形。
我们先比较小三角形,再比较剩余部分就可以得到结论。
(8)(9)证明对一般铰链(ii)成立:
将一般的三角形剖分成充分瘦的三角形,再用归纳法。
(10)令 ϵ→0\epsilon\rightarrow0ϵ→0即可。
4. Toponogov 比较定理的应用
4.1 Petersen书中的介绍
这里只能粗略的介绍,Petersen 的黎曼几何(第三版)第12章介绍了很多应用,第12章的前言总结的很好,摘录在这里:
It wasn’t until Grove and Shiohama developed critical point theory to prove their diameter sphere theorem that Toponogov’s theorem was put to serious use. Shortly after that, Gromov put these two ideas to even more nontrivial use, with his Betti number estimate for manifolds with nonnegative sectional curvature. After that, it became clear that in working with manifolds that have lower sectional curvature bounds, the two key techniques are Toponogov’s theorem and the critical point theory of Grove-Shiohama.
正文中的内容这里只取前两个:
1.1.1. Rauch-Berger-Klingenberg sphere theorem, 或者 14\frac{1}{4}41-pinched sphere theorem.
定理4.1.1(14\frac{1}{4}41-Pinched Shpere Theorem)对于一个单连通闭的黎曼流形 (Mn,g)(M^n,g)(Mn,g),如果截面曲率满足 secM∈(1,4]sec_M\in(1,4]secM∈(1,4],则 MMM 同胚于 SnS^nSn.
2.2.2. Soul Theorem.
定理4.1.2 (Soul Theorem)如果完备非紧的黎曼流形(M,g)(M,g)(M,g) 满足截面曲率 secM≥0sec_M\geq0secM≥0,则 MMM 包含一个灵魂 SSS,它是一个闭的全凸子流形,并且 MMM 微分同胚于底流形为 SSS 的某个法丛。更进一步,如果 MMM 的截面曲率处处为正,则灵魂 SSS 是一个点,因此MMM 微分同胚于 Rn\mathbb{R}^nRn.
这个定理的证明想法我曾在去年(2022年)戎老师度量黎曼几何的期末口试上讲过。后来 Cheeger 猜想只需要在一点处截面曲率全为正的,就能推出流形的灵魂是一个点,被称为灵魂猜想。这个猜想的证明是佩雷尔曼的“成名作”,证明只有两页。
后续还提及了有限性定理等等,这里就不说了(主要还没学会)。
4.2 Alexandrov空间
如课上所讲,Toponogov 比较定理在 Alexandrov 空间中是类似公理的内容,所谓的 CAT(k)CAT(k)CAT(k) 空间,其中 T 就代表着 Toponogov,事实上 Toponogov 和 Alexandrov 两人也互相影响(这块东西我也是一窍不通)。
参考文献:
[1] 课程笔记;
[2] Peter Petersen. Riemannian Geometry, 3rd edn;
[3] Cheeger, Ebin, Comparison Theorems in Riemannian Geometry.
[4] Toponogov 的遗产:http://www.pdmi.ras.ru/EIMI/2020/GL/toponogov.html
相关文章:

Toponogov 比较定理及其应用
1. Toponogov 比较定理的背景来源 Victor Andreevich Toponogov(1930-2004) 是苏联数学家,Toponogov 比较定理是他的博士论文题目,在1958年答辩。他证明这个定理是为了用于证明截面曲率假设下的分裂定理和最大直径定理࿰…...

力扣sql简单篇练习(二十二)
力扣sql简单篇练习(二十二) 1 上月播放的儿童适宜电影 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 a 示例输入 b 示例输出 1.2 示例sql语句 # Write your MySQL query statement belowSELECT titleFROM ContentWHERE kids_contentY AND content_typeMoviesAND c…...

【开源硬件】STM32F030R8T6系统板
【开源硬件】STM32F030R8T6系统板✅STM32F030R8T6系统板兼容极海APM32F030R8T6 🔰支持stm32cubemx工程配置成STM32F030R8T6生成的MDK工程,经过Keil编译后可以直接使用ST-Link v2烧录器上传到极海APM32F030R8T6芯片当中,完全做到平替使用&…...
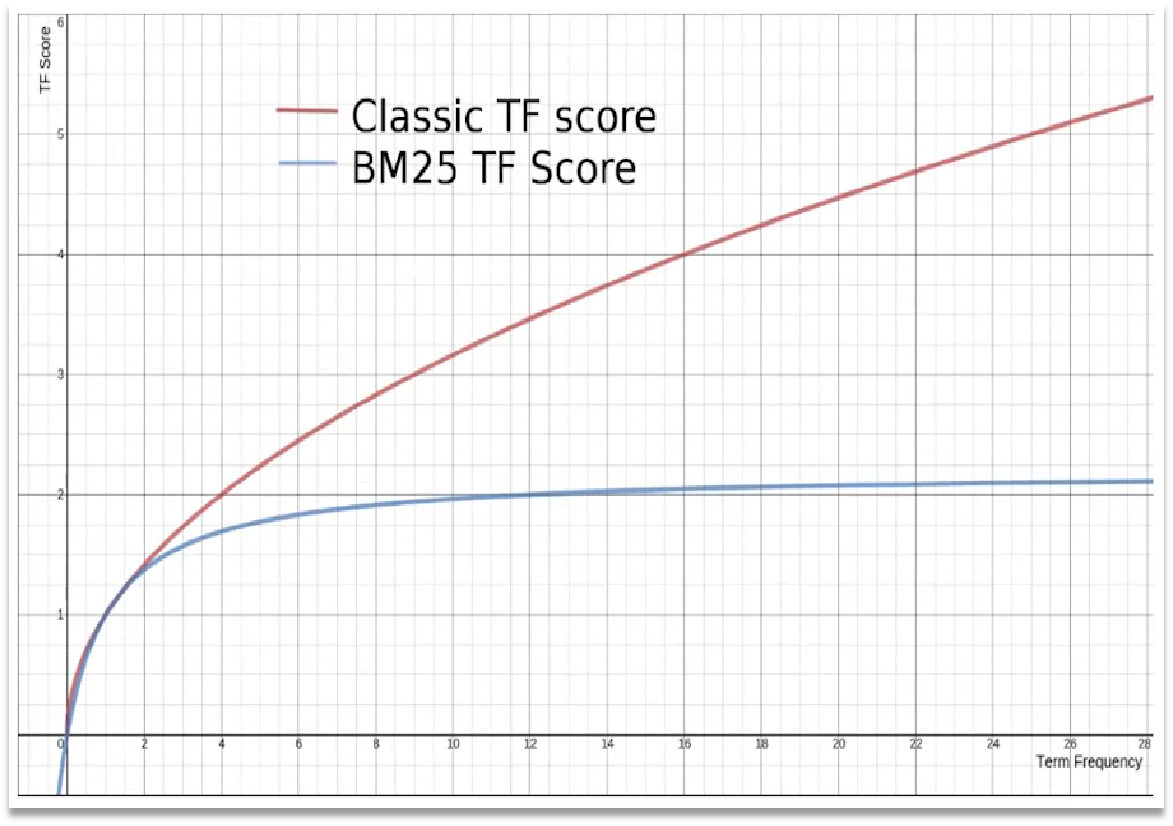
ES之DSL查询文档基础查询
分类 query查询分类 总体规律就是逻辑性的,从外层的你干嘛,到下一层的查询类型,再到下一层的查询字段(如果需要的话)和然后是查询内容 查询所有 语法 get /索引库名/_serarch {"query":{"查询条件…...

数据结构与算法之堆排序
目录堆排序概述代码实现时间复杂度堆排序概述 堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点…...

Vue3 中的模板语法
目录前言一、什么是模板语法?二、内容渲染指令1. v-text2. {{ }} 插值表达式3. v-html三、双向绑定指令1. v-model2. v-model的修饰符四、属性绑定指令1. 动态绑定多个属性值2. 绑定class和style属性五、条件渲染指令1. v-if、v-else-if、v-else2. v-show3. v-if和v…...

Redis十大类型——Hash常见操作
Redis十大类型——Hash常见操作命令操作简列存放及获取获取健值对长度元素查找列出健值对对数字进行操作赋值hsetnx很明显咯它也是以健值对方式存在的,只不过value也就是值,在这里也变成了一组简直对。 🍊个🌰: 想必多…...

Python采集本地二手房,一键知晓上万房源信息
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 所以今天教大家用Python来采集本地房源数据,帮助大家筛选好房。 话不多说,让我们开始愉快的旅程吧~ 更多精彩内容、资源皆可点击文章下方名片获取此处跳转 本文涉及知识点 采集基本流程 requests 发送…...

Ubuntu 18.04 出现GLIBC_2.28 not found的解决方法(亲测有效)
关于/lib/x86_64-linux-gnu/libc.so.6: version GLIBC_2.28’ not found出现报错,建议不要使用源码包去编译并升级。在下文有分享一个使用官方的Debian软件包去升级使用的方法。仅供参考! 环境 # uname -a Linux Ubuntu 5.4.0-144-generic #161~18.04.…...

Java文档搜索引擎总结
Java文档搜索引擎总结项目介绍项目使用的技术栈前端页面展示后端逻辑部分索引部分搜索模块部分Web模块部分项目介绍 Java文档搜索引擎项目是一个SSM项目,该项目的前端界面部分是由搜索页面和展示页面组成,后端部分索引模块(ScanAnalysis、in…...
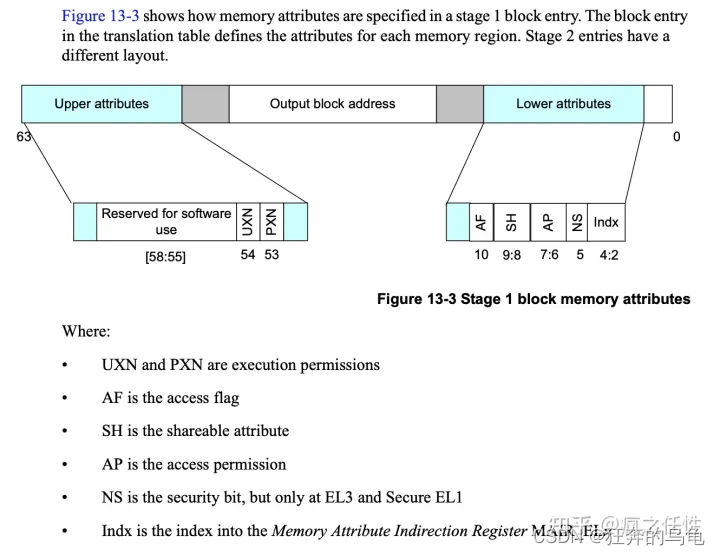
Linux内核学习笔记——页表的那些事。
目录页表什么时候创建内核页表变化什么时候更新到用户页表源码分析常见问题解答问题一:页表到底是保存在内核空间中还是用户空间中?问题2:页表访问,软件是不是会频繁陷入内核?问题3:内存申请,软…...

C++,Qt分别读写xml文件
XML语法 第一行是XML文档声明,<>内的代表是元素,基本语法如以下所示。C常见的是使用tiny库读写,Qt使用自带的库读写; <?xml version"1.0" encoding"utf-8" standalone"yes" ?> <根元素>…...
WebStorm安装教程【2023年最新版图解】一文教会你安装
文章目录引言一、下载WebStorm三、WebStorm激活配置及创建项目Active Code安装完成尝试新建一个项目引言 今天发现了一个专注前端开发的软件,相比VSCode的话,这个好像也不错,为了后续做个API接口项目做准备。 对于入门JavaScript 开发的者&am…...

用户态和内核态,系统调用
特权指令:具有特殊权限的指令,比如清内存,重置时钟,分配系统资源,修改用户的访问权限 由于这类指令的权限最大,所以使用不当会导致整个系统崩溃 系统调用:是操作系统提供给应用程序的接口(供应…...

Java 包装类
Java 中有些类只能操作对象,因此 Java 的基本数据类型都有一个对应的包装类。 byte:Byteshort:Shortint:Integerlong:Longfloat:Floatdouble:Doublechar:Characterbooleanÿ…...

Raspberry Pi GPIO入门指南
如果您想使用 Raspberry Pi 进行数字输入/输出操作,那么您需要使用 GPIO(通用输入/输出)引脚。在这篇文章中,我们将为您提供 Raspberry Pi GPIO 的基础知识,包括如何访问和操作 GPIO 引脚。 0.认识GPIO 树莓派上的那…...

汇编语言程序设计(三)之汇编程序
系列文章 汇编语言程序设计(一) 汇编语言程序设计(二)之寄存器 汇编程序 经过上述课程的学习,我们可以编写一个完整的程序了。这章开始我们将开始编写完整的汇编语言程序,用编译和连接程序将它们连接成可…...

用二极管和电容过滤电源波动,实现简单的稳压 - 小水泵升压改装方案
简而言之,就是类似采样保持电路,当电源电压因为电机启动而骤降时,用二极管避免电容电压跟着降低,从而让电容上连接的低功耗芯片有一个比较稳定的供电电压。没什么特别的用处,省个LDO 吧,电压跌幅太大的时候…...

【数据结构与算法】数据结构有哪些?算法有哪些?
1. 算法与数据结构总览图 2.常用的数据结构 2.1.数组(Array) 数组是一种聚合数据类型,它是将具有相同类型的若干变量有序地组织在一起的集合。数组可以说是最基本的数据结构,在各种编程语言中都有对应。一个数组可以分解为多个数…...
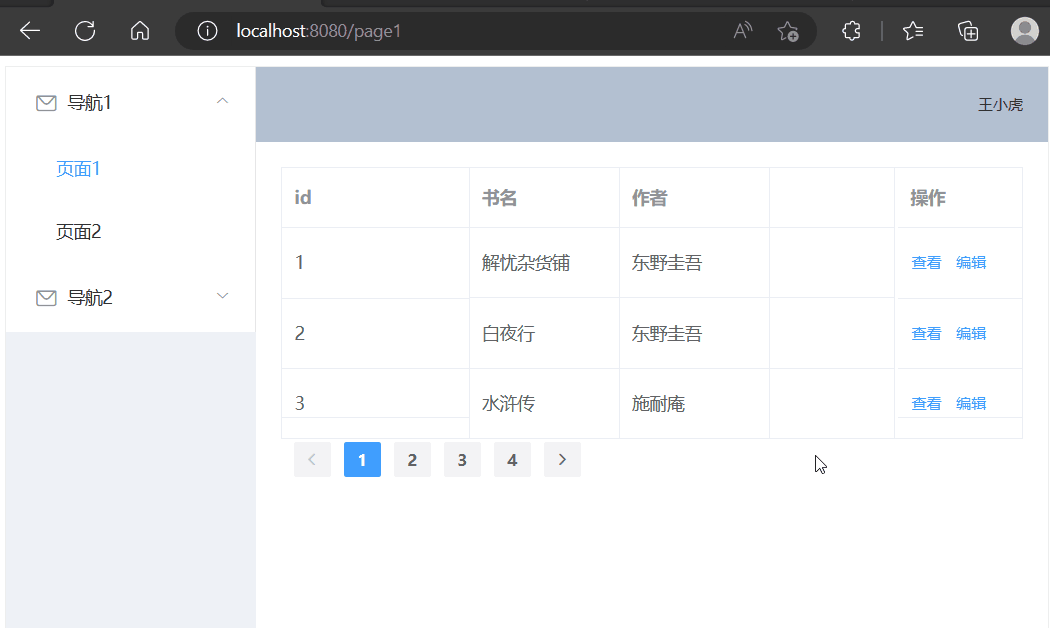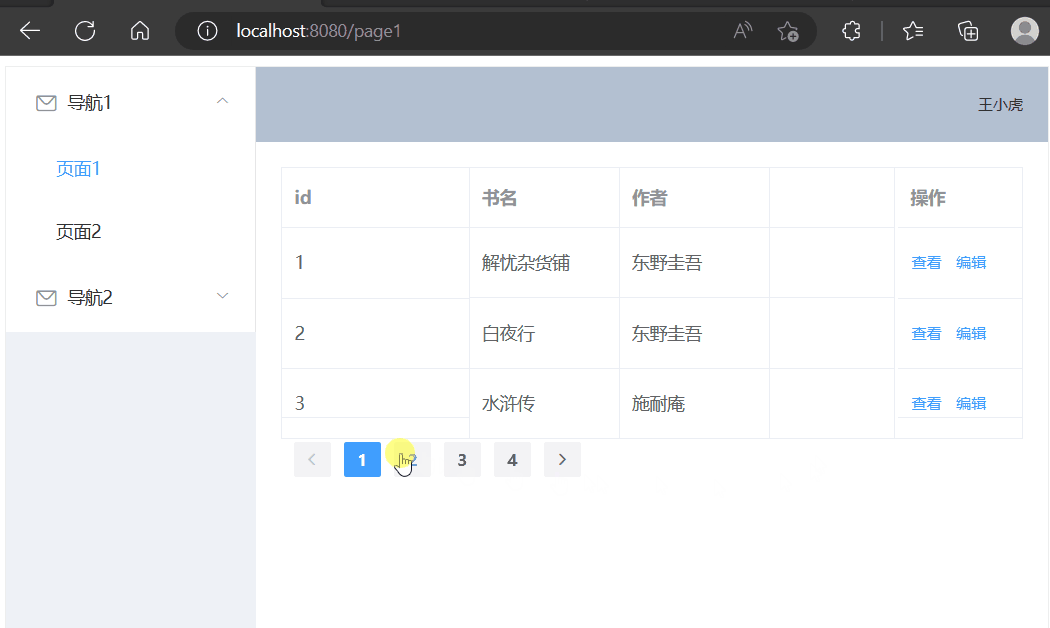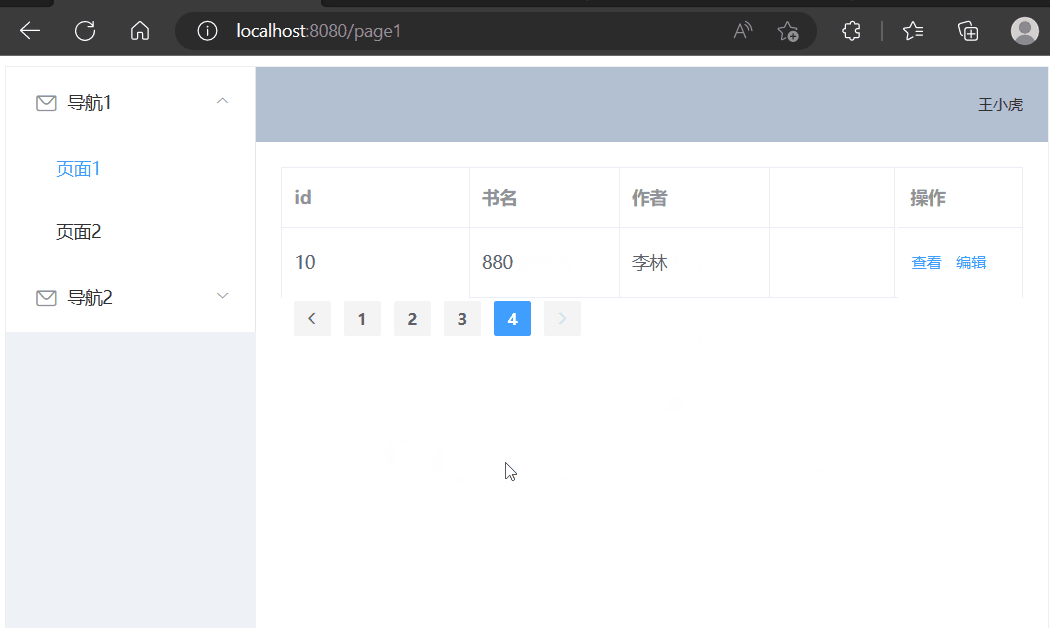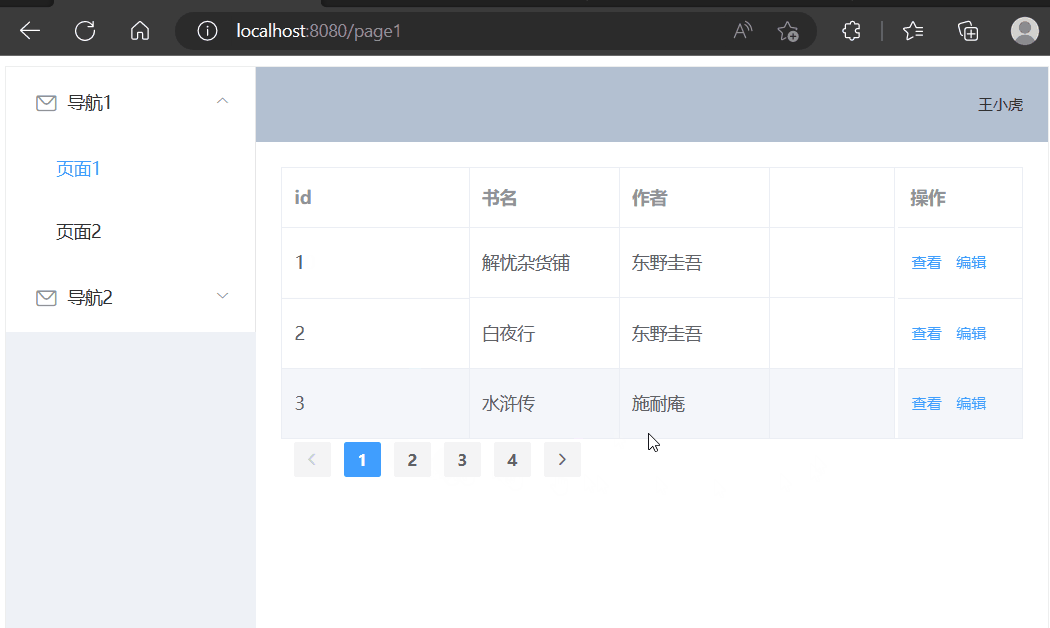
使用Element-UI展示数据(动态查询)
学习内容来源:视频P4 本篇文章进度接着之前的文章进行续写 精简前后端分离项目搭建 Vue基础容器使用 目录选择组件修改表格组件修改分页组件增加后端接口前端请求数据接口页面初始化请求数据点击页码请求数据选择组件 在官方文档中选择现成的组件,放在页…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
