神经网络系列---回归问题和分类问题
文章目录
- 回归问题和分类问题
- 回归问题:
- 分类问题:
- 多分类问题:
- 排序问题:
- 自定义损失函数:
回归问题和分类问题
回归问题:
回归问题是一种预测连续数值输出的任务。在这种问题中,模型的目标是根据输入特征预测出一个连续值。举例来说,回归问题可以包括预测房屋价格、销售量、温度、股票价格等。回归模型的输出是一个连续的实数或浮点数。
在回归问题中,我们需要训练模型使其学习从输入特征到输出连续值之间的映射关系。
为了评估回归模型的性能,通常使用各种评估指标,例如均方误差 (Mean Squared Error, MSE)、均方根误差 (Root Mean Squared Error, RMSE)、平均绝对误差 (Mean Absolute Error, MAE) 等。这些指标用于衡量模型的预测与真实连续标签之间的差异。
- 均方误差 (Mean Squared Error, MSE):适用于回归问题,衡量预测值与真实值之间的平方差异,定义为预测值与真实值之差的平方的均值。
- 平均绝对误差 (Mean Absolute Error, MAE):也适用于回归问题,衡量预测值与真实值之间的绝对差异,定义为预测值与真实值之差的绝对值的均值。
分类问题:
分类问题是一种预测离散标签或类别的任务。在分类问题中,模型的目标是将输入映射到预定义的类别或标签中。例如,将电子邮件分类为“垃圾邮件”或“非垃圾邮件”,将图像分类为“猫”或“狗”等。分类模型的输出是离散的类别。
分类问题可以进一步分为二分类和多分类。在二分类中,模型需要将输入分为两个类别,而在多分类中,模型需要将输入分为多个类别。
- 交叉熵损失函数 (Cross-Entropy Loss):适用于二分类问题,特别是在使用逻辑回归或神经网络进行二分类时。它度量预测概率与真实标签之间的差异。常见的交叉熵损失函数有二元交叉熵损失 (Binary Cross-Entropy Loss) 和对数损失 (Log Loss)。
总结:
- 回归问题用于预测连续数值输出。
- 分类问题用于预测离散标签或类别输出。
- 回归问题的输出是连续值,分类问题的输出是离散类别。
- 回归问题使用不同的评估指标(例如MSE、RMSE),而分类问题使用准确率、精确率、召回率等指标。
在机器学习中,选择适当的损失函数是非常重要的,它直接影响到模型的训练和性能。损失函数用于度量模型的预测与真实标签之间的差异,模型的目标是通过最小化损失函数来提高预测的准确性。下面是一些常见的损失函数,它们适用于不同类型的任务:
多分类问题:
- 交叉熵损失函数 (Cross-Entropy Loss):同样适用于多分类问题。在多分类中,交叉熵损失函数用于度量预测的概率分布与真实标签的分布之间的差异。常见的多分类交叉熵损失函数有分类交叉熵损失 (Categorical Cross-Entropy Loss) 和稀疏分类交叉熵损失 (Sparse Categorical Cross-Entropy Loss)。
排序问题:
- 排序损失函数 (Ranking Loss):适用于排序问题,例如在搜索引擎中优化搜索结果的排序。常见的排序损失函数有排名SVM损失和排序的softmax损失。
自定义损失函数:
- 在某些情况下,特定任务可能需要定制的损失函数。根据任务的需求,可以定义适合特定问题的损失函数。
相关文章:

神经网络系列---回归问题和分类问题
文章目录 回归问题和分类问题回归问题:分类问题:多分类问题:排序问题:自定义损失函数: 回归问题和分类问题 回归问题: 回归问题是一种预测连续数值输出的任务。在这种问题中,模型的目标是根据…...

Jetpack Compose 与 Kotlin 的兼容性对应关系
点击查看:Jetpack Compose 教程 点击查看:Jetpack Compose Kotlin 的兼容性 官网 声明依赖项 如需添加 Compose Compiler 的依赖项,您必须将 Google Maven 代码库添加到项目中。如需了解详情,请参阅 Google 的 Maven 代码库。 …...

汇编反外挂
在软件保护领域,尤其是游戏保护中,反外挂是一个重要的议题。外挂通常指的是一种第三方软件,它可以修改游戏数据、操作游戏内存或提供其他作弊功能,从而给玩家带来不公平的优势。为了打击外挂,游戏开发者会采取一系列措…...

134 Linux 系统编程11 ,readlink命令,文件目录rwx权限差异,目录操作函数
一 readlink 命令 前面知道,如果a.soft是一个软链接,我们使用 cat a.soft,会直接查看这个软链接指向的文件 那么我们就是想看这个软链接是啥,可以使用 readlink a.soft 二 获取工作目录 getcwd函数 获取进程当前工作目录 (卷3,标…...
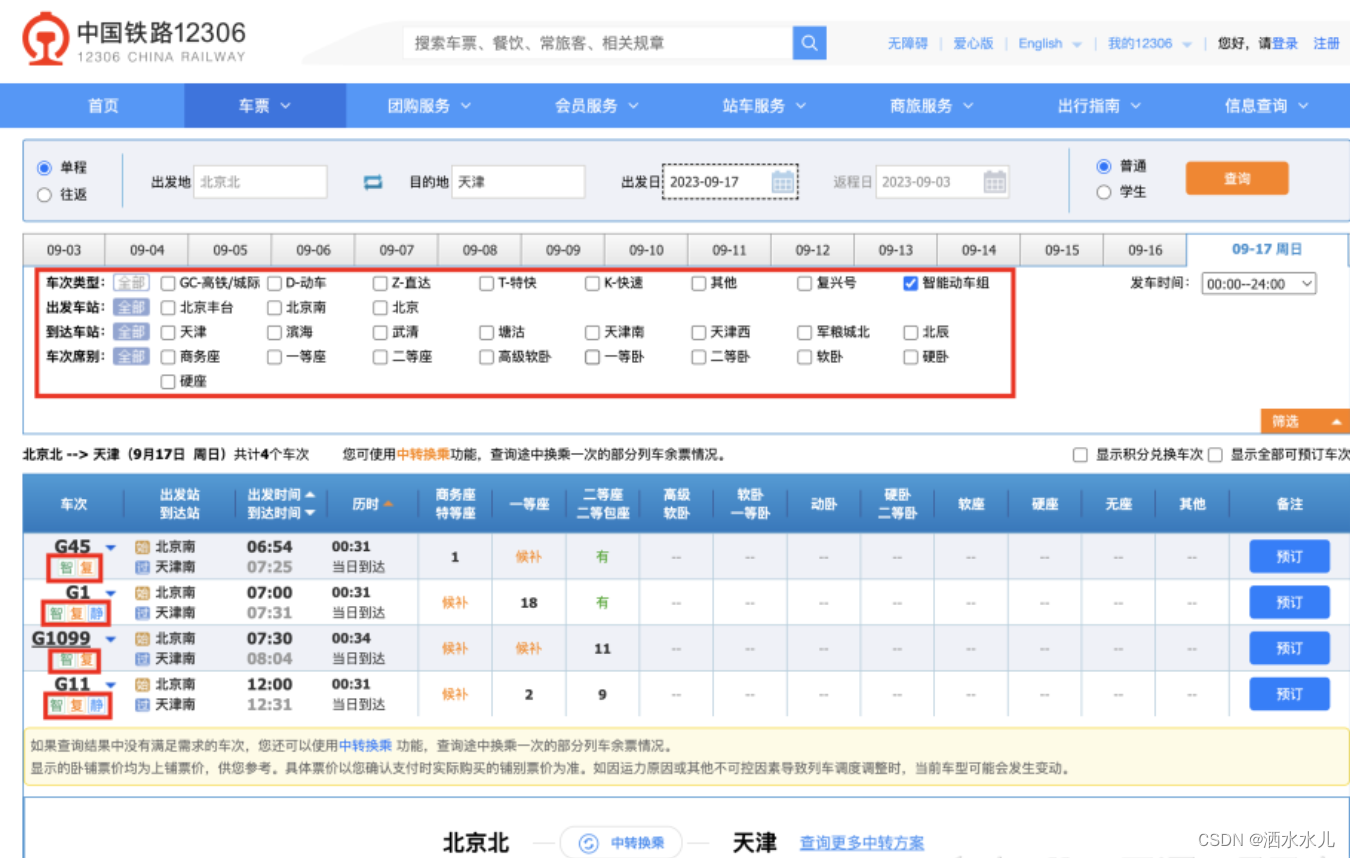
仿12306校招项目业务二(列车检索)
目录 验证数据 加载城市数据 查询列车站点信息 查询列车余票信息 构建列车返回数据 12306 项目中列车数据检索接口路径  TicketController的pageListTicketQuery。 GetMapping("/api/ticket-service/ticket/query")public Result<T…...

前端架构: 实现脚手架终端UI样式之ANSI escape code, Chalk, Ora介绍
在脚手架当中实现命令行的UI显示 1 )概述 在命令行中,如果想实现除传统的常规文本以外的内容比如想对字体进行加粗斜体下划线,包括对它改变颜色改变前景色改变后景色等等需要借助一个叫做 ANSI escape code 这样的一个概念它其实是一个标准&…...

platform(驱动层+应用层)实现终端和中断开关点灯
设备树文件添加 myplatform{compatible"hqyj,myplatform";interrupt-parent<&gpiof>;interrupts<8 0>,<7 0>,<9 0>;led1-gpio<&gpioe 10 0>;led2-gpio<&gpiof 10 0>;led3-gpio<&gpioe 8 0>;reg<0x123…...
黑马JavaWeb开发跟学(一)Web前端开发HTML、CSS基础
黑马JavaWeb开发一.Web前端开发HTML、CSS基础 引子、Web开发介绍传统路线本课程全新路线本课程适用人群课程收获一、什么是web开发二、网站的工作流程三、网站的开发模式四、网站的开发技术 前端开发基础一、前端开发二、HTML & CSS2.1 HTML快速入门2.1.1 操作第一步第二步…...
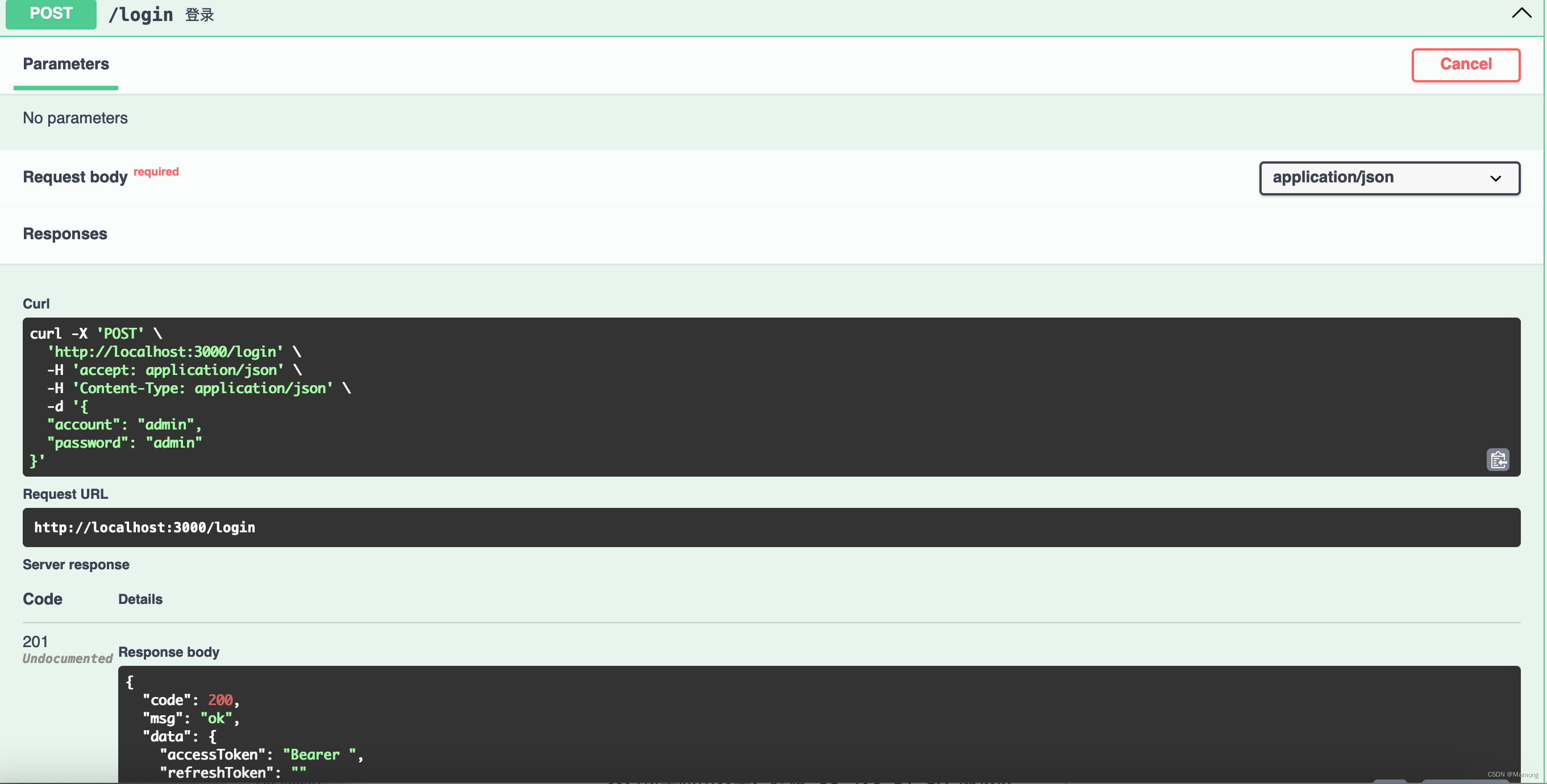
Nest.js权限管理系统开发(四)Swagger API接入
什么是swagger Swagger 是一个规范和完整的框架,用于生成、描述、调用和可视化 RESTful 风格的 Web 服务(<https://swagger.io/>)。 它的主要作用是: 1. 使得前后端分离开发更加方便,有利于团队协作 2. 接口的文档在线自动生成…...
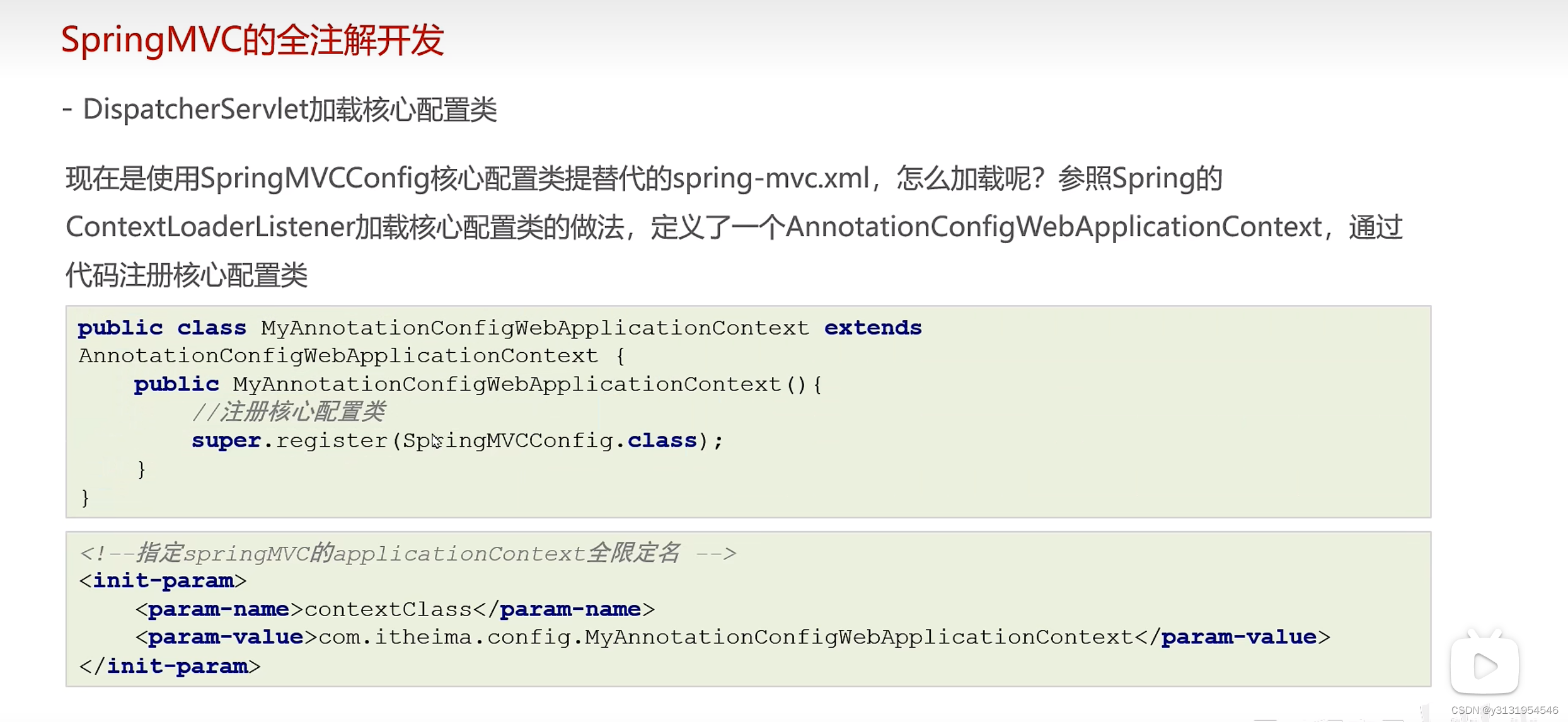
(全注解开发)学习Spring-MVC的第三天
全注解开发 第一部分 : 1.1 消除spring-mvc.xml 这些是原来spring-mvc.xml配置文件的内容 <!--1、组件扫描, 使Controller可以被扫描到--><context:component-scan base-package"com.itheima.controller"/><!--2、非自定义的Bean, 文件上传解析器--&…...
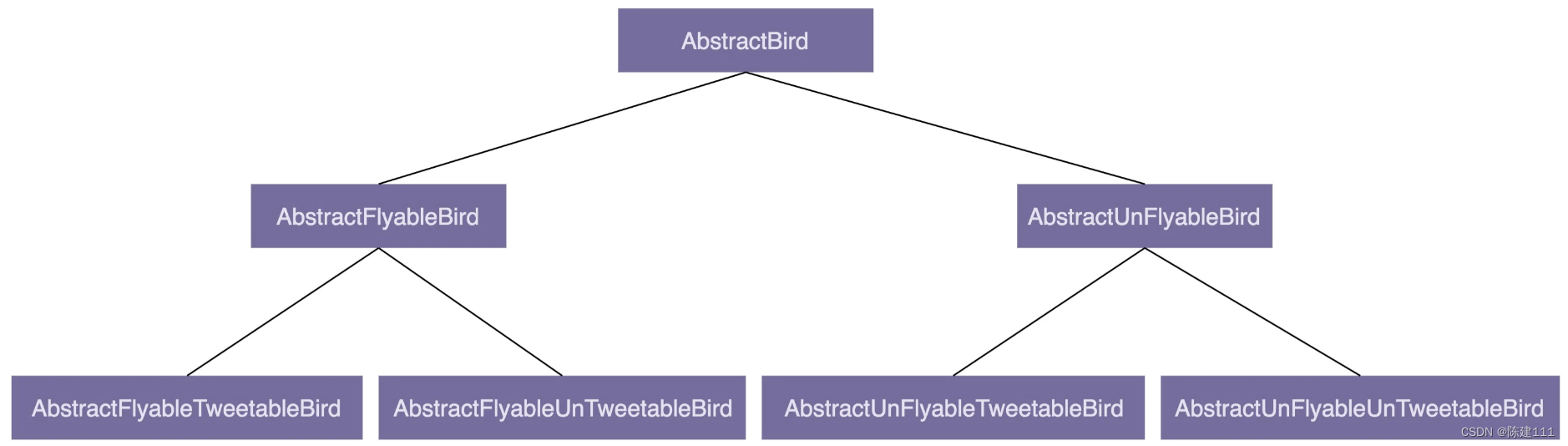
设计模式学习笔记 - 面向对象 - 7.为什么要多用组合少用继承?如何决定该用组合还是继承?
前言 在面向对象编程中,有一条非常经典的设计原则:组合优于继承,多用组合少用继承。 为什么不推荐使用继承? 组合比继承有哪些优势? 如何判断该用组合还是继承? 为什么不推荐使用继承? 继承…...
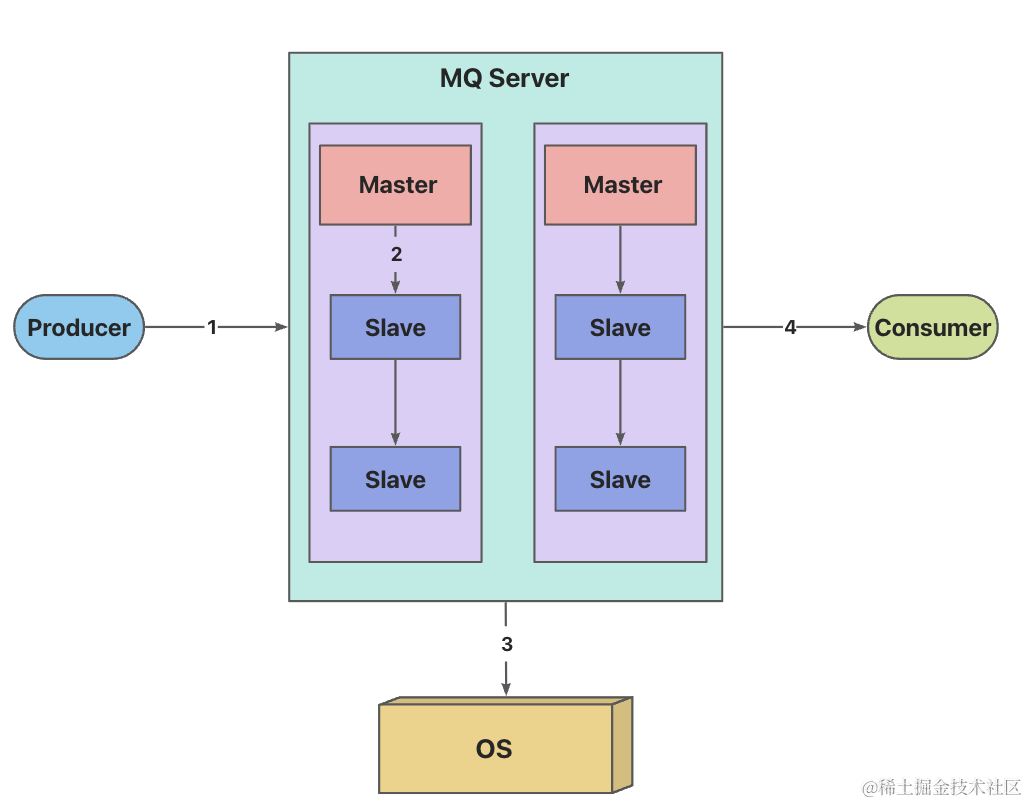
RocketMQ生产环境常见问题分析与总结
RocketMQ生产环境常见问题分析与总结 如何保证消息不丢失 消息丢失场景 对于跨网络的节点可能会丢消息,因为MQ存盘都会先写入OS的PageCache中,然后再让OS进行异步刷盘,如果缓存中的数据未及时写入硬盘就会导致消息丢失 生产端到Broker端Brok…...
)
前端打包工具的发展历程、思路(grunt,gulp,webpack,vite)
现在前端发展真快,需要学的东西太多了,下面总结下前端打包的发展过程,便于区分和选择学习。 什么是前端打包 前端打包是指将多个JavaScript文件、CSS文件、图片等资源进行合并和优化处理,并输出为一个或多个文件的过程。这样做的目的是减少…...
)
利用Python将文件夹下多个txt文本写入到同一个excel中(每一个文件占一行)
1、 将文件夹下多个txt文本写入到同一个excel中(每一个文件占一行): # -*- coding: utf-8 -*- import os import pandas as pd# 获取文件夹中的所有txt文件 folder_path rG:\Cygwin\ txt_files [f for f in os.listdir(folder_path) if f.endswith(.t…...

通过Colab部署Google最新发布的Gemma模型
Gemma的简单介绍 Gemma 是一系列轻量级、最先进的开放式模型,采用与创建 Gemini 模型相同的研究和技术而构建。 Gemma 由 Google DeepMind 和 Google 的其他团队开发,其灵感来自 Gemini,其名称反映了拉丁语 gemma,意思是“宝石”…...

spring中@validate注解使用
在 Java 中,我们可以使用注解和 validate 实现对实体类中字段的校验。其中,注解用来定义字段的约束条件,而 validate 则用来进行实际的校验操作。 常用的校验注解包括 NotNull、NotEmpty、Size、Min、Max 等,它们可以帮助我们规定…...
)
停车场管理(C语言)
【题目描述】停车场管理。设有一个可以停放n辆汽车的狭长停车场,它只有一个大门可以供车辆进出。车辆按到达停车场时间的先后次序依次从停车场最里面向大门口处停放 (即最先到达的第一辆车停放在停车场的最里面) 。如果停车场已放满n辆车,则以后到达的车…...

探索无限:Sora与AI视频模型的技术革命 - 开创未来视觉艺术的新篇章
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua,在这里我会分享我的知识和经验。&#x…...
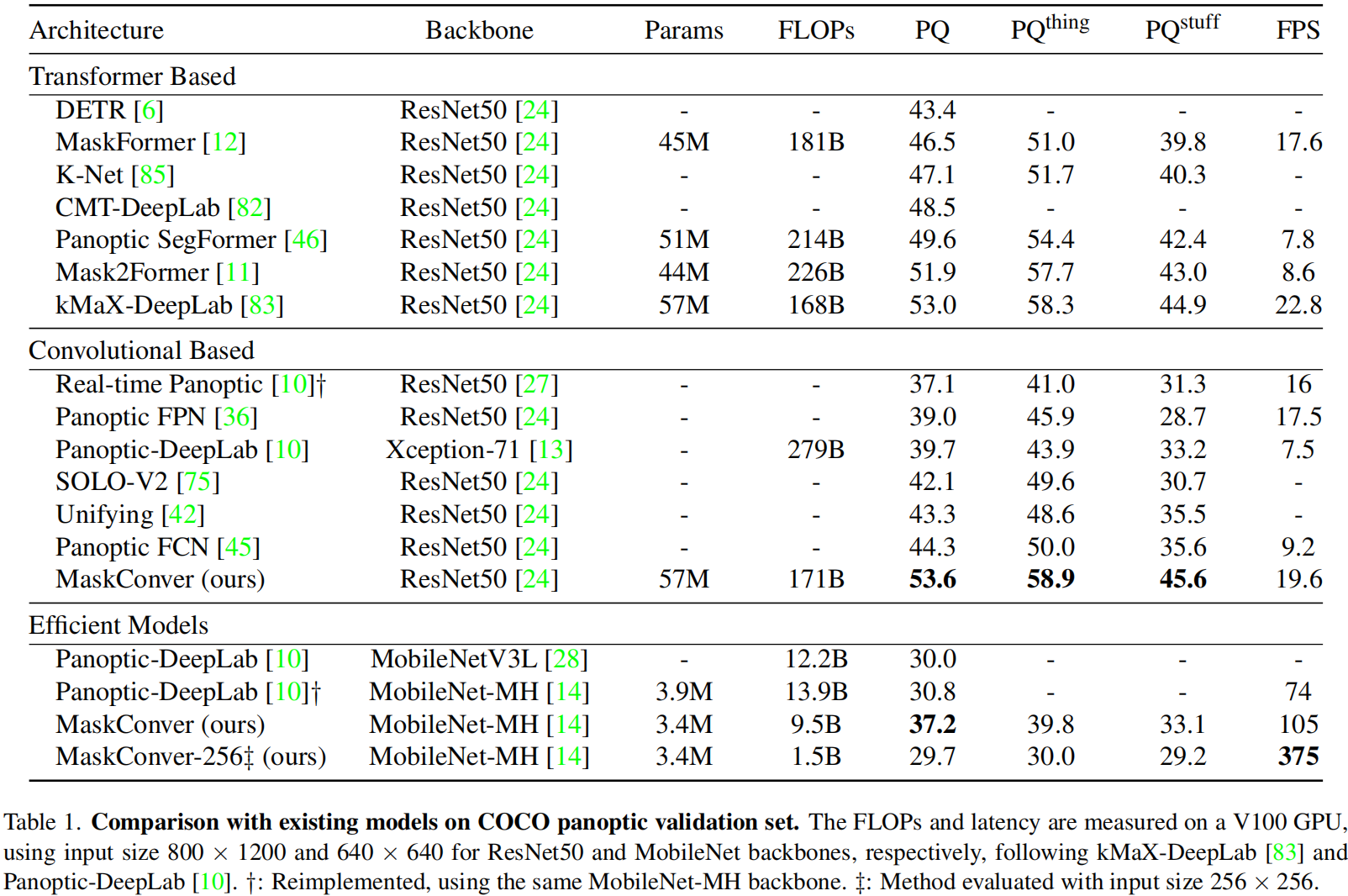
375FPS! 谷歌提出MaskConver“重校正用于全景分割的纯卷积模型
https://arxiv.org/2312.06052 近年来,基于Transformer的模型由于其强大的建模能力以及对语义类和实例类的统一表示为全局二值掩码,在全景分割中占据主导地位。 在本文中,我们回顾了纯粹的卷积模型,并提出了一种新的结构MaskConve…...
- 数组)
leetcode初级算法(python)- 数组
文章目录 1.从排序数组中删除重复项2.买卖股票最佳时机23.旋转数组运行颠倒列表法整体移动元素块法4.存在重复运行包含判断法排序比较判断法运行集合判断法5.只出现一次的数字6.两个数组的交集27.移动零8.两数之和9.旋转图像这篇博客中的代码都是数组计算。 1.从排序数组中删除…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
