数据结构-二分搜索树(Binary Search Tree)
一,简单了解二分搜索树
树结构:
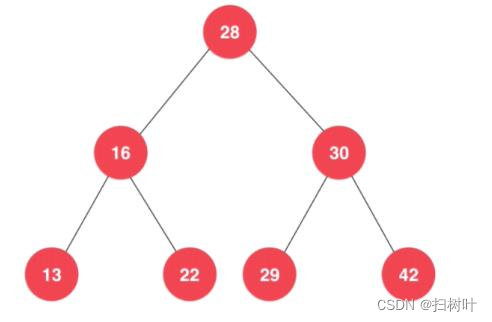
问题:为什么要创造这种数据结构
1,树结构本身是一种天然的组织结构,就好像我们的文件夹一样,一层一层的.

2,树结构可以更高效的处理问题
二,二分搜索树的基础
1、二叉树


2,二叉树的重要特性
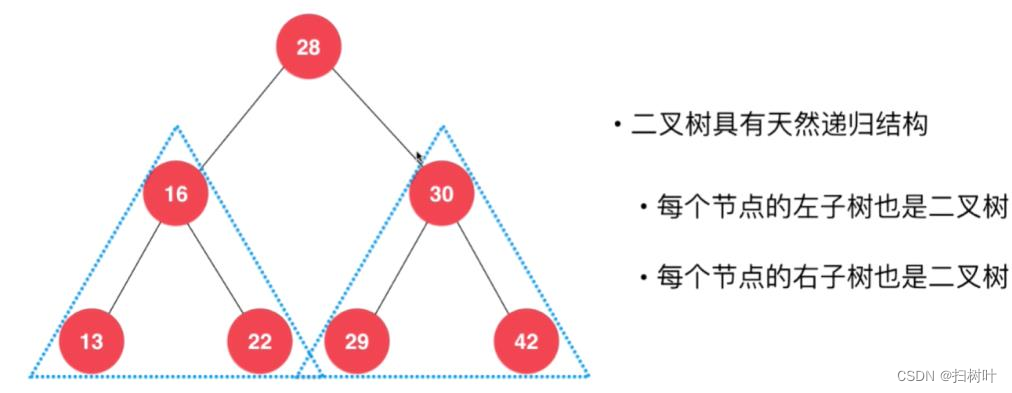 满二叉树
满二叉树

总结:
1. 叶子结点出现在二叉树的最底层,除叶子结点之外的其它结点都有两个孩子结点。
2. 一个层数为k 的满二叉树总结点数为:
3. 第i层上的结点数为:
4. 一个层数为k的满二叉树的叶子结点个数(也就是最后一层):
4、二叉树不一定是“满”的
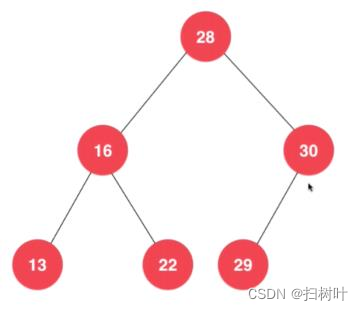
3,二分搜索树


(注意:存储的元素必须具有可比性)
1,向二分搜索树添加元素

2,向二分搜索树查询操作
1,递归终止的条件 : if(node == null ) return false;
2,递归操作
if (ele.compareTo(node.ele) < 0) {
return search(node.left, ele);
} else if (ele.compareTo(node.ele) > 0) {
return search(node.right, ele);
} else {
return true;
}
3,二分搜索树的遍历操作
遍历操作:把树中所有节点都访问一遍
1前序遍历,
2中序遍历,
3后序遍历
4层序遍历(广度优先)
(代码,会在后面一起展现.)
4,二分搜索树寻找最大值,最小值
 同样的原理找出二分搜素树中最大的元素,这里不在过多赘述.
同样的原理找出二分搜素树中最大的元素,这里不在过多赘述.
5,删除操作
情况一:(叶子结点)
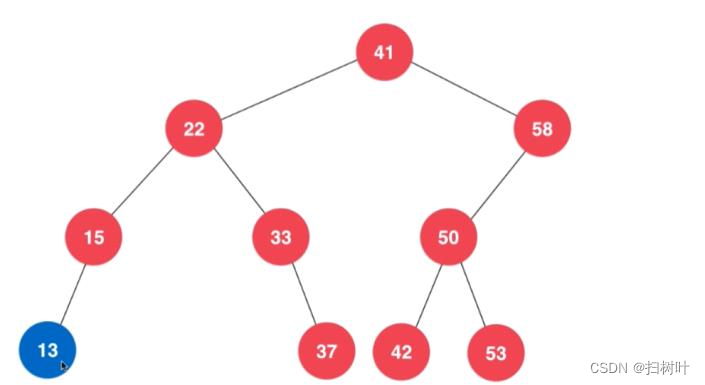
情况二、(非叶子结点)
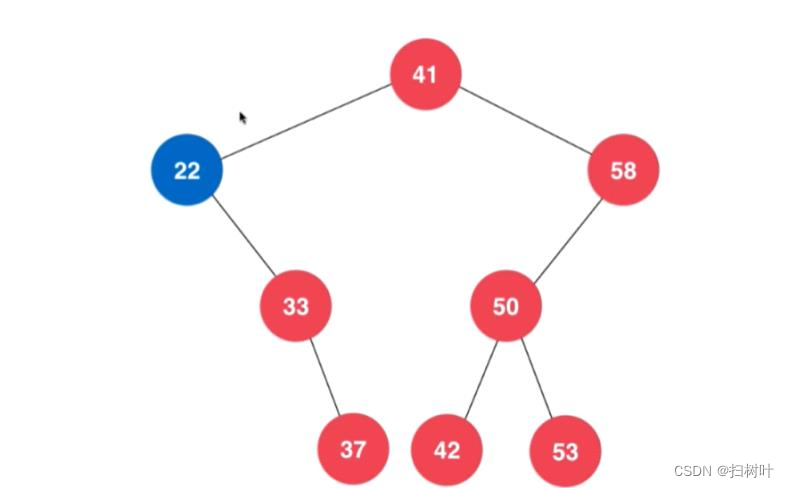
删除后
 6,删除二分搜索树中的节点
6,删除二分搜索树中的节点
情况一:
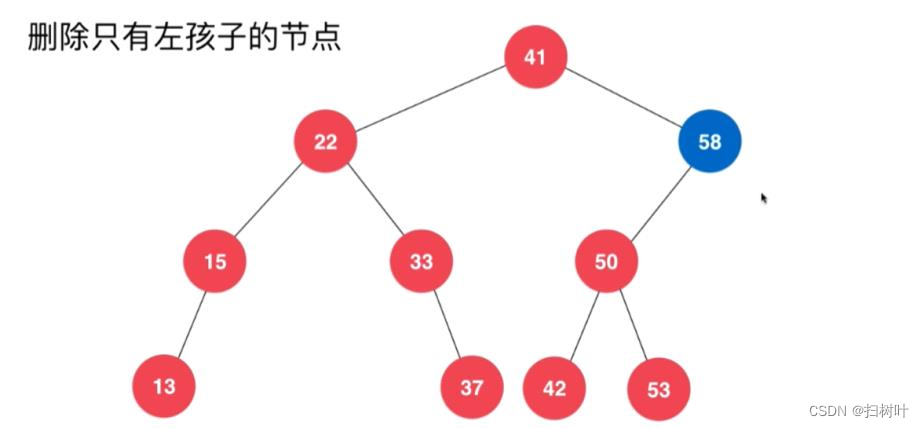
情况二、

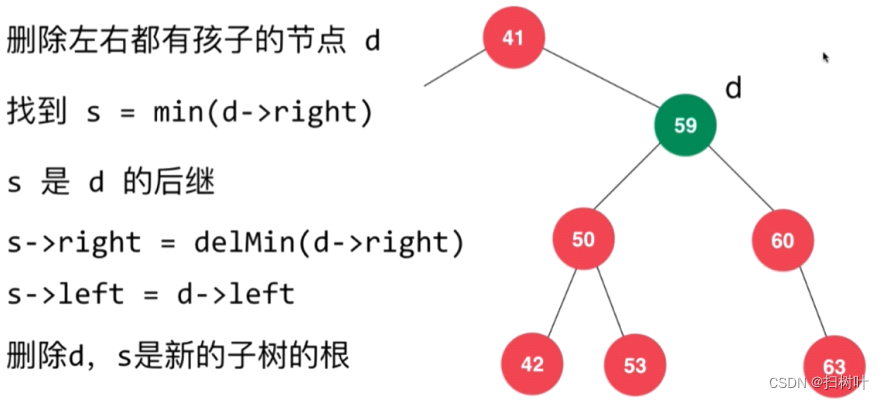
情况三:左右孩子都不为空的情况
使用Hibbard Deletion

三,用代码实现二分搜索树.实现相关功能.
(由于功能实现较多,代码较长)
其中包含是前面的各种功能操作的实现,包括,前,中,后,层,序把遍历,删除,添加,等等操作.需要的同学可以仔细查看.
mport java.nio.channels.Pipe;
import java.util.*;
import java.util.stream.Collectors;// 二分搜索树
public class BinarySearchTree<T extends Comparable<T>> {// 定义树的结点public class Node {T val;Node left; // 左孩子Node right; // 右孩子public Node(T val) {this.val = val;}}// 定义树的根private Node root;// 树根// 统计树中结点的个数private int size;// 树中结点的个数public BinarySearchTree() {this.root = null;this.size = 0;}// 判断树是否为空public boolean isEmpty() {return this.size == 0;}// 获取树中元素的个数public int getSize() {return this.size;}// 向树中添加元素public void add(T val) {this.size++;this.root = add(this.root, val);}/*** 添加的递归方法** @param node 树的根结点* @param val 添加的值*/private Node add(Node node, T val) {//递归终止的条件if (node == null) {Node leafNode = new Node(val);return leafNode;}// 递归操作if (node.val.compareTo(val) > 0) {node.left = add(node.left, val);} else {node.right = add(node.right, val);}return node;}// 将树中所有结点进行遍历--中序遍历( 深度优先搜索 DFS,使用的栈来实现)public String middleTravel() {List<T> result = new ArrayList<>();middleTravel(this.root, result);return result.stream().map(item -> item.toString()).collect(Collectors.joining(","));}/*** 中序遍历** @param node 树的根结点*/private void middleTravel(Node node, List<T> result) {// 递归终止的条件if (node == null) {return;}// 递归操作// 先遍历左子树middleTravel(node.left, result);// 打印当前值result.add(node.val);// 再遍历右子树middleTravel(node.right, result);}public String beforeTravel() {List<T> result = new ArrayList<>();beforeTravel(this.root, result);return result.stream().map(item -> item.toString()).collect(Collectors.joining(","));}/*** 前序遍历** @param node 树的根结点*/private void beforeTravel(Node node, List<T> result) {// 递归终止的条件if (node == null) {return;}// 递归操作// 打印当前值result.add(node.val);// 先遍历左子树beforeTravel(node.left, result);// 再遍历右子树beforeTravel(node.right, result);}public String afterTravel() {List<T> result = new ArrayList<>();afterTravel(this.root, result);return result.stream().map(item -> item.toString()).collect(Collectors.joining(","));}/*** 后序遍历** @param node 树的根结点*/private void afterTravel(Node node, List<T> result) {// 递归终止的条件if (node == null) {return;}// 递归操作// 先遍历左子树afterTravel(node.left, result);// 再遍历右子树afterTravel(node.right, result);// 打印当前值result.add(node.val);}// 查找的方法public boolean contains(T val) {return contains(this.root, val);}/*** 从以node为根的二分搜索树中查找元素val** @param node 根节点* @param val 要搜索的值* @return*/private boolean contains(Node node, T val) {// 递归到底的情况if (node == null) {return false;}// 递归操作if (node.val.compareTo(val) == 0) {return true;} else if (node.val.compareTo(val) > 0) {return contains(node.left, val);} else {return contains(node.right, val);}}// 树的层序遍历(广度优先搜索 BFS,使用队列来实现)public String levelTravel() {List<String> list = new ArrayList<>();// 1、 创建一个队列Queue<AbstractMap.SimpleEntry<Integer, Node>> queue = new LinkedList<>();// 2、将根结点入入队if (this.root != null) {queue.offer(new AbstractMap.SimpleEntry<>(1, this.root));}// 3、遍历队列while (!queue.isEmpty()) {AbstractMap.SimpleEntry<Integer, Node> temp = queue.poll();Node value = temp.getValue();int key = temp.getKey();//3-1 先将内容保存list.add(value.val.toString() + "------" + key);// 3-2 判断左子树是否为空,不为空就入队if (value.left != null) {queue.offer(new AbstractMap.SimpleEntry<>(key + 1, value.left));}// 3-3 判断右子树是否为空,不为空就入队if (value.right != null) {queue.offer(new AbstractMap.SimpleEntry<>(key + 1, value.right));}}return list.stream().collect(Collectors.joining(","));}public List<List<T>> levelOrder() {// 返回值类型是啥,就创建啥List<List<T>> result = new ArrayList<>();// 1、 创建一个队列Queue<AbstractMap.SimpleEntry<Integer, Node>> queue = new LinkedList<>();// 2、将根结点入入队if (this.root != null) {queue.offer(new AbstractMap.SimpleEntry<>(1, this.root));}while (!queue.isEmpty()) {AbstractMap.SimpleEntry<Integer, Node> temp = queue.poll();Node value = temp.getValue();int key = temp.getKey();//3-1 先将内容保存if(result.get(key-1)==null){result.add(new ArrayList<>());}result.get(key-1).add(value.val);// 3-2 判断左子树是否为空,不为空就入队if (value.left != null) {queue.offer(new AbstractMap.SimpleEntry<>(key + 1, value.left));}// 3-3 判断右子树是否为空,不为空就入队if (value.right != null) {queue.offer(new AbstractMap.SimpleEntry<>(key + 1, value.right));}}return result;}// Pair对public class Pair<Node> {private Node value; // 保存值private int key; // 保存层public Pair(Node value, int key) {this.value = value;this.key = key;}public Node getValue() {return value;}public int getKey() {return key;}}// 从二分搜索树中找最小值(在整棵树的最左边)public T getMinVal() {// 判断树是否为空if (this.root == null) {return null;}Node curNode = this.root;while (curNode.left != null) {curNode = curNode.left;}return curNode.val;}public T getMinValDG() {// 判断树是否为空if (this.root == null) {return null;}return getMinValDG(this.root).val;}/*** 从以node为根的二分搜索树中查找最小值** @param node 树的根节点*/private Node getMinValDG(Node node) {//递归终止的条件if (node.left == null) {return node;}// 递归操作return getMinValDG(node.left);}// 从二分搜索树中找最 大值(在整棵树的最右边)public T getMaxVal() {// 判断树是否为空if (this.root == null) {return null;}Node curNode = this.root;while (curNode.right != null) {curNode = curNode.right;}return curNode.val;}public T getMaxValDG() {// 判断树是否为空if (this.root == null) {return null;}return getMaxValDG(this.root).val;}private Node getMaxValDG(Node node) {//递归终止的条件if (node.right == null) {return node;}// 递归操作return getMinValDG(node.right);}// 从以this.root为根的二分搜索树中删除最小的结点public void removeMinNode() {if (this.root == null) {return;}this.root = removeMinNode(this.root);}/*** 从以node为根的二分搜索树中删除最小的节点** @param node 树的根节点* @return 删除之后的树的根节点*/private Node removeMinNode(Node node) {// 递归终止的条件if (node.left == null) {this.size--;return node.right;}// 递归操作node.left = removeMinNode(node.left);return node;}// 删除操作public void remove(T val) {if (!contains(val)) {return;}this.root = remove(this.root, val);}/*** 从以node为根的二分搜索树中删除元素val的节点** @param node 树的根节点* @param val 删除的值* @return*/private Node remove(Node node, T val) {// 递归终止的条件if (node == null) {return null;}if (node.val.compareTo(val) == 0) {// 更新sizethis.size--;if (node.right == null) {//1、右子树为空return node.left;} else if (node.left == null) {//2、左子树为空return node.right;} else {// 3、左右子树都不为空// 3-1 找到删除节点的后继Node suffixNode = getMinValDG(node.right);// 3-2 更新suffixNode的左右子树
// suffixNode.right = removeMinNode(node.right);suffixNode.right = remove(node.right, getMinValDG(node.right).val);suffixNode.left = node.left;this.size++;// 3-3 返回suffixNodereturn suffixNode;}}// 递归操作if (node.val.compareTo(val) > 0) {node.left = remove(node.left, val);} else {node.right = remove(node.right, val);}return node;}}
相关文章:
数据结构-二分搜索树(Binary Search Tree)
一,简单了解二分搜索树 树结构: 问题:为什么要创造这种数据结构 1,树结构本身是一种天然的组织结构,就好像我们的文件夹一样,一层一层的. 2,树结构可以更高效的处理问题 二,二分搜索树的基础 1、二叉树 2,二叉树的重要特性 满二叉树 总结: 1. 叶子结点出现在二叉树的最…...

YOLO如何训练自己的模型
目录 步骤 一、打标签 二、数据集 三、跑train代码出模型 四、跑detect代码出结果 五、详细操作 步骤 一、打标签 (1)在终端 pip install labelimg (2)在终端输入labelimg打开 如何打标签: 推荐文章…...
05 EXTI外部中断
一、中断系统 中断系统:管理和执行中断的逻辑结构。中断:在主程序运行过程中,出现了特定的中断触发条件——中断源,使得CPU暂停当前正在运行的程序,转而去处理中断程序,处理完成后又返回原来被暂停的位置继…...

2024.2.23
1.1.1 信号默认、捕获、忽略处理(普通信号) #include <myhead.h> void handler(int signo) {if(signoSIGINT){printf("用户键入 ctrlc\n");} } int main(int argc, const char *argv[]) {//忽略信号if(signal(SIGINT,SIG_IGN)SIG_ERR){perror("signal er…...

PHP实现分离金额和其他内容便于统计计算
得到的结果可以粘贴到excel计算 <?php if($_GET["x"] "cha"){ $tips isset($_POST[tips]) ? $_POST[tips] : ; $pattern /(\d\.\d|\d)/; $result preg_replace($pattern, "\t\${1}\t", $tips); echo "<h2><strong>数…...

基础数据结构和算法《》
递归 1.递归应该一种比较常见的实现一些特殊代码逻辑时需要做的,但常常也是最绕的一种方式,在解释递归 之前,我们用循环和递归来做个比较1.1.如果你打开一扇门后,同样发现前方也有一扇们,紧接着你又打开下一扇门...直…...
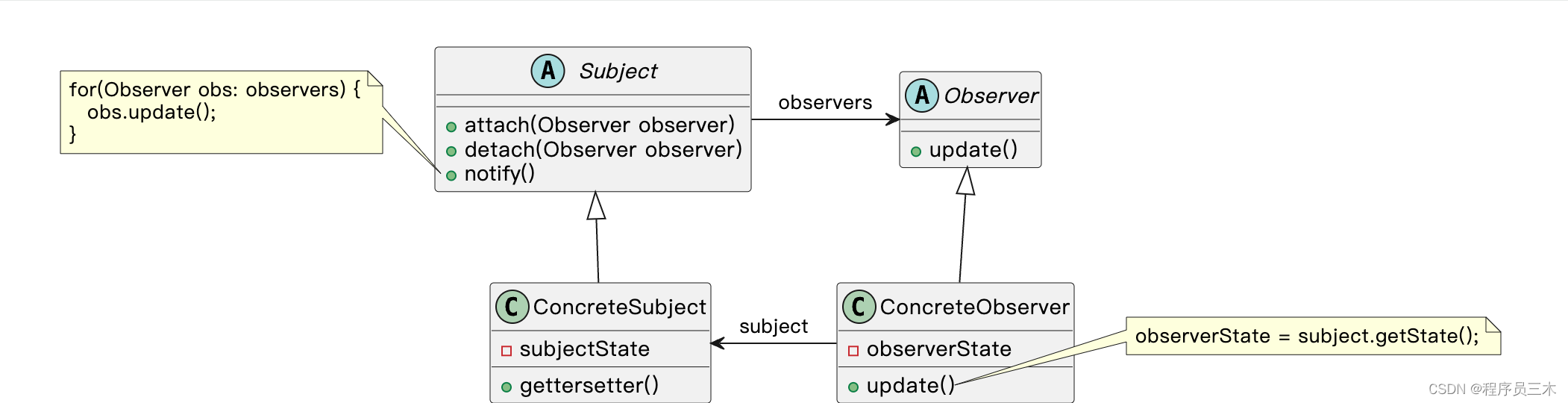
[设计模式Java实现附plantuml源码~行为型]对象间的联动~观察者模式
前言: 为什么之前写过Golang 版的设计模式,还在重新写Java 版? 答:因为对于我而言,当然也希望对正在学习的大伙有帮助。Java作为一门纯面向对象的语言,更适合用于学习设计模式。 为什么类图要附上uml 因为很…...
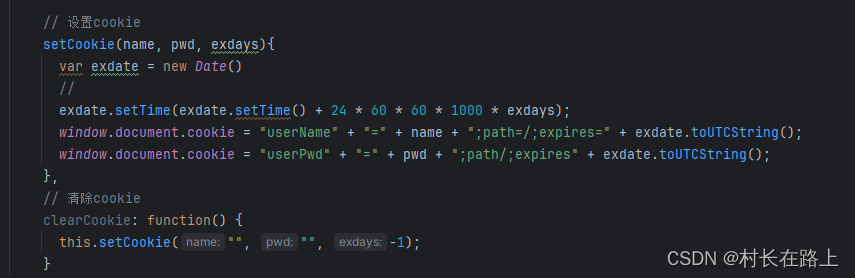
vue3+js 实现记住密码功能
常见的几种实现方式 1 基于spring security 的remember me 功能 localStorage 除非主动清除localStorage 里的信息 ,不然永远存在,关闭浏览器之后下次启动仍然存在 存放数据大小一般为5M 不与服务器进行交互通信 cookies 可以…...

基于单片机的太阳能电池板自动跟踪系统的研究
摘要 伴随着人类社会的发展,人口基数越来越大,电量消耗巨大,传统发电原 料污染环境的同时,可用量日益减少,给人类未来生产生活带来了一定的威胁, 因而解决日益剧增的用电量,寻求一种新能源显得极其重要。论文正是基于此 背景下,针对当前太阳能电池板采光率低、自动化水…...

React 模态框的设计(二)
自定义组件是每个前端开发者必备的技能。我们在使用现有框架时难免有一些超乎框架以处的特别的需求,比如关于弹窗,每个应用都会用到,但是有时我们使用的框架中提供的弹窗功能也是功能有限,无法满足我们的应用需求,今天…...

操作符详解3
✨✨ 欢迎大家来到莉莉的博文✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 前面我们已经讲过算术操作符、赋值操作符、逻辑操作符、条件操作符和部分的单目操作 符,今天继续介绍一部分。 目录 1.操作符的分类 2…...

【C语言基础】:操作符详解(一)
文章目录 操作符详解1. 操作符的分类2. 二进制和进制转换2.1 什么是二进制、八进制、十进制、十六进制2.1.1 二进制和进制转换2.1.2 二进制转十进制2.2.3 二进制转八进制2.2.4 二进制转十六进制 3. 源码、反码、补码4. 移位操作符4.1 左移操作符4.2 右移操作符 5. 位操作符&…...
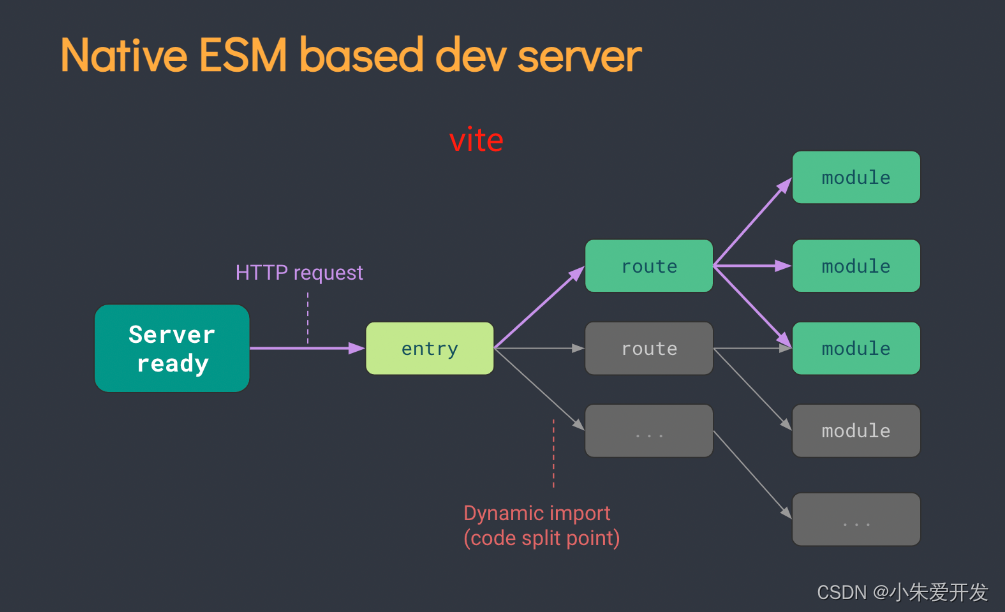
通俗易懂分析:Vite和Webpack的区别
1、对项目构建的理解 先从浏览器出发, 浏览器是由浏览器内核和JS引擎组成;浏览器内核编译解析html代码和css代码,js引擎编译解析JavaScript代码;所以从本质上,浏览器只能识别运行JavaScript、CSS、HTML代码。 而我们在…...

OpenCart程序结构与业务逻辑
一、程序业务逻辑说明 在 OpenCart 中,index.php 文件是整个应用程序的入口文件,它负责初始化应用程序并调度请求。以下是 index.php 文件加载执行的流程: 1. **设置路径常量:** - index.php 首先定义了一些重要的路径常量&…...
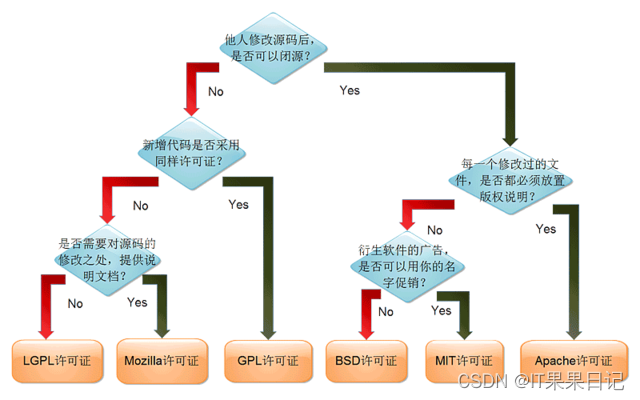
软件License授权原理
软件License授权原理 你知道License是如何防止别人破解的吗?本文将介绍License的生成原理,理解了License的授权原理你不但可以防止别人破解你的License,你甚至可以研究别人的License找到它们的漏洞。喜欢本文的朋友建议收藏+关注,方便以后复习查阅。 什么是License? 在…...

C/C++实现老鼠走迷宫
老鼠形象可以辨认,可以用上下左右操纵老鼠;正确检测结果,若老鼠在规定的时间内走到粮仓,提示成功,否则提示失败。代码分为3个文件:main.cpp、play.h、play.cpp。 main.cpp: #include <iostream> #include <…...

[Linux]文件基础-如何管理文件
回顾C语言之 - 文件如何被写入 fopen fwrite fread fclose fseek … 这一系列函数都是C语言中对文件进行的操作: int main() {FILE* fpfopen("text","w");char str[20]"write into text";fputs(str,fp);fclose(fp);return 0; }而上…...
bat 查找文件所在
脚本 在批处理文件(.bat)中查找文件所在的目录,你可以使用dir命令结合循环和条件语句来实现。以下是一个简单的示例,演示如何在批处理文件中查找指定文件并输出其所在目录: echo off setlocal enabledelayedexpansio…...

程序员的守护神:为何电脑永不熄灭?
在这个信息时代,程序员成了推动社会进步的“隐形英雄”。他们通宵达旦,手指在键盘上跳跃,创造出一个个令人惊叹的数字世界。有趣的是,你可能注意到了一个现象:程序员似乎总是不关电脑。这并非他们对电脑上瘾࿰…...
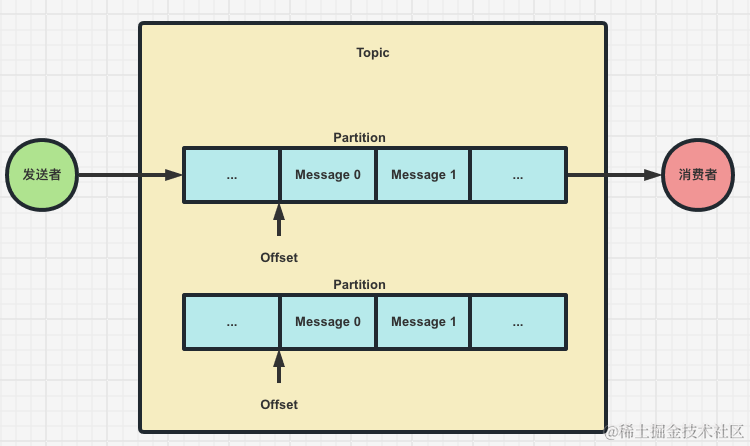
Kafka快速实战以及基本原理详解
Kafka快速实战以及基本原理详解 基本概念 Kafka是一个分布式、支持分区、多副本,基于ZK的分布式消息系统,最大的特性就是可以实时的处理大量数据以满足各种需求场景,比如Hadoop的批处理系统、低延迟的实时系统、Storm/Spark流式处理引擎、日…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

