二叉树与堆
目录
1.树概念及结构
1.1树的概念
1.2 树的相关概念
1.3 树的表示
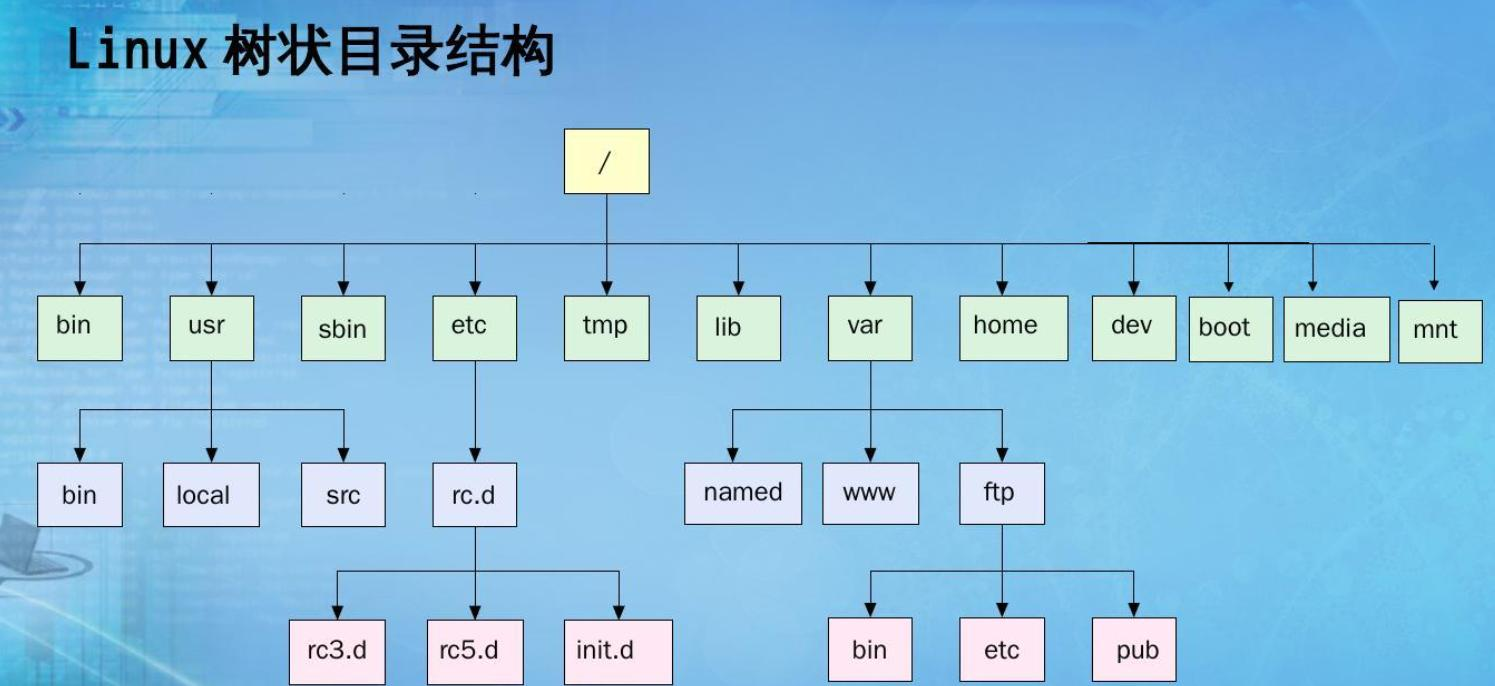
1.4 树在实际中的运用(表示文件系统的目录树结构)
2.二叉树概念及结构
2.1概念
2.2现实中的二叉树:
2.3 特殊的二叉树:
2.4 二叉树的性质
2.5 二叉树的存储结构
3.二叉树的顺序结构及实现
3.1 二叉树的顺序结构
3.2 堆的概念及结构
3.3 堆的实现
3.2.1 堆向下调整算法
3.2.2堆的创建
3.2.3 建堆时间复杂度
3.2.4 堆的插入
3.2.5 堆的删除
3.2.6 堆的代码实现
3.4 堆的应用
3.4.1 堆排序
3.4.2 TOP-K问题
4.二叉树链式结构的实现
4.1 前置说明
4.2二叉树的遍历
4.2.1 前序、中序以及后序遍历
4.2.2 层序遍历
4.3 节点个数以及高度等
4.5 二叉树的创建和销毁
1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
因此,树是递归定义的。

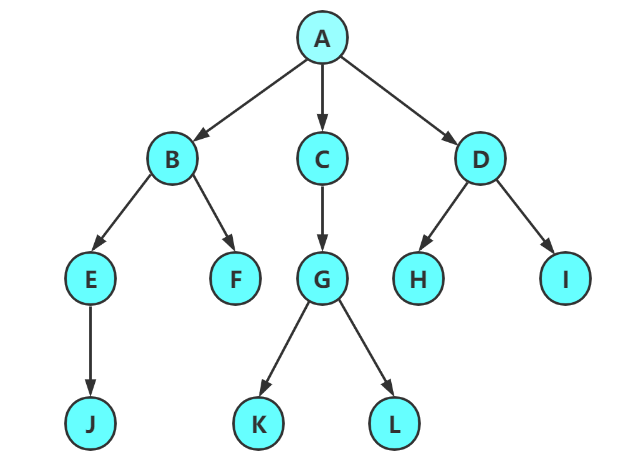
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
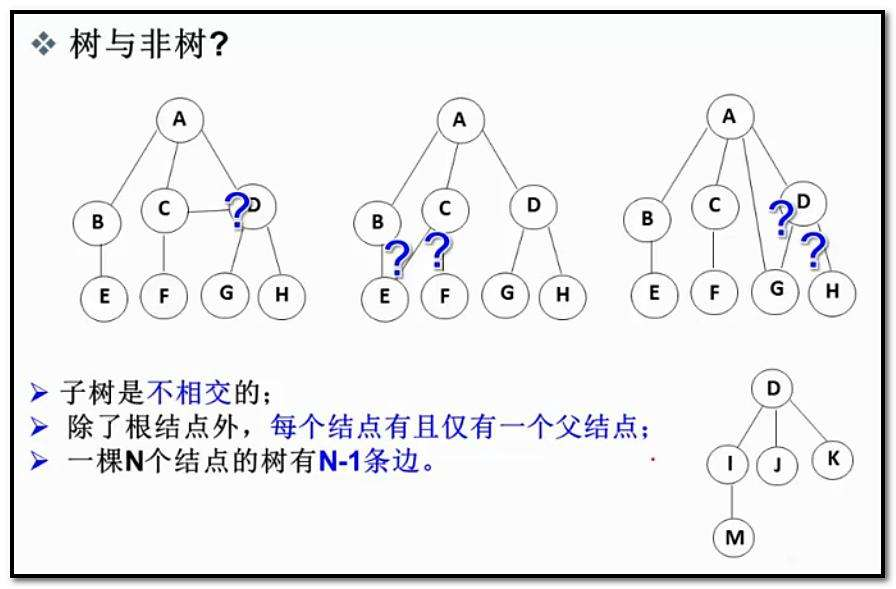
1.2 树的相关概念
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
1.3 树的表示
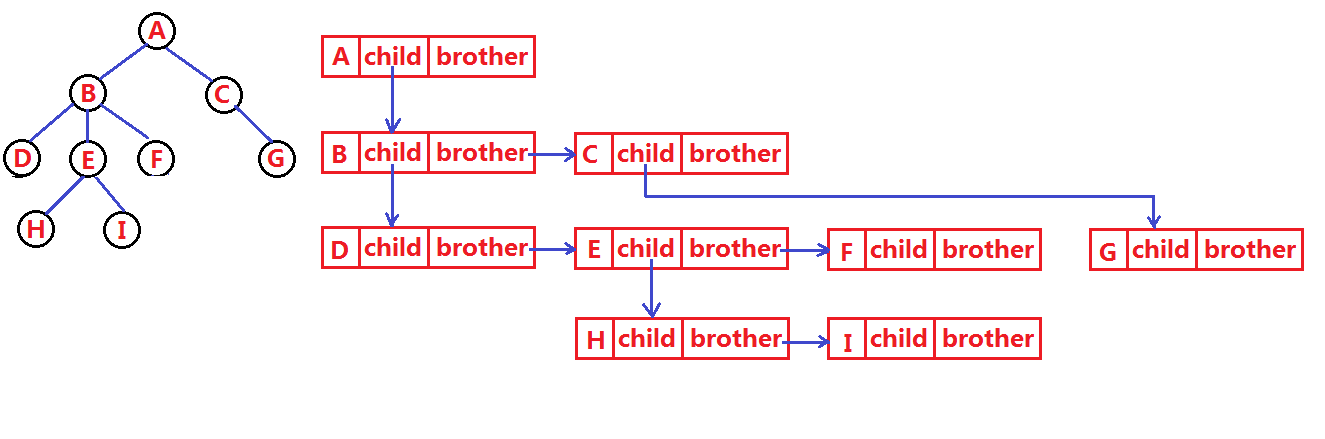
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{
struct Node* _firstChild1; // 第一个孩子结点
struct Node* _pNextBrother; // 指向其下一个兄弟结点
DataType _data; // 结点中的数据域
};
1.4 树在实际中的运用(表示文件系统的目录树结构)
2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
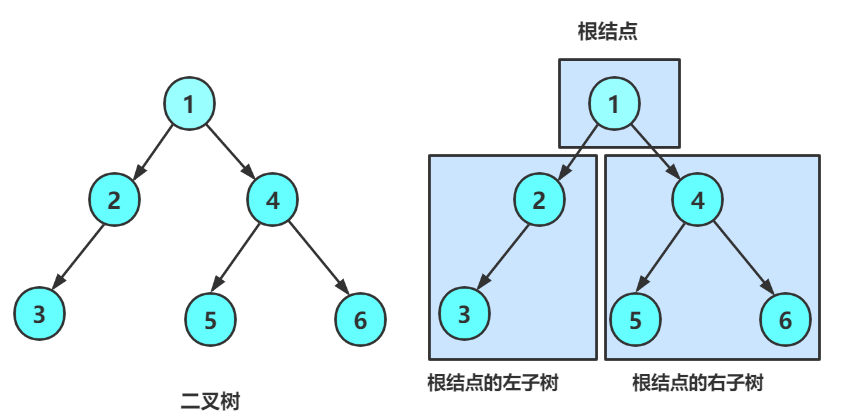
从上图可以看出:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
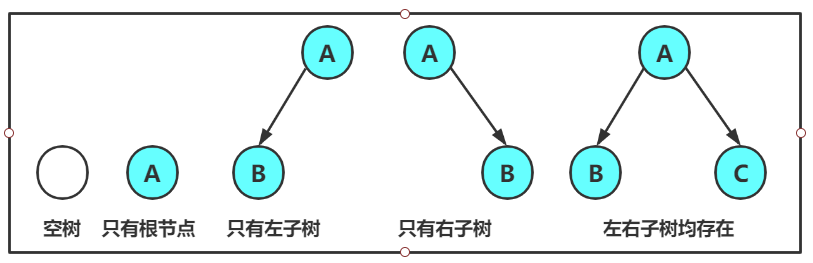
注意:对于任意的二叉树都是由以下几种情况复合而成的:
2.2现实中的二叉树:
2.3 特殊的二叉树:
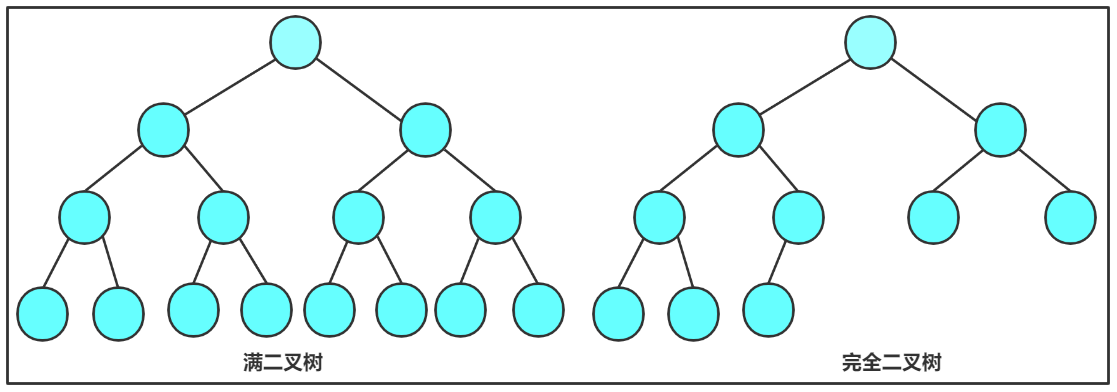
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉 树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树
2.4 二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 .
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 , 度为2的分支结点个数为 ,则有 = +1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= . (ps: 是log以2
为底,n+1为对数)
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
2.5 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
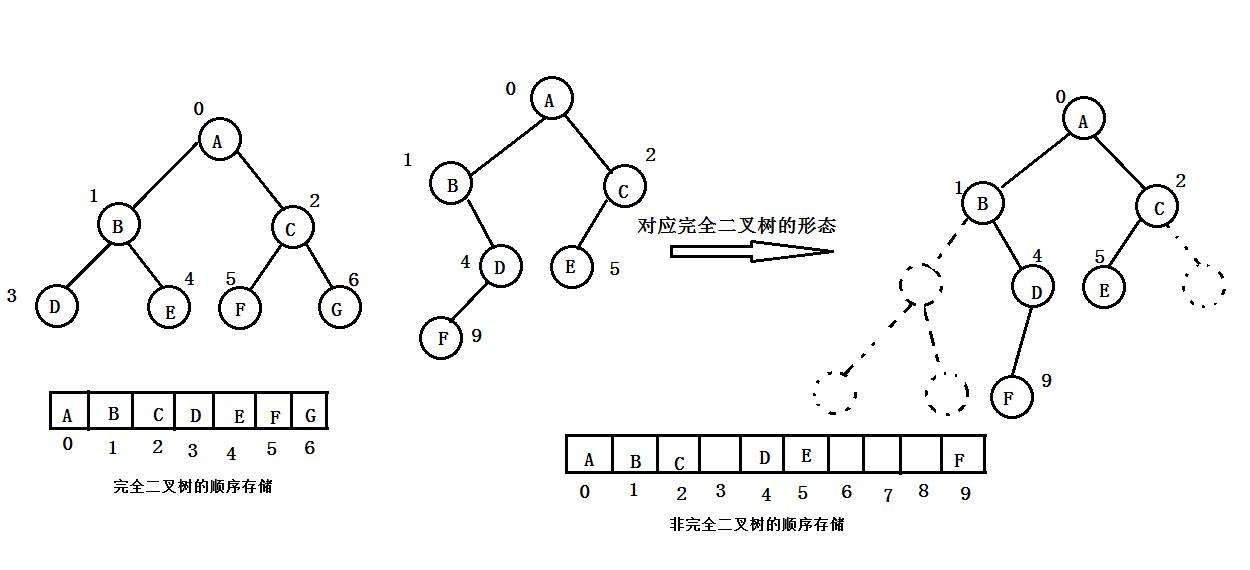
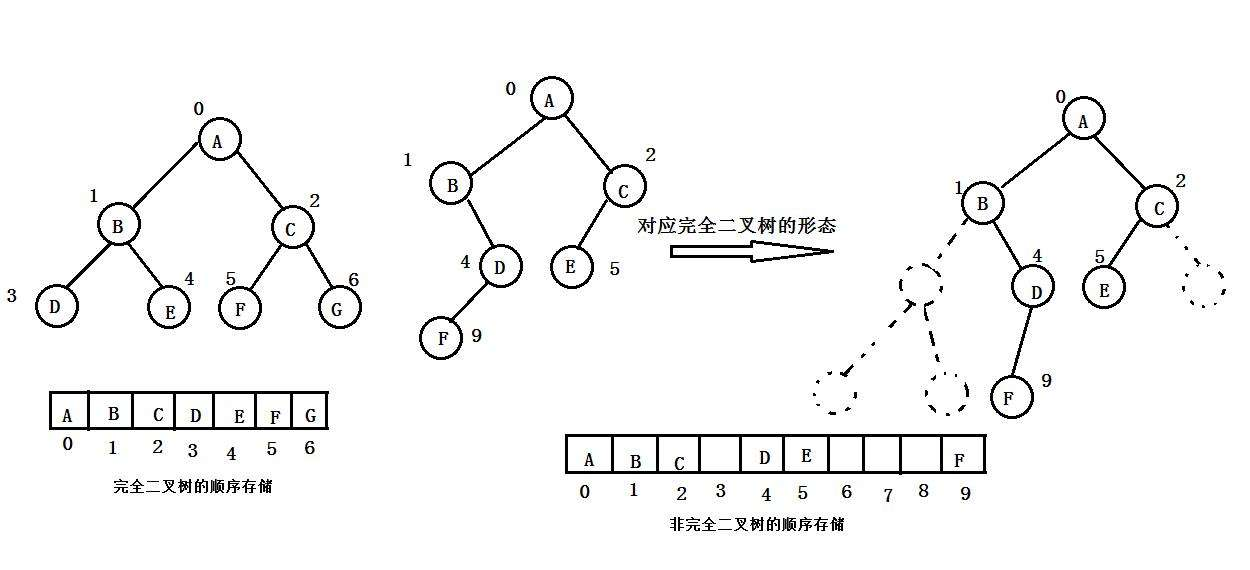
1. 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
2. 链式存储
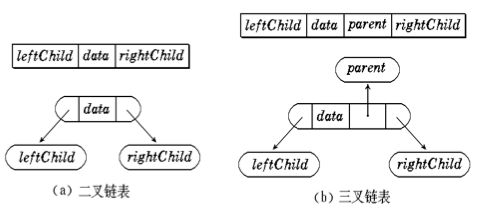
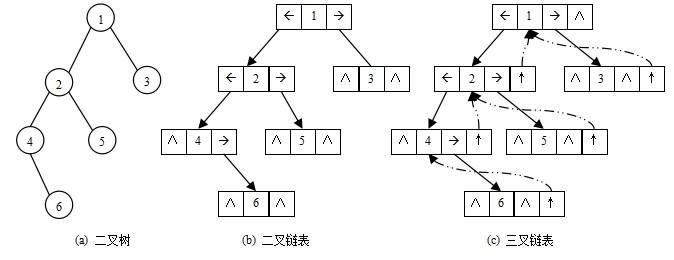
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,如红黑树等会用到三叉链。
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{
struct BinTreeNode* _pParent; // 指向当前节点的双亲
struct BinTreeNode* _pLeft; // 指向当前节点左孩子
struct BinTreeNode* _pRight; // 指向当前节点右孩子
BTDataType _data; // 当前节点值域
};
3.二叉树的顺序结构及实现
3.1 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
3.2 堆的概念及结构

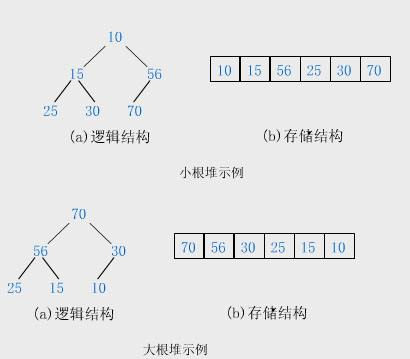
3.3 堆的实现
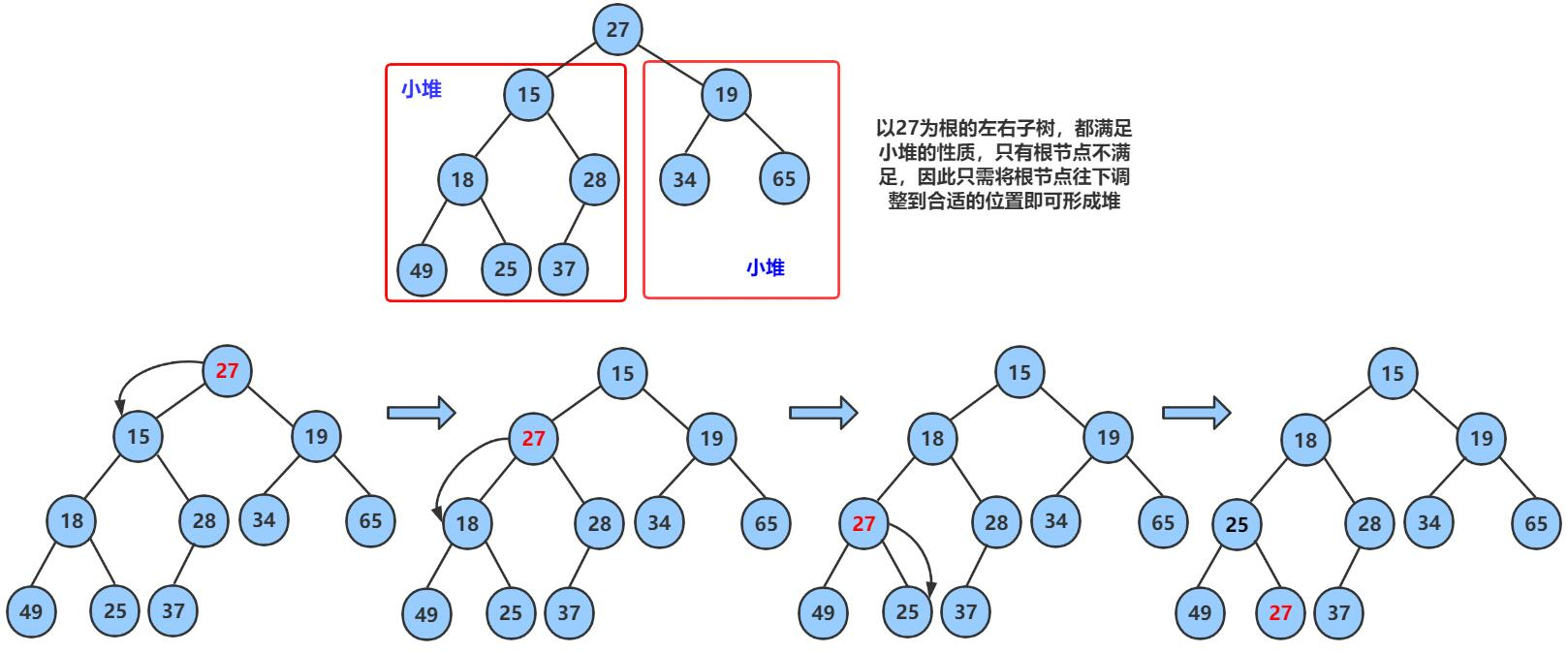
3.2.1 堆向下调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int array[] = {27,15,19,18,28,34,65,49,25,37};
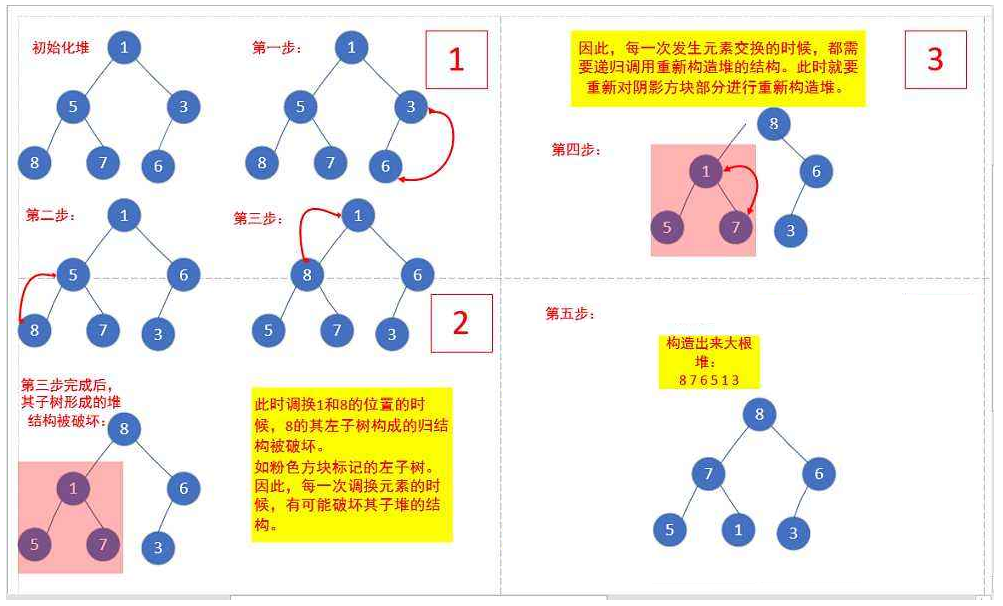
3.2.2堆的创建
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?这里我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
int a[] = {1,5,3,8,7,6};
3.2.3 建堆时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):
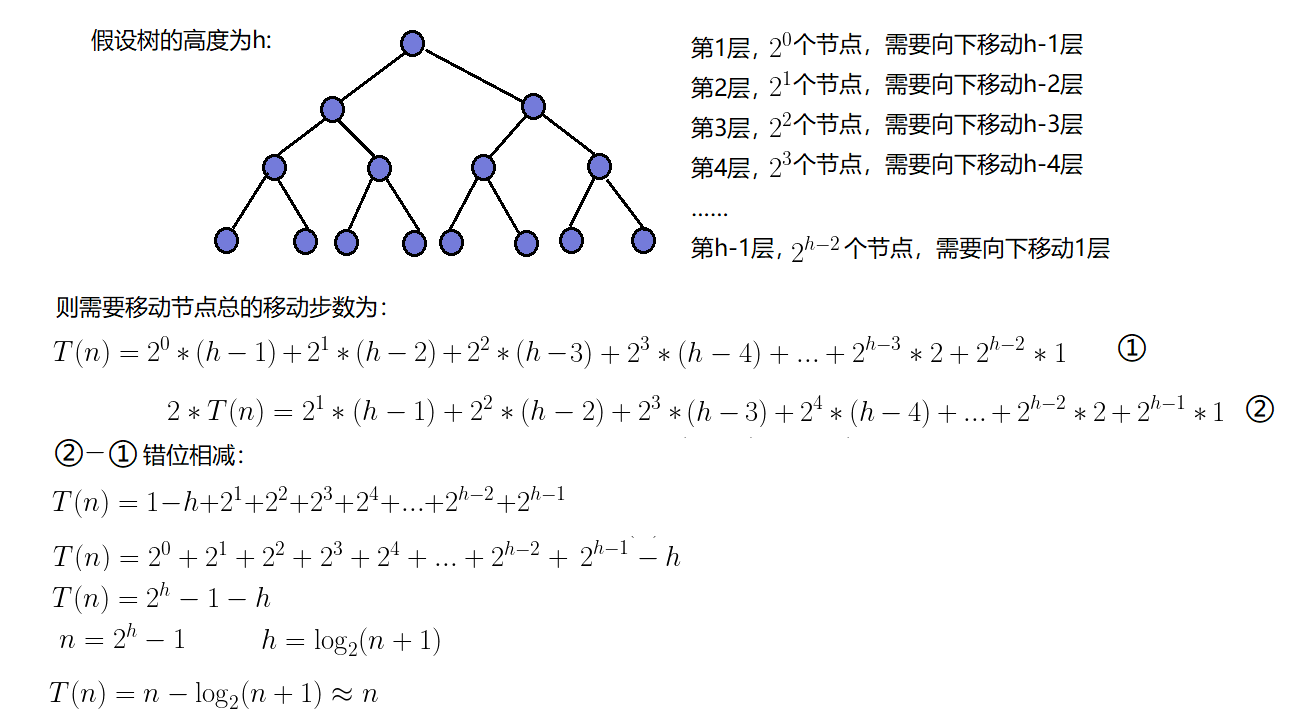
因此:建堆的时间复杂度为O(N)。
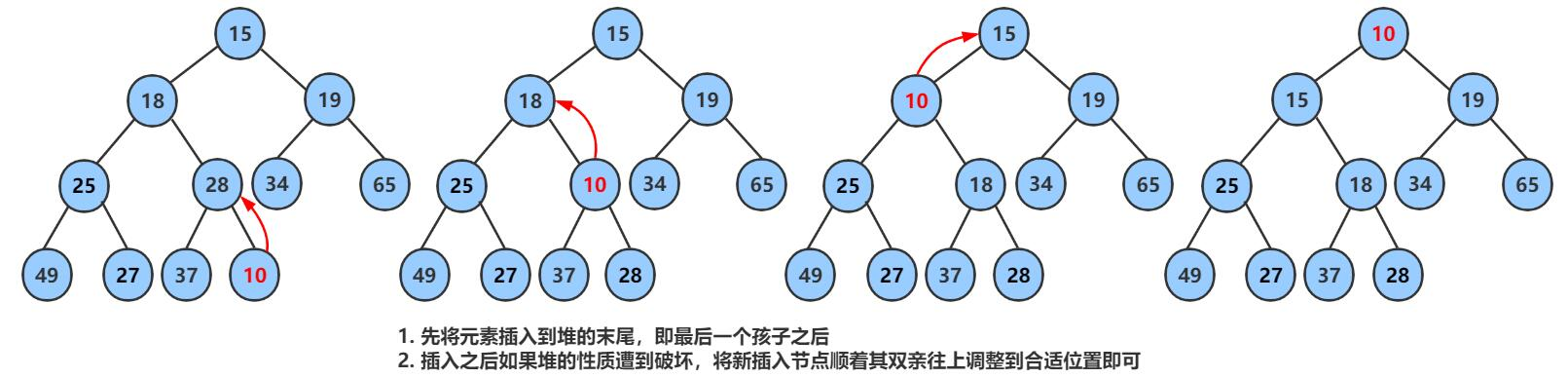
3.2.4 堆的插入
先插入一个10到数组的尾上,再进行向上调整算法,直到满足堆。
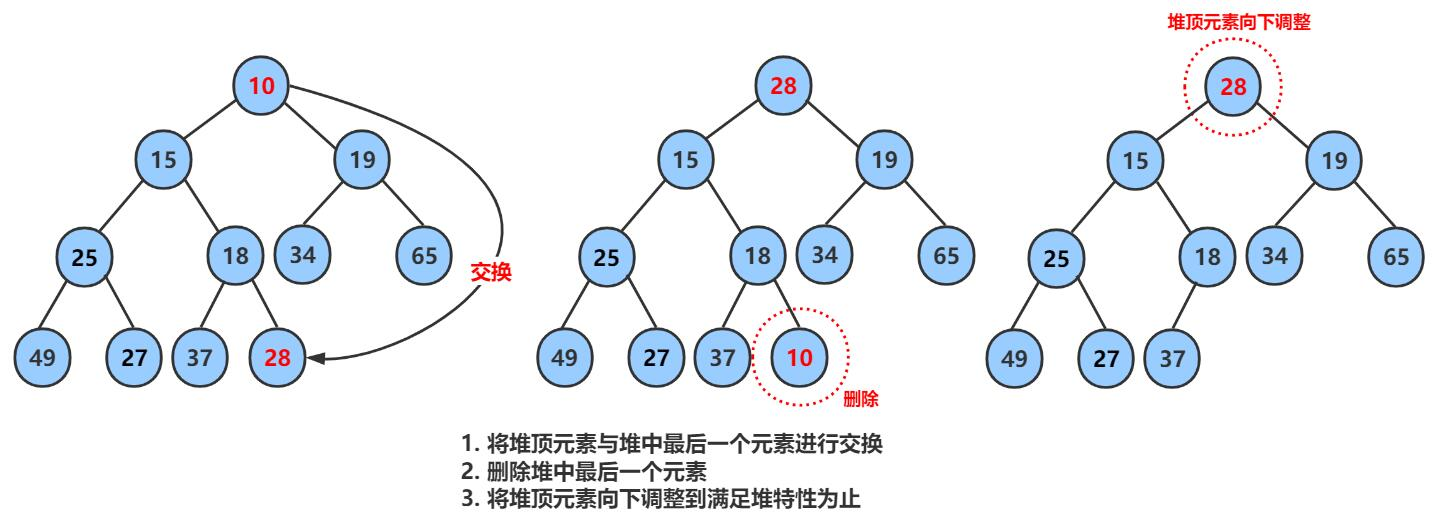
3.2.5 堆的删除
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。
3.2.6 堆的代码实现
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
3.4 堆的应用
3.4.1 堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
1. 建堆
升序:建大堆
降序:建小堆
2. 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序
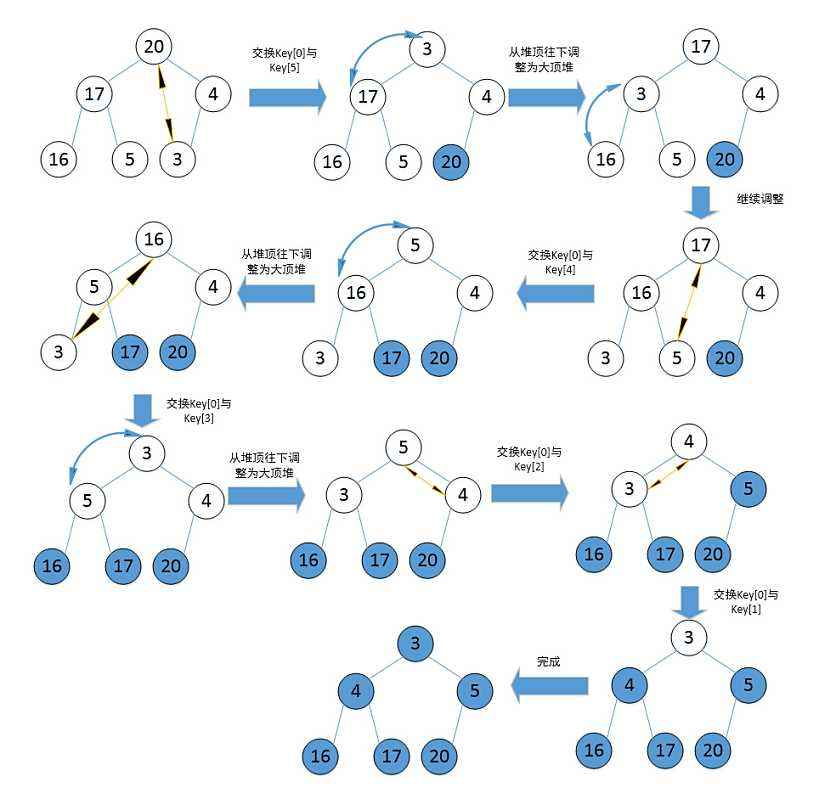
3.4.2 TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排 序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
void PrintTopK(int* a, int n, int k)
{
// 1. 建堆--用a中前k个元素建堆
// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
}
void TestTopk()
{
int n = 10000;
int* a = (int*)malloc(sizeof(int)*n);
srand(time(0));
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2335] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 9;
a[3144] = 1000000 + 10;
PrintTopK(a, n, 10);
}
4.二叉树链式结构的实现
4.1 前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->_left = node2;
node1->_right = node4;
node2->_left = node3;
node4->_left = node5;
node4->_right = node6;
return node1;
}
注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解。
再看二叉树基本操作前,再回顾下二叉树的概念,二叉树是:
1. 空树
2. 非空:根节点,根节点的左子树、根节点的右子树组成的
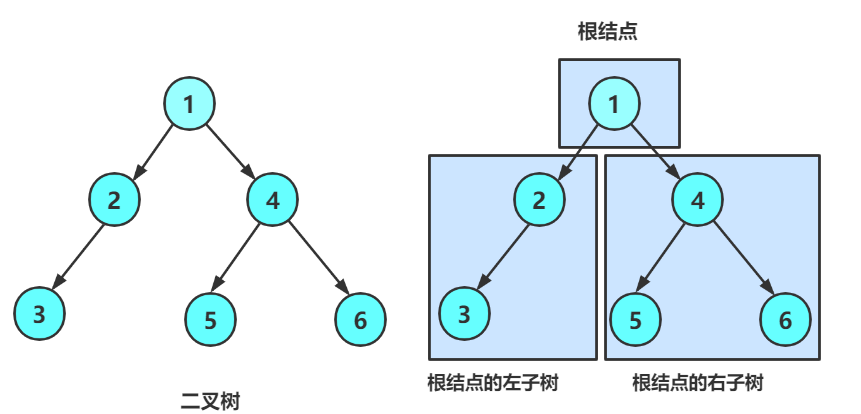
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
4.2二叉树的遍历
4.2.1 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。

按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);
下面主要分析前序递归遍历,中序与后序图解类似,同学们可自己动手绘制。
前序遍历递归图解:
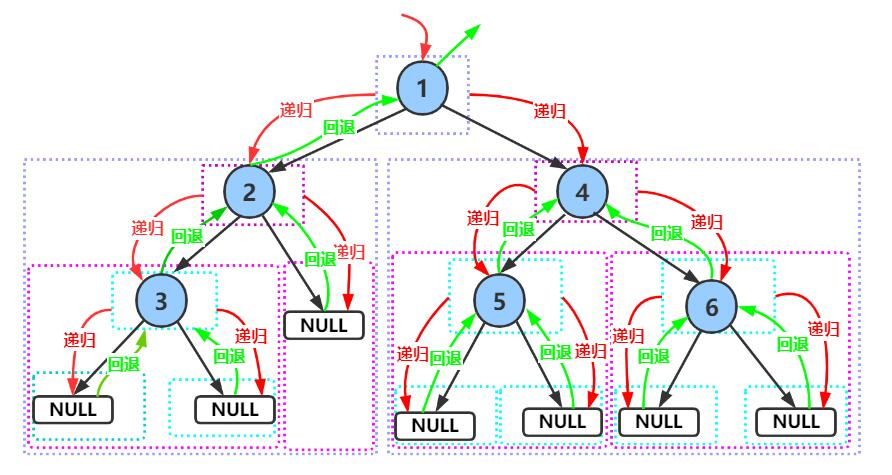
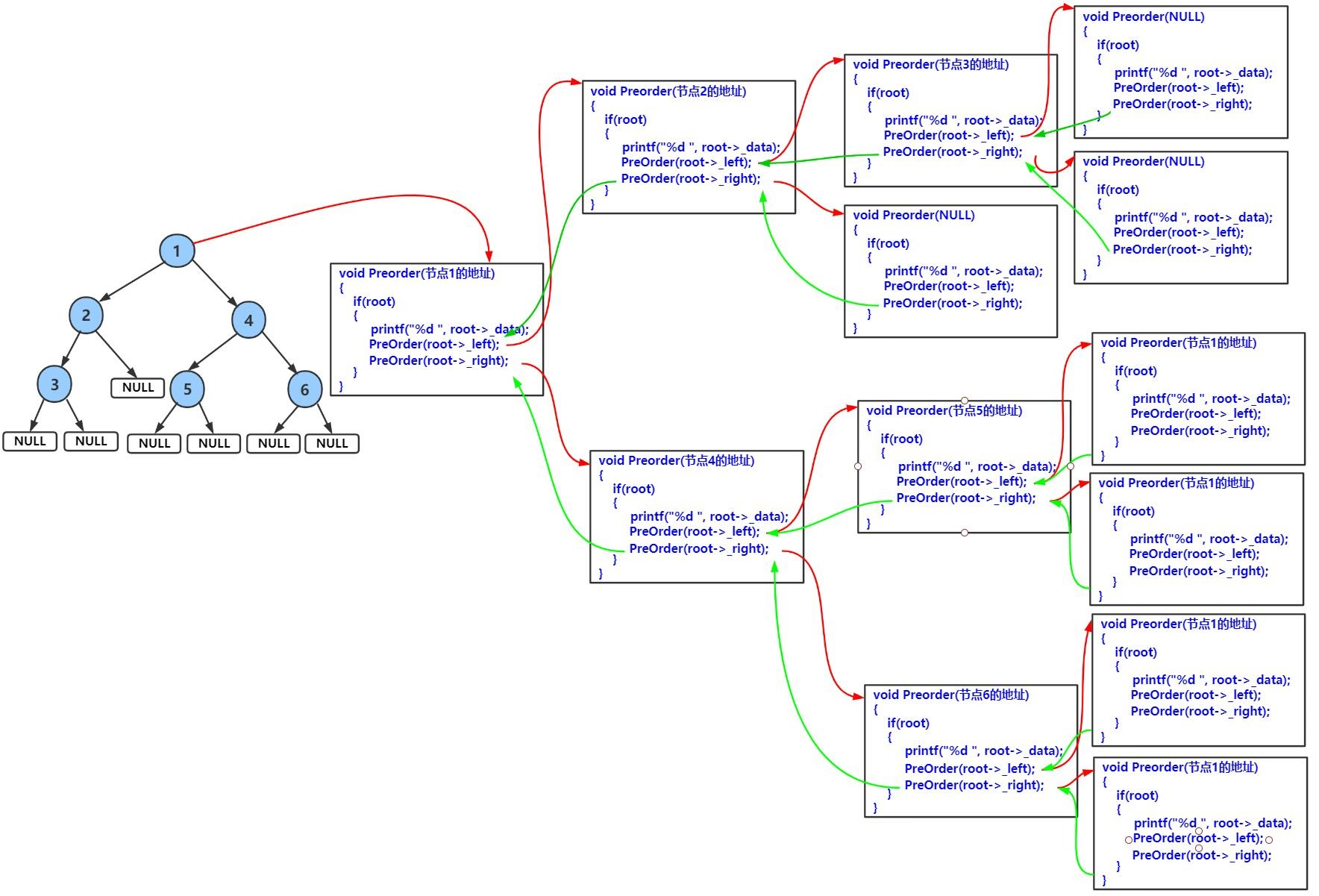
前序遍历结果:1 2 3 4 5 6
中序遍历结果:3 2 1 5 4 6
后序遍历结果:3 2 5 6 4 1
4.2.2 层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
// 层序遍历
void LevelOrder(BTNode* root);
4.3 节点个数以及高度等
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
4.5 二叉树的创建和销毁
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);
相关文章:

二叉树与堆
目录 1.树概念及结构 1.1树的概念 1.2 树的相关概念 1.3 树的表示 1.4 树在实际中的运用(表示文件系统的目录树结构) 2.二叉树概念及结构 2.1概念 2.2现实中的二叉树: 2.3 特殊的二叉树: 2.4 二叉树的性质 2.5 二叉树的…...

神经网络系列---损失函数
文章目录 损失函数均方误差(Mean Squared Error,MSE):平均绝对误差(Mean Absolute Error,MAE):交叉熵损失函数(Cross-Entropy Loss):Hinge Loss&a…...
)
LeetCode每日一题 有效的字母异位词(哈希表)
题目描述 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。 示例 1: 输入: s "anagram", t "nagaram" 输…...
设计模式学习笔记 - 面向对象 - 8.实践:贫血模型和充血模型的原理及实践
1.Web开发常用的贫血MVC架构违背OOP吗? 前面我们依据讲过了面向对象四大特性、接口和抽象类、面向对象和面向过程编程风格,基于接口而非实现编程和多用组合少用继承设计思想。接下来,通过实战来学习如何将这些理论应用到实际的开发中。 大部…...

AI新纪元:可能的盈利之道
本文来源于Twitter大神宝玉(dotey)在聊 Sora 的时候,总结了 Sora 的价值和可能的盈利方向,我把这部分内容单独摘出来再整理一下。现在的生成式 AI 大家应该不陌生,用它总结文章、翻译、写作、画图,当然真正…...
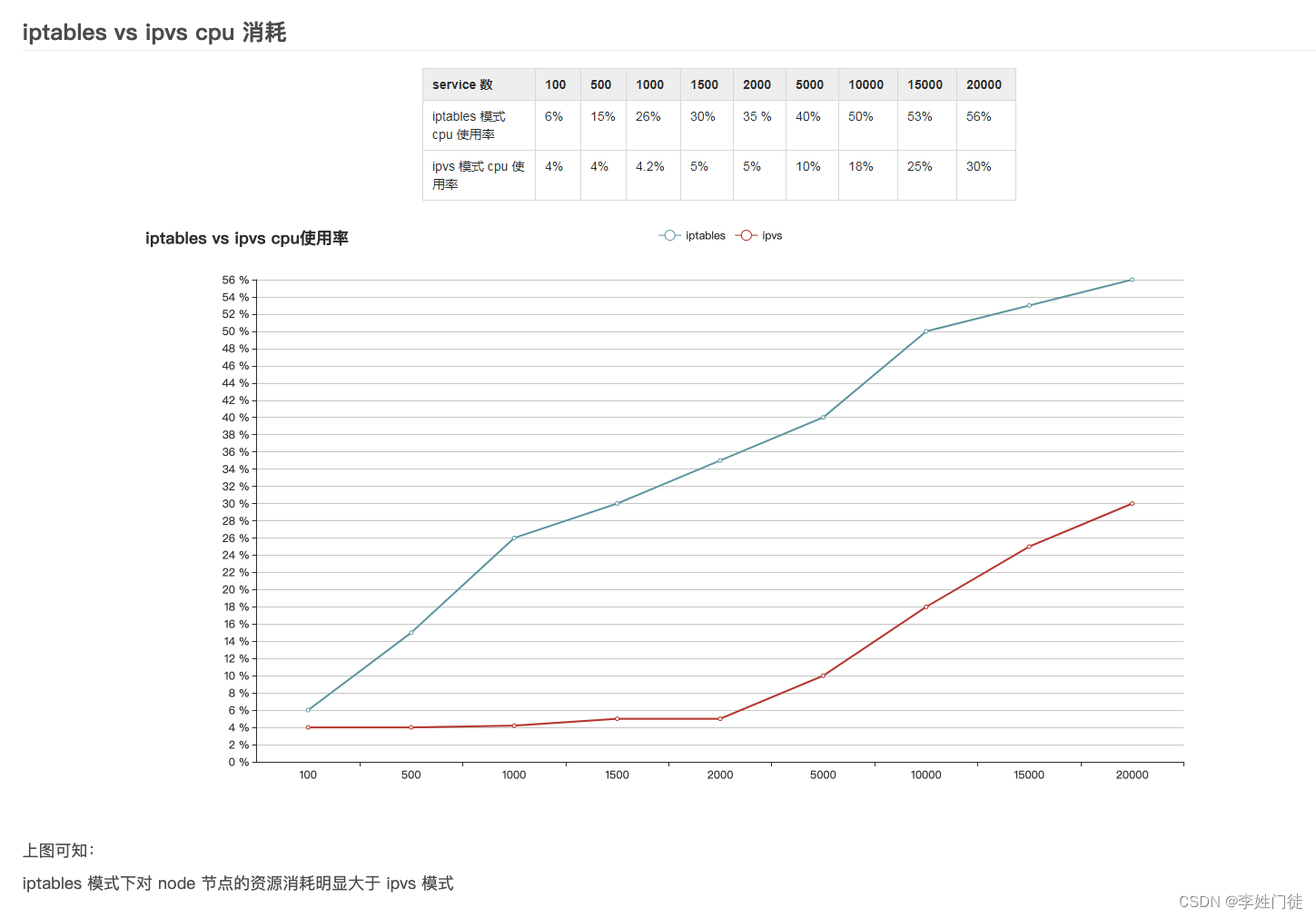
k8s的svc流量通过iptables和ipvs转发到pod的流程解析
文章目录 1. k8s的svc流量转发1.1 service 说明1.2 endpoints说明1.3 pod 说明1.4 svc流量转发的主要工作 2. iptables规则解析2.1 svc涉及的iptables链流程说明2.2 svc涉及的iptables规则实例2.2.1 KUBE-SERVICES规则链2.2.2 KUBE-SVC-EFPSQH5654KMWHJ5规则链2.2.3 KUBE-SEP-L…...
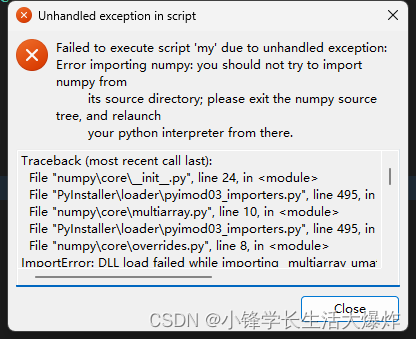
【踩坑】修复报错 you should not try to import numpy from its source directory
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 报错如下: 修复方法一: pip install pyinstaller5.9 修复方法二: pip install numpy1.24.1...

预测脱碳企业的信用评级-论文代码复现
文献来源 【Forecasting credit ratings of decarbonized firms: Comparative assessmentof machine learning models】 文章有代码复现有两个基本工作,1.是提取每个算法的重要性;2.计算每个算法的评价指标 算法有 CRT 分类决策树 ANN 人工神经网络 R…...

目标检测——KITTI目标跟踪数据集
KITTI目标跟踪数据集是由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合创建的一个大规模自动驾驶场景下的计算机视觉算法评测数据集。这个数据集主要用于评估立体图像、光流、视觉测距、3D物体检测和3D跟踪等计算机视觉技术在车载环境下的性能这个数据集包含了在市区、乡村和…...

25-k8s集群中-RBAC用户角色资源权限
一、RBAC概述 1,k8s集群的交互逻辑(简单了解) 我们通过k8s各组件架构,知道各个组件之间是使用https进行数据加密及交互的,那么同理,我们作为“使用”k8s的各种资源的使用者,也是通过https进行数…...
Android 面试问题 2024 版(其二)
Android 面试问题 2024 版(其二) 六、多线程和并发七、性能优化八、测试九、安全十、Material设计和 **UX/UI** 六、多线程和并发 Android 中的进程和线程有什么区别? 答:进程是在自己的内存空间中运行的应用程序的单独实例&…...

SpringMVC的异常处理
异常分类 : 预期异常(检查型异常)和运行时异常 1、使用@ExceptionHandle注解处理异常 @ExceptionHandle(value={***.class} 异常类型) public modelandview handelException(){} 仅限当前类使用 2、全局处理方式 @ControllerAdvice + @ExceptionHandle 新建类 @Cont…...

【计算机网络】1 因特网概述
一.网络、互联网和因特网 1.网络(network),由若干结点(node)和连接这些结点的链路(link)组成。 2.多个网络还可以通过路由器互联起来,这样就构成了一个覆盖范围更大的网络…...

【Ubuntu】Anaconda的安装和使用
目录 1 安装 2 使用 1 安装 (1)下载安装包 官网地址:Unleash AI Innovation and Value | Anaconda 点击Free Download 按键。 然后 点击下图中的Download开始下载安装包。 (2)安装 在安装包路径下打开终端&#…...

OpenAI推出首个AI视频模型Sora:重塑视频创作与体验
链接:华为OD机考原题附代码 Sora - 探索AI视频模型的无限可能 随着人工智能技术的飞速发展,AI视频模型已成为科技领域的新热点。而在这个浪潮中,OpenAI推出的首个AI视频模型Sora,以其卓越的性能和前瞻性的技术,引领着…...
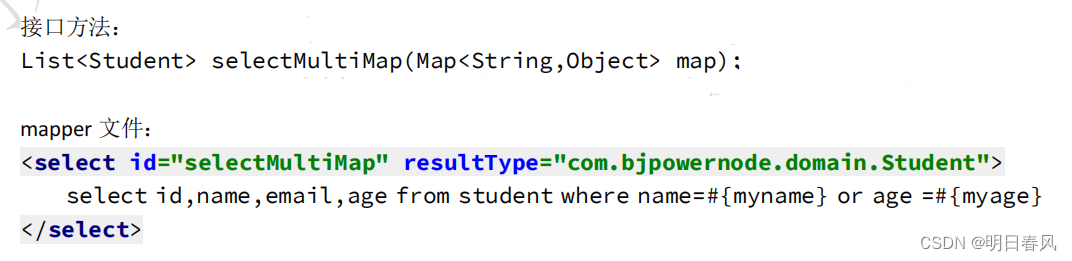
mybatis总结传参三
十、(不推荐)多个参数-按位置传参 参数位置从 0 开始, 引用参数语法 #{ arg 位置 } , 第一个参数是 #{arg0}, 第二个是 #{arg1} 注意: mybatis-3.3 版本和之前的版本使用 #{0},#{1} 方式, 从 myba…...
JSONVUE
1.JSON学习 1.概念: JSON是把JS对象变成字符串. 2.作用: 多用于网络中数据传输. JavaScript对象 let person{name:"张三",age:18}//将JS对象转换为 JSON数据let person2JSON{"name":"张三","age":18}; 3.JS对象与JSON字符串转换…...
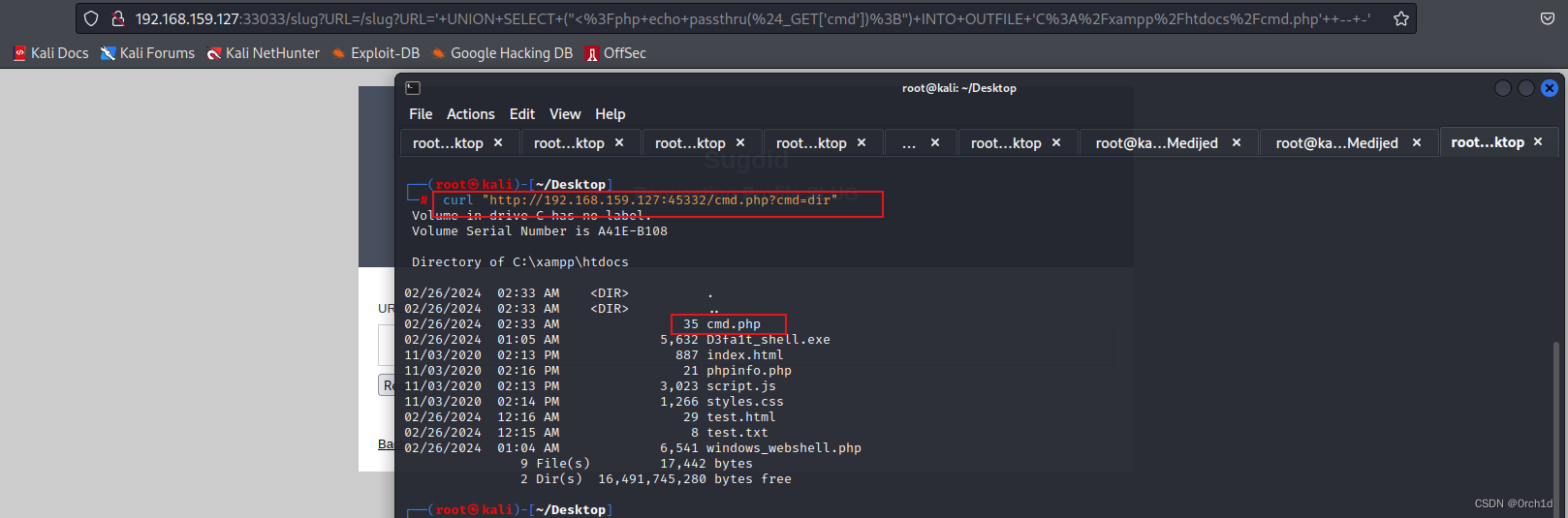
OSCP靶机--Medjed
OSCP靶机–Medjed 考点:(1.ftp文件上传 2.sql注入写shell 3.第三软件提权) 1.nmap ┌──(root㉿kali)-[~/Desktop] └─# nmap 192.168.200.127 -sV -sC -p- --min-rate 5000 Starting Nmap 7.92 ( https://nmap.org ) at 2024-02-25 19:42 EST Nmap scan repo…...
【Unity】Unity与安卓交互
问题描述 Unity和安卓手机进行交互,是我们开发游戏中最常见的场景。本教程将从一个简单的例子来演示一下。 本教程需要用到Android Studio2021.1.1 1.Android Studio新建一个工程 2.选择Empty Activity 然后点击Next 3.点击Finish完成创建 4.选择File-New-New Mo…...

QYFB-02 无线风力报警仪 风速风向超限声光报警
产品概述 无线风力报警仪是由测控报警仪、无线风速风向传感器和太阳能供电盒组成,可观测大气中的瞬时风速,具有风速报警设定和报警输出控制功能;风力报警仪采用无线信号传输、显示屏输出,风速显示采用高亮LED数码管显示ÿ…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...


