算法沉淀——动态规划之子数组、子串系列(上)(leetcode真题剖析)

算法沉淀——动态规划之子数组、子串系列
- 01.最大子数组和
- 02.环形子数组的最大和
- 03.乘积最大子数组
- 04.乘积为正数的最长子数组长度
01.最大子数组和
题目链接:https://leetcode.cn/problems/maximum-subarray/、
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
**进阶:**如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
思路
- 状态表示:
- 使用「经验 + 题目要求」定义线性动态规划的状态表示。
- 选择以「某个位置为结尾」的方式,结合「题目要求」,定义状态表示:dp[i] 表示以 i 位置元素为结尾的「所有子数组」中和的最大和。
- 状态转移方程:
- 将 dp[i] 的所有可能分为两种情况:子数组的长度为 1 或子数组的长度大于 1。
- 如果子数组长度为 1,则 dp[i] = nums[i]。
- 如果子数组长度大于 1,则 dp[i] 应该等于以 i-1 为结尾的「所有子数组」中和的最大值再加上 nums[i],即 dp[i-1] + nums[i]。
- 转移方程为 dp[i] = max(nums[i], dp[i-1] + nums[i])。
- 初始化:
- 在最前面加上一个「辅助结点」,用于初始化。辅助结点的值要保证后续填表是正确的,因此设 dp[0] = 0。
- 辅助结点的存在需要注意下标的映射关系。
- 填表顺序:
- 根据「状态转移方程」,填表顺序为「从左往右」。
- 返回值:
- 状态表 dp 表示以 i 为结尾的所有子数组的最大值,但最大子数组和的结尾是不确定的。因此,返回整个 dp 表中的最大值。
代码
class Solution {
public:int maxSubArray(vector<int>& nums) {int n=nums.size();vector<int> dp(n+1);int ret=INT_MIN;for(int i=1;i<=n;i++){dp[i]=max(nums[i-1],dp[i-1]+nums[i-1]);ret=max(ret,dp[i]);}return ret;}
};
02.环形子数组的最大和
题目链接:https://leetcode.cn/problems/maximum-sum-circular-subarray/
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], ..., nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
示例 1:
输入:nums = [1,-2,3,-2]
输出:3
解释:从子数组 [3] 得到最大和 3
示例 2:
输入:nums = [5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
示例 3:
输入:nums = [3,-2,2,-3]
输出:3
解释:从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
提示:
n == nums.length1 <= n <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104
思路
这个问题与「最大子数组和」的区别在于需要考虑数组首尾相连的情况。结果可能有两种情况:一是在数组的内部,包括整个数组;二是在数组首尾相连的一部分上。
- 对于第一种情况,按照「最大子数组和」的方法得到结果,记为 fmax。
- 对于第二种情况,分析得出,第二种情况的最大和应等于数组总和减去最小子数组和。其中,最小子数组和表示为 gmin。
- 两种情况下的最大值即为所求结果。然而,需要特殊处理数组内全部为负数的情况,因为直接比较两者的最大值可能会得到 0。这种情况下,实际结果应为数组内的最大值。
- 对于「最小子数组和」的求解过程与「最大子数组和」相同,使用 f 表示最大和,g 表示最小和。
- 返回值:先找到 f 表的最大值 fmax;找到 g 表的最小值 gmin;统计所有元素的和 sum;返回 sum == gmin ? fmax : max(fmax, sum - gmin)。
代码
class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {int n=nums.size();vector<int> f(n+1);vector<int> g(n+1);int fmax=INT_MIN,gmin=INT_MAX,sum=0;for(int i=1;i<=n;++i){int x=nums[i-1];sum+=x;f[i]=max(x,x+f[i-1]);fmax=max(fmax,f[i]);g[i]=min(x,x+g[i-1]);gmin=min(gmin,g[i]);}return sum==gmin ? fmax : max(fmax,sum-gmin);}
};
03.乘积最大子数组
题目链接:https://leetcode.cn/problems/maximum-product-subarray/
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 104-10 <= nums[i] <= 10nums的任何前缀或后缀的乘积都 保证 是一个 32-位 整数
思路
这道题类似于「最大子数组和」,但需要考虑乘积而非和。定义两个状态数组 f[i] 和 g[i] 分别表示以 i 为结尾的所有子数组的最大乘积和最小乘积。
- 状态表示:
f[i]表示以 i 为结尾的所有子数组的最大乘积。g[i]表示以 i 为结尾的所有子数组的最小乘积。
- 状态转移方程:
- 对于
f[i],需要考虑三种情况:子数组长度为 1,子数组长度大于 1 且 nums[i] > 0,子数组长度大于 1 且 nums[i] < 0。 - 综上,
f[i] = max(nums[i], max(nums[i] * f[i - 1], nums[i] * g[i - 1]))。 - 对于
g[i],同样考虑三种情况。 - 综上,
g[i] = min(nums[i], min(nums[i] * f[i - 1], nums[i] * g[i - 1]))。
- 对于
- 初始化:
- 在最前面加上一个辅助结点,并设置
f[0] = g[0] = 1。
- 在最前面加上一个辅助结点,并设置
- 填表顺序:
- 从左往右,两个表一起填。
- 返回值:
- 返回
f表中的最大值。
- 返回
代码
class Solution {
public:int maxProduct(vector<int>& nums) {int n=nums.size();vector<int> f(n+1);vector<int> g(n+1);f[0]=g[0]=1;int ret=INT_MIN;for(int i=1;i<=n;++i){int x=nums[i-1],y=f[i-1]*nums[i-1],z=g[i-1]*nums[i-1];f[i]=max(x,max(y,z));g[i]=min(x,min(y,z));ret=max(ret,f[i]);}return ret;}
};
04.乘积为正数的最长子数组长度
题目链接:https://leetcode.cn/problems/maximum-length-of-subarray-with-positive-product/
定一个整数数组nums,找到其中所有元素的乘积为正的子数组的最大长度。
数组的子数组是从该数组中取出的零个或多个值的连续序列。
返回具有正积的子数组的最大长度。
示例1:
输入: nums = [1,-2,-3,4]
输出: 4
解释:数组 nums 的乘积已经为 24。
示例2:
输入: nums = [0,1,-2,-3,-4]
输出: 3
解释:具有正积的最长子数组是 [1,-2,-3],其积为 6。
请注意,我们不能在子数组中包含 0,因为这会使乘积为 0,而 0 不是正数。
示例3:
输入: nums = [-1,-2,-3,0,1]
输出: 2
解释:具有正积的最长子数组是 [-1,-2] 或 [-2,-3]。
限制条件:
1 <= nums.length <= 105-109 <= nums[i] <= 109
思路
1. 状态表达: 定义两个动态规划数组 f 和 g,其中:
f[i]表示以i为结尾的所有子数组中,乘积为正数的最长子数组长度。g[i]表示以i为结尾的所有子数组中,乘积为负数的最长子数组长度。
2. 状态转移方程: 对于 f[i],根据当前元素 nums[i] 的值,分三种情况讨论:
-
如果
nums[i] = 0,说明当前子数组的乘积为零,所以f[i] = 0。 -
如果
nums[i] > 0,说明当前子数组的乘积为正数,直接找到f[i - 1]的值并加一,即f[i] = f[i - 1] + 1。 -
如果
nums[i] < 0,需要根据
g[i - 1]的值来判断:
- 如果
g[i - 1]为零,表示以i - 1为结尾的最长负数子数组不存在,所以f[i] = 0。 - 如果
g[i - 1]不为零,表示以i - 1为结尾的最长负数子数组存在,此时f[i] = g[i - 1] + 1。
- 如果
对于 g[i],也分三种情况讨论:
-
如果
nums[i] = 0,说明当前子数组的乘积为零,所以g[i] = 0。 -
如果
nums[i] < 0,说明当前子数组的乘积为负数,直接找到f[i - 1]的值并加一,即g[i] = f[i - 1] + 1。 -
如果
nums[i] > 0,需要根据
g[i - 1]的值来判断:
- 如果
g[i - 1]为零,表示以i - 1为结尾的最长负数子数组不存在,所以g[i] = 0。 - 如果
g[i - 1]不为零,表示以i - 1为结尾的最长负数子数组存在,此时g[i] = g[i - 1] + 1。
- 如果
3. 初始化: 在数组最前面加上一个辅助结点,设置 f[0] = g[0] = 0。
4. 填表顺序: 从左往右遍历数组,同时填充 f 和 g 两个动态规划数组。
5. 返回值: 返回 f 数组中的最大值,即为最终结果。
代码
class Solution {
public:int getMaxLen(vector<int>& nums) {int n=nums.size();vector<int> f(n+1);vector<int> g(n+1);int ret=INT_MIN;for(int i=1;i<=n;++i){if(nums[i-1]>0){f[i]=f[i-1]+1;g[i]=g[i-1]==0?0:g[i-1]+1;}else if(nums[i-1]<0){f[i]=g[i-1]==0?0:g[i-1]+1;g[i]=f[i-1]+1;}ret=max(ret,f[i]);}return ret;}
};
相关文章:

算法沉淀——动态规划之子数组、子串系列(上)(leetcode真题剖析)
算法沉淀——动态规划之子数组、子串系列 01.最大子数组和02.环形子数组的最大和03.乘积最大子数组04.乘积为正数的最长子数组长度 01.最大子数组和 题目链接:https://leetcode.cn/problems/maximum-subarray/、 给你一个整数数组 nums ,请你找出一个具…...

Flutter GetX 之 暗黑模式
我们紧接上篇文章,今天继续讲解一下强大的 GetX 的另一个功能,就是 暗黑模式 ,在iOS 13开始苹果的应用慢慢的都开始适配 暗黑模式,andr。oid 也慢慢的 开始跟进,截止到目前,商店的大部分应用都已经完成了 暗…...

SQLlabs46关
看看源码 最终我们的id是放到order by后面了 如果我们直接用列去排序 ?sortusername/password username: passward 可以看到顺序是不同的,当然第一列第二列第三列也可以,基本上都是这个原理,那怎么去实现注入呢,我…...
【Android移动开发】Windows10平台安装Android Studio与人工智能算法模型部署案例
目录 一、Android Studio下载地址二、开发环境JDK三、开始安装Android Studio四、案例展示与搭建五、人工智能算法模型移动端部署案例参考 一、Android Studio下载地址 https://developer.android.google.cn/studio/install.html 电脑配置要求: 下载保存在指定文…...
【IDEA】java 项目启动偶现Kotlin 版本问题 error:Kotlin:module was
一、问题描述: error:Kotlin:module was compiled with an incompatible version of kotlin the binary version of its metadata is二、问题原因: jar包版本冲突 三、解决方式: 1、Rebuild Project(推荐☆) 重新构…...
Jmeter系列(2)目录介绍
目录 Jmeter目录介绍bin目录docsextrasliblicensesprintable_docs Jmeter目录介绍 在学习Jmeter之前,需要先对工具的目录有些了解,也会方便后续的学习 bin目录 examplesCSV目录中有CSV样例jmeter.batwindow 启动文件jmeter.shMac/linux的启动文件jmete…...
vue基础操作(vue基础)
想到多少写多少把,其他的想起来了在写。也写了一些css的 input框的双向数据绑定 html <input value"123456" type"text" v-model"account" input"accou" class"bottom-line bottom" placeholder"请输入…...

EEA架构
概念 EEA(Electrical/Electronic Architecture)是一个综合性的概念,它涉及汽车电子电气系统的设计和整合。EEA是汽车上电气部件之间的相互关系,以及包含所有电气部件和电气系统所承载的逻辑功能的组织结构。它是系统的组织结构表…...

【物联网应用案例】牧场牛棚环境管理项目
众所周知,奶牛的健康和牛奶的产量在很大程度上取决于其所在的环境。对于牧场而言,牛棚内的环境更是至关重要。一个适宜的环境不仅能保证奶牛的舒适度,还能提高其产奶量,从而为牧场带来更多的经济效益。 为了更好地理解牛棚环境对…...
【Vue】组件通信组件通信
📝个人主页:五敷有你 🔥系列专栏:JVM ⛺️稳中求进,晒太阳 组件通信 组件通信,就是指组件与组件之间的数据传递 组件的数据是独立的,无法直接访问其他组件的数据想用其他组件的数据--&…...

瑞_Redis_Redis客户端
文章目录 1 Redis客户端1.1 Redis命令行客户端1.2 图形化桌面客户端1.2.1 资源准备1.2.2 安装1.2.3 建立连接 🙊 前言:本文章为瑞_系列专栏之《Redis》的基础篇的Redis客户端章节。由于博主是从B站黑马程序员的《Redis》学习其相关知识,所以本…...
在Ubuntu系统下搭建TDengine集群
目录 一、Ubuntu虚拟机创建 二、系统相关配置 1、设置系统hostname 2、网络配置及IP规划 3、配置FQDN(etc/hosts) 4、服务端口设置 三、TDengine server安装 1、服务安装 2、修改配置 3、启动taosd 4、服务卸载 四、客户端安装 1、client安…...

Easy-Jmeter: 性能测试平台
目录 写在开始1 系统架构2 表结构设计3 测试平台生命周期4 分布式压测5 压力机管理6 用例管理6.1 新增、编辑用例6.2 调试用例6.3 启动测试6.4 动态控量6.5 测试详情6.6 环节日志6.7 实时数据6.8 测试结果 7 测试记录7 用例分析8 系统部署8.1普通部署8.2容器化部署 写在最后 写…...

Unity3D Lua与C#的相互调用与性能剖析详解
前言 在游戏开发中,经常会遇到Lua与C#之间的相互调用的情况。本文将详细介绍Unity3D中Lua与C#的相互调用的方式,并对其性能进行剖析。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀!…...

鸿蒙开发路由跳转踩坑
文章目录 前言常见路由不能跳转问题总结 一、前言 02-25 10:40:10.799 42182-2075594 E C03900/Ace: [manifest_router.cpp(GetPagePath)-(0)] [Engine Log] cant find this page pages 02-25 10:40:10.799 42182-2075594 E C03900/Ace: [page_router_manager.cpp(StartPush…...
SpringBoot 3 新特性
目录 1. GraalVM1.1 生成本地可执行应用1.2 生成docker镜像 2. 支持虚拟线程3. HTTP Interface 1. GraalVM 使用GraalVM将SpringBoot应用程序编译成本地可执行的镜像文件,可以显著提升启动速度、峰值性能以及减少内存应用。传统的应用都是编译成字节码,…...
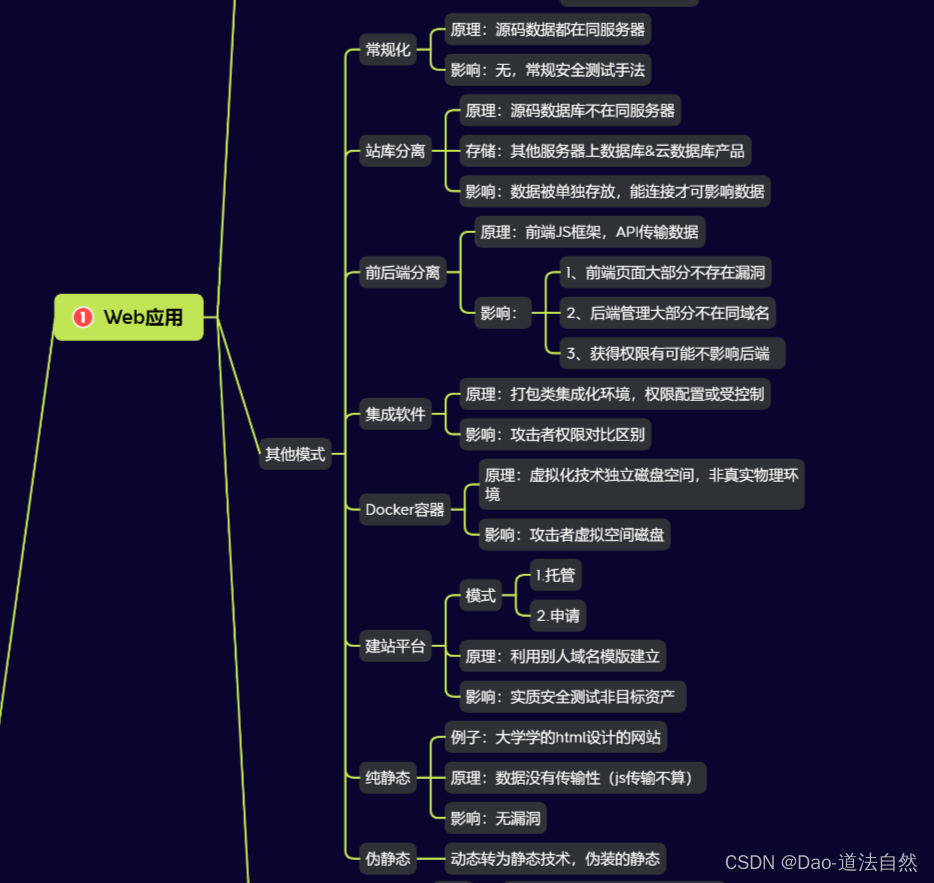
Day02:Web架构前后端分离站Docker容器站集成软件站建站分配
目录 常规化站点部署 站库分离 前后端分离 集成软件搭建Web应用 Docker容器搭建Web应用 建立分配站 静态 与 伪静态 总结 章节知识点: 应用架构:Web/APP/云应用/三方服务/负载均衡等 安全产品:CDN/WAF/IDS/IPS/蜜罐/防火墙/杀毒等 渗…...
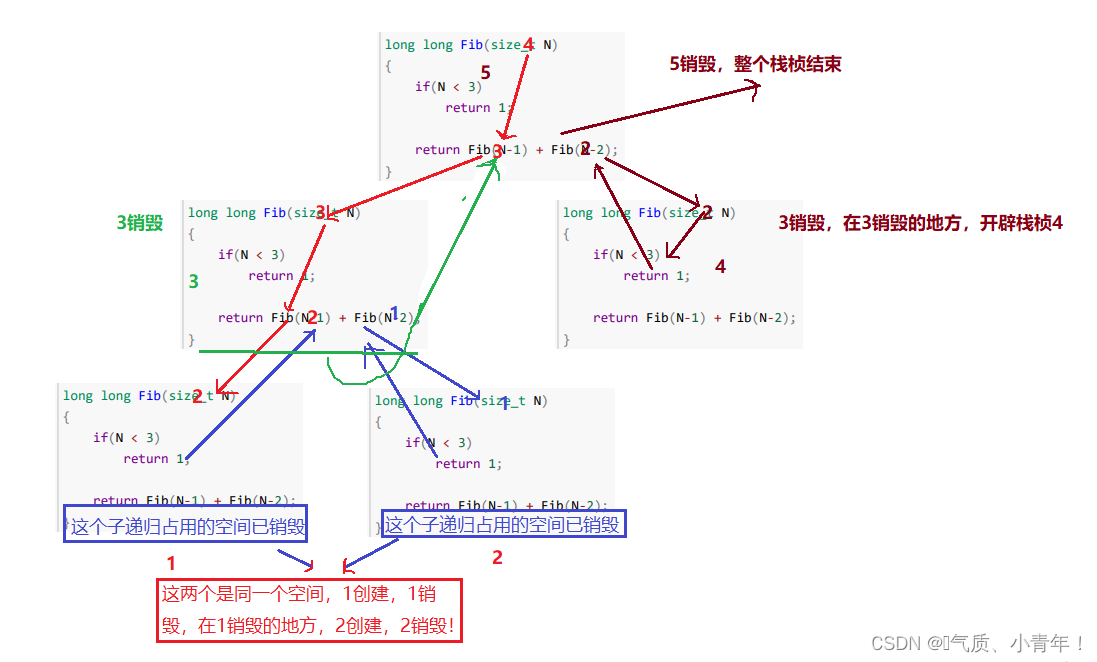
链表和顺序表的优劣分析及其时间、空间复杂度分析
链表和顺序表的优劣分析及其时间、空间复杂度分析 一、链表和顺序表的优劣分析二、算法复杂度<font face "楷体" size 5 color blue>//上面算法的执行次数大致为:F(N) N^22*N10; N 10,F(10) 1002010 130次 N 1…...
QQ防红跳转短网址生成网站完整源码
使用此源码可以生成QQ自动跳转到浏览器的短链接,无视QQ报毒,任意网址均可生成。 全新界面,网站背景图采用Bing随机壁纸 支持生成多种短链接 兼容电脑和手机页面 生成网址记录功能,域名黑名单功能 网站后台可管理数据 安装说明&am…...
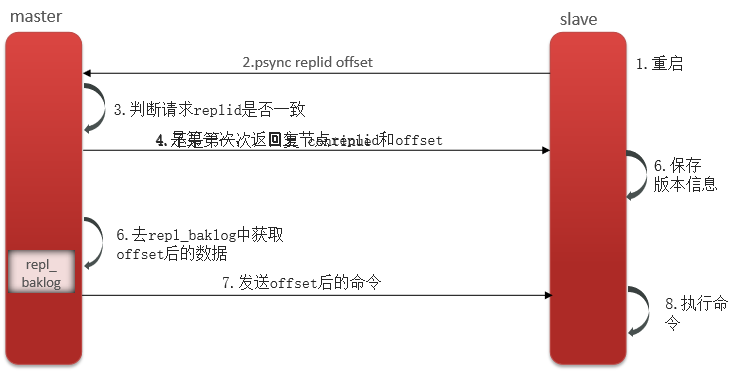
面试redis篇-10Redis集群方案-主从复制
在Redis中提供的集群方案总共有三种: 主从复制哨兵模式分片集群主从复制 单节点Redis的并发能力是有上限的,要进一步提高Redis的并发能力,就需要搭建主从集群,实现读写分离。 主从数据同步原理 Replication Id:简称replid,是数据集的标记,id一致则说明是同一数据集。每…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
