链表和顺序表的优劣分析及其时间、空间复杂度分析
链表和顺序表的优劣分析及其时间、空间复杂度分析
- 一、链表和顺序表的优劣分析
- 二、算法复杂度
- <font face = "楷体" size = 5 color = blue>//上面算法的执行次数大致为:F(N) = N^2+2*N+10; N =10,F(10) = 100+20+10 = 130次 N =100,F(100) = 10000+200+10 = 10210次 N =1000,F(10) = 100000+2000+10 = 1002010次 实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。 </font> <font face = "楷体" size = 5 color = blue>//大O渐进表示法
一、链表和顺序表的优劣分析
1.顺序表的优劣分析
//优势:
//*下标可以随机访问:顺序表的底层是数据,可以下标随机访问!
//CPU高速缓存命中率高(这个还是很重要!)
可以看这篇文章,理解CPU缓存知识!
什么是缓存?
缓存是一种在计算机系统中用于存储数据的硬件或软件组件,它的主要目的是提高数据访问的速度和效率。缓存通常位于CPU内部或主存储器和CPU之间,它能够快速地存储和检索经常访问的数据和指令。当CPU需要访问数据或指令时,它会首先检查缓存中是否已经存在相应的数据或指令,如果存在,则可以直接从缓存中读取,这样就避免了从主存储器中读取数据或指令的延迟。
缓存的设计允许它牺牲数据的实时性,以空间换时间,从而减少数据库的IO操作,减轻服务器压力,减少网络延迟,加快页面打开速度。缓存可以分为不同的层次,如CPU缓存、操作系统文件缓存和浏览器缓存等。
CPU缓存分为L1 Cache(一级缓存)和L2 Cache(二级缓存),它们位于CPU内部,用于存储CPU即将使用的指令和数据。操作系统文件缓存用于存储操作系统读取的文件数据,而浏览器缓存则用于存储用户访问的静态或动态页面内容,以便在用户再次访问时能够快速加载。
总的来说,缓存是一种重要的性能优化技术,它通过将数据存储在更接近处理器或数据源的位置,提高了数据处理的效率和响应速度。
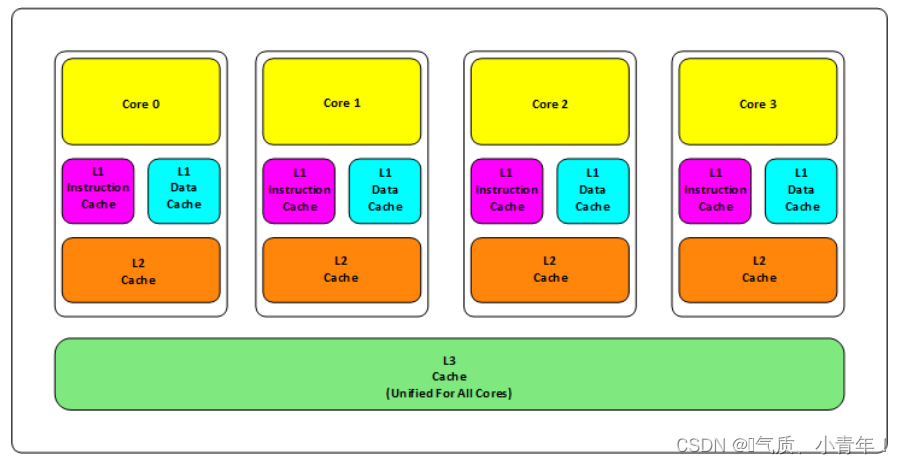
//大概意思是在CPU附近会有三级缓存(L1,L2,L3)
//L1缓存分为两种(指令缓存和数据缓存),L2和L3缓存不分指令和数据
//L1和L2缓存在每一个CPU核中,L3则是所有CPU核心共享的内存。
//L1、L2、L3的越离CPU近就越小,速度也越快,越离CPU远,速度也越慢。
//缓存是速度最快的存储数据的地方
//后面存储数据的地方就是存储器和磁盘
//下面看看各个存储硬件的存储速度
L1 的存取速度:4 个CPU时钟周期
L2 的存取速度:11个CPU时钟周期
L3 的存取速度:39个CPU时钟周期
RAM内存的存取速度:107 个CPU时钟周期
//缓存命中问题!
//我们需要要解一个术语 Cache Line。缓存基本上来说就是把后面的数据加载到离自己近的地方,对于CPU来说,它是不会一个字节一个字节的加载的,因为这非常没有效率,一般来说都是要一块一块的加载的,对于这样的一块一块的数据单位,术语叫“Cache Line”,一般来说,一个主流的CPU的Cache Line 是 64 Bytes(也有的CPU用32Bytes和128Bytes),64Bytes也就是16个32位的整型,这就是CPU从内存中捞数据上来的最小数据单位。
//也就是说CPU在取数据计算的时候至少是取一个缓存行(64Bytes)的大小,这样,顺序表的物理地址连续,加载到缓存中,CPU取到的都是顺序表中存的有效数据,而链表的物理空间不连续,大概率只能取到一个有效数据,其它供CPU计算的数据没用!所谓的缓存命中不高!
//缺点
//前面部分的插入,删除,需要挪动数据,效率低下
//扩容(效率损失,可能还存在一定的空间浪费)
---------------------------------------
2.链表(最优结构的比较)的优劣分析
//优势:
//任意位置的插入,删除效率都很高
//按需申请释放,不存在浪费
//劣势:
//不支持下标随机访问
//CPU高速缓存命中率低(可以理解为 cache line 取数据问题)
二、算法复杂度
//算法在编写成可执行程序后,运行时需要消耗时间资源和(内存)空间资源,衡量一个算法的好坏,要存运行时间的多少和空间消耗大小来衡量一个算法的好坏!!!
//时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
时间复杂度
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个
分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{for (int j = 0; j < N ; ++ j){++count;}
}for (int k = 0; k < 2 * N ; ++ k)
{++count;
}int M = 10;
while (M--)
{++count;
}
//上面算法的执行次数大致为:F(N) = N^2+2*N+10;
N =10,F(10) = 100+20+10 = 130次
N =100,F(100) = 10000+200+10 = 10210次
N =1000,F(10) = 100000+2000+10 = 1002010次
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
//大O渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。 推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。 使用大O的渐进表示法以后,Func1的时间复杂度为:
N= 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界) 例如:在一个长度为N数组中搜索一个数据x 最好情况:1次找到 最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
//考虑最坏情况来写时间复杂度
//上面时间复杂度为:O(N^2)
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
//时间复杂度:O(N)
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}
//时间复杂度:O(M+N)
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
//O(1) --常数次用O(1)表示
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
//冒泡的时间复杂度怎么算?
//这个还是想一下,假设有N个元素,最坏排序多少趟能排好?
// N-1
// N-2
// N-3
// …
// 3
// 2
// 1
//总共执行了多少次?
// (N-1) * (1+N-1)/2 = (N-1) * N/2 = 1/2*(N^2-N);
// 则冒泡排序的时间复杂度:O(N^2)
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}
//二分查找的时间复杂度为多少?
//怎么理解二分查找算法的时间复杂度?
//假设有一个长度为N的数组查找一个数,最坏情况是什么?
//最坏情况是:查找的数只剩一个,或没有,二分查找的实质是每次缩小一半区间来查找!
//查找N个数,则每查找一次,少一半的数
则:N/2/2/2…/2 = 1;区间缩小了多少次?也就是除了多少个2,就是查找了几次!
//设除了x个2
N/(2^x) = 1;
N = 2^x;
x = logN
//所以二分查找算法最坏情况下查找log以2为底N的对数!
//时间复杂度为:O(logN);
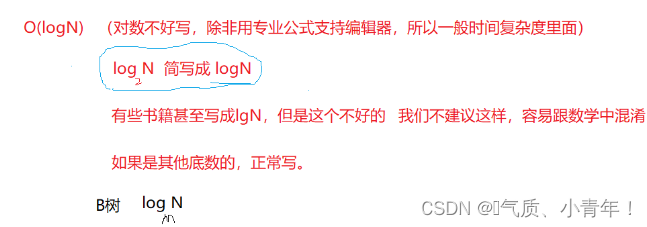
-----------------------------------------
计算下面递归阶乘的时间复杂度?
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}
//所谓的递归多次开辟函数栈桢的过程,那么看一次开辟的栈桢执行程序是多少次,总共N次的递归的时间复杂度!

long long F(size_t N)
{if (0 == N)return 1;for (int i = 0; i < N; i++){//...}return F(N - 1) * N;
}
//计算上面算法的时间复杂度!
//上面函数栈桢开辟了N+1次,每一次是O(N),所以总共是O(N^2)
//总结一下递归算法计算时间复杂度,每次递归子函数消耗累加起来!
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if(N < 3){return 1;}return Fib(N-1) + Fib(N-2);
}
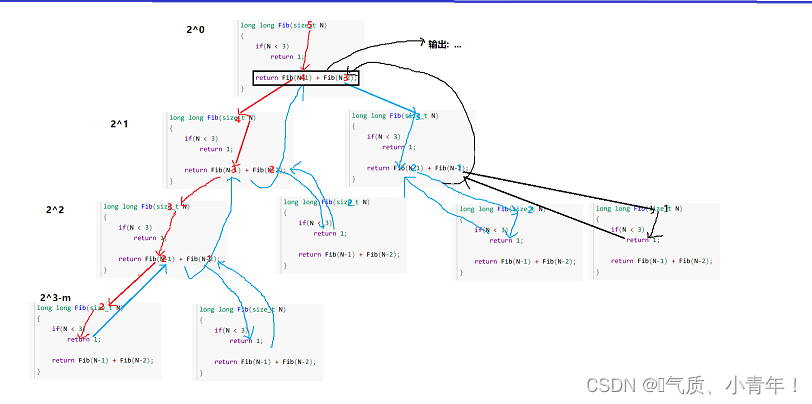
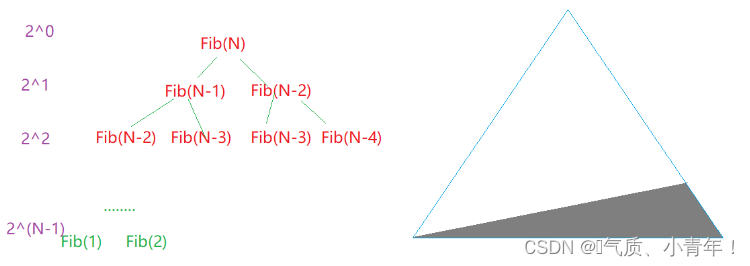

// 2^0
// 2^1
// 2^2
// 2^3
// 2^(N-1)
//: F(n) =2^0 + 2^1 + 2^2 +…+ 2^(N-1)
//:2*F(n) =2^1 + 2^2 + 2^3 +…+ 2^N
//:F(n) = 2^N-1
//:所以斐波那契的时间复杂度:O(2^N)
什么是空间复杂度!
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
//空间复杂度,算的是因为算法的需要,额外开的空间!!!
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0){break;}
}
//在上面的算法中额外开辟的空间变量有:end,i,exchange,说一点在这儿i虽然开辟了n次,但是这儿申请,释放的空间是同一块空间,所以没有额外开辟空间!!!
//所以此算法的空间复杂度是O(N);
-----------------------------------------
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;}
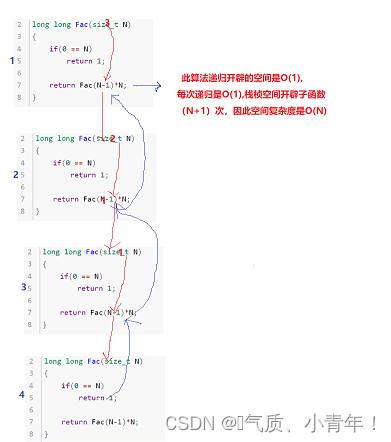
//空间复杂度就是计算算法额外开辟的空间!
//此递归,总共递归了(N+1)次,每次是O(1),总共是O(N);
// 计算斐波那契递归Fib的空间复杂度?
long long Fib(size_t N)
{if(N < 3){return 1;}return Fib(N-1) + Fib(N-2);
//斐波那契递归的空间复杂度怎么算?
//这个比较复杂一点,要理解一点函数栈桢的开辟才能做好!!!
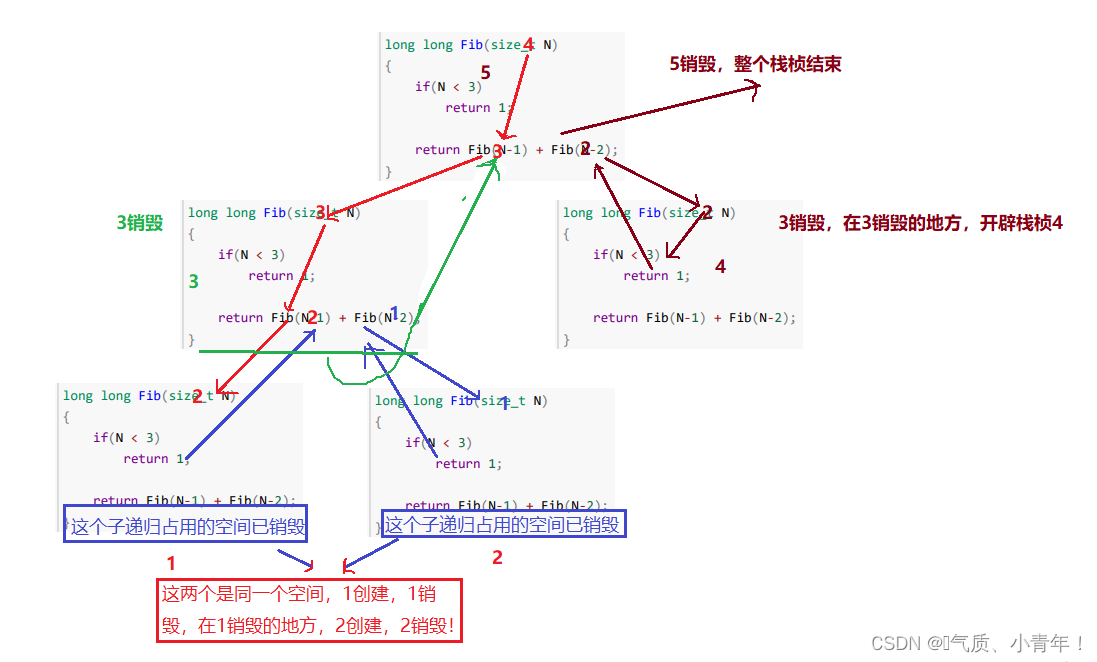
//综上分析:虽然这个递归每一层很复杂,但是利用的空间只有一个子函数的空间,因此斐波那契的空间复杂度是O(N)
完结!!!
相关文章:

链表和顺序表的优劣分析及其时间、空间复杂度分析
链表和顺序表的优劣分析及其时间、空间复杂度分析 一、链表和顺序表的优劣分析二、算法复杂度<font face "楷体" size 5 color blue>//上面算法的执行次数大致为:F(N) N^22*N10; N 10,F(10) 1002010 130次 N 1…...
QQ防红跳转短网址生成网站完整源码
使用此源码可以生成QQ自动跳转到浏览器的短链接,无视QQ报毒,任意网址均可生成。 全新界面,网站背景图采用Bing随机壁纸 支持生成多种短链接 兼容电脑和手机页面 生成网址记录功能,域名黑名单功能 网站后台可管理数据 安装说明&am…...
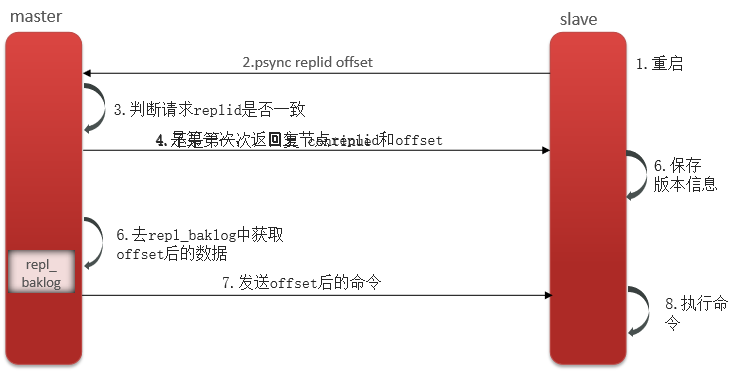
面试redis篇-10Redis集群方案-主从复制
在Redis中提供的集群方案总共有三种: 主从复制哨兵模式分片集群主从复制 单节点Redis的并发能力是有上限的,要进一步提高Redis的并发能力,就需要搭建主从集群,实现读写分离。 主从数据同步原理 Replication Id:简称replid,是数据集的标记,id一致则说明是同一数据集。每…...

【BUG 记录】史诗级 BUG - MYSQL 删库删表却没有备份如何恢复数据
【BUG 记录】史诗级 BUG - MYSQL 删库删表却没有备份如何恢复数据 1. 问题描述2. 解决方案(binlog)2.1 构造测试环境2.2 查看 MySQL 环境是否开启 binlog2.3 查看所有的 binlog 日志记录2.4 查看当前正在使用的是哪一个 binlog 文件2.5 查看此时的 binlo…...
天翼云登录参数JavaSrcipt逆向
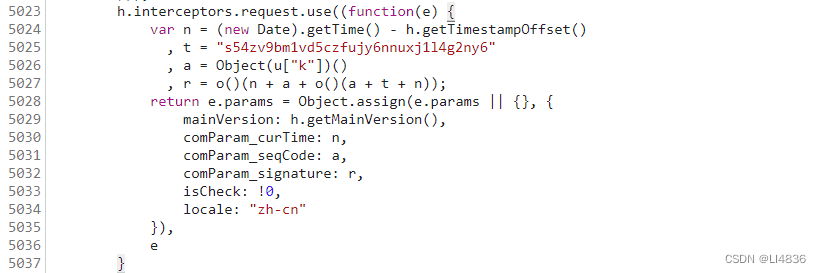
天翼云登录参数 password 、comParam_curTime、comParam_seqCode、comParam_signature JavaSrcipt逆向 目标网站 https://m.ctyun.cn/wap/main/auth/login?redirect/my 目标参数 要逆向的有 password、comParam_curTime、comParam_seqCode、comParam_signature 四个参数 …...

AI与大数据:智慧城市安全的护航者与变革引擎
一、引言 在数字化浪潮的席卷下,智慧城市正成为现代城市发展的新方向。作为城市的神经系统,AI与大数据的融合与应用为城市的安全与应急响应带来了革命性的变革。它们如同城市的“智慧之眼”和“聪明之脑”,不仅为城市管理者提供了强大的决策…...

adb pull 使用
adb pull 是 Android Debug Bridge (ADB) 工具提供的一个命令,用于将设备上的文件拷贝到计算机上。通过 adb pull 命令,实现从 Android 设备上获取文件并保存到本地计算机上。 使用 adb pull 命令的基本语法如下: adb pull <设备路径>…...

算法【线性表的查找-顺序查找】
线性表的查找-顺序查找 顺序查找基本思想应用范围顺序表的表示数据元素类型定义查找算法示例分析 时间效率分析顺序查找的特点如何提高查找效率 顺序查找 基本思想 在表的多种结构定义方式中,线性表是最简单的一种。而顺序查找是线性表查找中最简单的一种。 顺序查…...
力扣1143. 最长公共子序列(动态规划)
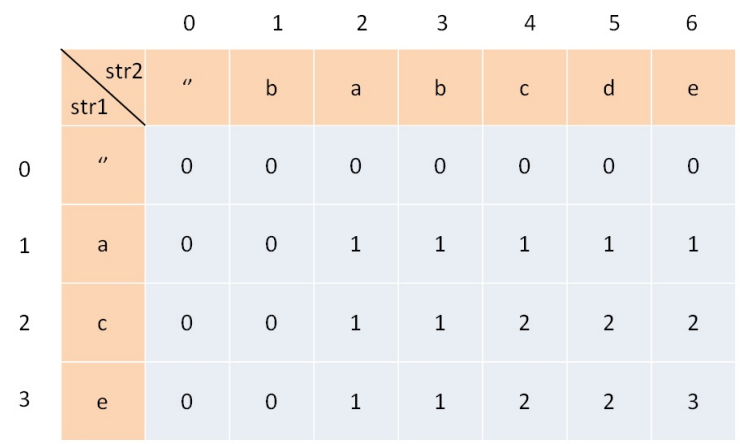
Problem: 1143. 最长公共子序列 文章目录 题目描述思路复杂度Code 题目描述 思路 我们统一标记:str1[i]代表text1表示的字符数组,str2[j]代表text2表示的字符数组;LCS代表最长的公共子序列;(我们易得只有str1[i]和str…...
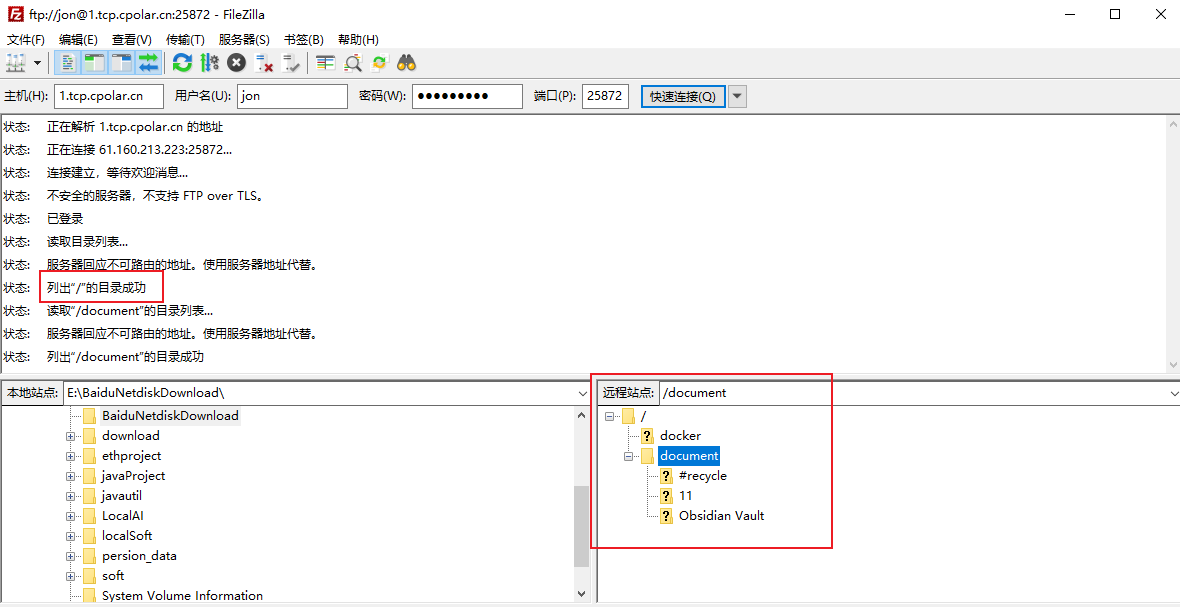
如何使用群晖NAS中FTP服务开启与使用固定地址远程上传下载本地文件?
文章目录 1. 群晖安装Cpolar2. 创建FTP公网地址3. 开启群晖FTP服务4. 群晖FTP远程连接5. 固定FTP公网地址6. 固定FTP地址连接 本文主要介绍如何在群晖NAS中开启FTP服务并结合cpolar内网穿透工具,实现使用固定公网地址远程访问群晖FTP服务实现文件上传下载。 Cpolar内…...

C语言文件知识点
一.解释一些问题 1.标准输入文件(sdtin),通常对应终端的键盘。 2.标准输出文件(stdout)和标准错误输出文件(stderr),这两个文件 都对应终端的屏幕。 (解释:…...

C语言:数组指针 函数指针
C语言:数组指针 & 函数指针 数组指针数组名 数组访问二维数组 函数指针函数指针使用回调函数 typedef关键字 数组指针 数组本质上也是一个变量,那么数组也有自己的地址,指向整个数组的指针,就叫做数组指针。 我先为大家展示…...
全面介绍HTML的语法!轻松写出网页
文章目录 heading(标题)paragraph(段落)link(超链接)imagemap(映射)table(表格)list(列表)layout(分块)form(表单)更多输入:datalistautocompleteautofocusmultiplenovalidatepatternplaceholderrequired head(首部)titlebaselinkstylemetascriptnoscript iframe HTMLÿ…...

数学建模【相关性模型】
一、相关性模型简介 相关性模型并不是指一个具体的模型,而是一类模型,这一类模型用来判断变量之间是否具有相关性。一般来说,分析两个变量之间是否具有相关性,我们根据数据服从的分布和数据所具有的特点选择使用pearsonÿ…...

「优选算法刷题」:字母异位词分组
一、题目 给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的所有字母得到的一个新单词。 示例 1: 输入: strs ["eat", "tea", "tan", "ate", "na…...

【教程】 iOS混淆加固原理篇
目录 摘要 引言 正文 1. 加固的缘由 2. 编译过程 3. 加固类型 1) 字符串混淆 2) 类名、方法名混淆 3) 程序结构混淆加密 4) 反调试、反注入等一些主动保护策略 4. 逆向工具 5. OLLVM 6. IPA guard 7. 代码虚拟化 总结 摘要 本文介绍了iOS应用程序混淆加固的缘由…...

《银幕上的编码传奇:计算机科学与科技精神的光影盛宴》
目录 1.在电影的世界里,计算机科学不仅是一门严谨的学科,更是一种富有戏剧张力和人文思考的艺术载体。 2.电影作为现代文化的重要载体,常常以其丰富的想象力和视觉表现力来探讨计算机科学和技术的各种前沿主题。 3.电影中的程序员角色往往…...
linux提权之sudo风暴
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【Java】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏 …...

数据结构之:跳表
跳表(Skip List)是一种概率性数据结构,它通过在普通有序链表的基础上增加多级索引层来实现快速的查找、插入和删除操作。跳表的效率可以与平衡树相媲美,其操作的时间复杂度也是O(log n),但跳表的结构更简单,…...

matlab 线性四分之一车体模型
1、内容简介 略 57-可以交流、咨询、答疑 路面采用公式积分来获得,计算了车体位移、非悬架位移、动载荷等参数 2、内容说明 略 3、仿真分析 略 线性四分之一车体模型_哔哩哔哩_bilibili 4、参考论文 略...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
