【深度学习笔记】4_6 模型的GPU计算
注:本文为《动手学深度学习》开源内容,部分标注了个人理解,仅为个人学习记录,无抄袭搬运意图
4.6 GPU计算
到目前为止,我们一直在使用CPU计算。对复杂的神经网络和大规模的数据来说,使用CPU来计算可能不够高效。在本节中,我们将介绍如何使用单块NVIDIA GPU来计算。所以需要确保已经安装好了PyTorch GPU版本。准备工作都完成后,下面就可以通过nvidia-smi命令来查看显卡信息了。
!nvidia-smi # 对Linux/macOS用户有效
输出:
Sun Mar 17 14:59:57 2019
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 390.48 Driver Version: 390.48 |
|-------------------------------+----------------------+----------------------+
| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC |
| Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. |
|===============================+======================+======================|
| 0 GeForce GTX 1050 Off | 00000000:01:00.0 Off | N/A |
| 20% 36C P5 N/A / 75W | 1223MiB / 2000MiB | 0% Default |
+-------------------------------+----------------------+----------------------++-----------------------------------------------------------------------------+
| Processes: GPU Memory |
| GPU PID Type Process name Usage |
|=============================================================================|
| 0 1235 G /usr/lib/xorg/Xorg 434MiB |
| 0 2095 G compiz 163MiB |
| 0 2660 G /opt/teamviewer/tv_bin/TeamViewer 5MiB |
| 0 4166 G /proc/self/exe 416MiB |
| 0 13274 C /home/tss/anaconda3/bin/python 191MiB |
+-----------------------------------------------------------------------------+
可以看到我这里只有一块GTX 1050,显存一共只有2000M(太惨了😭)。
4.6.1 计算设备
PyTorch可以指定用来存储和计算的设备,如使用内存的CPU或者使用显存的GPU。默认情况下,PyTorch会将数据创建在内存,然后利用CPU来计算。
用torch.cuda.is_available()查看GPU是否可用:
import torch
from torch import nntorch.cuda.is_available() # 输出 True
查看GPU数量:
torch.cuda.device_count() # 输出 1
查看当前GPU索引号,索引号从0开始:
torch.cuda.current_device() # 输出 0
根据索引号查看GPU名字:
torch.cuda.get_device_name(0) # 输出 'GeForce GTX 1050'
4.6.2 Tensor的GPU计算
默认情况下,Tensor会被存在内存上。因此,之前我们每次打印Tensor的时候看不到GPU相关标识。
x = torch.tensor([1, 2, 3])
x
输出:
tensor([1, 2, 3])
使用.cuda()可以将CPU上的Tensor转换(复制)到GPU上。如果有多块GPU,我们用.cuda(i)来表示第 i i i 块GPU及相应的显存( i i i从0开始)且cuda(0)和cuda()等价。
x = x.cuda(0)
x
输出:
tensor([1, 2, 3], device='cuda:0')
我们可以通过Tensor的device属性来查看该Tensor所在的设备。
x.device
输出:
device(type='cuda', index=0)
我们可以直接在创建的时候就指定设备。
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')x = torch.tensor([1, 2, 3], device=device)
# or
x = torch.tensor([1, 2, 3]).to(device)
x
输出:
tensor([1, 2, 3], device='cuda:0')
如果对在GPU上的数据进行运算,那么结果还是存放在GPU上。
y = x**2
y
输出:
tensor([1, 4, 9], device='cuda:0')
需要注意的是,存储在不同位置中的数据是不可以直接进行计算的。即存放在CPU上的数据不可以直接与存放在GPU上的数据进行运算,位于不同GPU上的数据也是不能直接进行计算的。
z = y + x.cpu()
会报错:
RuntimeError: Expected object of type torch.cuda.LongTensor but found type torch.LongTensor for argument #3 'other'
4.6.3 模型的GPU计算
同Tensor类似,PyTorch模型也可以通过.cuda转换到GPU上。我们可以通过检查模型的参数的device属性来查看存放模型的设备。
net = nn.Linear(3, 1)
list(net.parameters())[0].device
输出:
device(type='cpu')
可见模型在CPU上,将其转换到GPU上:
net.cuda()
list(net.parameters())[0].device
输出:
device(type='cuda', index=0)
同样的,我么需要保证模型输入的Tensor和模型都在同一设备上,否则会报错。
x = torch.rand(2,3).cuda()
net(x)
输出:
tensor([[-0.5800],[-0.2995]], device='cuda:0', grad_fn=<ThAddmmBackward>)
小结
- PyTorch可以指定用来存储和计算的设备,如使用内存的CPU或者使用显存的GPU。在默认情况下,PyTorch会将数据创建在内存,然后利用CPU来计算。
- PyTorch要求计算的所有输入数据都在内存或同一块显卡的显存上。
注:本节与原书此节有一些不同,原书传送门
相关文章:

【深度学习笔记】4_6 模型的GPU计算
注:本文为《动手学深度学习》开源内容,部分标注了个人理解,仅为个人学习记录,无抄袭搬运意图 4.6 GPU计算 到目前为止,我们一直在使用CPU计算。对复杂的神经网络和大规模的数据来说,使用CPU来计算可能不够…...

留学申请过程中如何合理使用AI?大学招生官怎么看?
我们采访过的学生表示,他们在写essay的过程中会使用 ChatGPT,主要用于以下两个方面:第一,生成想法和头脑风暴;第二,拼写和语法检查。 纽约时报的娜塔莎辛格(Natasha Singer)在一篇文…...

vue2与vue3的diff算法有什么区别
在 Vue 中,虚拟 DOM 是一种重要的概念,它通过将真实的 DOM 操作转化为对虚拟 DOM 的操作,从而提高应用的性能。Vue 框架在虚拟 DOM 的更新过程中采用了 Diff 算法,用于比较新旧虚拟节点树,找出需要更新的部分ÿ…...
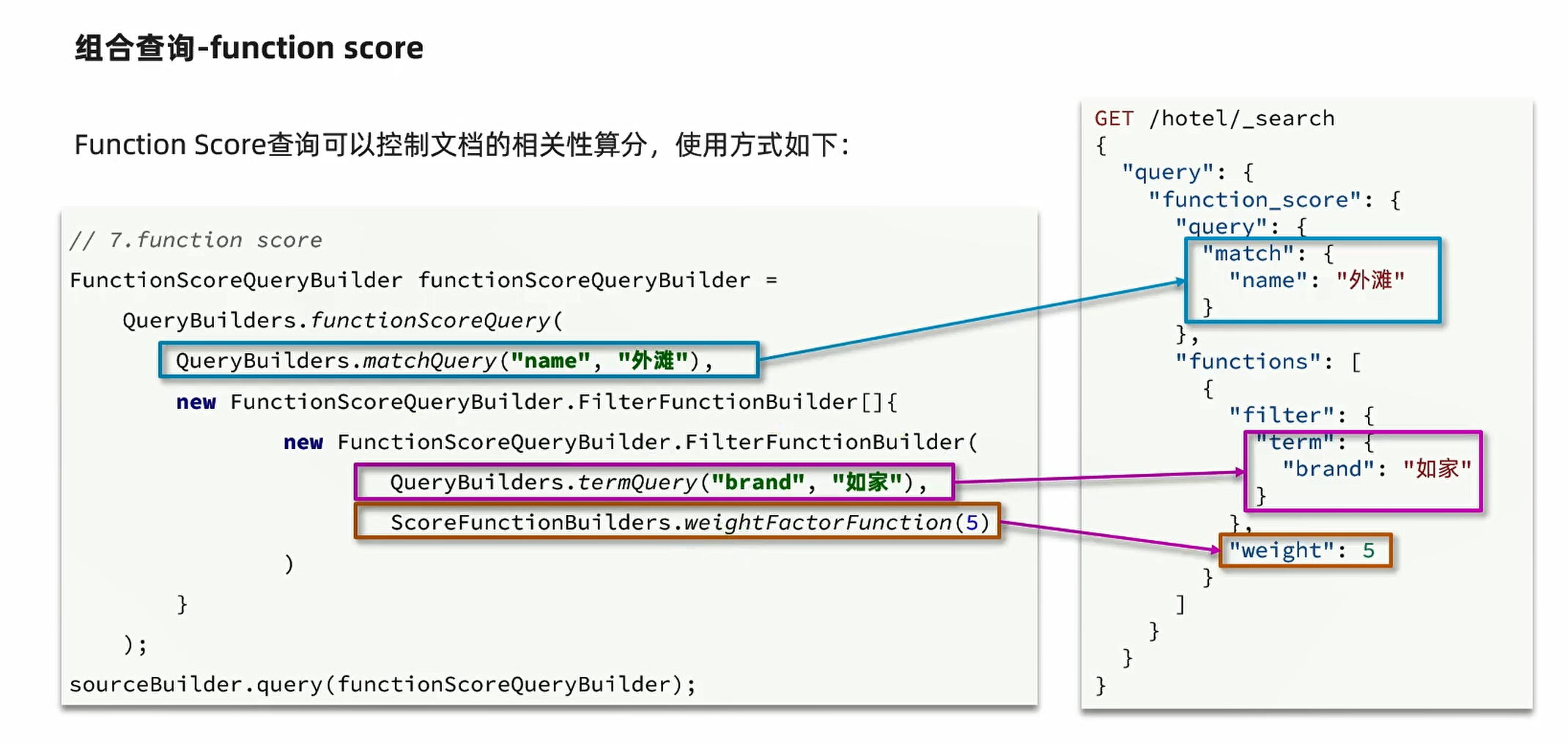
ES小总结
组合查询 FunctionScoreQueryBuilder functionScoreQuery QueryBuilders.functionScoreQuery(boolQuery,new FunctionScoreQueryBuilder.FilterFunctionBuilder[]{new FunctionScoreQueryBuilder.FilterFunctionBuilder(QueryBuilders.termQuery("isAD",true),Score…...

vue2与vue3中父子组件传参的区别
本次主要针对vue中父子组件传参所进行讲解 一、vue2和vue3父传子区别 1.vue2的父传子 1).在父组件子标签中自定义一个属性 <sonPage :子组件接收到的类名"传输的数据">子组件</sonPage> 2).在子组件中peops属性中拿到自定属性 props: {子组件接收的…...

使用vuetify实现全局v-alert消息通知
前排提示,本文为引流文,文章内容不全,更多信息前往:oldmoon.top 查看 简介 使用强大的Vuetify开发前端页面,结果发现官方没有提供简便的全局消息通知组件(像Element中的ElMessage那样)…...

CentOS 7.9上编译wireshark 3.6
工作环境是Centos 7.9,原本是通过flathub安装的wireshark,但是在gnome的application installer上升级到wireshark 4.2.3之后就运行不起来了,flatpak run org.wireshark.Wireshark启动提示缺少qt6,查了一下wireshark新版是依赖qt6的…...

初学学习408之数据结构--数据结构基本概念
初学学习408之数据结构我们先来了解一下数据结构的基本概念。 数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。 本内容来源于参考书籍《大话数据结构》与《王道数据结构》。除去书籍中的内容,作为初学者的我会尽力详细直白地介绍数据结构的…...

Java项目中必须使用本地缓存的几种情况
Java项目中必须使用本地缓存的几种情况 在Java项目的开发过程中,为了提高应用的性能和响应速度,缓存机制经常被使用。其中,本地缓存作为一种常见的缓存方式,将数据存储在应用程序的本地内存或磁盘中,以便快速访问。下…...
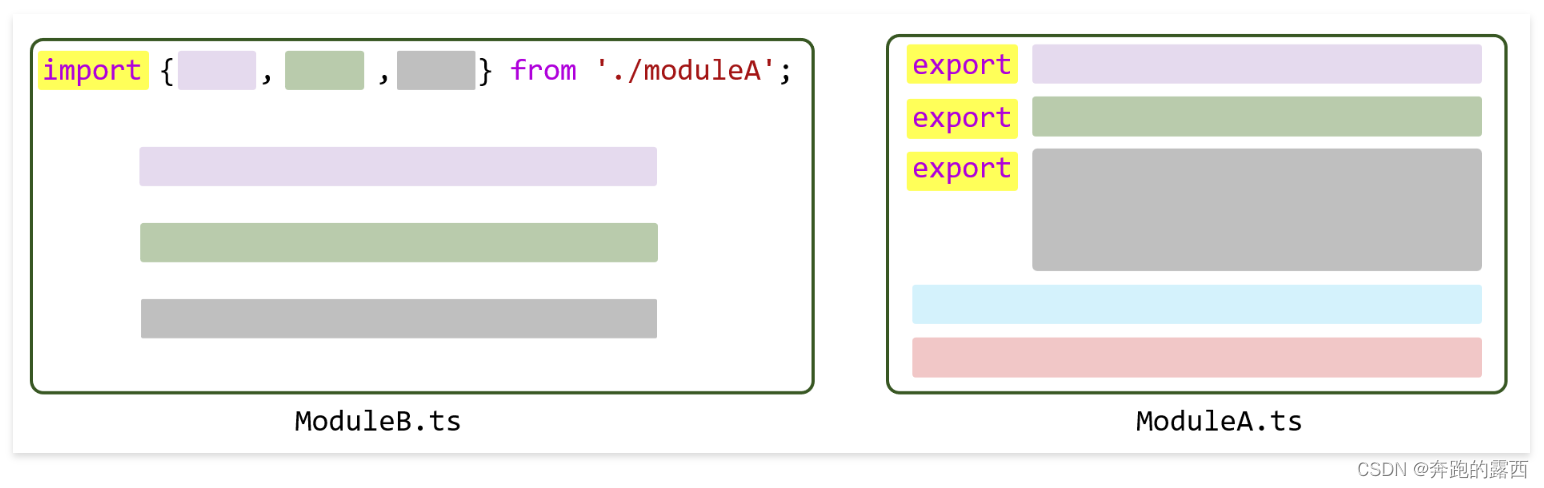
【鸿蒙 HarmonyOS 4.0】TypeScript开发语言
一、背景 HarmonyOS 应用的主要开发语言是 ArkTS,它由 TypeScript(简称TS)扩展而来,在继承TypeScript语法的基础上进行了一系列优化,使开发者能够以更简洁、更自然的方式开发应用。值得注意的是,TypeScrip…...
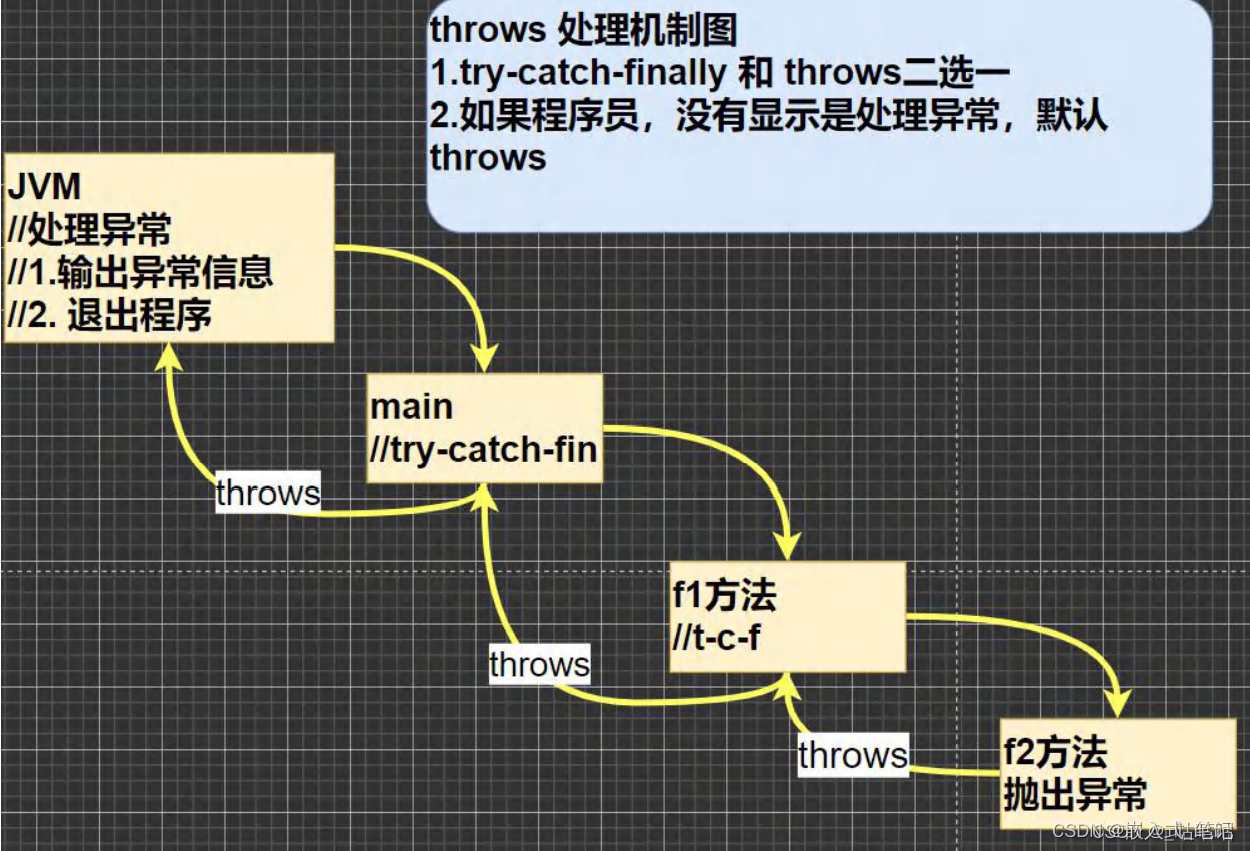
Android java基础_异常
一.异常的概念 在Java中,异常(Exception)是指程序执行过程中可能出现的不正常情况或错误。它是一个事件,它会干扰程序的正常执行流程,并可能导致程序出现错误或崩溃。 异常在Java中是以对象的形式表示的,…...
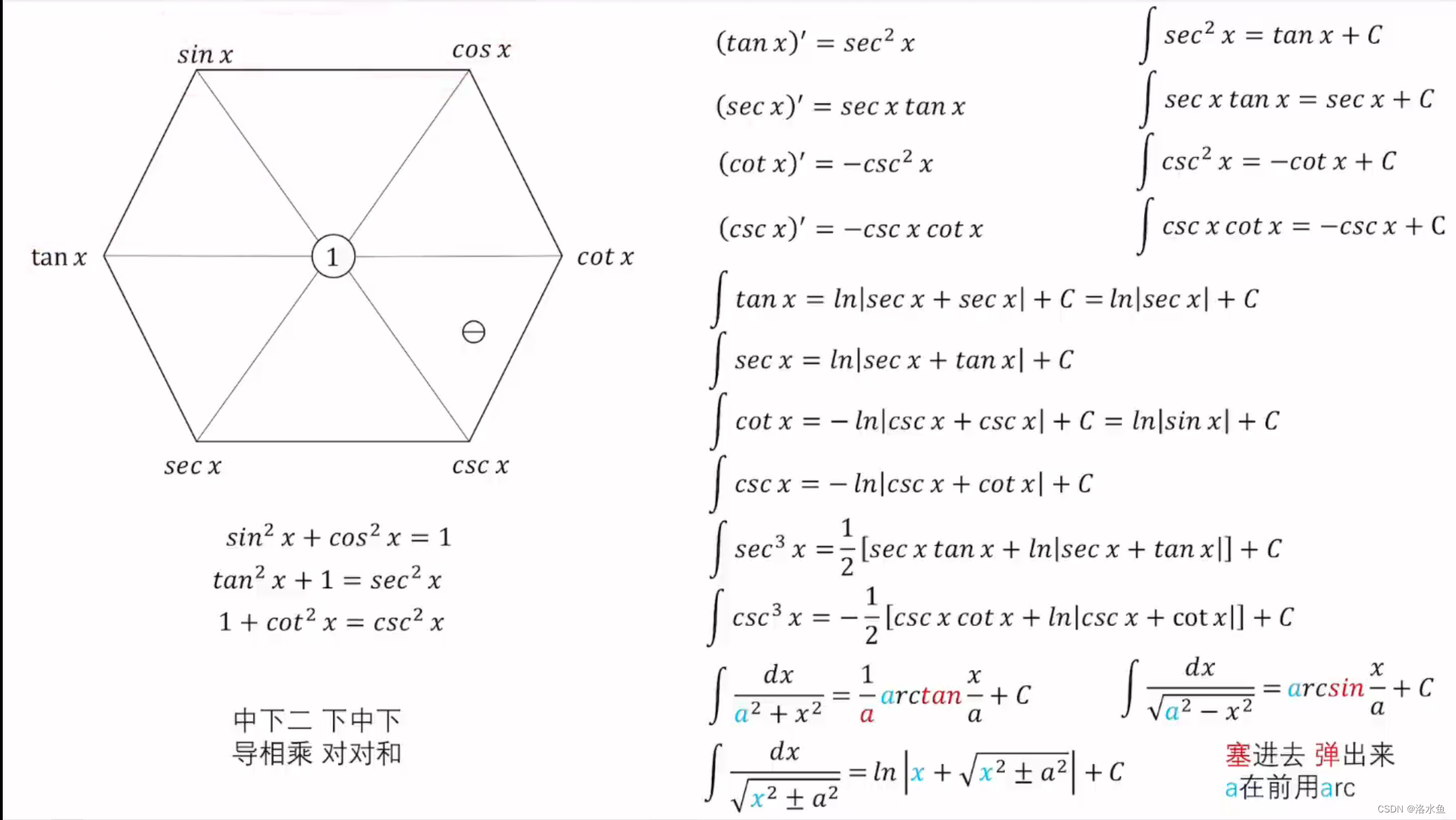
高数考研 -- 公式总结(更新中)
1. 两个重要极限 (1) lim x → 0 sin x x 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}1 limx→0xsinx1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}1 limf(x)→0f(x)sinf(x)1. (2) lim …...

详解顺序结构滑动窗口处理算法
🎀个人主页: https://zhangxiaoshu.blog.csdn.net 📢欢迎大家:关注🔍点赞👍评论📝收藏⭐️,如有错误敬请指正! 💕未来很长,值得我们全力奔赴更美好的生活&…...

Java 8中使用Stream来操作集合
Java 8中使用Stream来操作集合 在Java 8中,你可以使用Stream API来操作集合,这使得集合的处理变得更加简洁和函数式。Stream API提供了一系列的中间操作(intermediate operations)和终端操作(terminal operations&…...

MATLAB环境下一种改进的瞬时频率(IF)估计方法
相对于频率成分单一、周期性强的平稳信号来说,具有非平稳、非周期、非可积特性的非平稳信号更普遍地存在于自然界中。调频信号作为非平稳信号的一种,由于其频率时变、距离分辨率高、截获率低等特性,被广泛应用于雷达、地震勘测等领域。调频信…...

解决:selenium web browser 的版本适配问题
文章目录 解决方案:使用 webdriver manager 自动适配驱动 使用 selenium 操控浏览器的时候报错: The chromedriver version (114.0.5735.90) detected in PATH at /opt/homebrew/bin/chromedriver might not be compatible with the detected chrome ve…...

pytest.param作为pytest.mark.parametrize的参数进行调用
pytest.param:在 pytest.mark.parametrize 中可以作为一个指定的参数进行调用 获取数据库(网页端)数据,通过pytest.param包装成数据包用于pytest.mark.parametrize 中实现数据驱动调用。 import os import pytest import json fr…...
如何判断一个元素是否在可视区域中?
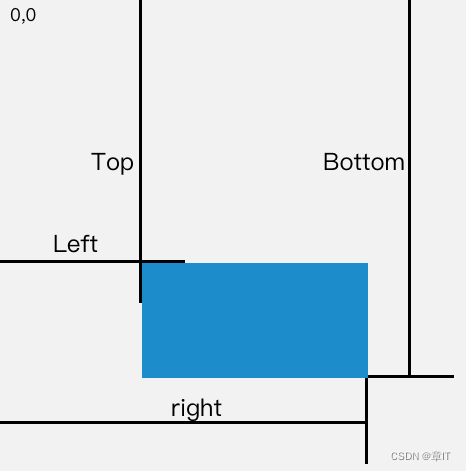
文章目录 一、用途二、实现方式offsetTop、scrollTopgetBoundingClientRectIntersection Observer创建观察者传入被观察者 三、案例分析参考文献 一、用途 可视区域即我们浏览网页的设备肉眼可见的区域,如下图 在日常开发中,我们经常需要判断目标元素是…...

Go Run - Go 语言中的简洁指令
原文:breadchris - 2024.02.21 也许听起来有些傻,但go run是我最喜欢的 Go 语言特性。想要运行你的代码?只需go run main.go。它是如此简单,我可以告诉母亲这个命令,她会立即理解。就像 Go 语言的大部分功能一样&…...
Spring全面精简总结
Spring两大核心功能:IOC控制反转、AOP面向切面的编程 控制反转(loC,Inversion of Control),是一个概念,是一种思想。指将传统上由程序代码直接操控的对象调用权交给容器,通过容器来实现对象的装配和管理。控制反转就是…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
