[算法沉淀记录] 排序算法 —— 堆排序
排序算法 —— 堆排序
算法基础介绍
堆排序(Heap Sort)是一种基于比较的排序算法,它利用堆这种数据结构来实现排序。堆是一种特殊的完全二叉树,其中每个节点的值都必须大于或等于(最大堆)或小于或等于(最小堆)其子节点的值。
基本概念
堆是一个近似完全二叉树的数据结构,满足任一非叶子节点的值不小于(或不大于)其左右孩子节点的值。堆通常分为最大堆和最小堆:
- 最大堆:每个节点的值都大于或等于其子节点的值。
- 最小堆:每个节点的值都小于或等于其子节点的值。
堆排序算法通过构建一个最大堆或最小堆,然后将堆顶元素(最大或最小值)与堆的最后一个元素交换,再将剩余的元素重新调整为最大堆或最小堆,如此反复,直到整个数组有序。
算法步骤
- 构建堆:将无序的输入数组转换为一个最大堆或最小堆。
- 堆排序:
- 将堆顶元素(最大或最小值)与堆的最后一个元素交换,将其移出堆。
- 调整剩余元素,使其重新成为一个最大堆或最小堆。
- 重复上述步骤,直到所有元素都被移出堆。
伪代码描述
function heapsort(array)build_max_heap(array)for end from size(array) down to 2 doswap array[1] with array[end]heap_size = heap_size - 1sift_down(array, 1)end for
end function
堆排序是一种高效的排序算法,具有以下优缺点:
优点
- 时间复杂度稳定:堆排序的时间复杂度为(O(nlog(n))),其中n是数组的长度。这个复杂度在所有比较排序算法中是最优的,因为比较排序的最坏时间复杂度为(O(nlog(n)))。
- 空间复杂度低:堆排序是原地排序,除了常数个额外空间用于存储递归栈之外,不需要额外的内存空间。
- 不稳定的排序算法:堆排序是不稳定的排序算法,这意味着如果两个元素相等,它们的相对顺序在排序后可能会改变。
- 适用于各种数据类型:堆排序可以适用于各种数据类型,包括整数、浮点数、字符串等,只要能够为这些数据类型定义合适的比较操作。
- 易于实现:堆排序的实现相对简单,尤其是使用二叉堆的实现。
缺点
- 最坏情况性能差:虽然平均时间复杂度为(O(nlog(n))),但在最坏情况下(输入数据完全逆序),堆排序的时间复杂度退化为(O(n^2))。
- 不稳定排序:对于某些需要稳定排序的应用场景(如数据库索引),堆排序可能不是最佳选择。
- 对内存要求高:虽然空间复杂度低,但在排序过程中,堆中的元素可能会频繁地移动,这可能导致较高的内存访问开销。
- 初始化堆的时间开销:虽然堆排序的总时间复杂度是(O(nlog(n))),但这个复杂度是在整个排序过程中累积的。在实际应用中,构建初始堆的过程可能会占用一定的时间。
总体而言,堆排序是一个在实际应用中广泛使用的排序算法,特别是当内存使用是一个关键因素时。然而,对于需要稳定排序的应用,或者当数据已经部分有序时,可能需要考虑其他排序算法,如归并排序或快速排序
应用场景
堆排序在实际开发过程中的常见应用场景包括:
- 优先级队列:堆排序是优先级队列实现的基础。在许多编程语言中,优先级队列(或称为最小堆)就是基于堆排序原理实现的。这种数据结构允许快速插入和删除最小元素,常用于任务调度、事件处理等场景。
- 排序算法比较:在开发中,为了验证新算法的性能,开发者可能会将堆排序与其他排序算法(如快速排序、归并排序)进行比较。堆排序因其简单性和稳定性,常作为基准算法之一。
- 数据挖掘:在数据挖掘和机器学习领域,堆排序可用于处理大规模数据集的预处理步骤,如特征选择、频繁项集挖掘等。
- 文件系统:堆排序可用于文件系统的目录排序,帮助用户快速找到文件。
- 数据库索引:虽然数据库通常使用B树或B+树索引,但在某些特殊情况下,堆排序可以作为辅助算法来优化索引的构建过程。
- 缓存管理:在缓存管理系统中,堆排序可用于维护缓存数据的有序性,例如,根据最近最少使用(LRU)策略来淘汰缓存项。
- 算法教学:堆排序是计算机科学教育中常用的教学示例,用于讲解数据结构和算法的概念。
- 图形处理:在图形处理中,堆排序可用于顶点排序,以便于后续的图形操作,如生成凸包、计算几何形状的交点等。
- 游戏开发:在游戏开发中,堆排序可用于实现游戏对象的优先级处理,例如,根据对象的属性(如生命值、攻击力等)对对象进行排序。
- 网络协议:在网络协议处理中,堆排序可用于数据包的优先级处理,确保高优先级的数据包得到优先处理。
堆排序的优点,如时间复杂度的稳定性和低空间复杂度,使其在需要快速、高效处理大规模数据的场景中非常有用。然而,它的不稳定性也是一个需要注意的点,特别是在需要保持数据相对顺序的应用中。
时间复杂度
最佳情况
在最佳情况下,输入数组已经是有序的,堆排序只需要进行一次建堆操作,然后进行一次简单的调整即可完成排序。因此,最佳情况下的时间复杂度是 (O(n))。
最坏情况
在最坏情况下,输入数组是完全逆序的,需要进行 n-1 次建堆操作,并且每次调整堆都需要将堆中的元素重新排列。因此,最坏情况下的时间复杂度是 (O(n^2))。
平均情况
在平均情况下,堆排序的时间复杂度是 (O(nlog(n)))。这是因为虽然最坏情况下的时间复杂度是 (O(n^2)),但在大多数实际应用中,数据并不是完全逆序的,因此平均时间复杂度更接近于 (O(nlog(n)))。
空间复杂度
堆排序是一个原地排序算法,除了用于存储递归栈的常数空间之外,不需要额外的内存空间。因此,空间复杂度是 (O(1))。
证明
时间复杂度证明
- 建堆操作:建堆操作的时间复杂度是 (O(n))。
- 调整堆:调整堆的时间复杂度是 (O(n))。
- 排序过程:排序过程需要进行 n-1 次调整堆的操作。
综合以上,堆排序的总时间复杂度是 (O(n + (n-1) * O(n)) = O(n^2))。
空间复杂度证明
堆排序是一个原地排序算法,除了用于存储递归栈的常数空间之外,不需要额外的内存空间。因此,空间复杂度是 (O(1))。
综上所述,堆排序的时间复杂度在最佳情况下为 (O(n)),最坏情况下为 (O(n^2)),平均情况下为 (O(nlog(n))),空间复杂度为 (O(1))。
代码实现
Python 实现
def heapify(arr, n, i):largest = ileft = 2 * i + 1right = 2 * i + 2if left < n and arr[i] < arr[left]:largest = leftif right < n and arr[largest] < arr[right]:largest = rightif largest != i:arr[i], arr[largest] = arr[largest], arr[i]heapify(arr, n, largest)def heapsort(arr):n = len(arr)for i in range(n//2 - 1, -1, -1):heapify(arr, n, i)for i in range(n-1, 0, -1):arr[i], arr[0] = arr[0], arr[i]heapify(arr, i, 0)
C++ 模板实现
Java 实现
扩展阅读
堆排序的时间复杂度优化主要集中在减少建堆和调整堆的次数上。以下是一些常见的优化方法:
时间复杂度的优化方法
- 减少比较次数:通过减少不必要的比较,可以减少建堆和调整堆的时间。例如,可以使用二叉堆的路径压缩技术,在调整堆的过程中减少子节点与父节点的比较次数。
- 使用斐波那契堆:斐波那契堆是一种数据结构,它可以在O(log n)的时间内完成堆的插入、删除和合并操作。这比二叉堆的O(log n)复杂度更优。
- 延迟删除:在某些实现中,为了避免频繁地调整堆,可以延迟删除操作,直到需要的时候才进行。
- 减少调整堆的次数:通过选择合适的堆大小和调整策略,可以减少调整堆的次数。
历史上常用的堆排序的变种算法
- 斐波那契堆:斐波那契堆是一种改进的堆数据结构,它可以在O(log n)的时间内完成堆的插入、删除和合并操作,比二叉堆更优。
- 二叉堆:二叉堆是最常见的堆实现,它包括最大堆和最小堆。二叉堆的调整操作通常需要O(log n)的时间复杂度。
- 左倾堆:左倾堆是一种特殊的堆实现,它通过减少堆的平衡调整次数来优化性能。
- 二项堆:二项堆是一种特殊的堆实现,它使用二项树的性质来优化堆的插入和删除操作。
- 二叉索引堆:二叉索引堆是一种结合了二叉堆和二叉树索引的数据结构,它可以在O(log n)的时间内完成堆的插入、删除和合并操作。
这些变种算法的目的是通过优化堆的实现细节,减少堆排序的时间复杂度,使其在实际应用中更加高效。在选择堆排序的变种算法时,需要考虑数据的特点和应用场景,以确定最适合的算法。
斐波那契堆排序
斐波那契堆排序(Fibonacci Heap Sort)是一种堆排序的变种,由Michael L. Fredman, Robert Sedgewick, Daniel D. Sleator, 和Robert E. Tarjan在1986年提出。斐波那契堆是一种数据结构,它提供了一种堆操作的实现,这些操作包括插入、删除最小元素、删除最小元素的父节点等,其时间复杂度几乎都是O(log n)。
基本概念
斐波那契堆是一种堆数据结构,它支持以下操作:
- 插入:将一个元素添加到堆中。
- 删除最小元素:移除堆中的最小元素。
- 删除最小元素的父节点:移除并返回堆中与最小元素具有相同父节点的最小元素。
- 合并:将两个斐波那契堆合并成一个堆。
斐波那契堆通过减少堆的平衡调整次数来优化性能。在斐波那契堆中,插入和删除操作通常需要O(log n)的时间复杂度,而传统的二叉堆通常需要O(log n)的复杂度。
算法步骤
斐波那契堆排序的基本步骤如下:
- 初始化:创建一个空的斐波那契堆。
- 插入元素:将所有待排序的元素插入到斐波那契堆中。
- 删除最小元素:重复执行以下操作,直到堆中只剩下一个元素:
- 删除并返回堆中的最小元素。
- 将删除元素的后继节点(如果有)插入到堆中。
- 排序完成:最后剩下的元素是排序后的第一个元素。
伪代码描述
斐波那契堆排序(A)创建一个空的斐波那契堆对于每个元素x in A插入(斐波那契堆, x)while 斐波那契堆中元素数量 > 1删除并返回最小元素(斐波那契堆)将删除元素的后继节点插入(斐波那契堆)返回堆中剩下的元素
Python 代码实现
class FibonacciHeap:# internal node classclass Node:def __init__(self, key, value):self.key = keyself.value = valueself.parent = self.child = self.left = self.right = Noneself.degree = 0self.mark = False# function to iterate through a doubly linked listdef iterate(self, head):node = stop = headflag = Falsewhile True:if node == stop and flag is True:breakelif node == stop:flag = Trueyield nodenode = node.right# pointer to the head and minimum node in the root listroot_list, min_node = None, None# maintain total node count in full fibonacci heaptotal_nodes = 0# return min node in O(1) timedef find_min(self):return self.min_node# extract (delete) the min node from the heap in O(log n) time# amortized cost analysis can be found here (http://bit.ly/1ow1Clm)def extract_min(self):z = self.min_nodeif z is not None:if z.child is not None:# attach child nodes to root listchildren = [x for x in self.iterate(z.child)]for i in range(0, len(children)):self.merge_with_root_list(children[i])children[i].parent = Noneself.remove_from_root_list(z)# set new min node in heapif z == z.right:self.min_node = self.root_list = Noneelse:self.min_node = z.rightself.consolidate()self.total_nodes -= 1return z# insert new node into the unordered root list in O(1) time# returns the node so that it can be used for decrease_key laterdef insert(self, key, value=None):n = self.Node(key, value)n.left = n.right = nself.merge_with_root_list(n)if self.min_node is None or n.key < self.min_node.key:self.min_node = nself.total_nodes += 1return n# modify the key of some node in the heap in O(1) timedef decrease_key(self, x, k):if k > x.key:return Nonex.key = ky = x.parentif y is not None and x.key < y.key:self.cut(x, y)self.cascading_cut(y)if x.key < self.min_node.key:self.min_node = x# merge two fibonacci heaps in O(1) time by concatenating the root lists# the root of the new root list becomes equal to the first list and the second# list is simply appended to the end (then the proper min node is determined)def merge(self, h2):H = FibonacciHeap()H.root_list, H.min_node = self.root_list, self.min_node# fix pointers when merging the two heapslast = h2.root_list.lefth2.root_list.left = H.root_list.leftH.root_list.left.right = h2.root_listH.root_list.left = lastH.root_list.left.right = H.root_list# update min node if neededif h2.min_node.key < H.min_node.key:H.min_node = h2.min_node# update total nodesH.total_nodes = self.total_nodes + h2.total_nodesreturn H# if a child node becomes smaller than its parent node we# cut this child node off and bring it up to the root listdef cut(self, x, y):self.remove_from_child_list(y, x)y.degree -= 1self.merge_with_root_list(x)x.parent = Nonex.mark = False# cascading cut of parent node to obtain good time boundsdef cascading_cut(self, y):z = y.parentif z is not None:if y.mark is False:y.mark = Trueelse:self.cut(y, z)self.cascading_cut(z)# combine root nodes of equal degree to consolidate the heap# by creating a list of unordered binomial treesdef consolidate(self):A = [None] * int(math.log(self.total_nodes) * 2)nodes = [w for w in self.iterate(self.root_list)]for w in range(0, len(nodes)):x = nodes[w]d = x.degreewhile A[d] != None:y = A[d]if x.key > y.key:temp = xx, y = y, tempself.heap_link(y, x)A[d] = Noned += 1A[d] = x# find new min node - no need to reconstruct new root list below# because root list was iteratively changing as we were moving# nodes around in the above loopfor i in range(0, len(A)):if A[i] is not None:if A[i].key < self.min_node.key:self.min_node = A[i]# actual linking of one node to another in the root list# while also updating the child linked listdef heap_link(self, y, x):self.remove_from_root_list(y)y.left = y.right = yself.merge_with_child_list(x, y)x.degree += 1y.parent = xy.mark = False# merge a node with the doubly linked root listdef merge_with_root_list(self, node):if self.root_list is None:self.root_list = nodeelse:node.right = self.root_list.rightnode.left = self.root_listself.root_list.right.left = nodeself.root_list.right = node# merge a node with the doubly linked child list of a root nodedef merge_with_child_list(self, parent, node):if parent.child is None:parent.child = nodeelse:node.right = parent.child.rightnode.left = parent.childparent.child.right.left = nodeparent.child.right = node# remove a node from the doubly linked root listdef remove_from_root_list(self, node):if node == self.root_list:self.root_list = node.rightnode.left.right = node.rightnode.right.left = node.left# remove a node from the doubly linked child listdef remove_from_child_list(self, parent, node):if parent.child == parent.child.right:parent.child = Noneelif parent.child == node:parent.child = node.rightnode.right.parent = parentnode.left.right = node.rightnode.right.left = node.leftdef fibonacci_heap_sort(arr):heap = FibonacciHeap()for key in arr:heap.insert(key)sorted_arr = []while heap.total_nodes > 0:sorted_arr.append(heap.extract_min().key)return sorted_arr
C++模板代码实现
template <class V>
class FibonacciHeap;template <class V>
struct node
{
private:node<V> *prev;node<V> *next;node<V> *child;node<V> *parent;V value;int degree;bool marked;public:friend class FibonacciHeap<V>;node<V> *getPrev() { return prev; }node<V> *getNext() { return next; }node<V> *getChild() { return child; }node<V> *getParent() { return parent; }V getValue() { return value; }bool isMarked() { return marked; }bool hasChildren() { return child; }bool hasParent() { return parent; }
};template <class V>
class FibonacciHeap
{
protected:node<V> *heap;public:FibonacciHeap(){heap = _empty();}virtual ~FibonacciHeap(){if (heap){_deleteAll(heap);}}node<V> *insert(V value){node<V> *ret = _singleton(value);heap = _merge(heap, ret);return ret;}void merge(FibonacciHeap &other){heap = _merge(heap, other.heap);other.heap = _empty();}bool isEmpty(){return heap == nullptr;}V getMinimum(){return heap->value;}V removeMinimum(){node<V> *old = heap;heap = _removeMinimum(heap);V ret = old->value;delete old;return ret;}void decreaseKey(node<V> *n, V value){heap = _decreaseKey(heap, n, value);}node<V> *find(V value){return _find(heap, value);}private:node<V> *_empty(){return nullptr;}node<V> *_singleton(V value){node<V> *n = new node<V>;n->value = value;n->prev = n->next = n;n->degree = 0;n->marked = false;n->child = nullptr;n->parent = nullptr;return n;}node<V> *_merge(node<V> *a, node<V> *b){if (a == nullptr)return b;if (b == nullptr)return a;if (a->value > b->value){node<V> *temp = a;a = b;b = temp;}node<V> *an = a->next;node<V> *bp = b->prev;a->next = b;b->prev = a;an->prev = bp;bp->next = an;return a;}void _deleteAll(node<V> *n){if (n != nullptr){node<V> *c = n;do{node<V> *d = c;c = c->next;_deleteAll(d->child);delete d;} while (c != n);}}void _addChild(node<V> *parent, node<V> *child){child->prev = child->next = child;child->parent = parent;parent->degree++;parent->child = _merge(parent->child, child);}void _unMarkAndUnParentAll(node<V> *n){if (n == nullptr)return;node<V> *c = n;do{c->marked = false;c->parent = nullptr;c = c->next;} while (c != n);}node<V> *_removeMinimum(node<V> *n){_unMarkAndUnParentAll(n->child);if (n->next == n){n = n->child;}else{n->next->prev = n->prev;n->prev->next = n->next;n = _merge(n->next, n->child);}if (n == nullptr)return n;node<V> *trees[64] = {nullptr};while (true){if (trees[n->degree] != nullptr){node<V> *t = trees[n->degree];if (t == n)break;trees[n->degree] = nullptr;if (n->value < t->value){t->prev->next = t->next;t->next->prev = t->prev;_addChild(n, t);}else{t->prev->next = t->next;t->next->prev = t->prev;if (n->next == n){t->next = t->prev = t;_addChild(t, n);n = t;}else{n->prev->next = t;n->next->prev = t;t->next = n->next;t->prev = n->prev;_addChild(t, n);n = t;}}continue;}else{trees[n->degree] = n;}n = n->next;}node<V> *min = n;node<V> *start = n;do{if (n->value < min->value)min = n;n = n->next;} while (n != start);return min;}node<V> *_cut(node<V> *heap, node<V> *n){if (n->next == n){n->parent->child = nullptr;}else{n->next->prev = n->prev;n->prev->next = n->next;n->parent->child = n->next;}n->next = n->prev = n;n->marked = false;return _merge(heap, n);}node<V> *_decreaseKey(node<V> *heap, node<V> *n, V value){if (n->value < value)return heap;n->value = value;if (n->parent){if (n->value < n->parent->value){heap = _cut(heap, n);node<V> *parent = n->parent;n->parent = nullptr;while (parent != nullptr && parent->marked){heap = _cut(heap, parent);n = parent;parent = n->parent;n->parent = nullptr;}if (parent != nullptr && parent->parent != nullptr)parent->marked = true;}}else{if (n->value < heap->value){heap = n;}}return heap;}node<V> *_find(node<V> *heap, V value){node<V> *n = heap;if (n == nullptr)return nullptr;do{if (n->value == value)return n;node<V> *ret = _find(n->child, value);if (ret)return ret;n = n->next;} while (n != heap);return nullptr;}
};template <class T>
void FibonacciHeapSort(vector<T> &data)
{FibonacciHeap<T> heap;auto dataSize = data.size();for (auto i = 0; i < dataSize; i++)heap.insert(data[i]);for (auto i = 0; i < dataSize; i++)data[i] = heap.removeMinimum();
}
二叉堆排序
二叉堆排序是一种基于比较的排序算法,它利用二叉堆这种数据结构来进行排序。二叉堆是一种特殊的堆,它是一个近似完全二叉树,满足任一非叶子节点的值不大于或不小于其左右孩子节点的值。根据堆的这一特性,二叉堆分为最大堆和最小堆。在最大堆中,每个父节点的值都大于或等于其孩子节点的值;在最小堆中,每个父节点的值都小于或等于其孩子节点的值。
基本概念
- 二叉堆的性质:对于最大堆,每个父节点的值都大于或等于其孩子节点的值;对于最小堆,每个父节点的值都小于或等于其孩子节点的值。
- 堆的表示:通常使用数组来表示堆,对于任意节点i(假设数组从1开始索引),其左孩子为2i,右孩子为2i+1,父节点为i/2(向下取整)。
算法步骤
- 构建堆:将无序数组构造成一个最大堆(或最小堆)。
- 调整堆:将堆顶元素(最大或最小值)与数组末尾元素交换,然后调整堆,使其满足堆的性质。
- 重复调整:重复步骤2,直到堆中只剩下一个元素,此时数组已排序。
伪代码
二叉堆排序(array):构建最大堆(array)for i = length(array) downto 2:交换array[1]和array[i]调整堆(array, 1, i - 1)end for
end 二叉堆排序
构建最大堆(array):n = length(array)for i = n/2 downto 1:调整堆(array, i, n)end for
end 构建最大堆
调整堆(array, i, n):while 2*i <= n:j = 2*iif j + 1 <= n and array[j] < array[j + 1]:j = j + 1if array[i] < array[j]:交换array[i]和array[j]i = jelse:breakend while
end 调整堆
Python代码实现
class MaxHeap:def __init__(self):self.heap = []def parent(self, i):return (i - 1) // 2def left_child(self, i):return 2 * i + 1def right_child(self, i):return 2 * i + 2def has_left_child(self, i):return self.left_child(i) < len(self.heap)def has_right_child(self, i):return self.right_child(i) < len(self.heap)def swap(self, i, j):self.heap[i], self.heap[j] = self.heap[j], self.heap[i]def heapify_up(self, i):while i > 0 and self.heap[self.parent(i)] < self.heap[i]:self.swap(i, self.parent(i))i = self.parent(i)def heapify_down(self, i):largest = iif self.has_left_child(i) and self.heap[self.left_child(i)] > self.heap[largest]:largest = self.left_child(i)if self.has_right_child(i) and self.heap[self.right_child(i)] > self.heap[largest]:largest = self.right_child(i)if largest != i:self.swap(i, largest)self.heapify_down(largest)def insert(self, key):self.heap.append(key)self.heapify_up(len(self.heap) - 1)def extract_max(self):if len(self.heap) == 0:return Nonemax_value = self.heap[0]self.heap[0] = self.heap[-1]self.heap.pop()self.heapify_down(0)return max_valuedef build_heap(self, arr):self.heap = arr.copy()for i in range(len(self.heap) // 2, -1, -1):self.heapify_down(i)def is_empty(self):return len(self.heap) == 0def get_max(self):if self.is_empty():return Nonereturn self.heap[0]def __str__(self):return str(self.heap)def max_heap_sort(arr):max_heap = MaxHeap()max_heap.build_heap(arr)sorted_arr = []while not max_heap.is_empty():sorted_arr.append(max_heap.extract_max())return sorted_arr[::-1] # Reverse to get ascending order
C++模板实现
#include <iostream>
#include <vector>
#include <algorithm>template <typename T>
void maxHeapify(std::vector<T>& arr, int i, int n) {int left = 2 * i + 1;int right = 2 * i + 2;int largest = i;if (left < n && arr[left] > arr[largest]) {largest = left;}if (right < n && arr[right] > arr[largest]) {largest = right;}if (largest != i) {std::swap(arr[i], arr[largest]);maxHeapify(arr, largest, n);}
}template <typename T>
void heapSort(std::vector<T>& arr) {int n = arr.size();// Build max heapfor (int i = n / 2 - 1; i >= 0; i--) {maxHeapify(arr, i, n);}// Extract elements from heapfor (int i = n - 1; i >= 0; i--) {std::swap(arr[0], arr[i]);maxHeapify(arr, 0, i);}
}
这段代码首先定义了一个maxHeapify函数,用于调整堆,使其满足最大堆的性质。然后定义了heapSort函数,该函数首先构建一个最大堆,然后通过不断将堆顶元素与数组末尾元素交换并调整堆,实现了排序。最后在main函数中测试了排序算法。
二叉堆实现
template <typename T>
class BinaryHeap
{
private:vector<T> heap;// 用于将新插入的元素上浮到正确位置void siftUp(int index){while (index > 0 && heap[(index - 1) / 2] < heap[index]){swap(heap[index], heap[(index - 1) / 2]);index = (index - 1) / 2;}}// 用于将堆顶元素下沉到正确位置void siftDown(int index){int left = 2 * index + 1;int right = 2 * index + 2;int largest = index;if (left < heap.size() && heap[left] > heap[largest]){largest = left;}if (right < heap.size() && heap[right] > heap[largest]){largest = right;}if (largest != index){swap(heap[index], heap[largest]);siftDown(largest);}}public:BinaryHeap() {}// 插入元素void insert(T value){heap.push_back(value);siftUp(heap.size() - 1);}// 删除堆顶元素void remove(){if (heap.empty()){return;}heap[0] = heap.back();heap.pop_back();if (!heap.empty()){siftDown(0);}}// 获取堆顶元素T peek() const{if (heap.empty()){throw out_of_range("Heap is empty");}return heap[0];}// 获取并删除顶元素T pop(){T value = peek();remove();return value;}// 判断堆是否为空bool isEmpty() const{return heap.empty();}// 输出堆中的元素void print() const{for (const auto &elem : heap){cout << elem << " ";}cout << endl;}
};template <class T>
void BinaryHeapSort(vector<T> &data)
{BinaryHeap<T> heap;auto dataSize = data.size();for (auto i = 0; i < dataSize; i++)heap.insert(data[i]);for (auto i = 0; i < dataSize; i++)data[i] = heap.pop();
}
完整的项目代码
Python 代码
import mathclass Person:def __init__(self, name, age, score):self.name = nameself.age = ageself.score = scoredef __lt__(self, other):return self.score < other.scoredef __le__(self, other):return self.score <= other.scoredef __eq__(self, other):return self.score == other.score and self.age == other.age and self.name == other.namedef __ne__(self, other):return not self.__eq__(other)def __gt__(self, other):return self.score > other.scoredef __ge__(self, other):return self.score >= other.scoredef get_name(self):return self.namedef get_age(self):return self.agedef get_score(self):return self.scoredef heapify(arr, n, i):largest = ileft = 2 * i + 1right = 2 * i + 2if left < n and arr[i] < arr[left]:largest = leftif right < n and arr[largest] < arr[right]:largest = rightif largest != i:arr[i], arr[largest] = arr[largest], arr[i]heapify(arr, n, largest)def heapsort(arr):n = len(arr)for i in range(n//2 - 1, -1, -1):heapify(arr, n, i)for i in range(n-1, 0, -1):arr[i], arr[0] = arr[0], arr[i]heapify(arr, i, 0)def test_heap_sort():data = [9, 8, 3, 7, 5, 6, 4, 1]heapsort(data)print(data)d_data = [9.9, 9.1, 3.3, 7.7, 5.5, 6.6, 4.4, 1.1]heapsort(d_data)print(d_data)c_data = ['a', 'c', 'b', 'd', 'e']heapsort(c_data)print(c_data)p_data = [Person("Alice", 20, 90), Person("Bob", 18, 85), Person("Charlie", 22, 95)]heapsort(p_data)for person in p_data:print(person.get_name(), person.get_age(), person.get_score())class MaxHeap:def __init__(self):self.heap = []def parent(self, i):return (i - 1) // 2def left_child(self, i):return 2 * i + 1def right_child(self, i):return 2 * i + 2def has_left_child(self, i):return self.left_child(i) < len(self.heap)def has_right_child(self, i):return self.right_child(i) < len(self.heap)def swap(self, i, j):self.heap[i], self.heap[j] = self.heap[j], self.heap[i]def heapify_up(self, i):while i > 0 and self.heap[self.parent(i)] < self.heap[i]:self.swap(i, self.parent(i))i = self.parent(i)def heapify_down(self, i):largest = iif self.has_left_child(i) and self.heap[self.left_child(i)] > self.heap[largest]:largest = self.left_child(i)if self.has_right_child(i) and self.heap[self.right_child(i)] > self.heap[largest]:largest = self.right_child(i)if largest != i:self.swap(i, largest)self.heapify_down(largest)def insert(self, key):self.heap.append(key)self.heapify_up(len(self.heap) - 1)def extract_max(self):if len(self.heap) == 0:return Nonemax_value = self.heap[0]self.heap[0] = self.heap[-1]self.heap.pop()self.heapify_down(0)return max_valuedef build_heap(self, arr):self.heap = arr.copy()for i in range(len(self.heap) // 2, -1, -1):self.heapify_down(i)def is_empty(self):return len(self.heap) == 0def get_max(self):if self.is_empty():return Nonereturn self.heap[0]def __str__(self):return str(self.heap)def max_heap_sort(arr):max_heap = MaxHeap()max_heap.build_heap(arr)sorted_arr = []while not max_heap.is_empty():sorted_arr.append(max_heap.extract_max())return sorted_arr[::-1] # Reverse to get ascending orderclass FibonacciHeap:# internal node classclass Node:def __init__(self, key, value):self.key = keyself.value = valueself.parent = self.child = self.left = self.right = Noneself.degree = 0self.mark = False# function to iterate through a doubly linked listdef iterate(self, head):node = stop = headflag = Falsewhile True:if node == stop and flag is True:breakelif node == stop:flag = Trueyield nodenode = node.right# pointer to the head and minimum node in the root listroot_list, min_node = None, None# maintain total node count in full fibonacci heaptotal_nodes = 0# return min node in O(1) timedef find_min(self):return self.min_node# extract (delete) the min node from the heap in O(log n) time# amortized cost analysis can be found here (http://bit.ly/1ow1Clm)def extract_min(self):z = self.min_nodeif z is not None:if z.child is not None:# attach child nodes to root listchildren = [x for x in self.iterate(z.child)]for i in range(0, len(children)):self.merge_with_root_list(children[i])children[i].parent = Noneself.remove_from_root_list(z)# set new min node in heapif z == z.right:self.min_node = self.root_list = Noneelse:self.min_node = z.rightself.consolidate()self.total_nodes -= 1return z# insert new node into the unordered root list in O(1) time# returns the node so that it can be used for decrease_key laterdef insert(self, key, value=None):n = self.Node(key, value)n.left = n.right = nself.merge_with_root_list(n)if self.min_node is None or n.key < self.min_node.key:self.min_node = nself.total_nodes += 1return n# modify the key of some node in the heap in O(1) timedef decrease_key(self, x, k):if k > x.key:return Nonex.key = ky = x.parentif y is not None and x.key < y.key:self.cut(x, y)self.cascading_cut(y)if x.key < self.min_node.key:self.min_node = x# merge two fibonacci heaps in O(1) time by concatenating the root lists# the root of the new root list becomes equal to the first list and the second# list is simply appended to the end (then the proper min node is determined)def merge(self, h2):H = FibonacciHeap()H.root_list, H.min_node = self.root_list, self.min_node# fix pointers when merging the two heapslast = h2.root_list.lefth2.root_list.left = H.root_list.leftH.root_list.left.right = h2.root_listH.root_list.left = lastH.root_list.left.right = H.root_list# update min node if neededif h2.min_node.key < H.min_node.key:H.min_node = h2.min_node# update total nodesH.total_nodes = self.total_nodes + h2.total_nodesreturn H# if a child node becomes smaller than its parent node we# cut this child node off and bring it up to the root listdef cut(self, x, y):self.remove_from_child_list(y, x)y.degree -= 1self.merge_with_root_list(x)x.parent = Nonex.mark = False# cascading cut of parent node to obtain good time boundsdef cascading_cut(self, y):z = y.parentif z is not None:if y.mark is False:y.mark = Trueelse:self.cut(y, z)self.cascading_cut(z)# combine root nodes of equal degree to consolidate the heap# by creating a list of unordered binomial treesdef consolidate(self):A = [None] * int(math.log(self.total_nodes) * 2)nodes = [w for w in self.iterate(self.root_list)]for w in range(0, len(nodes)):x = nodes[w]d = x.degreewhile A[d] != None:y = A[d]if x.key > y.key:temp = xx, y = y, tempself.heap_link(y, x)A[d] = Noned += 1A[d] = x# find new min node - no need to reconstruct new root list below# because root list was iteratively changing as we were moving# nodes around in the above loopfor i in range(0, len(A)):if A[i] is not None:if A[i].key < self.min_node.key:self.min_node = A[i]# actual linking of one node to another in the root list# while also updating the child linked listdef heap_link(self, y, x):self.remove_from_root_list(y)y.left = y.right = yself.merge_with_child_list(x, y)x.degree += 1y.parent = xy.mark = False# merge a node with the doubly linked root listdef merge_with_root_list(self, node):if self.root_list is None:self.root_list = nodeelse:node.right = self.root_list.rightnode.left = self.root_listself.root_list.right.left = nodeself.root_list.right = node# merge a node with the doubly linked child list of a root nodedef merge_with_child_list(self, parent, node):if parent.child is None:parent.child = nodeelse:node.right = parent.child.rightnode.left = parent.childparent.child.right.left = nodeparent.child.right = node# remove a node from the doubly linked root listdef remove_from_root_list(self, node):if node == self.root_list:self.root_list = node.rightnode.left.right = node.rightnode.right.left = node.left# remove a node from the doubly linked child listdef remove_from_child_list(self, parent, node):if parent.child == parent.child.right:parent.child = Noneelif parent.child == node:parent.child = node.rightnode.right.parent = parentnode.left.right = node.rightnode.right.left = node.leftdef fibonacci_heap_sort(arr):heap = FibonacciHeap()for key in arr:heap.insert(key)sorted_arr = []while heap.total_nodes > 0:sorted_arr.append(heap.extract_min().key)return sorted_arrdef test_max_heap_sort():data = [9, 8, 3, 7, 5, 6, 4, 1]max_heap_sort(data)print(data)d_data = [9.9, 9.1, 3.3, 7.7, 5.5, 6.6, 4.4, 1.1]max_heap_sort(d_data)print(d_data)c_data = ['a', 'c', 'b', 'd', 'e']max_heap_sort(c_data)print(c_data)p_data = [Person("Alice", 20, 90), Person("Bob", 18, 85), Person("Charlie", 22, 95)]max_heap_sort(p_data)for person in p_data:print(person.get_name(), person.get_age(), person.get_score())def test_fibonacci_heap_sort():data = [9, 8, 3, 7, 5, 6, 4, 1]fibonacci_heap_sort(data)print(data)d_data = [9.9, 9.1, 3.3, 7.7, 5.5, 6.6, 4.4, 1.1]fibonacci_heap_sort(d_data)print(d_data)c_data = ['a', 'c', 'b', 'd', 'e']fibonacci_heap_sort(c_data)print(c_data)p_data = [Person("Alice", 20, 90), Person("Bob", 18, 85), Person("Charlie", 22, 95)]fibonacci_heap_sort(p_data)for person in p_data:print(person.get_name(), person.get_age(), person.get_score())if __name__ == "__main__":test_heap_sort()test_max_heap_sort()test_fibonacci_heap_sort()
C++ 代码
#include <iostream>
#include <array>
#include <algorithm>
#include <vector>
#include <string>
#include <cmath>
#include <list>
#include <iterator>using namespace std;class Person
{
public:Person() = default;~Person() = default;Person(string name, int age, int score){this->name = name;this->age = age;this->socre = score;}// Override the operator> for other function to use.bool operator>(const Person &other) const{// Compare the socre of two Person objects.return this->socre > other.socre;}// Override the operator< for other function to use.bool operator<(const Person &other) const{// Compare the socre of two Person objects.return this->socre < other.socre;}// Override the operator== for other function to use.bool operator==(const Person &other) const{// Compare the socre, age and name of two Person objects.return this->socre == other.socre &&this->age == other.age &&this->name == other.name;}// Override the operator!= for other function to use.bool operator!=(const Person &other) const{// Compare the socre, age and name of two Person objects.return this->socre != other.socre ||this->age != other.age ||this->name != other.name;}// Override the operator<= for other fnction to use.bool operator<=(const Person &other) const{// Compare the socre, age and name of two Person objects.return this->socre <= other.socre &&this->age <= other.age &&this->name <= other.name;}// Override the operator>= for other function to use.bool operator>=(const Person &other) const{// Compare the socre, age and name of two Person objects.return this->socre >= other.socre &&this->age >= other.age &&this->name >= other.name;}// Now there are some get parameters function for this calss:const string &getName() const { return this->name; }int getAge() const { return this->age; }int getScore() const { return this->socre; }private:string name;int age;int socre;
};template <typename RandomAccessIterator>
void siftDown(RandomAccessIterator start, RandomAccessIterator end, RandomAccessIterator root)
{auto child = root;advance(child, distance(start, root) + 1);if (child < end){auto sibling = child;++sibling;if (sibling<end && * sibling> * child){child = sibling;}if (*child > *root){iter_swap(root, child);siftDown(start, end, child);}}
}template <typename RandomAccessIterator>
void makeHeap(RandomAccessIterator start, RandomAccessIterator end)
{if (start != end){auto length = distance(start, end);auto parent = start;advance(parent, (length - 2) / 2);while (true){siftDown(start, end, parent);if (parent == start)break;--parent;}}
}template <typename RandomAccessIterator>
void heapSort(RandomAccessIterator start, RandomAccessIterator end)
{makeHeap<RandomAccessIterator>(start, end);while (start != end){--end;iter_swap(start, end);siftDown(start, end, start);}
}void heapSortTestCase()
{vector<int> data = {9, 8, 3, 7, 5, 6, 4, 1};heapSort<vector<int>::iterator>(data.begin(), data.end());for (int i : data){cout << i << " ";}cout << endl;vector<double> dData = {9.9, 9.1, 3.3, 7.7, 5.5, 6.6, 4.4, 1.1};heapSort<vector<double>::iterator>(dData.begin(), dData.end());for (double i : dData){cout << i << " ";}cout << endl;vector<char> cData = {'a', 'c', 'b', 'd', 'e'};heapSort<vector<char>::iterator>(cData.begin(), cData.end());for (char i : cData){cout << i << " ";}cout << endl;vector<Person> pData = {Person("Alice", 20, 90), Person("Bob", 18, 85), Person("Charlie", 22, 95)};heapSort<vector<Person>::iterator>(pData.begin(), pData.end());for (Person i : pData){cout << i.getName() << " " << i.getAge() << " " << i.getScore() << endl;}cout << endl;
}template <typename T>
void maxHeapify(vector<T> &arr, int i, int n)
{int left = 2 * i + 1;int right = 2 * i + 2;int largest = i;if (left < n && arr[left] > arr[largest]){largest = left;}if (right < n && arr[right] > arr[largest]){largest = right;}if (largest != i){swap(arr[i], arr[largest]);maxHeapify(arr, largest, n);}
}template <typename T>
void binaryHeapSort(vector<T> &arr)
{int n = arr.size();// Build max heapfor (int i = n / 2 - 1; i >= 0; i--){maxHeapify(arr, i, n);}// Extract elements from heapfor (int i = n - 1; i >= 0; i--){swap(arr[0], arr[i]);maxHeapify(arr, 0, i);}
}void binaryHeapSortTestCase()
{vector<int> data = {9, 8, 3, 7, 5, 6, 4, 1};binaryHeapSort<int>(data);for (int i : data){cout << i << " ";}cout << endl;vector<double> dData = {9.9, 9.1, 3.3, 7.7, 5.5, 6.6, 4.4, 1.1};binaryHeapSort<double>(dData);for (double i : dData){cout << i << " ";}cout << endl;vector<char> cData = {'a', 'c', 'b', 'd', 'e'};binaryHeapSort<char>(cData);for (char i : cData){cout << i << " ";}cout << endl;vector<Person> pData = {Person("Alice", 20, 90), Person("Bob", 18, 85), Person("Charlie", 22, 95)};binaryHeapSort<Person>(pData);for (Person i : pData){cout << i.getName() << " " << i.getAge() << " " << i.getScore() << endl;}cout << endl;
}template <typename T>
class BinaryHeap
{
private:vector<T> heap;// 用于将新插入的元素上浮到正确位置void siftUp(int index){while (index > 0 && heap[(index - 1) / 2] < heap[index]){swap(heap[index], heap[(index - 1) / 2]);index = (index - 1) / 2;}}// 用于将堆顶元素下沉到正确位置void siftDown(int index){int left = 2 * index + 1;int right = 2 * index + 2;int largest = index;if (left < heap.size() && heap[left] > heap[largest]){largest = left;}if (right < heap.size() && heap[right] > heap[largest]){largest = right;}if (largest != index){swap(heap[index], heap[largest]);siftDown(largest);}}public:BinaryHeap() {}// 插入元素void insert(T value){heap.push_back(value);siftUp(heap.size() - 1);}// 删除堆顶元素void remove(){if (heap.empty()){return;}heap[0] = heap.back();heap.pop_back();if (!heap.empty()){siftDown(0);}}// 获取堆顶元素T peek() const{if (heap.empty()){throw out_of_range("Heap is empty");}return heap[0];}// 获取并删除顶元素T pop(){T value = peek();remove();return value;}// 判断堆是否为空bool isEmpty() const{return heap.empty();}// 输出堆中的元素void print() const{for (const auto &elem : heap){cout << elem << " ";}cout << endl;}
};template <class T>
void BinaryHeapSort(vector<T> &data)
{BinaryHeap<T> heap;auto dataSize = data.size();for (auto i = 0; i < dataSize; i++)heap.insert(data[i]);for (auto i = 0; i < dataSize; i++)data[i] = heap.pop();
}void BinaryHeapUnitTest()
{BinaryHeap<int> maxHeap;maxHeap.insert(10);maxHeap.insert(20);maxHeap.insert(15);maxHeap.insert(17);maxHeap.insert(25);maxHeap.print(); // 应该输出 25 20 15 17 10cout << "Peek: " << maxHeap.peek() << endl; // 应该输出 25maxHeap.remove();maxHeap.print(); // 应该输出 20 17 15 10
}void BinaryHeapSortTestCase()
{vector<int> data = {9, 8, 3, 7, 5, 6, 4, 1};BinaryHeapSort<int>(data);for (int i : data){cout << i << " ";}cout << endl;vector<double> dData = {9.9, 9.1, 3.3, 7.7, 5.5, 6.6, 4.4, 1.1};BinaryHeapSort<double>(dData);for (double i : dData){cout << i << " ";}cout << endl;vector<char> cData = {'a', 'c', 'b', 'd', 'e'};BinaryHeapSort<char>(cData);for (char i : cData){cout << i << " ";}cout << endl;vector<Person> pData = {Person("Alice", 20, 90), Person("Bob", 18, 85), Person("Charlie", 22, 95)};BinaryHeapSort<Person>(pData);for (Person i : pData){cout << i.getName() << " " << i.getAge() << " " << i.getScore() << endl;}cout << endl;
}template <class V>
class FibonacciHeap;template <class V>
struct node
{
private:node<V> *prev;node<V> *next;node<V> *child;node<V> *parent;V value;int degree;bool marked;public:friend class FibonacciHeap<V>;node<V> *getPrev() { return prev; }node<V> *getNext() { return next; }node<V> *getChild() { return child; }node<V> *getParent() { return parent; }V getValue() { return value; }bool isMarked() { return marked; }bool hasChildren() { return child; }bool hasParent() { return parent; }
};template <class V>
class FibonacciHeap
{
protected:node<V> *heap;public:FibonacciHeap(){heap = _empty();}virtual ~FibonacciHeap(){if (heap){_deleteAll(heap);}}node<V> *insert(V value){node<V> *ret = _singleton(value);heap = _merge(heap, ret);return ret;}void merge(FibonacciHeap &other){heap = _merge(heap, other.heap);other.heap = _empty();}bool isEmpty(){return heap == nullptr;}V getMinimum(){return heap->value;}V removeMinimum(){node<V> *old = heap;heap = _removeMinimum(heap);V ret = old->value;delete old;return ret;}void decreaseKey(node<V> *n, V value){heap = _decreaseKey(heap, n, value);}node<V> *find(V value){return _find(heap, value);}private:node<V> *_empty(){return nullptr;}node<V> *_singleton(V value){node<V> *n = new node<V>;n->value = value;n->prev = n->next = n;n->degree = 0;n->marked = false;n->child = nullptr;n->parent = nullptr;return n;}node<V> *_merge(node<V> *a, node<V> *b){if (a == nullptr)return b;if (b == nullptr)return a;if (a->value > b->value){node<V> *temp = a;a = b;b = temp;}node<V> *an = a->next;node<V> *bp = b->prev;a->next = b;b->prev = a;an->prev = bp;bp->next = an;return a;}void _deleteAll(node<V> *n){if (n != nullptr){node<V> *c = n;do{node<V> *d = c;c = c->next;_deleteAll(d->child);delete d;} while (c != n);}}void _addChild(node<V> *parent, node<V> *child){child->prev = child->next = child;child->parent = parent;parent->degree++;parent->child = _merge(parent->child, child);}void _unMarkAndUnParentAll(node<V> *n){if (n == nullptr)return;node<V> *c = n;do{c->marked = false;c->parent = nullptr;c = c->next;} while (c != n);}node<V> *_removeMinimum(node<V> *n){_unMarkAndUnParentAll(n->child);if (n->next == n){n = n->child;}else{n->next->prev = n->prev;n->prev->next = n->next;n = _merge(n->next, n->child);}if (n == nullptr)return n;node<V> *trees[64] = {nullptr};while (true){if (trees[n->degree] != nullptr){node<V> *t = trees[n->degree];if (t == n)break;trees[n->degree] = nullptr;if (n->value < t->value){t->prev->next = t->next;t->next->prev = t->prev;_addChild(n, t);}else{t->prev->next = t->next;t->next->prev = t->prev;if (n->next == n){t->next = t->prev = t;_addChild(t, n);n = t;}else{n->prev->next = t;n->next->prev = t;t->next = n->next;t->prev = n->prev;_addChild(t, n);n = t;}}continue;}else{trees[n->degree] = n;}n = n->next;}node<V> *min = n;node<V> *start = n;do{if (n->value < min->value)min = n;n = n->next;} while (n != start);return min;}node<V> *_cut(node<V> *heap, node<V> *n){if (n->next == n){n->parent->child = nullptr;}else{n->next->prev = n->prev;n->prev->next = n->next;n->parent->child = n->next;}n->next = n->prev = n;n->marked = false;return _merge(heap, n);}node<V> *_decreaseKey(node<V> *heap, node<V> *n, V value){if (n->value < value)return heap;n->value = value;if (n->parent){if (n->value < n->parent->value){heap = _cut(heap, n);node<V> *parent = n->parent;n->parent = nullptr;while (parent != nullptr && parent->marked){heap = _cut(heap, parent);n = parent;parent = n->parent;n->parent = nullptr;}if (parent != nullptr && parent->parent != nullptr)parent->marked = true;}}else{if (n->value < heap->value){heap = n;}}return heap;}node<V> *_find(node<V> *heap, V value){node<V> *n = heap;if (n == nullptr)return nullptr;do{if (n->value == value)return n;node<V> *ret = _find(n->child, value);if (ret)return ret;n = n->next;} while (n != heap);return nullptr;}
};class DotFibonacciHeap : public FibonacciHeap<int>
{
public:void dump(){printf("digraph G {\n");if (heap == nullptr){printf("empty;\n}\n");return;}printf("minimum -> \"%p\" [constraint=false];\n", heap);node<int> *c = heap;do{_dumpChildren(c);c = c->getNext();} while (c != heap);printf("}\n");}private:void _dumpChildren(node<int> *n){printf("\"%p\" -> \"%p\" [constraint=false,arrowhead=lnormal];\n", n, n->getNext());printf("\"%p\" -> \"%p\" [constraint=false,arrowhead=ornormal];\n", n, n->getPrev());if (n->isMarked())printf("\"%p\" [style=filled,fillcolor=grey];\n", n);if (n->hasParent()){printf("\"%p\" -> \"%p\" [constraint=false,arrowhead=onormal];\n", n, n->getParent());}printf("\"%p\" [label=%d];\n", n, n->getValue());if (n->hasChildren()){node<int> *c = n->getChild();do{printf("\"%p\" -> \"%p\";\n", n, c);_dumpChildren(c);c = c->getNext();} while (c != n->getChild());}}
};void DotFibonacciHeapUnitTest()
{DotFibonacciHeap h;h.insert(2);h.insert(3);h.insert(1);h.insert(4);h.removeMinimum();h.removeMinimum();h.insert(5);h.insert(7);h.removeMinimum();h.insert(2);node<int> *nine = h.insert(90);h.removeMinimum();h.removeMinimum();h.removeMinimum();for (int i = 0; i < 20; i += 2)h.insert(30 - i);for (int i = 0; i < 4; i++)h.removeMinimum();for (int i = 0; i < 20; i += 2)h.insert(30 - i);h.insert(23);for (int i = 0; i < 7; i++)h.removeMinimum();h.decreaseKey(nine, 1);h.decreaseKey(h.find(28), 2);h.decreaseKey(h.find(23), 3);h.dump();
}template <class T>
void FibonacciHeapSort(vector<T> &data)
{FibonacciHeap<T> heap;auto dataSize = data.size();for (auto i = 0; i < dataSize; i++)heap.insert(data[i]);for (auto i = 0; i < dataSize; i++)data[i] = heap.removeMinimum();
}void FibonacciHeapSortTestCase()
{vector<int> data = {9, 8, 3, 7, 5, 6, 4, 1};FibonacciHeapSort<int>(data);for (int i : data){cout << i << " ";}cout << endl;vector<double> dData = {9.9, 9.1, 3.3, 7.7, 5.5, 6.6, 4.4, 1.1};FibonacciHeapSort<double>(dData);for (double i : dData){cout << i << " ";}cout << endl;vector<char> cData = {'a', 'c', 'b', 'd', 'e'};FibonacciHeapSort<char>(cData);for (char i : cData){cout << i << " ";}cout << endl;vector<Person> pData = {Person("Alice", 20, 90), Person("Bob", 18, 85), Person("Charlie", 22, 95)};FibonacciHeapSort<Person>(pData);for (Person i : pData){cout << i.getName() << " " << i.getAge() << " " << i.getScore() << endl;}cout << endl;
}int main()
{cout << "Heap Sort Case:" << endl;heapSortTestCase();cout << "Binary Heap Sort Case Without DataStructure:" << endl;binaryHeapSortTestCase();cout << "Binary Heap Sort Case With DataStructure:" << endl;BinaryHeapUnitTest();BinaryHeapSortTestCase();cout << "Fibonacci Heap Sort Case:" << endl;DotFibonacciHeapUnitTest();FibonacciHeapSortTestCase();return 0;
}
个人格言
追寻与内心共鸣的生活,未来会逐渐揭晓答案。
Pursue the life that resonates with your heart, and the future will gradually reveal the answer.

相关文章:

[算法沉淀记录] 排序算法 —— 堆排序
排序算法 —— 堆排序 算法基础介绍 堆排序(Heap Sort)是一种基于比较的排序算法,它利用堆这种数据结构来实现排序。堆是一种特殊的完全二叉树,其中每个节点的值都必须大于或等于(最大堆)或小于或等于&am…...

C++ //练习 9.33 在本节最后一个例子中,如果不将insert的结果赋予begin,将会发生什么?编写程序,去掉此赋值语句,验证你的答案。
C Primer(第5版) 练习 9.33 练习 9.33 在本节最后一个例子中,如果不将insert的结果赋予begin,将会发生什么?编写程序,去掉此赋值语句,验证你的答案。 环境:Linux Ubuntu࿰…...
[corCTF 2022] CoRJail: From Null Byte Overflow To Docker Escape
前言 题目来源:竞赛官网 – 建议这里下载,文件系统/带符号的 vmlinux 给了 参考 [corCTF 2022] CoRJail: From Null Byte Overflow To Docker Escape Exploiting poll_list Objects In The Linux Kernel – 原作者文章,poll_list 利用方式…...
thinkphp6定时任务
这里主要是教没有用过定时任务没有头绪的朋友, 定时任务可以处理一些定时备份数据库等一系列操作, 具体根据自己的业务逻辑进行更改 直接上代码 首先, 是先在 tp 中的 command 方法中声明, 如果没有就自己新建一个, 代码如下 然后就是写你的业务逻辑 执行定时任务 方法写好了…...
)
支持国密ssl的curl编译和测试验证(上)
目录 1. 编译铜锁ssl库2. 编译nghttp2库3. 编译curl4. 验证4.1 查看版本信息4.2 验证国密ssl握手功能4.3 验证http2协议功能 以下以ubuntu 22.04环境为例进行编译 本次编译采用铜锁sslnghttp2curl,使得编译出来的curl可以支持国密ssl,并且可以支持http2…...

包装类详解
概述 Java提供了两个类型系统,基本类型与引用类型,使用基本类型在于效率,然而很多情况,会创建对象使用,因为对象可以做更多的功能,如果想要我们的基本类型像对象一样操作,就可以使用基本类型对…...

vue3与vue2的区别
Vue 3和Vue 2在以下几个方面有一些区别: 性能提升:Vue 3对渲染性能和内存占用进行了优化,使用了Proxy代理对象,比Vue 2的Object.defineProperty更高效。此外,Vue 3还引入了静态树提升(Static Tree Hoisting…...
SSL OV证书和DV、EV证书的区别
在网站搭建的过程中和小程序开发过程中,很难免会有需要用到SSL证书的地方,但是目前数字证书种类繁多,该选择什么类型的证书成为了一个令人纠结的问题。 目前在市场上较为常见的证书分为三种:DV域名验证型证书;OV组织验…...
一款.NET下 WPF UI框架介绍
WPF开源的UI框架有很多,如HandyControl、MahApps.Metro、Xceed Extended WPF Toolkit™、Modern UI for WPF (MUI)、Layui-WPF、MaterialDesignInXamlToolkit、等等,今天小编带大家认识一款比较常用的kaiyuanUI---WPF UI,这款ui框架美观现代化,用起来也超级方便, 界面展示…...
东莞IBM服务器维修之IBM x3630 M4阵列恢复
记录东莞某抖音电商公司送修一台IBM SYSTEM X3630 M4文档服务器RAID6故障导致数据丢失的恢复案例 时间:2024年02月20日, 服务器品牌:IBM System x3630 M4,阵列卡用的是DELL PERC H730P 服务器用途和用户位置:某抖音电…...
Flask基础学习4
19-【实战】问答平台项目结构搭建_剪_哔哩哔哩_bilibili 参考如上大佬的视频教程,本博客仅当学习笔记,侵权请联系删除 问答发布的web前端页面实现 register.html {% extends base.html %}{% block head %}<link rel"stylesheet" href&q…...
mac安装zookeeper
下载地址: http://archive.apache.org/dist/zookeeper/ 注意:由于Zookeeper从3.5.5版本开始,带有bin名称的包才是我们想要的下载可以直接使用的里面有编译后的二进制的包,而之前的普通的tar.gz的包里面是只是源码的包无法直接使…...

IT资讯——全速推进“AI+鸿蒙”战略布局!
文章目录 每日一句正能量前言坚持长期研发投入全速推进“AI鸿蒙”战略 人才战略新章落地持续加码核心技术生态建设 后记 每日一句正能量 人总要咽下一些委屈,然后一字不提的擦干眼泪往前走,没有人能像白纸一样没有故事,成长的代价就是失去原来…...
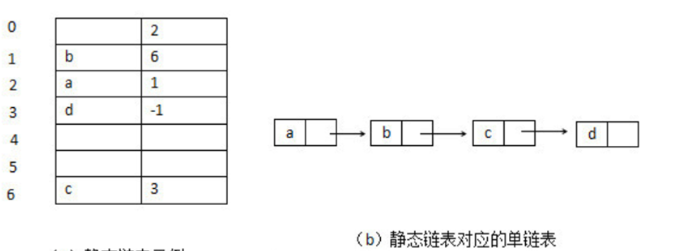
数据结构知识点总结-线性表(3)-双向链表定义、循环单链表、、循环双向链表、静态链表、顺序表与链表的比较
双向链表定义 单链表结点中只有一个指向其后继的指针,这使得单链表只能从头结点依次顺序地向后遍历。若要访问某个结点的前驱结点(插入、删除操作时),只能从头开始遍历,访问后继结点的时间复杂度为 O(1) , …...

JAVA学习-控制执行流程.for
在Java中,for循环是一种常用的控制执行流程的循环语句。它允许我们重复执行一段代码,直到满足指定的循环条件。 一、for循环的基本语法如下: for (初始化语句; 循环条件; 循环后操作) {// 循环体,要执行的代码} 其中,…...
面试总结之JVM入门
文章目录 🐒个人主页🏅JavaEE系列专栏📖前言:🎀你为什么要学习JVM?🎀JVM的作用 🎀JVM的构成(5大类)🏨1.类加载系统🐕类什么时候会被加…...
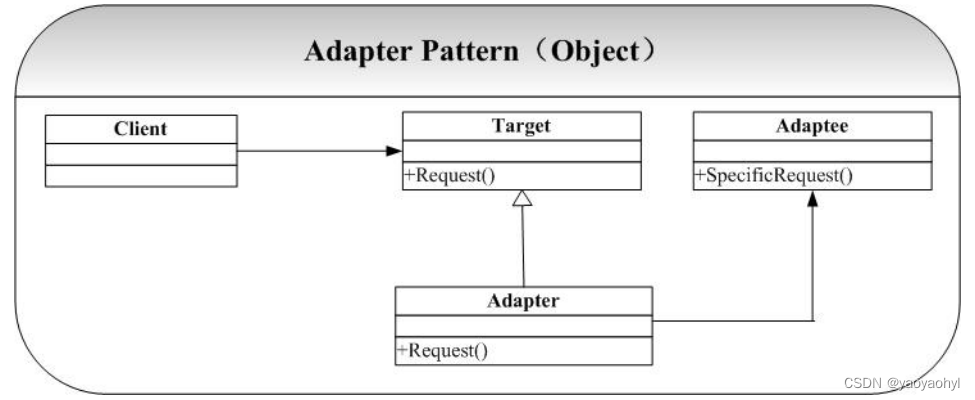
适配器模式(Adapter Pattern) C++
上一节:原型模式(Prototype Pattern) C 文章目录 0.理论1.组件2.类型3.什么时候使用 1.实践1.基础接口和类2.类适配器实现3.对象适配器实现 0.理论 适配器模式(Adapter Pattern)是一种结构型设计模式,它允…...

【程序员英语】【美语从头学】初级篇(入门)(笔记)Lesson 16 At the Shoe Store 在鞋店
《美语从头学初级入门篇》 注意:被 删除线 划掉的不一定不正确,只是不是标准答案。 文章目录 Lesson 16 At the Shoe Store 在鞋店对话A对话B笔记会话A会话B替换 Lesson 16 At the Shoe Store 在鞋店 对话A A: Do you have these shoes in size 8? B:…...

嵌入式系统在物联网中的应用与发展趋势
嵌入式系统在物联网中的应用与发展趋势 嵌入式系统在物联网中扮演着至关重要的角色,它们是连接物理世界和数字世界的桥梁,实现了物体之间的互联互通。以下是嵌入式系统在物联网中的应用与发展趋势的几个方面: 1. 应用领域 智能家居&#x…...
BTC网络 vs ETH网络
设计理念 BTC 网络 比特币是一种数字货币,旨在作为一种去中心化的、不受政府或金融机构控制的电子货币。其主要目标是实现安全的价值传输和储存,比特币的设计强调去中心化和抗审查。 ETH 网络 以太坊是一个智能合约平台,旨在支持分散的应…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
