xmu 离散数学 卢杨班作业详解【8-12章】
文章目录
- 第八章 树
- 2
- 3
- 4
- 5
- 6
- 8
- 10
- 第九章
- 4
- 6
- 8
- 11
- 第十章
- 2
- 4
- 5
- 6
- 7
- 第十一章
- 1
- 4
- 5
- 7
- 11
- 16
- 第十二章
- 1
- 3
- 13
- 17
第八章 树
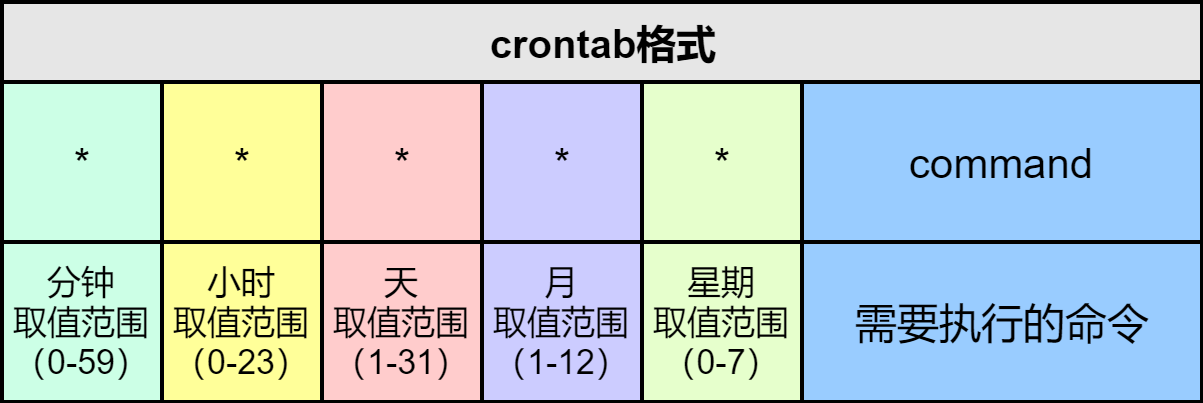
2
(2)
设有k片树叶
2∗m=2∗4+3∗3+k2*m=2*4+3*3+k2∗m=2∗4+3∗3+k
n=2+3+kn=2+3+kn=2+3+k
m=n−1m=n-1m=n−1
联立解得k=9
T中有9片树叶
3

有三颗非同构的生成树
4
(1)
c --abc
e–abed
f–dgf
h–abhgd
(2)
T的树枝a,b,d,g,对应的基本割集系统为{a,c,e,h},{b,c,e,h},{d,e,h,f},{g,f,h}
5

6
(1)
((a+b∗c)∗d−e)/(f+g)+h∗i∗j((a+b*c)*d-e)/(f+g)+h*i*j((a+b∗c)∗d−e)/(f+g)+h∗i∗j
(2)
+/−∗+a∗bcde+fg∗∗hij+/-*+a*bcde+fg**hij+/−∗+a∗bcde+fg∗∗hij
(3)
abc∗+d∗e−fg+/hi∗j∗+abc*+d*e-fg+/hi*j*+abc∗+d∗e−fg+/hi∗j∗+
8
简单图:不含环和平行边
不一定是树。未保证连通
10
在树中,仅有分支点和树叶点
故
i+t=ni+t=ni+t=n
又因边数m为i∗ri*ri∗r
m=n-1
i+t=i∗r+1↔t=i∗(r−1)+1i+t=i*r+1 \leftrightarrow t=i*(r-1)+1i+t=i∗r+1↔t=i∗(r−1)+1
第九章
4
(3)偶数个顶点,奇数条边

(4)奇数个顶点,偶数条边

6
(2)是欧拉图,而不是哈密顿图

(3)是哈密顿图,而不是欧拉图

8

11
A-D-C-B-A
第十章
2
deg(R1)=5
deg(R2)=3
deg(R0)=12
4

通过画图可知,无论怎样,两图都会有相交的边,故为非平面图
5

6
(1)点色数χ\chiχ

将原图标号,可得,1234为4阶圈,偶数阶,点色数为2。5与1,3不可同色,又1,3不同色,故色数+1。同理可知6,7。5,6,7不相邻,故可使用同一颜色着色。得出结论点色数χ\chiχ为3
(2)面色数χ′\chi'χ′

2与1,3相邻,与4不相邻,1,3不相邻。故1234的面色数为2。5与2相邻,与1,3不相邻。故可用于1,3同色的着色。6同理。故面色数为χ′\chi'χ′为2
7
实际为着色问题。要求有同时选修的课程,考试时间不同,也就是着色颜色不同。

1 2 3 5为4阶圈,偶数阶,点色数为2。4与1,3相邻,4与1,3颜色不同。1,3相邻,颜色不同。故点色数为3。至少需要3个
第十一章
1
(1)A53=5×4×3=60A_5^3=5\times4\times3=60A53=5×4×3=60 种
(2)53=1255^3=12553=125 种
4
(1)
A1010A44×A33×A33=10!4!×3!×3!=4200{A_{10}^{10}\over{A_4^4\times A_3^3\times A_3^3}}={10!\over{4!\times3!\times3!}}=4200A44×A33×A33A1010=4!×3!×3!10!=4200 种
(2)
A77A33×A33=140{A_7^7\over{A_3^3\times A_3^3}}=140A33×A33A77=140 种
5
(1)
要求a之间不相邻,则将a之间的4个空 有顺序的插入{b c d e}即可。
A44=24A_4^4=24A44=24 种
(2)
先将bcde排序,再往其中插入a。要求互不相邻,则内部的3个空一定得有a。多出的一个a插在bcde内部+外部共5个空其中一个即可
A44×C51=120A_4^4\times C_5^1=120A44×C51=120 种
7
盒子中容纳球可能的情况有:
(1)
2 2 0
$ {C_4^2\times C_2^2\times C_0^0\over A_2^2\times A_2^2 }\times A_3^3=9$ 种
(2)
2 1 1
$ {C_4^2\times C_2^1\times C_1^1\over {A_2^2}}\times A_3^3 =36$ 种
11
用全部情况减去5,6相邻
A97−A87A22=161280A_9^7-{A_8^7\over A_2^2}=161280A97−A22A87=161280 种
16
(1)不同的二元关系:
3元集的运算表共有9个位置,每个位置有3个值可选。故有39=196833^9=1968339=19683 个不同的二元关系
(2)自反的关系
自反的关系,对角线的三个位置为<x,x>=x<x,x>=x<x,x>=x 固定。其余6个位置,每个位置有3个值可选。故有36=7293^6=72936=729 个自反的二元关系
(3)对称的关系
转为三角矩阵,只需确定对角线+右上角即可。故有36=7293^6=72936=729 个对称的二元关系
(4)自反且对称的关系
转为三角矩阵,对角线的三个位置为<x,x>=x<x,x>=x<x,x>=x 固定,只需确定右上角即可。故有33=273^3=2733=27 个自反且对称的二元关系
(5)反对称的关系
39−36=189543^9-3^6=1895439−36=18954 个反对称的二元关系
第十二章
1
(1)
该递推方程的特征方程是 x2−2x−2=0x^2-2x-2=0x2−2x−2=0 ,特征根是
x1=1−3,x2=1+3x_1=1-\sqrt3,x_2=1+\sqrt3x1=1−3,x2=1+3
通解为c1(1−3)n+c2(1+3)nc_1(1-\sqrt3)^n+c_2(1+\sqrt3)^nc1(1−3)n+c2(1+3)n
带入初值a0=1,a1=3a_0=1,a_1=3a0=1,a1=3
c1+c2=1c1(1−3)+c2(1+3)=3解得c1=−33,c2=33c_1+c_2=1\\ c_1(1-\sqrt3)+c_2(1+\sqrt3)=3\\ 解得c_1=-{\sqrt3\over 3},c_2={\sqrt3\over 3} c1+c2=1c1(1−3)+c2(1+3)=3解得c1=−33,c2=33
(3)
该方程的常系数线性齐次递推方程的特征方程是 x2−3x+2=0x^2-3x+2=0x2−3x+2=0 ,特征根是
x1=1,x2=2x_1=1,x_2=2x1=1,x2=2
齐次方程通解为c11n+c22nc_11^n+c_22^nc11n+c22n
设特解形式为
H∗(n)=q1nH*(n)=q_1nH∗(n)=q1n ,其中q1q_1q1 为待定系数,带入原式
q1n−3q1(n−1)+2q1(n−2)=13q1−4q1=1解得q1=−1q_1n-3q_1(n-1)+2q_1(n-2)=1\\ 3q_1-4q_1=1\\ 解得q_1=-1 q1n−3q1(n−1)+2q1(n−2)=13q1−4q1=1解得q1=−1
因此通解为an=c1+c22n−na_n=c_1+c_22^n-nan=c1+c22n−n
带入初值得an=3×2n−n+1a_n=3\times2^n-n+1an=3×2n−n+1
3
an=7an−1+8n−1−an−1a_n=7a_{n-1}+8^{n-1}-a_{n-1}an=7an−1+8n−1−an−1,a1=7a_1=7a1=7
齐次特征方程为
x2−6x=0x^2-6x=0x2−6x=0
特征根为0或6,0舍去
齐次通解为an=c1×6na_n=c_1\times6^nan=c1×6n
设特解形式为
H∗(n)=q18nH*(n)=q_18^nH∗(n)=q18n ,其中q1q_1q1 为待定系数,带入原式
q18n=6×8n−1+8n−1q_18^n=6\times8^{n-1}+8^{n-1}q18n=6×8n−1+8n−1,q1=78q_1={7\over 8}q1=87
因此通解为an=c16n+78n−1a_n=c_16^n+78^{n-1}an=c16n+78n−1
带入初值,通解为an=6n+8n2a_n={6^n+8^n\over 2}an=26n+8n
13
原题可理解为x1+x2+x3+x4=6且xi不超过3的非负整数解的个数。
G(y) = (1+y+y2^22+y3^33)4^44 = (1+2y+3y2^22+4y3^33+3y4^44+2y5^55+y6^66)2^22 = 1+…+44y6^66+…
N = 44.
17
指数生成函数为
Ge(x) = (1+x+x22!{x^2} \over {2!}2!x2+x33!{x^3} \over {3!}3!x3)(1+x+x22!{x^2} \over {2!}2!x2)(1+x+x22!{x^2} \over {2!}2!x2+x33!{x^3} \over {3!}3!x3+x44!{x^4} \over {4!}4!x4+x55!{x^5} \over {5!}5!x5)
化简得x4x^4x4 的系数是71*x44!{x^4} \over {4!}4!x4 ,因此a4 = 71.
若为偶数,末位为2,对应的指数生成函数为
Ge(x) = (1+x+x22!{x^2} \over {2!}2!x2+x33!{x^3} \over {3!}3!x3)(1+x)(1+x+x22!{x^2} \over {2!}2!x2+x33!{x^3} \over {3!}3!x3+x44!{x^4} \over {4!}4!x4+x55!{x^5} \over {5!}5!x5)
化简得x3x^3x3的系数是20*x33!{x^3} \over {3!}3!x3 , 因此a3 = 20.
相关文章:

xmu 离散数学 卢杨班作业详解【8-12章】
文章目录第八章 树23456810第九章46811第十章24567第十一章14571116第十二章131317第八章 树 2 (2) 设有k片树叶 2∗m2∗43∗3k2*m2*43*3k2∗m2∗43∗3k n23kn23kn23k mn−1mn-1mn−1 联立解得k9 T中有9片树叶 3 有三颗非同构的生成树 4 (1) c --abc e–abed f–dgf…...

Linux入门篇-权限管理
简介 用户管理也是和权限相关的知识点。权限的作用 权限对于普通文件和目录文件作用是不一样的 。[kioskfoundation0 ~]$ ls -l total 264 -rw-rw-r--. 2 kiosk kiosk 31943 May 29 2019 ClassPrep.txt -rw-rw-r--. 2 kiosk kiosk 7605 Jun 14 2019 ClassRHAPrep.txt -rw-rw-r…...
Linux(基于 Centos7) 常用操作
1.Linux 简介Linux 是一种 免费使用、自由传播的类 Unix 操作系统Linux操作系统内核,由林纳斯托瓦兹在1991年10月5日首次发布...Linux 是一套开源操作系统,它有稳定、消耗资源小、安全性高等特点大多数人都是直接使用 Linux 发行版(就是将 Li…...

Math类详解与Random类、三种随机数生成方式(java)
文章目录📖前言:🎀认识Random类🎀三种随机数生成方式🎀Math类的用途🎀Math类的方法📖前言: 本篇博客主要以介绍Math类的常用方法及认识Random类,及三种随机数生成方式 …...

Mac编译QT程序出现Undefined symbols for architecture x86_64
在Mac编写日志服务类, Logging_d.h内容如下 #pragma once #include <QLoggingCategory> Q_DECLARE_LOGGING_CATEGORY(hovering) Q_DECLARE_LOGGING_CATEGORY(creation) Q_DECLARE_LOGGING_CATEGORY(mouseevents) Q_DECLARE_LOGGING_CATEGORY(state) Q_DECLARE_LOGGING_C…...
蓝桥杯-李白打酒加强版
蓝桥杯-李白打酒加强版1、问题描述2、解题思路3、代码实现1、问题描述 话说大诗人李白, 一生好饮。幸好他从不开车。 一天, 他提着酒显, 从家里出来, 酒显中有酒 2 斗。他边走边唱: 无事街上走,提显去打酒。 逢店加一倍, 遇花喝一斗。 这一路上, 他一共遇到店 N 次…...
 记录第一场ABC)
AtCoder Beginner Contest 292 (A - E) 记录第一场ABC
AtCoder Beginner Contest 292 A - E前言Q1 A - CAPS LOCKQ2 Yellow and Red CardQ3 Four VariablesQ4 D - Unicyclic ComponentsQ5 E - Transitivity前言 本来晚上在打Acwing周赛,最后一题Trie想不出来咋写,看群里有人说ABC要开始了,想着没…...
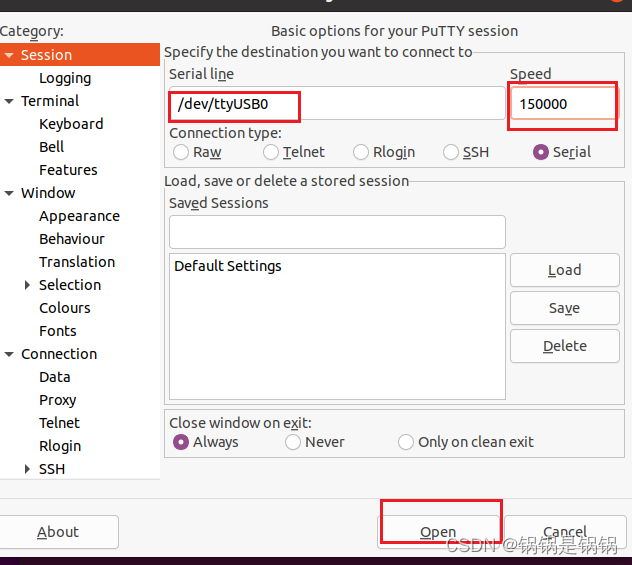
ubuntu安装使用putty
一、安装 安装虚拟机串口 sudo apt-get install putty sudo apt install -y setserial 二、使用 虚拟机连接串口 sudo setserial -g /dev/ttyS* 查看硬件对应串口 找到不是unknown的串口 sudo putty...

【CS144】Lab5与Lab6总结
Lab5与Lab6Lab汇总Lab5概述Lab6概述由于Lab5和Lab6相对比较简单(跟着文档一步一步写就行),于是放在一起做一个简单概述(主要是懒得写了…) Lab汇总 Lab5概述 lab5要求实现一个IP与Ethernet(以太网&#x…...

GDScript 导出变量 (Godot4.0)
概述 导出变量的功能在3.x版本中也是有的,但是4.0版本对其进行了语法上的改进。 导出变量在日常的游戏制作中提供节点的自定义参数化调节功能时非常有用,除此之外还用于自定义资源。 本文是(Bilibili巽星石)在4.0官方文档《GDScr…...
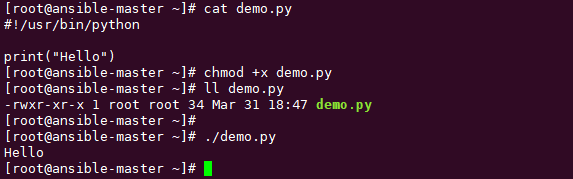
shell:#!/usr/bin/env python作用是什么
我们经常会在别人的脚本文件里看到第一行是下面这样 #!/usr/bin/python或者 #!/usr/bin/env python 那么他们有什么用呢? 要理解它,得把这一行语句拆成两部分。 第一部分是 #! 第二部分是 /usr/bin/python 或者 /usr/bin/env python 关于 #! 这个…...

计算机行业AIGC算力时代系列报告-ChatGPT芯片算力:研究框架
报告下载: 计算机行业AIGC算力时代系列报告-ChatGPT芯片算力:研究框架 简介 “AI算力时代已经来临,计算机行业正在经历着一场前所未有的变革!” 这是一个充满活力和兴奋的时代,人工智能(AI)已…...
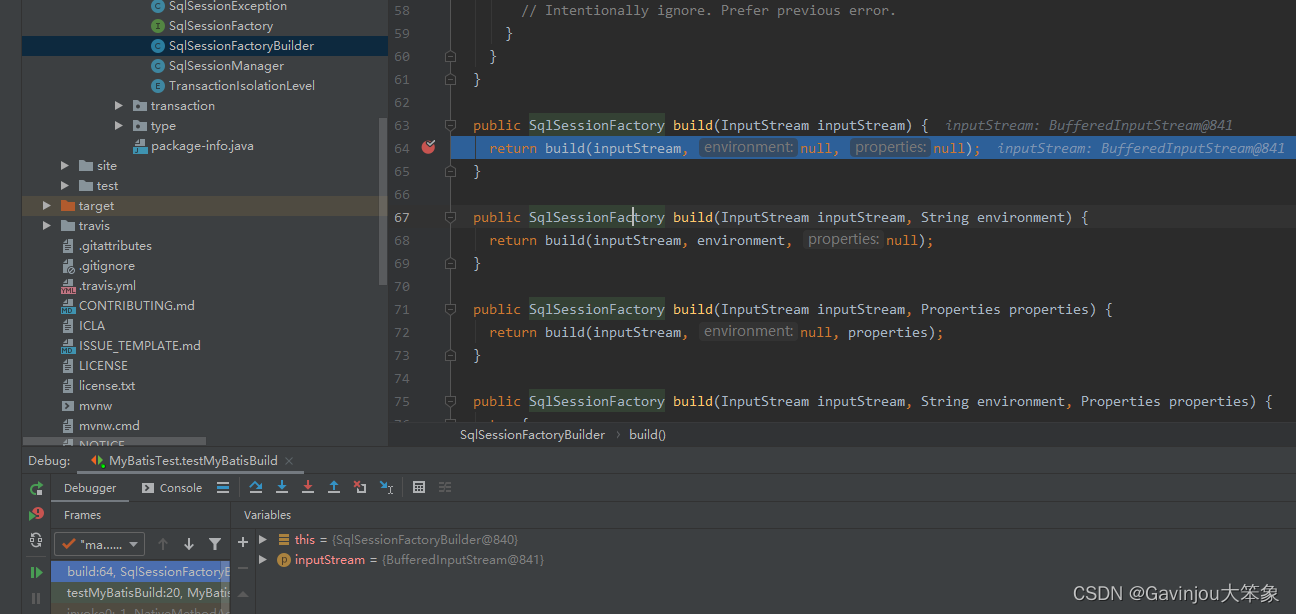
『MyBatis技术内幕』源码调试前提
准备源代码包 下载源代码 3.4.6 版本 https://github.com/mybatis/mybatis-3/releases?page2 通过 idea 导入然后回自动下载所有依赖,根据 3.4.6 版本的 pom.xml 找到依赖的 mybatis-parent 版本 <parent><groupId>org.mybatis</groupId><ar…...

# Linux最新2022年面试题大汇总,附答案
# Linux最新2022年面试题大汇总,附答案 ### [1、cp(copy单词缩写,复制功能)](最新2021年面试题大汇总,附答案.md#1cpcopy单词缩写复制功能) cp /opt/java/java.log /opt/logs/ ;把java.log 复制到/opt/logs/下 cp /…...

css中重难点整理
一、vertical-align 在学习vertical-align的时候,可能会很困惑。即使网上有一大推文章讲veitical-align,感觉看完好像懂了,等自己布局的时候用到vertical-align的时候好像对它又很陌生。这就是我在布局的时候遇到的问题。 本来vertical-align就很不好理…...

JavaScript-扫盲
文章目录1. 前言2. 第一个 JavaScript 程序3. javaScript 的基础语法3.1 变量3.2 数据类型3.3 运算符3.4 条件语句3.5 数组3.6 函数3.7 作用域3.8 对象4. WebAPI4.1 DOM 基本概念4.2 常用 DOM API4.3 事件4.4 操作元素4.5 网页版猜数字游戏4.6 留言版1. 前言 提问 java 和 java…...
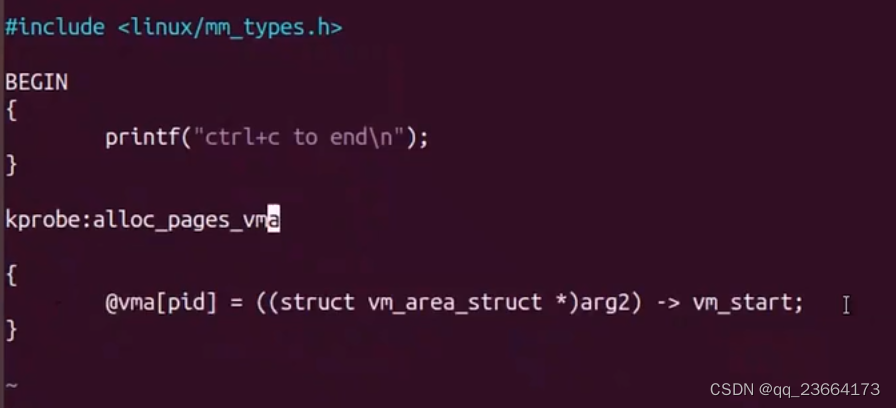
bpftrace 笔记
bpftrace -e BEFIN {printf("hello world!\n");}获取调用 vfs_read 函数的进程id, 每2s打印一次 bpftrace -e kprobe:vfs_read {ID pid;} interval:s:2 {printf{"ID:%d\n", ID);}用户态调试 bpftrace -e uprobe:/*/a.out:and {printf("ID:%d\n&qu…...
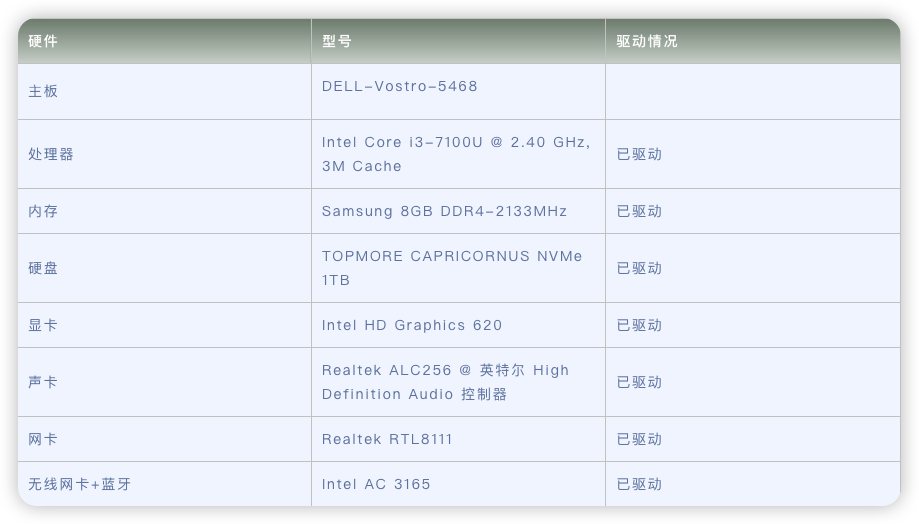
DELL-Vostro-5468电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板DELL-Vostro-5468处理器Intel Core i3-7100U 2.40 GHz, 3M Cache已驱动内存Samsung 8GB DDR4-2133MHz已驱动硬盘TOPMORE CAPRICORNUS NVMe 1TB已驱动显卡Intel HD Graphics 620已驱动声卡Realtek ALC2…...

阶段二11_面向对象高级_学生管理系统案例2
主要内容: 添加学生 static关键字一.添加学生时判断id是否存在 0.思路图片: 04/图片/2_添加学生判断id存在的问题分析.png 1.思路实现详细步骤: StudentController【客服接待】 /** 接收到学生id后,判断该id在数组中是否存在 这…...
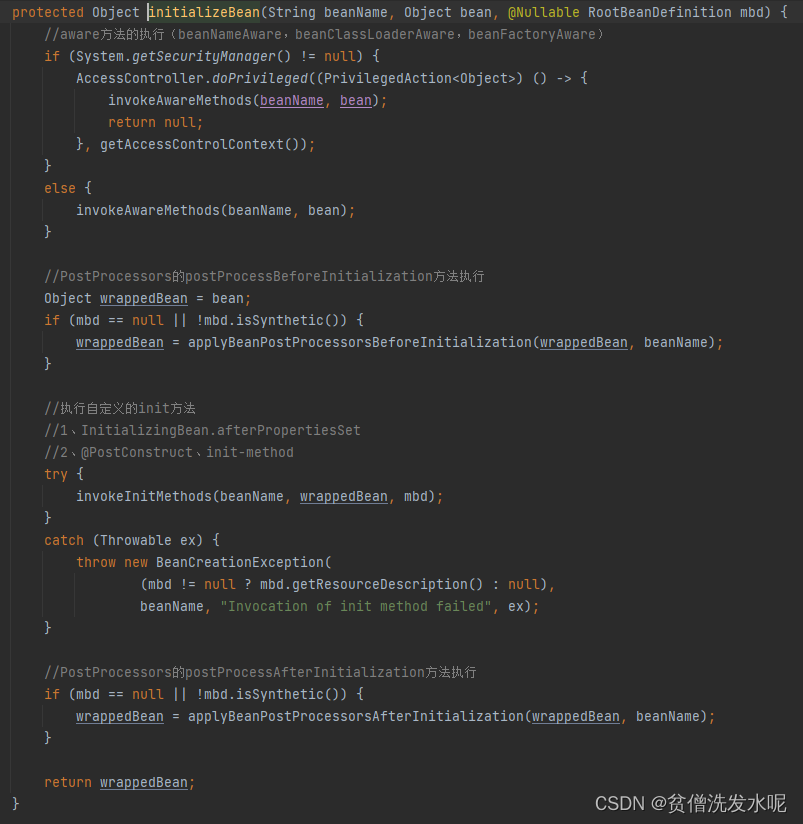
spring源码篇(3)——bean的加载和创建
spring-framework 版本:v5.3.19 文章目录bean的加载bean的创建总结getBean流程createBean流程doCreateBean流程bean的加载 beanFactory的genBean最常用的一个实现就是AbstractBeanFactory.getBean()。 以ApplicationContext为例,流程是: ApplicationCon…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
