学习记录---Python内置类型
文章目录
- 字符串
- split()
- 列表
- 常见操作
- 列表相减
- 字典
- 创建
- 普通创建
- eval(s)
- 添加或更新元素
- d['t'] = 1
- d.update({'c': 3})
- {**d1, **d2} **字典解包装运算符
- 删除元素 d.pop('c')
- 属性
- d.items()
- d.keys()
- d.values()
- 访问元素
- d['Name']
- d.get('score')
- 遍历字典
- for key in dict
- for key, values in dict.items()
- 查询
- 判断是否为空
- 排序
- 按key排序
- 按value排序
- 类似switch的用法
个人学习总结,持续更新中……
字符串
split()
split()方法
str.split(str="", num=string.count(str))
str – 分隔符,默认为所有的空字符,包括空格、换行(\n)、制表符(\t)等。
num – 分割次数。默认为 -1, 即分隔所有。
注意:a.split()和a.split(’ ')是不一样的
a = '122 345'
b = a.split()
print(b)
# ['122', '345']a = '122 345'
b = a.split(' ')
print(b)
# ['122', '', '', '', '', '', '', '345']
列表
常见操作
列表相减
list_1 = [1, 2, 3, 4, 5]
list_2 = [1, 2, 3]print(list(set(list_1) ^ set(list_2)))
'''
[4, 5]
'''
字典
字典键的特性:
1)不允许同一个键出现两次。创建时如果同一个键被赋值两次,后一个键值对会覆盖前一个键值对;
2)键必须不可变,所以可以用数字,字符串或元组充当,而用列表就不行。
创建
普通创建
d1 = dict(a=1, b=2, c=3) # 创建
print('d1: ', d1)
'''
d1: {'a': 1, 'b': 2, 'c': 3}
'''
d2 = dict([('a', 1), ('b', 2), ('c', 3)]) # 创建
print('d2: ', d2)
'''
d2: {'a': 1, 'b': 2, 'c': 3}
'''
d3 = {'a': 1, 'b': 2, 'c': 3} # 创建
print('d3: ', d3)
'''
d4: {'a': 1, 'b': 2, 'c': 3}
'''
d4 = dict(zip(['a', 'b', 'c'], [1, 2, 3]))
print('d4: ', d4)
'''
d4: {'a': 1, 'b': 2, 'c': 3}
'''
eval(s)
# python中有一个内置函数eval
# 字符串为"{'A':123,'B':456,'C':789}"
s = "{'A':123,'B':456,'C':789}"
s_dic = eval(s)
print(s_dic)
# {'A': 123, 'B': 456, 'C': 789}
print(type(s_dic))
# <class 'dict'>
添加或更新元素
d[‘t’] = 1
d = {} # 创建空字典
d['t'] = 1 # 添加元素
d['p'] = 2
d['z'] = 3
print('d: ', d)
# d: {'t': 1, 'p': 2, 'z': 3}
d.update({‘c’: 3})
Python 字典 update() 函数把字典参数 dict的 key/value(键/值) 对更新到字典 dict 里。
如果键相同,则更新值,如果键不同,则添加。
d = dict([('a', 1), ('b', 2)])
d.update({'c': 3})
print(f'd:\n{d}')
# {'a': 1, 'b': 2, 'c': 3}
{**d1, **d2} **字典解包装运算符
如果键相同,则更新值,如果键不同,则添加。
d1 = dict([('a', 1), ('b', 2)])
d2 = {'c': 3}
d3 = {**d1, **d2}
print(d3)
# {'a': 1, 'b': 2, 'c': 3}
删除元素 d.pop(‘c’)
d = dict([('a', 1), ('b', 2), ('c', 3)])
d.pop('c') # 删除元素
print(d)
# {'a': 1, 'b': 2}
属性
d.items()
返回可遍历的(键, 值) 元组数组。
可以list转换为列表
d = dict([('a', 1), ('b', 2)])
print(f'd.items():\n{d.items()}')
'''
d.items():
dict_items([('a', 1), ('b', 2)])
'''
print(f'list(d.items()):\n{list(d.items())}')
'''
list(d.items()):
[('a', 1), ('b', 2)]
'''
a = dict(d.items())
print(f'a:\n{a}')
'''
a:
{'a': 1, 'b': 2}
'''
d.keys()
返回可遍历的键元组数组。
可以list转换为列表
d = dict([('a', 1), ('b', 2)])
print(f'd.keys():\n{d.keys()}')
'''
d.keys():
dict_keys(['a', 'b'])
'''
print(f'list(d.keys()):\n{list(d.keys())}')
'''
list(d.keys()):
['a', 'b']
'''
d.values()
返回可遍历的值元组数组。
可以list转换为列表
d = dict([('a', 1), ('b', 2)])
print(f'd.values():\n{d.values()}')
'''
d.values():
dict_values([1, 2])
'''
print(f'list(d.values()):\n{list(d.values())}')
'''
list(d.values()):
[1, 2]
'''
访问元素
d[‘Name’]
d = {'Name': 'Runoob', 'Age': 7, 'score': 'First'}
print(d['Name'])
# Runoob
d.get(‘score’)
d = {'Name': 'Runoob', 'Age': 7, 'score': 'First'}
print(d.get('score'))
# First
遍历字典
for key in dict
d = {'a': 1, 'b': 2, 'c': 3} # 创建for k in d:print(k, d[k])
'''
a 1
b 2
c 3
'''
for key, values in dict.items()
dict = {'a': 1, 'b': 2, 'c': 3} # 创建for k, v in dict.items():print(k, v)
'''
a 1
b 2
c 3
'''
查询
d = {'a': 1, 'b': 2, 'c': 3} # 创建if 'a' in d:print(d['a'])
# 1
判断是否为空
在python 中 None,空列表[],空元组(),空字典{},0都是被程序判断为False ,所以我们判断对象是否为空可以直接使用if x 或者if not x 的方法来判断对象是否为空。
# 方法一:len()
list1 = {}
if len(list1) == 0:print("dict is empty")
# dict is empty# 方法二:直接使用if判断
list2 = {}
if not list2:print("dict is empty")
# dict is empty# 方法三:使用 空列表进行判断
list3 = {}
emptylist = {}
if list3 == emptylist:print("dict is empty")
# dict is empty
排序
Python教程按照字典的键或值进行排序方法解析
按key排序
dir_info = {'a': 1, 'd': 8, 'c': 3, 'b': 5}
print(dir_info)
# {'a': 1, 'd': 8, 'c': 3, 'b': 5}# 按key排序
dir_sort = sorted(dir_info.items(), key=lambda x: x[0], reverse=False)
print(dir_sort)
# [('a', 1), ('b', 5), ('c', 3), ('d', 8)]
按value排序
dir_info = {'a': 1, 'd': 8, 'c': 3, 'b': 5}
print(dir_info)
# {'a': 1, 'd': 8, 'c': 3, 'b': 5}# 按value排序
dir_sort = sorted(dir_info.items(), key=lambda x: x[1], reverse=True)
print(dir_sort)
# [('d', 8), ('b', 5), ('c', 3), ('a', 1)]
类似switch的用法
def sum1(a):return a + 1def sum2(a):return a + 2def sum3(a):return a + 3sum_kinds = {'sum1': sum1,'sum2': sum2,'sum3': sum3}def sum_cal(sum_k, a):b = sum_kinds[sum_k](a)return bc = sum_cal('sum1', 100)
print(c)
# 101相关文章:

学习记录---Python内置类型
文章目录字符串split()列表常见操作列表相减字典创建普通创建eval(s)添加或更新元素d[t] 1d.update({c: 3}){**d1, **d2} **字典解包装运算符删除元素 d.pop(c)属性d.items()d.keys()d.values()访问元素d[Name]d.get(score)遍历字典for key in dictfor key, values in dict.it…...
Python笔记 -- 列表
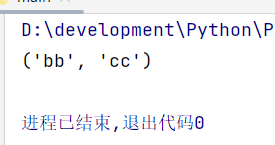
文章目录1、列表简介2、修改、添加、删除元素2.1、添加2.2、删除3、排序、倒序4、遍历列表5、创建数值列表6、列表切片7、列表复制8、元组1、列表简介 在Python中用方括号[]表示列表,用逗号隔开表示其元素 通过索引访问列表 names [aa,bb,cc,dd]print(names[0]) …...

谈谈UVM中的uvm_info打印
uvm_info宏的定义如下: define uvm_info(ID,MSG,VERBOSITY) \begin \if (uvm_report_enabled(VERBOSITY,UVM_INFO,ID)) \uvm_report_info (ID, MSG, VERBOSITY, uvm_file, uvm_line); \end 从这里可以看出uvm_info由两部分组成:uvm_report_enabled(VER…...
)
矩阵理论1 集合上的等价关系(equivalence relations on a set S)
定义 对于一个集合S, 如果集合E⊂SS\mathcal{E} \subset S\times SE⊂SS满足以下条件 自反性: 对于∀s∈S,都有(s,s)∈E\forall s\in S, 都有 (s, s) \in \mathcal{E}∀s∈S,都有(s,s)∈E对称性: (s,t)∈E⇔(t,s)∈E(s,t) \in \mathcal{E} \Leftrightarrow (t,s)\in \mathcal…...
【网络监控】Zabbix详细安装部署(最全)
文章目录Zabbix详细安装部署环境准备安装依赖组件访问初始化配置Zabbix详细安装部署 Zabbix 是一个高度集成的网络监控解决方案,可以提供企业级的开源分布式监控解决方案,由一个国外的团队持续维护更新,软件可以自由下载使用,运作…...

阿里云轻量服务器--Docker--Nacos安装(使用外部Mysql数据存储)
前言:docker 安装nacos 如果不设置外部的mysql 默认使用内嵌的内嵌derby为数据源,这个时候如果,重新部署nacos 则会造成原有数据丢失情况; 1 默认安装的nacos 启动后使用的是内嵌的存储: 2 使用外部mysql 作为存储&a…...
unity开发知识点小结01
unity对象生命周期函数 Awake():最早调用,所以可以实现单例模式 OnEnable():组件激活后调用,在Awake后调用一次 Stat():在Update()之前,OnEnable…...

软件系统[软件工程]
What’s the link? They all involve outdated (legacy) software technology. All have had huge socio-economical impact. Prompting national lockdowns. Spreadsheet workflow error led to thousands of preventable infections and deaths. Huge losses of citizen dat…...
电力系统稳定性的定义与分类
1电力系统稳定性的定义与分类 IEEE给出电力系统稳定性定义:电力系统稳定性是指电力系统这样的一种能力—对于给定的初始运行状态,经历物理扰动后,系统能够重新获得运行平衡点的状态,同时绝大多数系统变量有界,因此整个…...
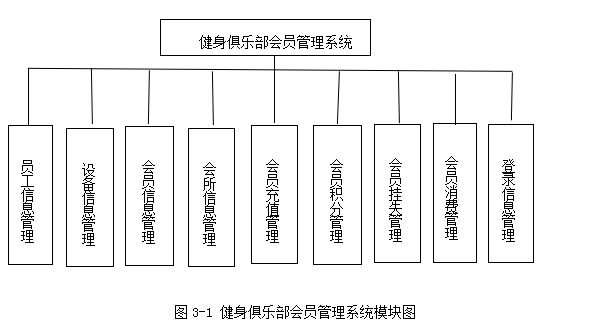
基于java的俱乐部会员管理系统
技术:Java、JSP等摘要:随着科学技术的飞速发展,科学技术在人们日常生活中的应用日益广泛,也给各行业带来发展的机遇,促使各个行业给人们提供更加优质的服务,有效提升各行业的管理水平。俱乐部通过使用一定的…...
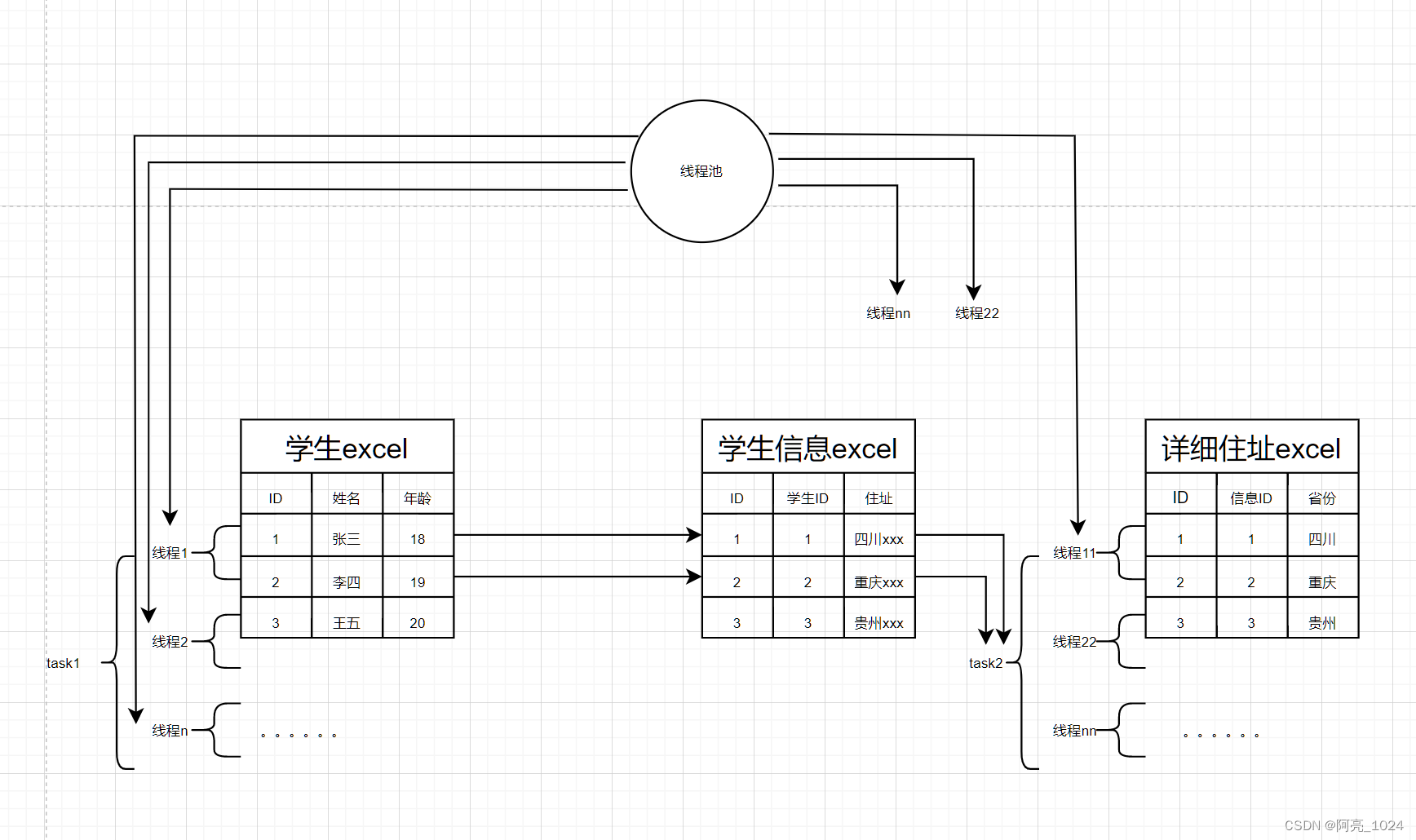
线程池执行父子任务,导致线程死锁
前言, 一次线程池的不当使用,导致了现场出现了线程死锁,接口一直不返回。而且由于这是一个公共的线程池,其他使用了次线程池的业务也一直阻塞,系统出现了OOM,不过是幸好是线程同事测试出来的,没…...
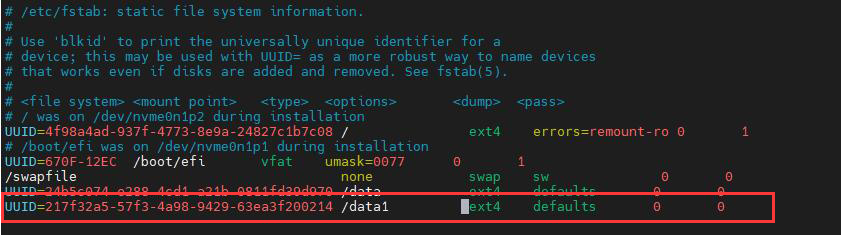
Ubuntu系统新硬盘挂载
Ubuntu系统新硬盘挂载 服务器通常会面临存储不足的问题,大部分服务器都是ubuntu系统,该篇博客浅浅记载一下在ubuntu系统上挂载新硬盘的步骤。本篇博文仅仅记载简单挂载一块新的硬盘,而没有对硬盘进行分区啥的。如果需要更加完善的教程&#…...
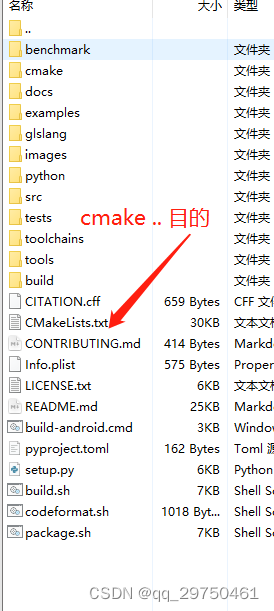
【亲测】Centos7系统非管理(root)权限编译NCNN
前言 由于使用的是集群,自己不具有管理员权限,所以以下所有的情况均在非管理员权限下进行安装,即该安装策略仅适用于普通用户构建自己的环境。 什么是NCNN ncnn是一款非常高效易用的深度学习推理框架,支持各种神经网络模型&#x…...

四种常见的异步请求方式
四种常见的异步请求方式 一、xhr异步老祖 XMLHttpRequest(简称XHR)是一种在JavaScript中创建异步请求的技术。XHR对象可以向服务器发送请求,并获取服务器返回的数据,而不会使页面刷新。 XHR对象的创建方式通常是通过构造…...
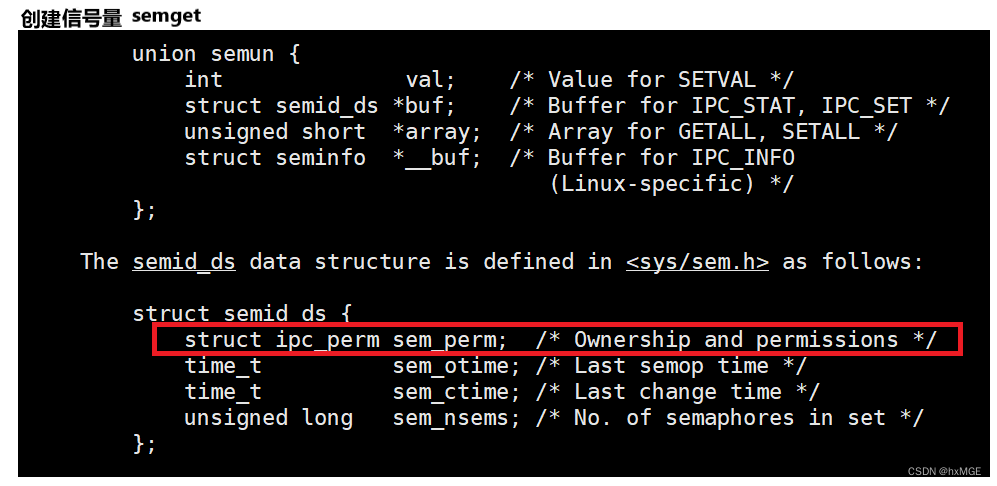
Linux操作系统学习(进程间通信)
文章目录进程间通信进程通信的意义进程通信的方式1.基于文件的方式匿名管道命名管道2.基于内存的通信方式共享内存验证内核相关的数据结构了解进程间通信 进程通信的意义 当我们和另一个人打电话时两部手机都是独立的,通过基站传递信号等等复杂的过程就实现了通…...
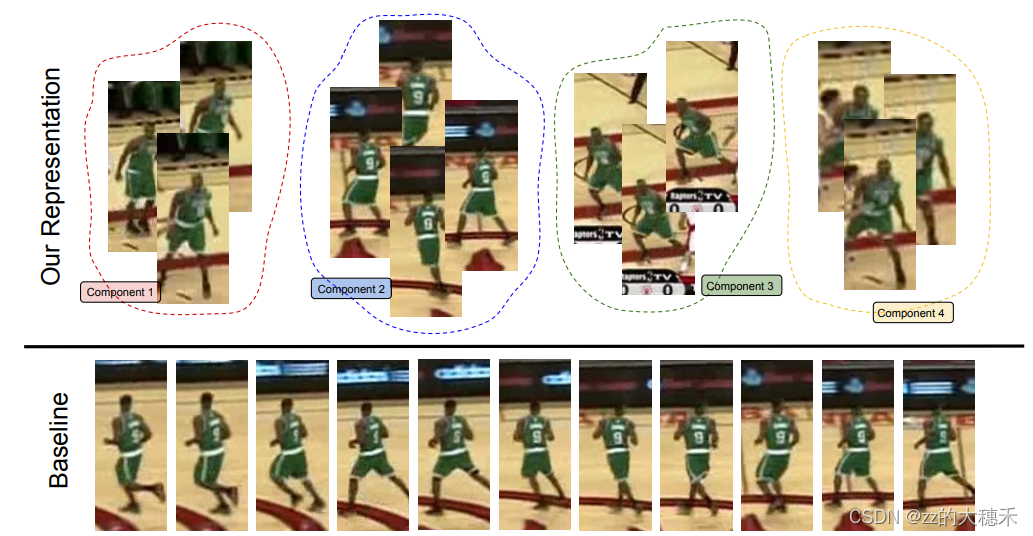
单目标追踪——【相关滤波】C-COT原理与ECO基于C-COT的改进
目录C-COT:Continuous Convolution Operator Tracker文章侧重点连续卷积算子目标追踪框架初始化过滤器:追踪流程ECO文章侧重点因式卷积因子生成采样空间模型模型更新策略论文链接:C-COT:Beyond Correlation Filters: Learning Con…...

C++中栈是如何实现,以及常用的栈函数都有哪些
什么是栈? 栈 是一种特殊的数据结构,它是一种按照 Last-In-First-Out (LIFO) 访问模式存储和访问数据的特殊结构。 换句话说,栈中的最后一个元素将成为最先出栈的元素,这也意味着新增加的元素在栈的顶部,而出栈的元素…...

我就不信你还不懂HashSet/HashMap的底层原理
💥注💥 💗阅读本博客需备的前置知识如下💗 🌟数据结构常识🌟👉1️⃣八种数据结构快速扫盲🌟Java集合常识🌟👉2️⃣Java单列集合扫盲 ⭐️本博客知识点收录于…...
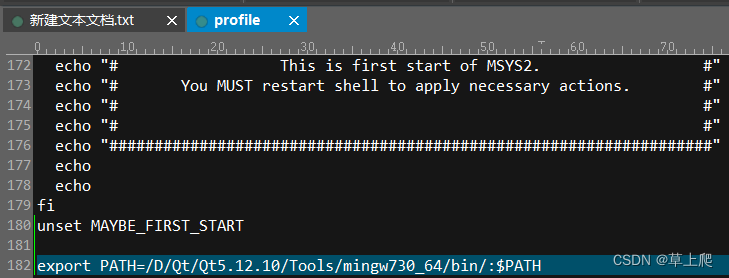
Qt中调用gtest进行单元测试及生成覆盖率报告
一.环境配置 googletest地址:https://github.com/google/googletest 我下载的是1.12.1,这是最后一个支持C++11的版本。 首先编译gtest,在windows上的编译方式和编译gRPC一模一样,详见Qt中调用gRPC,编译完了会生成几个静态库,如下图所示 本文主要用到了libgtest.a 下载ms…...

ChatGPT vs Bard 背后的技术对比分析和未来发展趋势
ChatGPT vs Bard 背后的技术对比分析和未来发展趋势 目录 ChatGPT vs Bard 背后的技术对比分析和未来发展趋势...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
