【蓝桥杯集训·每日一题】AcWing 1488. 最短距离
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- Dijkstra算法
一、题目
1、原题链接
1488. 最短距离
2、题目描述
有 N 个村庄,编号 1 到 N。
村庄之间有 M 条无向道路,第 i 条道路连接村庄 ai 和村庄 bi ,长度是 ci。
所有村庄都是连通的。
共有 K 个村庄有商店,第 j 个有商店的村庄编号是 xj。
然后给出 Q 个询问,第 k 个询问给出一个村庄的编号 yk,问该村庄距离最近的商店有多远?
输入格式
第一行包含两个整数 N,M。
接下来 M 行,每行包含三个整数 ai,bi,ci,表示第 i 条道路连接村庄 ai 和村庄 bi,长度是 ci。
再一行包含整数 K。
接下来 K 行,每行包含一个整数 xj,表示第 j 个有商店的村庄编号是 xj。
再一行包含整数 Q。
接下来 Q 行,每行包含一个整数 yk,表示询问编号为 yk 的村庄与其距离最近的商店之间的距离。
输出格式
对于每个询问,输出该询问的结果。
数据范围
2≤N≤105,N−1≤M≤min(N(N−1)/2,105),1≤Q≤105,1≤K≤N,1≤ci≤10000
输入样例:
7 7 1 2 5 1 4 3 2 3 2 2 5 1 3 6 7 5 6 8 6 7 6 3 7 5 4 7 1 2 3 4 5 6 7输出样例:
3 1 3 0 0 6 0
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
(1)将每个商店看做起点,在图中添加一个虚拟源点(起点),该点到其后面所有商店的距离均为0(有向边),则可以将从村庄走到商店的最短路径转化为从村庄走到源点(也就是从源点到村庄)的最短路径,两者等价。
(2)模拟上述过程,求从虚拟源点到村庄的最短路径,即为从村庄到商店的最短路径。
2、时间复杂度
时间复杂度为O(mlogn)(n表示点数,m表示边数)
3、代码详解
#include <iostream>
#include <queue>
#include <cstring>
#include <utility>
using namespace std;
typedef pair<int,int> PII;
const int N=100010,M=3*N; //N代表点数,M代表边数,因需要为每个起点添加一条由虚拟源点指向的边,所以开成点数3倍
int dist[N]; //存储每个点到虚拟源点的最短路径
int h[N],e[M],w[M],ne[M],idx; //h[]存储每个点第一条边的idx,e[]存储每条边的终点,ne[]存储每条边同起点的下一条边的idx,idx存储边的编号
bool st[N];
int n,m;
//邻接表中添加一条边
void add(int a,int b,int c){e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}
//堆优化dijkstra求最短路
int dijkstra(){memset(dist,0x3f,sizeof dist);priority_queue<PII,vector<PII>,greater<PII>> heap;dist[0]=0;heap.push({0,0});while(!heap.empty()){PII t=heap.top();heap.pop();int ver=t.second;if(st[ver]) continue;st[ver]=true;for(int i=h[ver];i!=-1;i=ne[i]){int j=e[i];if(dist[j]>dist[ver]+w[i]){dist[j]=dist[ver]+w[i];heap.push({dist[j],j});}}}if(dist[n]==0x3f3f3f3f) return -3;else return dist[n];
}
int main(){cin>>n>>m;memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);add(b,a,c);}int k;cin>>k;while(k--){int x;cin>>x;add(0,x,0); //添加一个虚拟源点到每个商店距离为0的有向边}dijkstra();int q;cin>>q;while(q--){int y;cin>>y;cout<<dist[y]<<endl;}return 0;
}
三、知识风暴
Dijkstra算法
- 基本思想:将一个带权有向图中的顶点分成两组,一组是未确定最短路的,一组是已确定最短路的。每次将未确定最短路集合中的点,按照与源点的距离递增加入已确定最短路的集合中,同时每次往已确定最短路集合中加入一个点后,需要用这个点来更新其他点距离源点的距离。当所有点的最短路都已确定,算法结束。
相关文章:

【蓝桥杯集训·每日一题】AcWing 1488. 最短距离
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴Dijkstra算法一、题目 1、原题链接 1488. 最短距离 2、题目描述 有 N 个村庄,编号 1 到 N。 村庄之间有 M 条无向道路,第 i 条道路连接村庄 ai 和村…...
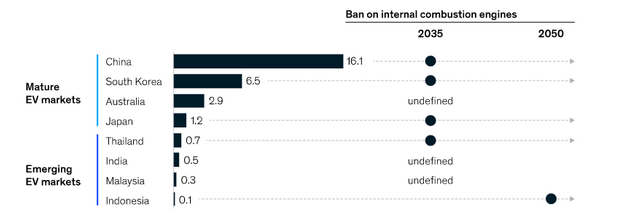
比亚迪:全球最大电动汽车制造商的坎坷成长之路
来源:猛兽财经 作者:猛兽财经 特斯拉(TSLA)首席执行官埃隆马斯克表示,特斯拉最接近的竞争对手可能是一家中国电动汽车公司。猛兽财经认为,沃伦•巴菲特支持的比亚迪(0211)可能是马斯…...

Java开发 - Quartz初体验
前言 在上一篇博客中,我们对单点登录有了初步了解,这也让我们独立做系统有了最基础的保障。但在业务开发中,总是会出现一些定期处理的任务,我们首先想到的是Timer,但由于其调度功能单一,我们实际并不会用它…...
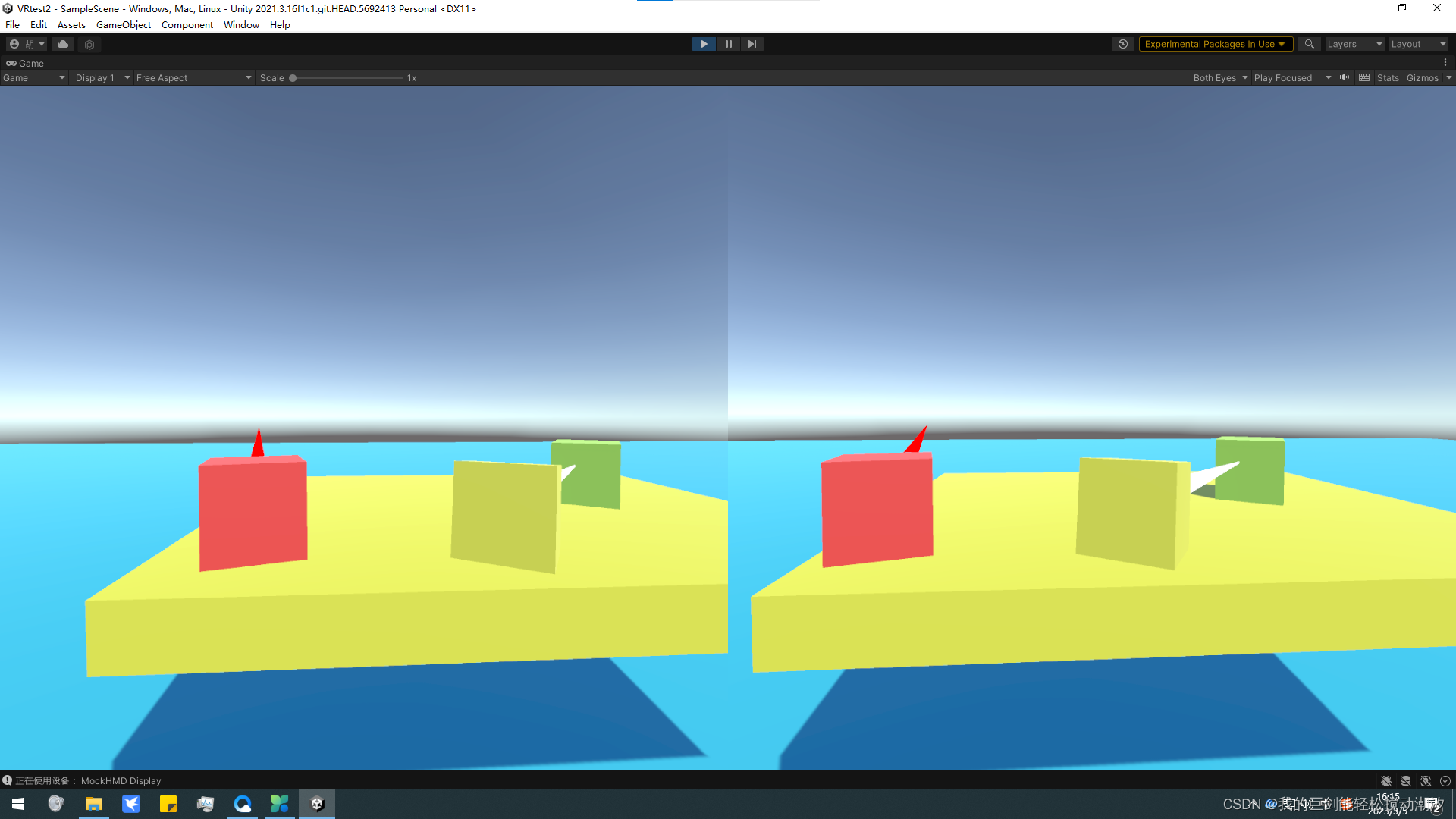
无头盔开发vr XR Device Simulator操作(更新)
1.摄像机(未开启TY键) 平移 上下左右:右键鼠标,移哪去哪 前后:右键快速滚动鼠标滚轮 旋转 XOY平面旋转:右键按住鼠标滚轮滚动鼠标滚轮 XOZ\YOZ平面旋转:右键按住鼠标滚轮移动鼠标 2.左手右手&am…...
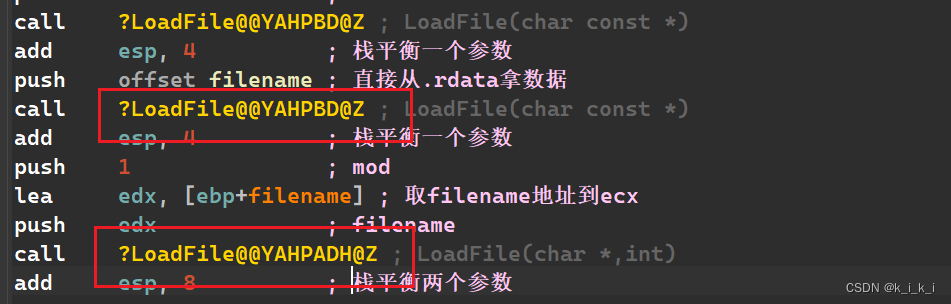
《C++代码分析》第二回:函数重载const char* ,char*,const char[],char[]汇编代码上的区别
一、前言 C相比C是支持函数重载的,现在我们详细探讨一下C函数重载与类方法承载。 二、案例代码 我们编译如下代码,同样的我们关闭代码优化,删除符号链接文(.pdb) #include "windows.h" #include "w…...
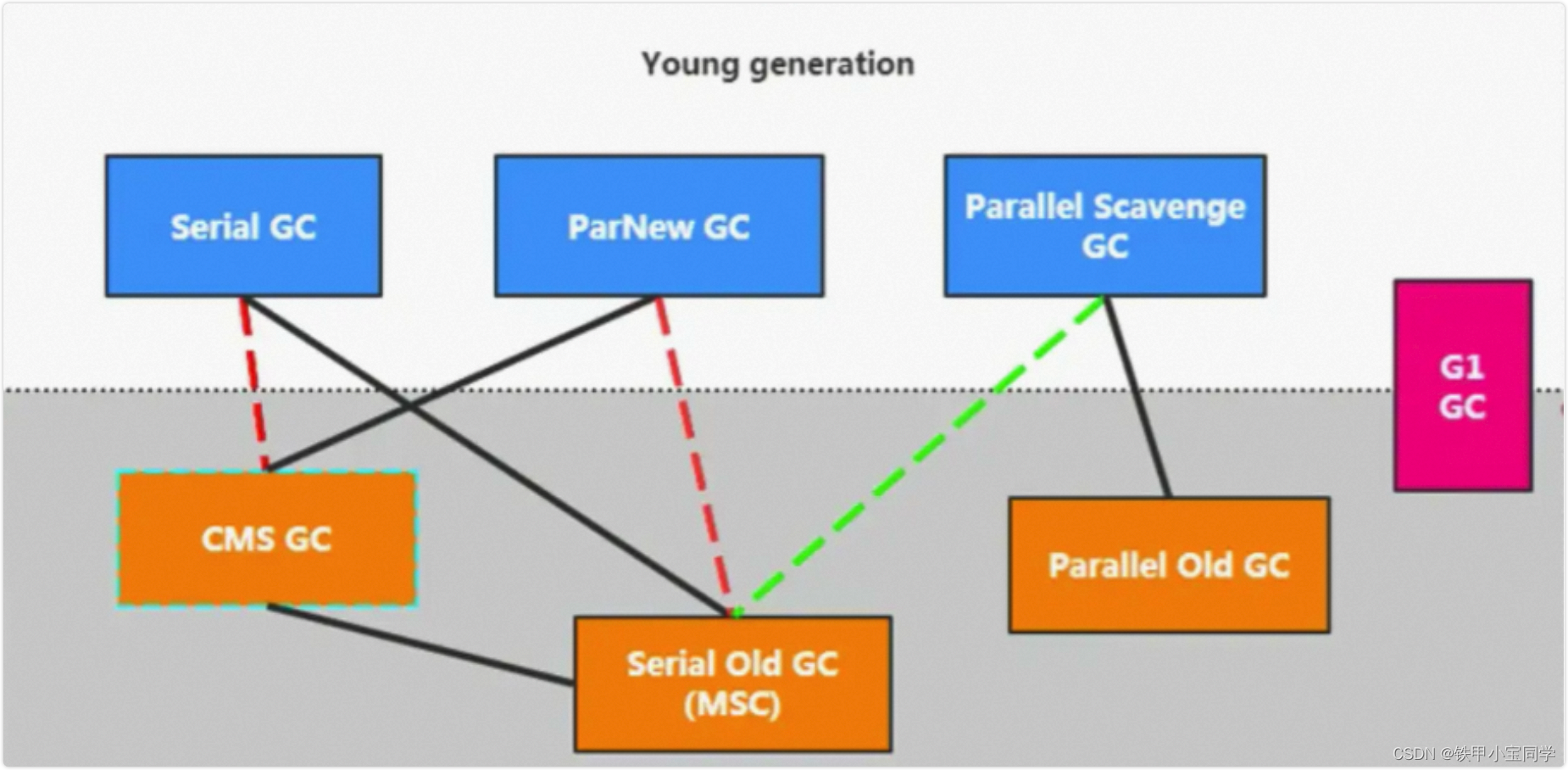
【学习笔记】深入理解JVM之垃圾回收机制
【学习笔记】深入理解JVM之垃圾回收机制 更多文章首发地址:地址 参考: 《深入理解JAVA虚拟机》第三版 第三章尚硅谷 第134 - 203 集参考文章:https://blog.csdn.net/qq_48435252/article/details/123697193 1、概念 🌻 首先我们…...

49.在ROS中实现local planner(2)- 实现Purepersuit(纯跟踪)算法
48.在ROS中实现local planner(1)- 实现一个可以用的模板实现了一个模板,接下来我们将实现一个简单的纯跟踪控制,也就是沿着固定的路径运动,全局规划已经规划出路径点,基于该路径输出相应的控制速度 1. Pur…...
Allegro如何设通孔Pin和Via的消盘操作指导
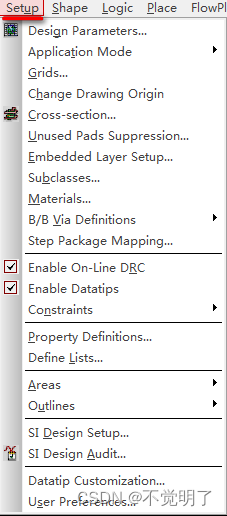
Allegro如何设通孔Pin和Via的消盘操作指导 用Allegro做PCB设计的时候,除了可以在光绘设置里面设置内层通孔Pin和Via的消盘,在设计过程中,同样也可以设置消盘效果,以便实时显示,如下图 如何设置,具体操作如下 点击Setup点击Unused Pads Suppression...
Android工厂模式
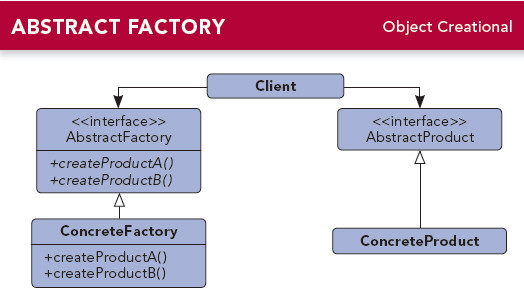
工厂模式分为三种 :简单工厂模式 、工厂方法模式 、抽象工厂模式 。 目录 简单工厂模式 UML图 实现 使用场景: 优点 : 缺点: 工厂方法模式 UML图 实现 使用场景: 优点: 缺点: 抽象工厂模式 UM…...

神经网络硬件加速器-架构篇
架构设计 常规架构通常包括两种: 1、全流水线架构,顾名思义,将整个神经网络进行平铺,并对每一层进行优化设计,优点:实现高吞吐率和低延时。缺点:消耗大量硬件资源,通常无法跨网络或…...
)
Python raise用法(超级详细,看了无师自通)
是否可以在程序的指定位置手动抛出一个异常?答案是肯定的,Python 允许我们在程序中手动设置异常,使用 raise 语句即可。 大家可能会感到疑惑,即我们从来都是想方设法地让程序正常运行,为什么还要手动设置异常呢&#…...
1.SpringSecurity快速入门
*SpringScurity的核心功能: 认证:验证当前访问系统的是不是本系统的用户,并且要确认具体是哪个用户 授权:经过认证后判断当前用户是否有权限进行某个操作 *第一步:创建springboot工程 *第二步:引入SpringSecurity依赖 *第三步:写controller,访问对应的url:localhos…...
Graph Partition: Edge cut and Vertex cut
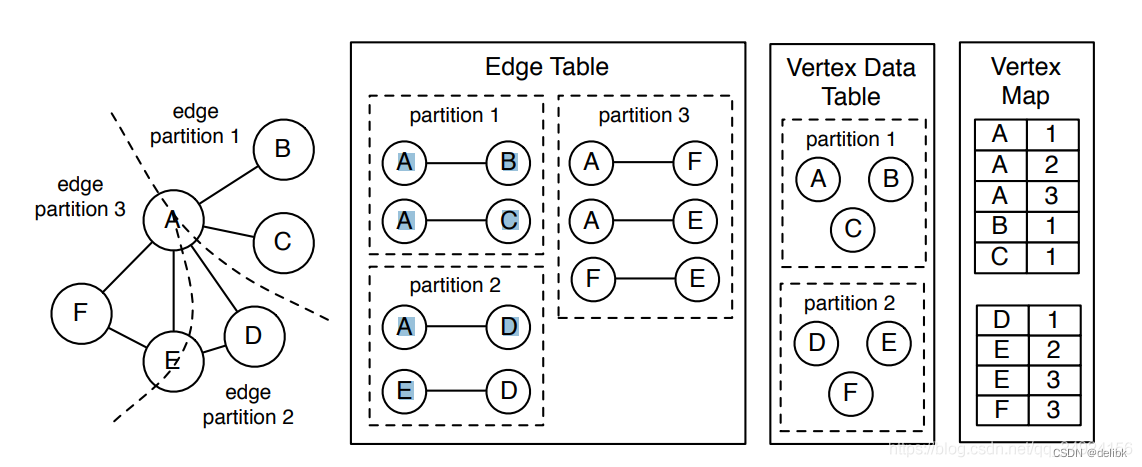
Graph PartitionEdge cut and Vertex cutEdge cutVertex cut实际如何进行点分割和边分割的呢?Graph store format情况1:按照边列表存储:情况2:按照邻接表存储:Edge cut and Vertex cut 图结构描述了数据流动ÿ…...

Javascript周学习小结(初识,变量,数据类型)
JS的三大书写方式行内式如图所示:几点说明:JS的行内式写在HTML的标签内部,(常以on开头),如onclick行内式常常使用单引号括住字符串以区分HTML的双引号可读性差,不建议使用引号易出错,不建议使用特殊情况下使…...
C语言-基础了解-10-C函数
C函数 一、C函数 函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定的,但在逻辑上&…...
【LeetCode】剑指 Offer(16)
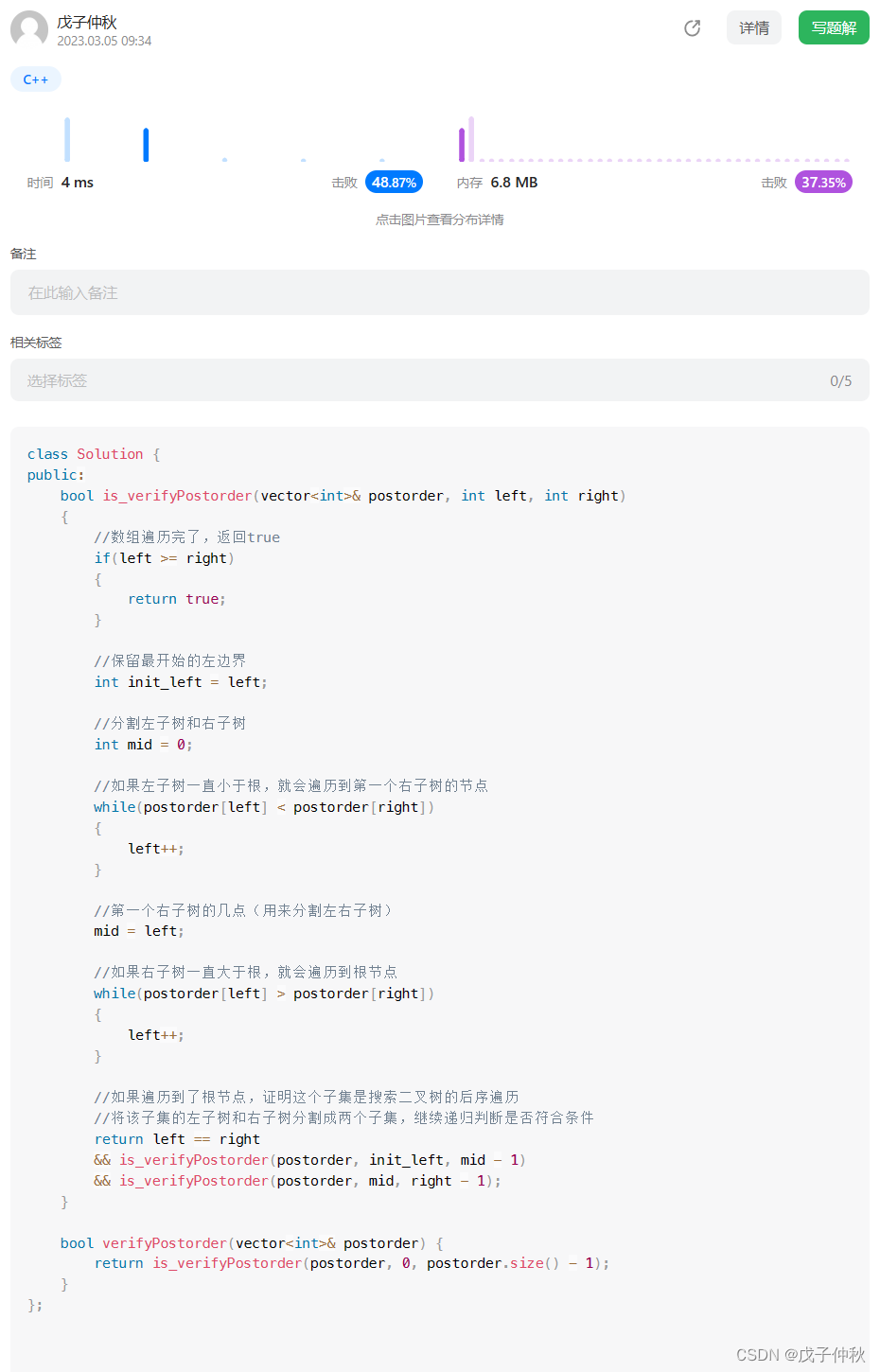
目录 题目:剑指 Offer 33. 二叉搜索树的后序遍历序列 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer …...
)
第三十九章 linux-并发解决方法二(互斥锁mutex)
第三十九章 linux-并发解决方法二(互斥锁mutex) 文章目录第三十九章 linux-并发解决方法二(互斥锁mutex)互斥锁的定义与初始化互斥锁的DOWN操作互斥锁的UP操作用count1的信号量实现的互斥方法还不是Linux下经典的用法,…...

脚本方式本地仓库jar包批量导入maven私服
脚本内容,将以下内容保存为mavenimport.sh,放置于需要上传的目录下,可以是顶层目录,或者某个分包的目录,若私服已有待上传的包,则执行会被替换 #!/bin/bash # copy and run this script to the root of th…...

【c++】引用的学习
引用的定义和声明 引用是一种别名,它允许使用与原变量相同的内存位置。在C中,引用是使用&符号来定义的。引用必须在定义时初始化,并且可以与原变量分别使用。 int a 10; int& b a; // 定义了一个引用b,它指向a引用的作用…...

linux 软件安装及卸载
1.联网在线安装及卸载ubuntu环境下:使用apt-get 工具apt-get install - 安装软件包apt-get remove - 移除(卸载)软件包CentOS环境下:使用yum工具 (银河麒麟系统属于centos)yum install - 安装软件包yum rem…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
