leetCode刷题 5.最长回文子串
目录
1. 思路
2. 解题方法
3. 复杂度
4. Code
题目:
给你一个字符串
s,找到s中最长的回文子串。如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。示例 2:
输入:s = "cbbd" 输出:"bb"提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
1. 思路
要找到字符串 s 中的最长回文子串,我们可以尝试不同的方法。一种常见的方法是使用动态规划。我们定义一个二维数组 dp,其中 dp[i][j] 表示从索引 i 到索引 j 的子串是否是回文串。根据动态规划的思想,我们可以从长度较短的子串开始,逐步扩展到长度较长的子串,并记录下最长的回文子串。
2. 解题方法
- 定义一个二维数组 dp,其中 dp[i][j] 表示从索引 i 到索引 j 的子串是否是回文串。
- 初始化 dp 数组,所有长度为 1 的子串都是回文串,相邻字符相同的子串也是回文串。
- 遍历字符串,根据动态规划的定义填充 dp 数组。
- 在计算 dp 数组的过程中,记录下最长的回文子串的起始位置和长度。
- 返回最长的回文子串。
3. 复杂度
- 时间复杂度:O(n^2),其中 n 是字符串的长度。动态规划需要填充一个二维数组,每个位置需要 O(1) 的时间复杂度。
- 空间复杂度:O(n^2),需要一个二维数组来存储动态规划的结果。
4. Code
class Solution {public String longestPalindrome(String s) {if (s == null || s.length() < 1) return "";int n = s.length();// 定义二维数组 dp,dp[i][j] 表示从索引 i 到索引 j 的子串是否是回文串boolean[][] dp = new boolean[n][n];int start = 0, maxLength = 1;// 初始化 dp 数组,所有长度为 1 的子串都是回文串for (int i = 0; i < n; i++) {dp[i][i] = true;}// 遍历字符串,计算 dp 数组for (int len = 2; len <= n; len++) {for (int i = 0; i <= n - len; i++) {int j = i + len - 1;// 如果当前子串的头尾字符相同,并且内部子串也是回文串,则当前子串是回文串if (s.charAt(i) == s.charAt(j) && (len == 2 || dp[i + 1][j - 1])) {dp[i][j] = true;// 更新最长回文子串的起始位置和长度if (len > maxLength) {start = i;maxLength = len;}}}}// 返回最长回文子串return s.substring(start, start + maxLength);}
}
这段代码使用动态规划的方法,实现了找到字符串中最长的回文子串。通过填充一个二维数组 dp,记录从每个位置开始到每个位置结束的子串是否是回文串,并根据动态规划的结果找到最长的回文子串。
欢迎大家后台联系讨论。

相关文章:

leetCode刷题 5.最长回文子串
目录 1. 思路 2. 解题方法 3. 复杂度 4. Code 题目: 给你一个字符串 s,找到 s 中最长的回文子串。 如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。 示例 1: 输入:s "babad" 输出&#x…...

计算机组成原理面试题
计算机组成原理是计算机科学的基础课程之一,涉及计算机系统的基本结构和工作原理。以下是一些可能出现在面试中的计算机组成原理相关题目: 1. **什么是冯诺依曼体系结构?** - 冯诺依曼体系结构是一种计算机组织架构,它将程序指…...

「Mybatis深入三」:高级查询-模糊查询
一、需求 根据username 模糊查询user 表 二、代码演示 1、方式1 数据库环境 CREATE DATABASE mybatis_db; USE mybatis_db; CREATE TABLE user (id INT(11) NOT NULL AUTO_INCREMENT,username VARCHAR(32) NOT NULL COMMENT 用户名称,birthday DATETIME DEFAULT NULL COMMEN…...

LabVIEW管道缺陷智能检测系统
LabVIEW管道缺陷智能检测系统 管道作为一种重要的输送手段,其安全运行状态对生产生活至关重要。然而,随着时间的推移和环境的影响,管道可能会出现老化、锈蚀、裂缝等多种缺陷,这些缺陷若不及时发现和处理,将严重威胁到…...
java在cmd中乱码的问题解决
本文深入探讨了在使用 Java 命令行(cmd)时可能出现的中文乱码问题,并提供了两种解决方案。首先,通过临时的方式,用户可以执行命令 chcp 936 选择字符集,然后再运行 Java 命令,确保在选择字符集过…...
OpenHarmony教程指南—ArkUI中组件、通用、动画、全局方法的集合
介绍 本示例为ArkUI中组件、通用、动画、全局方法的集合。 本示例使用 Tabs容器组件搭建整体应用框架,每个 TabContent内容视图 使用 div容器组件 嵌套布局,在每个 div 中使用 循环渲染 加载此分类下分类导航数据,底部导航菜单使用 TabCont…...

第二证券|金价逼近历史高点 黄金股价值有望重估
经过两个多月的震荡后,黄金打响新一波攻势,期货商场价格已逼近前史高点。 有分析认为,虽然黄金价格短期已有显着涨幅,存在震荡或许,但中长时间看,跟着美联储钱银政策的转向,黄金价格仍有上行动…...

关于51单片机晶振定时问题
单片机中晶振频率为12MHZ的机器周期怎么算? 1、系统晶振频率是12M,则机器周期=12/12=1us; 2、定时1ms=1*1000=1000us; 3、工作在方式1下:最大计数值是2&a…...
NoSQL--2.MongoDB配置(Windows版)
目录 2.MongdoDB配置 2.1 Windows环境下操作 2.1.1 注册MongDB Atlas: 2.1.2 MongoDB Community Server Download: 2.1.3 启动MondgoDB服务: 2.1.3.1 命令行参数的方式启动MongoDB服务: 2.1.3.2 使用配置文件方式启动Mongo…...

HTML静态网页成品作业(HTML+CSS)——安徽宣笔设计制作(5个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有6个页面。 🏷️想要…...

MySQL CTEs通用表表达式:进阶学习-递归查询
MySQL CTEs通用表表达式:进阶学习-递归查询 递归通用表表达式是其会引用自身的通用表表达式。 CTEs 递归通用表表达式补上了MySQL8之前无法使用递归查询的空白。在之前,递归查询需要使用函数等方法实现。 基础使用,请参考前文: …...
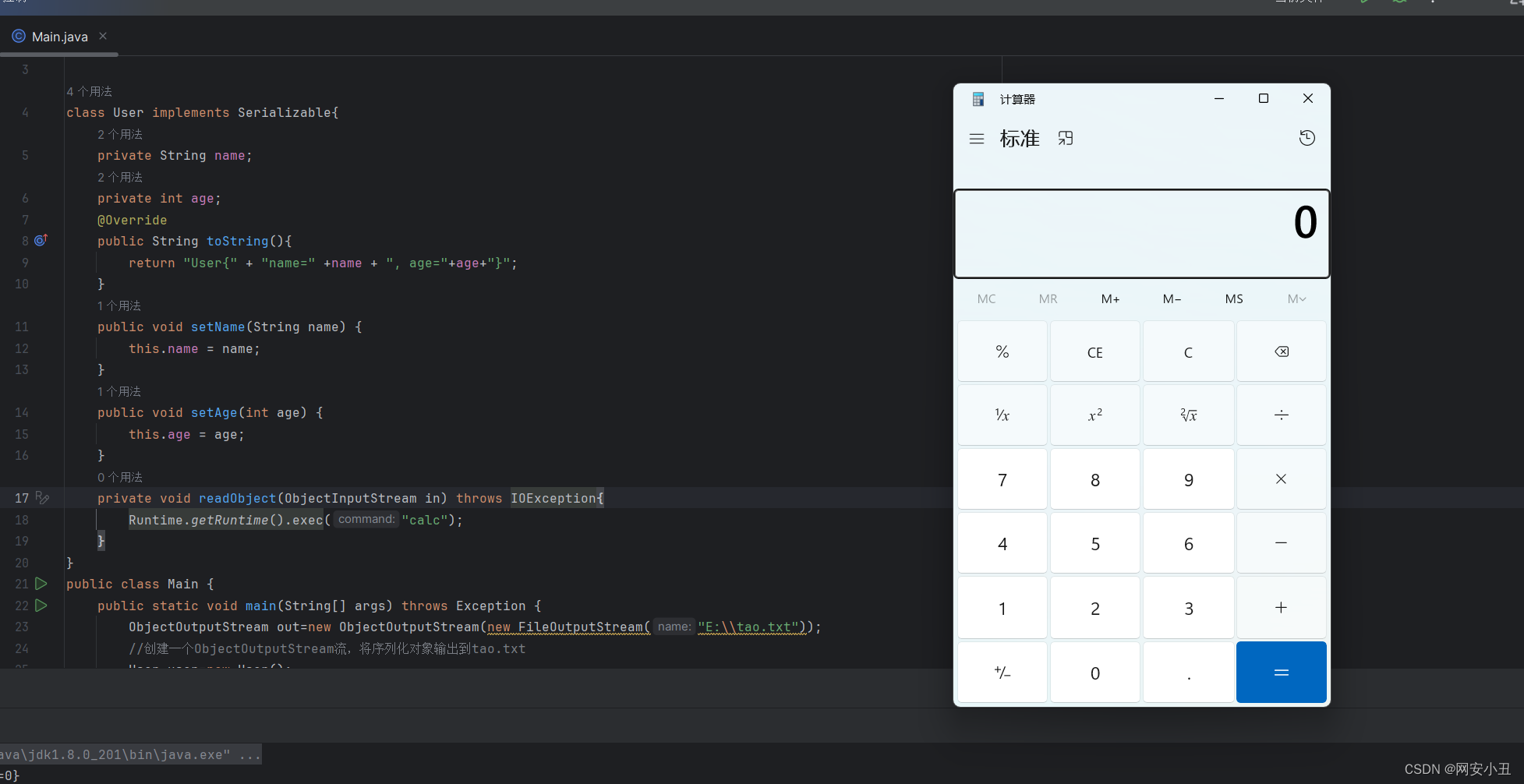
[Java安全入门]二.序列化与反序列化
一.概念 Serialization(序列化)是一种将对象以一连串的字节描述的过程;反序列化deserialization是一种将这些字节重建成一个对象的过程。将程序中的对象,放入文件中保存就是序列化,将文件中的字节码重新转成对象就是反…...

Dutree:Linux 文件系统磁盘使用追踪工具
在 Linux 系统中,对文件系统的磁盘使用情况进行跟踪和管理是至关重要的。dutree 是一个功能强大的工具,它能够以可视化的方式展示文件系统中的目录和文件的大小,帮助用户更好地了解磁盘空间的使用情况。本文将介绍 dutree 工具的使用方法、功…...

http和https的区别是什么?
–前言 传输信息安全性不同、连接方式不同、端口不同、证书申请方式不同 一、传输信息安全性不同 1、http协议:是超文本传输协议,信息是明文传输。如果攻击者截取了Web浏览器和网站服务器之间的传输报文,就可以直接读懂其中的信息。 2、h…...

学习Android的第十九天
目录 Android ExpandableListView 分组列表 ExpandableListView 属性 ExpandableListView 事件 ExpandableListView 的 Adapter 范例 参考文档 Android ViewFlipper 翻转视图 ViewFlipper 属性 ViewFlipper 方法 为 ViewFlipper 加入 View 例子:全屏幕可…...

C#上位机调试经验
1.使用Visual Studio的远程工具 因为上位机软件安装在工控机上,不方便调试。如果直接把代码放在工控机上,又不太安全。 可以在工控机上安装一个Visual Studio的远程工具,把随身带的笔记本电脑通过网线插在工控机上 这样可以在笔记本上使用…...

BUUCTF---[极客大挑战 2019]BabySQL1
1.这道题和之前做的几道题是相似的,这道题考的知识点更多。难度也比之前的大一些 2.尝试万能密码 or 1#发现过滤了or,使用1和1,发现他对单引号也进行了过滤。于是我尝试进行双写绕过,发现可以通过了。 3.由之前的做题经验可知,这道题会涉及到…...
0基础跨考计算机|408保姆级全年计划
我也是零基础备考408! 虽说是计算机专业,但是本科一学期学十几门,真的期末考试完脑子里什么都不进的...基本都是考前一周发疯学完水过考试...😅 想要零基础跨考可以直接从王道开始!跟教材一点一点啃完全没必要🥸 现在…...
C# 操作LiteDB
1、很简单的东西不废话,直接上图上代码。 2、NuGet程序中根据自己的项目版本安装LiteDB,如下图: 3、程序运行加过如下图: 4、程序代码如下: using System; using System.Collections.Generic; using System.Linq; using System…...

LeetCode 2917.找出数组中的 K-or 值:基础位运算
【LetMeFly】2917.找出数组中的 K-or 值:基础位运算 力扣题目链接:https://leetcode.cn/problems/find-the-k-or-of-an-array/ 给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。 nums 中的 K-or 是一个满足以下条件的非负整数: 只有…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
