洛谷 P8816 [CSP-J 2022] 上升点列(T4)
目录
题目传送门
算法解析
最终代码
提交结果
尾声
题目传送门
[CSP-J 2022] 上升点列 - 洛谷![]() https://www.luogu.com.cn/problem/P8816
https://www.luogu.com.cn/problem/P8816
算法解析
k = 0 且 xi, yi 值域不大时,这题是非常简单的 DP,类似「数字三角形」。
记 dp(x,y) 为「以 (x,y) 为终点,最长合法序列的长度」。
则对于所有(已经存在的)整点,有:
dp(x,y) = max {dp(x − 1, y), dp(x, y − 1)} + 1
xi, yi 值域比较大时:
可以考虑记 dp(n) 表示「以 n 号点结尾的合法序列,最长能有多长」。
dp(n) = max {dp(i) + 1}
i → n ✓
不会存在环状结构——因为合法序列必须向右、上方发展。
把刚刚的DP改造一下,就是本题正解:
记 dp(n, k) 表示「以 n 号点结尾,已经使用掉了 k 个自由点,获得的收益」。
dp(n,k) = max {dp(i, k − cost) + cost + 1}
i → n ✓
实现细节:本题的求值顺序值得注意,合法路径可能形如 P1 → P3 → P2。
有两种解决方法:
- 记忆化搜索(记忆化搜索最擅长解决求值顺序混乱的 DP)
- 预先按 x, y 排序,使得编号大的点一定是从编号小的点转移过来
这里记忆化搜索比较好写一些,我这里就只讲记忆化搜索了
先写一下求 a 到 b 需要补多少个点的函数,即两点曼哈顿距离再减一(a 在左下,b 在右上,否则返回无穷)
代码中 x[u] 表示 u 点的横坐标,y[u] 表示 u 点的纵坐标
int dis(int a, int b) {if(x[a] > x[b])return inf;if(y[a] > y[b])return inf;return x[b] - x[a] + y[b] - y[a] - 1;
}然后是 dp 函数,定义上面已经说过了
int dp(int now, int k)首先判断如果自由点已经用完了,即 k < 0,那么返回负无穷(因为最后是取最大值)
int dp(int now, int k) {if(k < 0)return -inf;
}既然是记忆化,那么就需要记忆
用 vis[n][k] 数组记录 dp(n, k) 是否访问过,val[n][k] 数组记录如果访问过的 dp(n, k) 的值
这样如果 vis[now][k] == true(访问过),则返回 val[now][k]
int dp(int now, int k) {if(k < 0)return -inf;if(vis[now][k])return val[now][k];
}然后就该枚举它的前驱(代码中的 to),然后取里面最大的收益
这个记录最大收益的变量(代码中的 res)的初值一定要是 1,因为如果哪也去不了,那么就只能走到现在这一个点,也就是 now
int dp(int now, int k) {if(k < 0)return -inf;if(vis[now][k])return val[now][k];int res = 1;for(int to = 1; to <= n; ++to)return res;
}接下来需要判断 to != now,然后计算出 to 到 now 需要补多少个点(代码中的 cost)
int dp(int now, int k) {if(k < 0)return -inf;if(vis[now][k])return val[now][k];int res = 1;for(int to = 1; to <= n; ++to)if(to != now) {int cost = dis(to, now);}return res;
}再判断费用超出运算,就 contunue(如果走不到,dis 就会返回无穷,一定大于 k,所以不用特判走不到)
int dp(int now, int k) {if(k < 0)return -inf;if(vis[now][k])return val[now][k];int res = 1;for(int to = 1; to <= n; ++to)if(to != now) {int cost = dis(to, now);if(cost > k)continue;}return res;
}接着就是往下递归了,now 变成了 to,预算费用还剩 k - cost,所以传进去是
dp(to, k - cost)然后长度还需要加上 to 到 now 的距离,即 cost + 1,然后更新最大值(代码里的 res)
代码中的 bemax 函数是把第一个参数赋成两个参数的最大值用的,具体实现方法就是用一个三目运算符
void bemax(int &a, int b) {a = a > b ? a : b;
}int dp(int now, int k) {if(k < 0)return -inf;if(vis[now][k])return val[now][k];int res = 1;for(int to = 1; to <= n; ++to)if(to != now) {int cost = dis(to, now);if(cost > k)continue;bemax(res, dp(to, k - cost) + cost + 1);}return res;
}最后再将 vis[now][k] 设成 true,val[now][k] 设成 res
最后 return res 就行了
int dp(int now, int k) {if(k < 0)return -inf;if(vis[now][k])return val[now][k];int res = 1;for(int to = 1; to <= n; ++to)if(to != now) {int cost = dis(to, now);if(cost > k)continue;bemax(res, dp(to, k - cost) + cost + 1);}vis[now][k] = true;val[now][k] = res;return res;
}主函数里需要枚举 i = 1 ~ n,j = 0 ~ k,然后传进去(n 为点的个数,k 为自由点的个数)
注意长度还需要加上没用的 k - j 个点,然后更新答案(代码中的 ans)
for(int i = 1; i <= n; ++i)for(int j = 0; j <= k; ++j)bemax(ans, dp(i, j) + k - j);最后输出 ans 即可
最终代码
#include <cstdio>
#define N 1005
using namespace std;const int inf = 0x7fffffff;int n, k;
int x[N], y[N];
bool vis[N][N];
int val[N][N];
int ans;void bemax(int &a, int b) {a = a > b ? a : b;
}int dis(int a, int b) {if(x[a] > x[b])return inf;if(y[a] > y[b])return inf;return x[b] - x[a] + y[b] - y[a] - 1;
}int dp(int now, int k) {if(k < 0)return -inf;if(vis[now][k])return val[now][k];int res = 1;for(int to = 1; to <= n; ++to)if(to != now) {int cost = dis(to, now);if(cost > k)continue;bemax(res, dp(to, k - cost) + cost + 1);}vis[now][k] = true;val[now][k] = res;return res;
}int main() {scanf("%d%d", &n, &k);for(int i = 1; i <= n; ++i)scanf("%d%d", &x[i], &y[i]);for(int i = 1; i <= n; ++i)for(int j = 0; j <= k; ++j)bemax(ans, dp(i, j) + k - j);printf("%d\n", ans);return 0;
}提交结果
提交一下哈
㇏(〃'▽'〃)㇀ AC ! ! !
尾声
如果这篇博客对您(您的团队)有帮助的话,就帮忙点个赞,加个关注!
最后,祝您(您的团队)在 OI 的路上一路顺风!!!
┬┴┬┴┤・ω・)ノ Bye~Bye~
相关文章:

洛谷 P8816 [CSP-J 2022] 上升点列(T4)
目录 题目传送门 算法解析 最终代码 提交结果 尾声 题目传送门 [CSP-J 2022] 上升点列 - 洛谷https://www.luogu.com.cn/problem/P8816 算法解析 k 0 且 xi, yi 值域不大时,这题是非常简单的 DP,类似「数字三角形」。 记 dp(x,y) 为「以 (x,y) …...
python爬虫(2)
继上节 查看数组维数 可以使用数组的ndim属性 代码示例如下: import numpy as np c np.random.randint(1,9,5) print(c.ndim) 结果如下: 当然这些也可以结合前面的各种用法来使用 1、选取数组元素 (1)一维数组的元素…...
外包干了8天,技术退步明显。。。。。
先说一下自己的情况,本科生,19年通过校招进入杭州某软件公司,干了接近3年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
浅谈去耦电容的作用、选择、布局及其它电容的区别!
在一些文章资料中,去耦电容器被认为是旁路电容器。在其他资料中,去耦电容和旁路电容的区别在于:“旁路电容以输入信号中的干扰为滤波对象,而去耦电容以输出信号的干扰为滤波对象,防止干扰信号返回到输出端。”力量。”…...
抖音视频评论批量采集软件|视频下载工具
《轻松搞定!视频评论批量采集软件,助您高效工作》 在短视频这个充满活力和创意的平台上,了解用户评论是了解市场和观众心声的重要途径之一。为了帮助您快速获取大量视频评论数据,我们推出了一款操作便捷、功能强大的软件ÿ…...

javaSE-----继承和多态
目录 一.初识继承: 1.1什么是继承,为什么需要继承: 1.2继承的概念与语法: 二.成员的访问: 2.1super关键字 2.2this和super的区别: 三.再谈初始化: 小结: 四.初识多态: 4.1多…...

数据库之Oracle数据导入导出
目录 一、单表导出和导入1、单表导出数据2、单表导入数据二、全表导出和导入1、远程导出全表数据2、导入本地数据三、密码带特殊字符的写法1、Windows OS写法2、Linux/Unix OS写法 四、总结 一、单表导出和导入 1、单表导出数据 --导出远程服务上的表数据 exp 用户名/密码IP…...

nRF52832——GPIOTE与外部中断
这里写目录标题 GPIOTE 原理分析GPIOTE 输入事件应用GPIOTE 事件寄存器应用GPIOTE 事件组件的应用(库函数)GPIOTE PORT 事件应用 GPIOTE 任务应用GPIOTE 任务触发 LED 寄存器操作组件方式进行任务配置 GPIOTE 原理分析 GPIO 任务和时间(GPIO…...
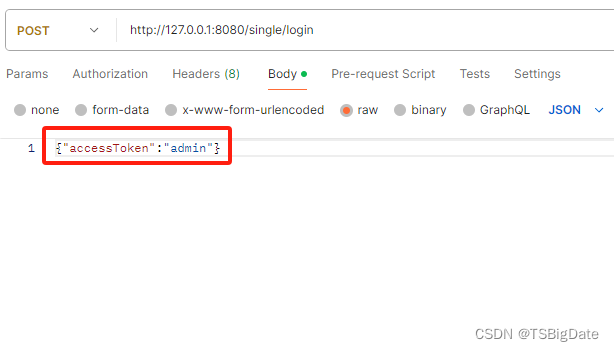
根据用户名称实现单点登录
一、参数格式 二、后端实现 Controller层 public class IAccessTokenLoginController extends BaseController {Autowiredprivate ISysUserService sysUserService;Autowiredprivate ISingleTokenServiceImpl tokenService;/*** 登录方法** return 结果*/PostMapping("/l…...

【设计】855. 考场就座
855. 考场就座 这段代码实现了一个考场安排座位的算法。在这个算法中,考场被模拟成一个从0到n-1的数轴,其中每个位置代表一个座位。目的是在每次学生入座时,找到一个使得所有学生之间距离最大化的座位,并在学生离开时更新座位信息…...
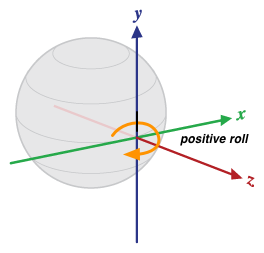
Android中的传感器类型和接口名称
本文将介绍传感器坐标轴、基础传感器和复合传感器(动作传感器、姿势传感器、未校准传感器和互动传感器)。 1. 传感器坐标轴 许多传感器的传感器事件值在相对于设备静止的特定坐标系中表示。 1.1 移动设备坐标轴 Sensor API 仅与屏幕的自然方向相关&a…...

解析进程 /proc/pid/maps 和 /proc/pid/smaps
目录 /proc//maps 背景 具体描述 代码实现 实践 /proc/pid/smaps smaps各子项详解 代码实现 代码调用的路径如下: 小结 /proc/<pid>/maps 背景 相对于/proc/meminfo和dumpsys meminfo可以看到系统整体的内存信息,我们还需要能够具体到…...
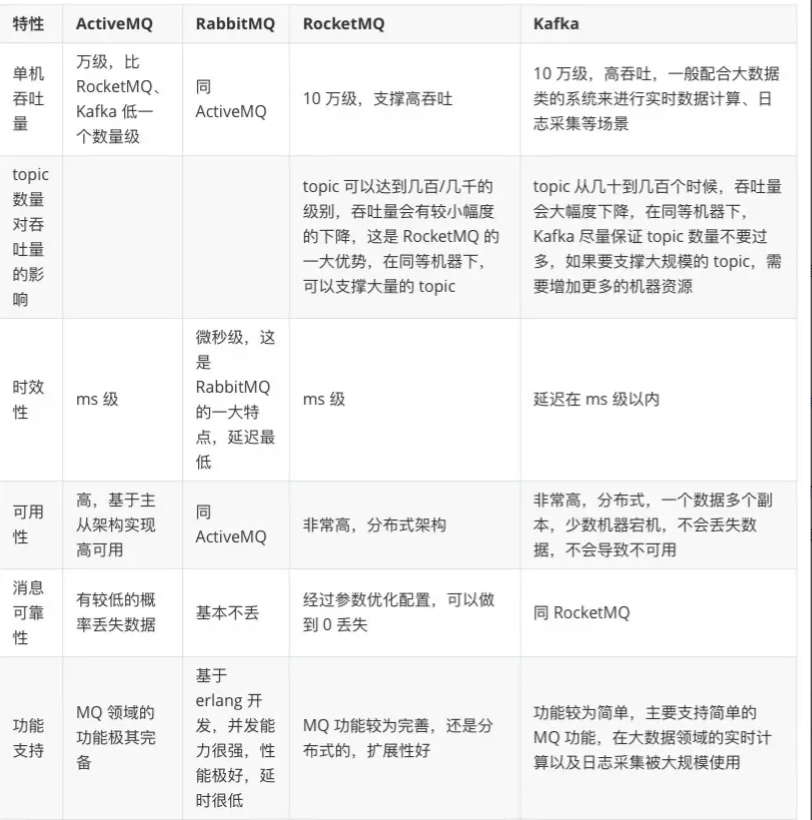
【MQ】消息队列概述
📝个人主页:五敷有你 🔥系列专栏:MQ ⛺️稳中求进,晒太阳 定义 消息队列:一般我们简称为MQ(Message Queue) Message Queue :消息队列中间件,很多初学者认为,MQ通过消息的发送…...
交友盲盒系统PHP开源的盲盒源码
源码介绍: 交友盲盒系统是一款基于PHP开发的开源免费盲盒系统,旨在为用户提供一个充满乐趣和惊喜的社交体验。该系统具有丰富的功能和灵活的扩展性,可以轻松地满足各种线上交友、抽奖活动等场景的需求。 安装说明: PHP版本&…...

【Flutter 面试题】什么是异步编程 Flutter中如何处理异步操作?
【Flutter 面试题】什么是异步编程 Flutter中如何处理异步操作? 文章目录 写在前面解答补充说明从网络API异步获取数据并解析 写在前面 关于我 ,小雨青年 👉 CSDN博客专家,GitChat专栏作者,阿里云社区专家博主&#x…...

处理error: remote origin already exists.及其Gitee文件上传保姆级教程
解决error: remote origin already exists.: 删除远程 Git 仓库 git remote rm origin 再添加远程 Git 仓库 git remote add origin (HTTPS) 比如这样: 然后再push过去就ok了 好多人可能还是不熟悉怎么将文件上传 Gitee:我…...
——Socket套接字)
网络编程套接字(2)——Socket套接字
目录 一、概念 二、分类 1、流套接字(使用传输层TCP协议) TCP的特点 2、数据报套接字(使用传输层UDP协议) UDP的特点 3、原始套接字 一、概念 Socket套接字,是由系统提供用于网络通信的技术,是基于T…...
向量错题本
《1800》 1 看变换求和能不能成为0,为0,就是线性相关 2 矩阵等价 3 4<...
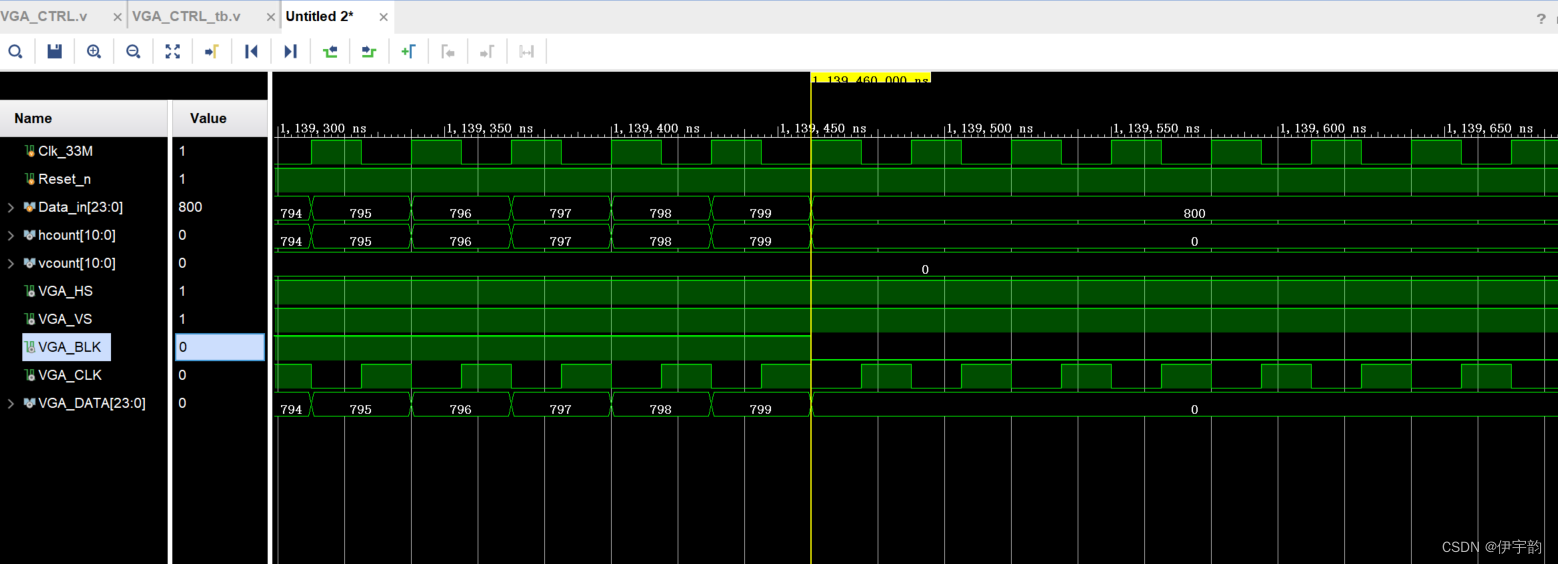
FPGA-VGA成像原理与时序
什么是VGA: VGA, Video Graphics Array。即视频图形阵列,具有分辨率高、显示速率快、颜色丰富等优点。VGA接口不但是CRT显示设备的标准接口,同样也是LCD液晶显示设备的标准接口,具有广泛的应用范围。在FGPA中,常广泛用于图像处理等领域。 VGA 显示器成像原理 在 VGA 标准刚兴…...

【VTKExamples::Points】第三期 ExtractClusters
很高兴在雪易的CSDN遇见你 VTK技术爱好者 QQ:870202403 公众号:VTK忠粉 前言 本文分享VTK样例ExtractClusters,并解析接口vtkEuclideanClusterExtraction,希望对各位小伙伴有所帮助! 感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步! 你的点赞就是我…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
