【算法训练营】最长公共子序列,倒水问题,奶牛吃草(Python实现)
最长公共子序列
时间限制:1 sec
空间限制:256 MB
问题描述
给定两个 1 到 n 的排列 A,B (即长度为 n 的序列,其中 [1,n] 之间的所有数都出现了恰好一次)。
求它们的最长公共子序列长度。
输入格式
第一行一个整数 n ,意义见题目描述。
第二行 n 个用空格隔开的正整数 A[1],…,A[n],描述排列 A。
第三行 n 个用空格隔开的正整数 B[1],…,B[n],描述排列 B。
输出格式
一行一个整数,表示 A,B 的最长公共子序列的长度。
样例输入
5
1 2 4 3 5
5 2 3 4 1
样例输出
2
样例解释
(2,3) 和 (2,4) 都可以是这两个序列的最长公共子序列。
数据范围
对于 80% 的数据,保证 n<=5,000。
对于 100% 的数据,保证 n<=50,000。
提示
[把 A 中的所有数替换成其在 B 中出现的位置,想一想,新序列的最长上升子序列和所求的东西有什么关系呢?]
代码实现
def cal_loc():for i in range(1, n + 1):loc[b[i]] = idef lis():a[1] = b[1]k = 1for i in range(2, n + 1):if a[k] < b[i]:k += 1a[k] = b[i]else:l, r = 1, kwhile l <= r:mid = (l + r) // 2if a[mid] < b[i]:l = mid + 1else:r = mid - 1a[l] = b[i]return kn = int(input())
a = [0] + list(map(int, input().split()))
b = [0] + list(map(int, input().split()))
loc = [0] * (n + 1)cal_loc()for i in range(1, n + 1):b[i] = loc[a[i]]print(lis())倒水问题
时间限制:10 sec
空间限制:256 MB
问题描述
邓老师有有 2 个容量分别为 n 单位、m 单位的没有刻度的杯子。初始,它们都是空的。
邓老师给了你 t 分钟时间。每一分钟,他都可以做下面 4 件事中的任意一件:
- 用水龙头装满一个杯子。
- 倒空一个杯子。
- 把一个杯子里的水倒到另一个杯子里,直到一个杯子空了或者另一个杯子满了。
- 什么都不做。
邓老师希望最后能获得 d 个单位的水,假设最后两个杯具中水量的总和为 x,那么邓老师的不满意度就为 |d-x|。
你希望邓老师尽可能地满意,于是请你计算邓老师的不满意度最小是多少。
输入格式
一行 4 个整数 n,m,t,d,分别表示两个杯具的容量、时间限制、以及邓老师的期望值。
输出格式
一行一个整数,表示邓老师最小的不满意度。
样例输入
7 25 2 16
样例输出
9
样例解释
你可以在第 1 分钟用水龙头装满任意一个杯子,并在第 2 分钟什么都不做,即可让邓老师的不满意度为 9。
可以证明不存在更优的解。
数据范围
本题共设置 16 个测试点。
对于前 1 个测试点,保证 t=1。
对于前 2 个测试点,保证 t<=2。
对于前 4 个测试点,保证 t<=4。
对于前 10 个测试点,保证 1<=n,m<=100,1<=t<=100,1<=d<=200。
对于所有的 16 个测试点,保证 1<=n,m<=2,000,1<=t<=200,1<=d<=4,000。
代码实现
奶牛吃草
时间限制:4 sec
空间限制:256 MB
问题描述
有一只奶牛在一条笔直的道路上(可以看做是一个数轴)。初始,它在道路上坐标为 K 的地方。
这条道路上有 n 棵非常新鲜的青草(编号从 1 开始)。其中第 i 棵青草位于道路上坐标为 x[i] 的地方。贝西每秒钟可以沿着道路的方向向前(坐标加)或向后(坐标减)移动一个坐标单位的距离。
它只要移动到青草所在的地方,就可以一口吞掉青草,它的食速很快,吃草的时间可以不计。
它要吃光所有的青草。不过,青草太新鲜了,在被吞掉之前,暴露在道路上的每棵青草每秒种都会损失一单位的口感。
请你帮它计算,该怎样来回跑动,才能在口感损失之和最小的情况下吃掉所有的青草。
输入格式
第一行两个用空格隔开的整数 n,k,分别表示青草的数目和奶牛的初始坐标。
第 2 行到第 n+1 行,第 i+1 行有一个整数 x[i],描述第 i 棵青草的坐标。
输出格式
一行一个整数,表示吃掉所有青草的前提下,最小损失的口感之和。保证答案在 32 位有符号整数的范围内。
样例输入
4 10
1
9
11
19
样例输出
44
样例解释
先跑到 9,然后跑到 11,再跑到 19,最后到 1,可以让损失的口感总和为 29+1+3+11=44。可以证明不存在比这更优的解。
数据范围
对于 50% 的数据,保证 1≤n≤4,1≤k,x[i]≤20。 对于 80% 的数据,保证 1≤n≤100。 对于 100% 的数据,保证 1≤n≤1000,1≤k,x[i]≤10^6。
提示
[我们先从另一个角度看答案,即损失的总口感:从初始状态到奶牛吃掉第 1 棵草之间的时间(我们在下面把它叫做第 1 段时间),所有的 n 棵青草都在流失口感;……;从奶牛吃掉第 i 棵草到它吃掉第 i+1 棵草之间的时间(我们在下面把它叫做第 i+1 段时间),还没有被吃掉的 n-i 棵草都在流失口感;……]
[于是我们发现,第 i 段时间对答案的贡献,为这段时间的长度与 n-i+1 的乘积。]
[接着,我们再来关注最优策略。吃完一棵草后(包括初始时),奶牛的最优策略一定是直奔另一棵草。]
[由于奶牛不会飞,所以奶牛走过的所有路一定是一段连续的区间。]
[显然地,被奶牛经过过的地方,按最优策略,一定不会留下青草。]
[所以我们可以**将所有青草的坐标排序**(下面我们都使用排完序后的编号),然后用 dp[l][r][j] 表示吃完 [l,r] 范围内的青草时的最小答案,j 只有 0,1 两种取值,分别表示奶牛吃完最后一棵草停在青草 l 还是 r 上(只有可能是这两种情况,否则与上面的结论矛盾)。]
[于是我们就可以轻易地设计出状态转移方程:]
[dp[l][r][0]=min(dp[l+1][r][0]+(n-r+l)*abs(x[l]-x[l+1]),dp[l+1][r][1]+(n-r+l)*abs(x[l]-x[r]))]
[dp[l][r][1]=min(dp[l][r-1][1]+(n-r+l)*abs(x[r]-x[r-1]),dp[l][r-1][0]+(n-r+l)*abs(x[r]-x[l]))]
[边界为:dp[i][i][j]=abs(x[i]-k)*n(对于所有1<=i<=n,j=0,1)]
[友情提示:请注意枚举顺序。]
代码实现
def min_taste_loss(n, k, x):INF = float('inf')dp = [[[INF for _ in range(2)] for _ in range(n + 1)] for _ in range(n + 1)]# Base casefor i in range(1, n + 1):dp[i][i][0] = dp[i][i][1] = abs(x[i] - k) * n# Dynamic programmingfor length in range(2, n + 1):for l in range(1, n - length + 2):r = l + length - 1dp[l][r][0] = min(dp[l + 1][r][0] + (n - r + l) * abs(x[l] - x[l + 1]),dp[l + 1][r][1] + (n - r + l) * abs(x[l] - x[r]))dp[l][r][1] = min(dp[l][r - 1][1] + (n - r + l) * abs(x[r] - x[r - 1]),dp[l][r - 1][0] + (n - r + l) * abs(x[r] - x[l]))return min(dp[1][n][0], dp[1][n][1])# 读取输入
n, k = map(int, input().split())
x = [0] + [int(input()) for _ in range(n)] # 青草的坐标,下标从1开始# 排序青草的坐标
x.sort()# 输出结果
result = min_taste_loss(n, k, x)
print(result)
相关文章:
)
【算法训练营】最长公共子序列,倒水问题,奶牛吃草(Python实现)
最长公共子序列 时间限制:1 sec 空间限制:256 MB 问题描述 给定两个 1 到 n 的排列 A,B (即长度为 n 的序列,其中 [1,n] 之间的所有数都出现了恰好一次)。 求它们的最长公共子序列长度。 输入格式 第一行一个整数 n &a…...

Armadillo:矩阵类、向量类、Cube类和泛型类
文章目录 矩阵类、向量类、Cube类和泛型类Mat<type>matcx_matCol<type>veccx_vecRow<type>rowveccx_rowvecCube<type>cubecx_cubefield<object_type>SpMat<type>sp_matsp_cx_mat运算符: − * % / ! < > <…...

【守护健康】小脑萎缩患者必备营养指南
当生活给予我们挑战,我们选择用科学和关爱予以回应。面对小脑萎缩这一难题,正确的营养补充不仅是一剂强心针,更是患者康复之路上的坚实伙伴。今天,让我们一起了解那些能够助力小脑萎缩患者的神奇维生素! 1. 维生素B群…...
lvs集群中NAT模式
群集的含义 由多台主机构成,但对外表现为一个整体,只提供一个访问入口,相当于一台大型的计算机。 横向发展:放更多的服务器,有调度分配的问题。 垂直发展:升级单机的硬件设备,提高单个服务器自身功能。 …...
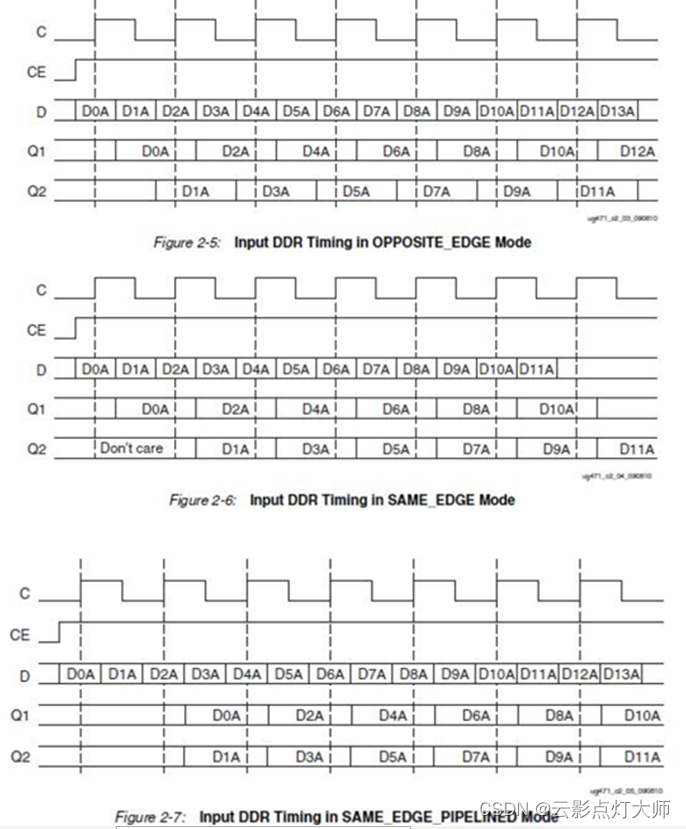
FPGA——三速自适应以太网设计(2)GMII与RGMII接口
FPGA——以太网设计(2)GMII与RGMII 基础知识(1)GMII(2)RGMII(3)IDDR GMII设计转RGMII接口跨时钟传输模块 基础知识 (1)GMII GMII:发送端时钟由MAC端提供 下…...
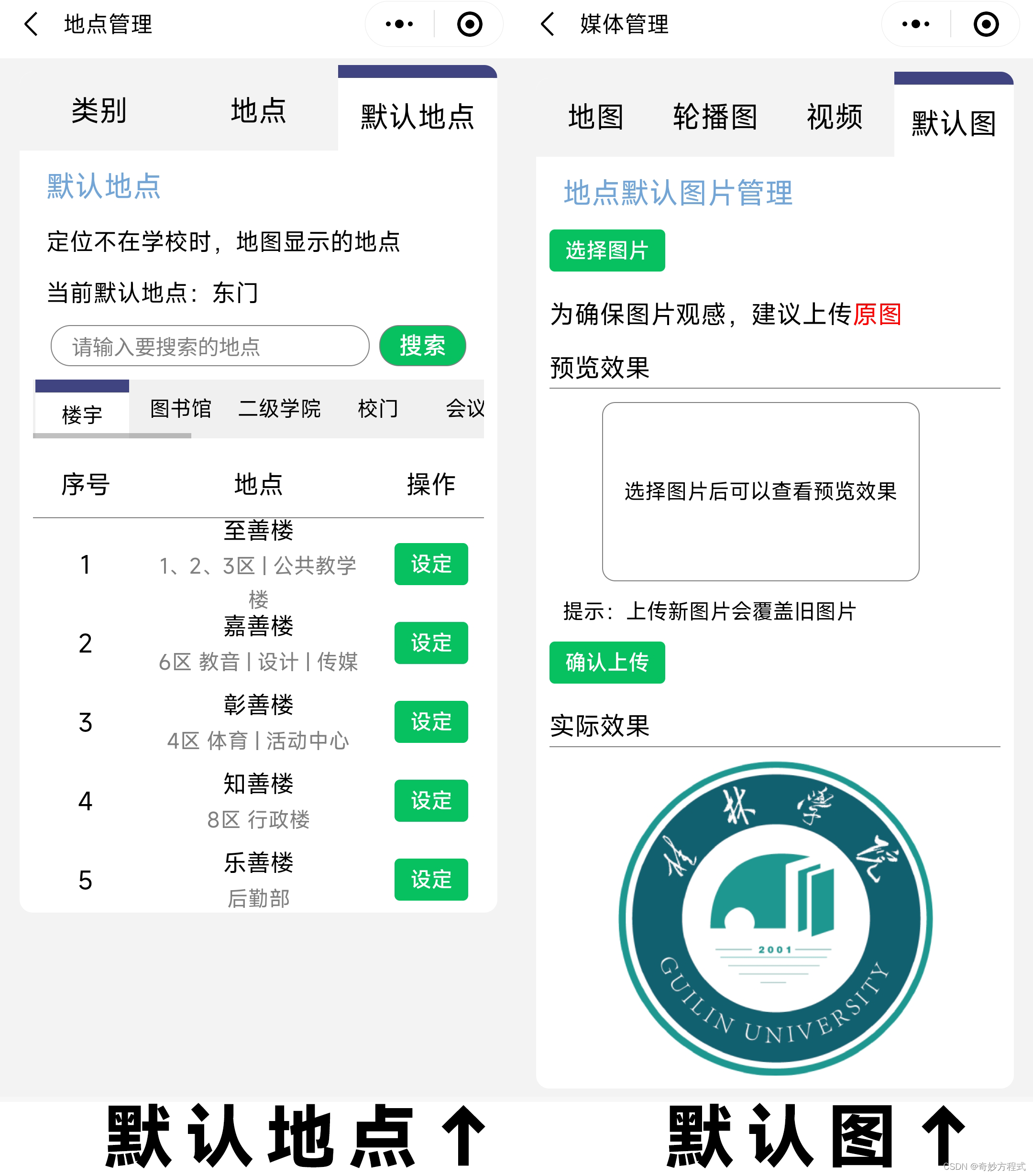
【校园导航小程序】2.0版本 静态/云开发项目 升级日志
演示视频 【校园导航小程序】2.0版本 静态/云开发项目 演示 首页 重做了首页,界面更加高效和美观 校园指南页 新增了 “校园指南” 功能,可以搜索和浏览校园生活指南 地图页 ①弃用路线规划插件,改用SDK开发包。可以无阻通过审核并发布…...
)
深入揭秘Lucene:全面解析其原理与应用场景(二)
本系列文章简介: 本系列文章将深入揭秘Lucene,全面解析其原理与应用场景。我们将从Lucene的基本概念和核心组件开始,逐步介绍Lucene的索引原理、搜索算法以及性能优化策略。通过阅读本文,读者将会对Lucene的工作原理有更深入的了解…...

Java中synchronized关键字、ReentrantLock、volatile关键字是如何实现线程同步的。
在Java中,synchronized关键字、ReentrantLock和volatile关键字这三个是编程中常用于实现线程同步的机制,下面结合代码详细说明一下这三个关键字的用法。 1. synchronized关键字: synchronized关键字是Java语言提供的内置锁机制,…...

路由拦截器
路由拦截可以分为几种不同的类型,每种类型都有其特定的作用和适用场景。以下是常见的几种路由拦截类型及其用途: 身份验证拦截器: 作用: 检查用户是否已经登录或具有有效的身份认证,并根据认证状态决定是否允许用户访问…...

Springboot+vue的物业管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。
演示视频: Springbootvue的物业管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。 项目介绍: 本文设计了一个基于Springbootvue的物业管理系统,采用M(model)Vÿ…...
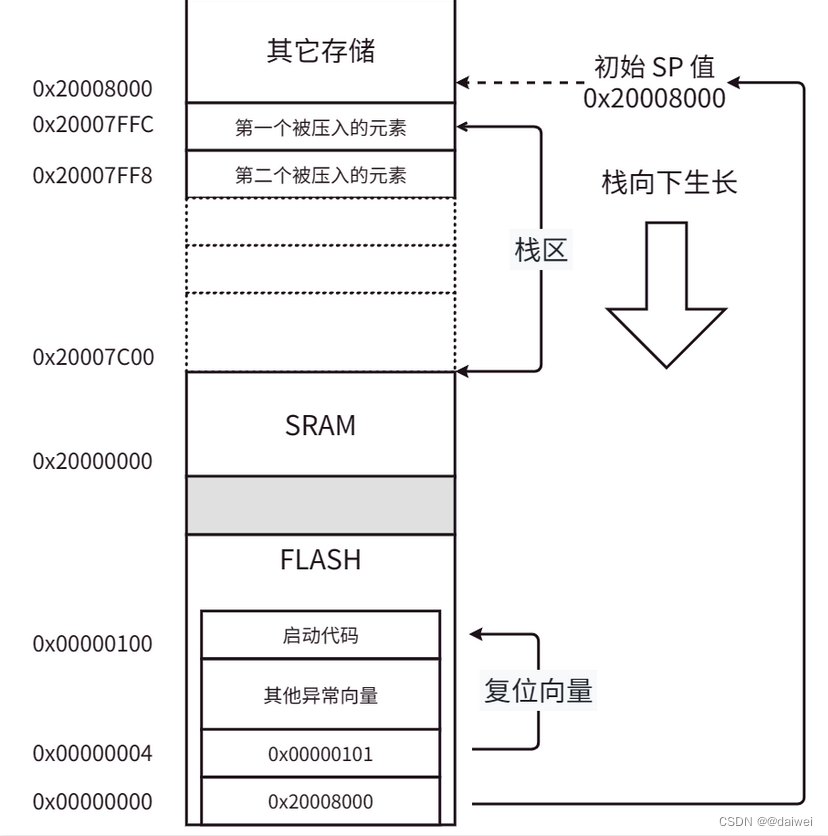
STM32的启动流程分析 和 一些底层控制的原理
阅读引言: 阅读本文之后, 你将对单片机, 甚至是嵌入式系统, 或者是传统的PC机系统的启动流程有一个大致的了解, 本文更加偏向于单片机的启动流程分析。 目录 一、基础知识 1.STM32系列的微控制器(mcu&…...

C#面:几种注释类型
三种常见的注释类型:单行注释、多行注释和 XML 注释。 单行注释: 以双斜线 // 开头,用于在一行中注释单个语句或代码块。单行注释会被编译器忽略,不会对程序的执行产生任何影响。 例如: // 这是一个单行注释 int a…...
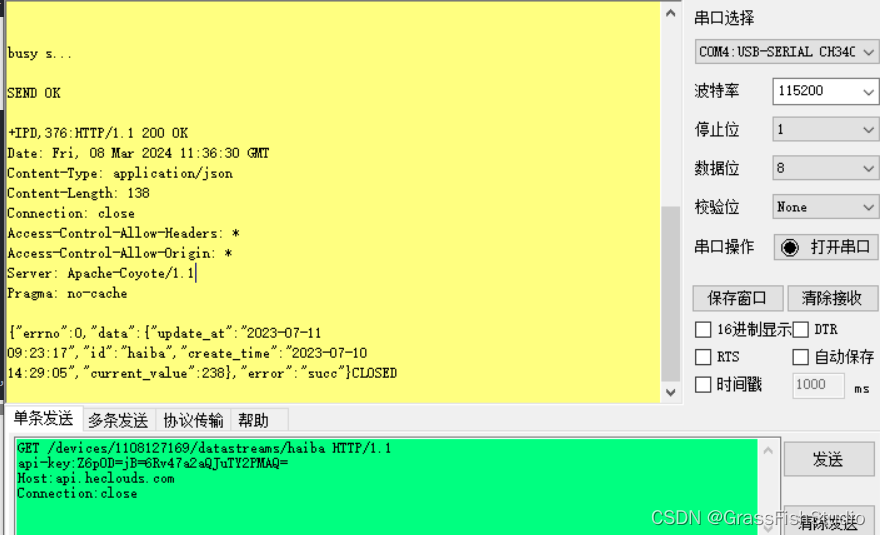
#onenet网络请求http(GET,POST)
参考博文: POST: https://blog.csdn.net/qq_43350239/article/details/104361153 POST请求(用串口助手测试): POST /devices/1105985351/datapoints HTTP/1.1 api-key:AdbrV5kCRsKsRCfjboYOCVcF9FY Host:api.heclouds.com Con…...

零基础学习JS--基础篇--索引集合类
数组是由名称和索引引用的值构成的有序列表。 JavaScript 中没有明确的数组数据类型。但是,你可以使用预定义的 Array 对象及其方法来处理应用程序中的数组。Array 对象具有以各种方式操作数组的方法,例如连接、反转和排序。它有一个用于确定数组长度的…...

【硬件工程师面经整理25_AD】
文章目录 1 AD设计电路全流程2 ad和cadence区别-逻辑上的区别 1 AD设计电路全流程 软件AD or 模拟数字? 软件AD:AD设计电路全流程包括以下步骤:选择AD库和添加、画原理图、PCB布局、PCB布线、PCB打样、PCB加工 模拟数字: 需求分…...
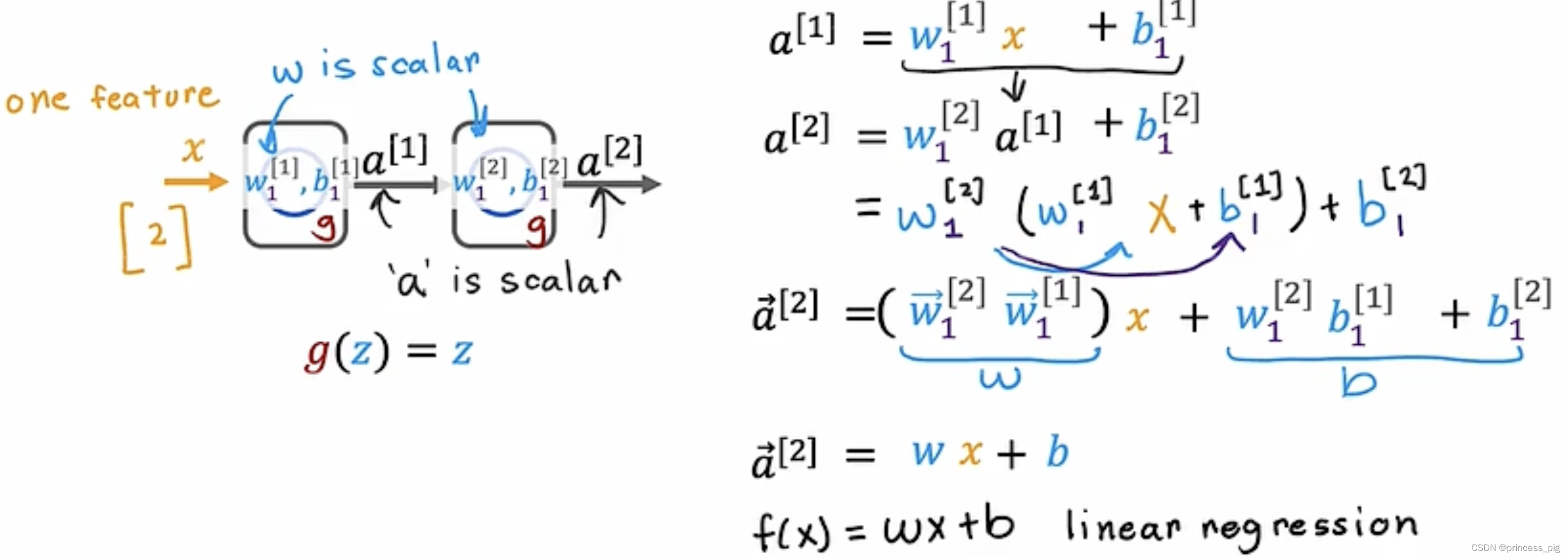
神经网络的矢量化,训练与激活函数
我们现在再回到我们的神经元部分,来看我们如何用python进行正向传递。 单层的正向传递: 我们回到我们的线性回归的函数。我们每个神经元通过上述的方法,就可以得到我们的激发值,从而可以继续进行下一层。 我们用这个方法就可以得…...
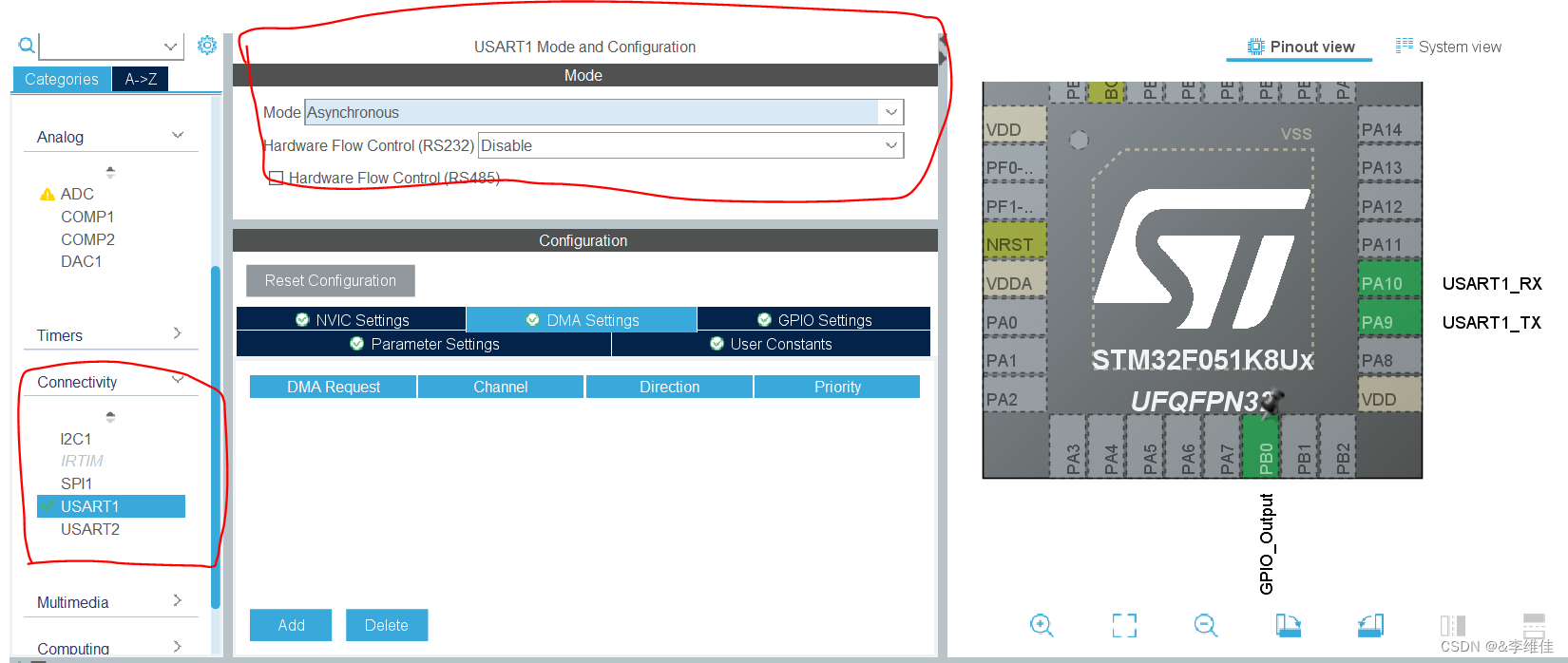
3.7号freeRtoS
1. 串口通信 配置串口为异步通信 设置波特率,数据位,校验位,停止位,数据的方向 同步通信 在同步通信中,数据的传输是在发送端和接收端之间通过一个共享的时钟信号进行同步的。这意味着发送端和接收端的时钟需要保持…...

瑞芯微 | I2S-音频基础 -1
最近调试音频驱动,顺便整理学习了一下i2s、alsa相关知识,整理成了几篇文章,后续会陆续更新。 喜欢嵌入式、Li怒晓得老铁可以关注一口君账号。 1. 音频常用术语 名称含义ADC(Analog to Digit Conversion)模拟信号转换…...
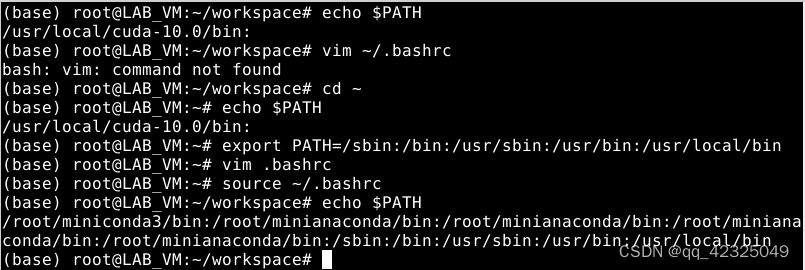
Linux配置.bashrc文件导致各种命令(vim、sudo)失效。
Linux配置.bashrc文件导致各种命令(vim、sudo)失效。 起因是 nvcc-V一直报错:-bash:nvcc: command not found 踩坑记录:上网一查说是没有配置cuda的环境变量。于是去修改了bashrc文件,在最下面…...

Visual Studio 2022 Version 17.9 新功能
Visual Studio 2022 v17.9 为广大 C 开发者引入了一系列好用的新功能和改进优化。 内存布局 现在,你可以使用【内存布局,Memory Layout】功能以可视化的方式来查看对象,结构体及联合体的内存布局信息,这可比以前需要手动查看内存…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...

codeforces C. Cool Partition
目录 题目简述: 思路: 总代码: https://codeforces.com/contest/2117/problem/C 题目简述: 给定一个整数数组,现要求你对数组进行分割,但需满足条件:前一个子数组中的值必须在后一个子数组中…...
