代码随想录阅读笔记-哈希表【四数之和】
题目
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:答案中不可以包含重复的四元组。
示例:
给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
满足要求的四元组集合为: [ [-1, 0, 0, 1], [-2, -1, 1, 2], [-2, 0, 0, 2] ]
思路
四数之和,和代码随想录阅读笔记-哈希表【三数之和】-CSDN博客是一个思路,都是使用双指针法, 基本解法就是在代码随想录阅读笔记-哈希表【三数之和】-CSDN博客的基础上再套一层for循环。但是有一些细节需要注意,例如: 不要判断nums[k] > target 就返回了,三数之和 可以通过 nums[i] > 0 就返回了,因为 0 已经是确定的数了,四数之和这道题目 target是任意值。比如:数组是[-4, -3, -2, -1],target是-10,不能因为-4 > -10而跳过。但是我们依旧可以去做剪枝,逻辑变成nums[i] > target && (nums[i] >=0 || target >= 0)就可以了。
代码随想录阅读笔记-哈希表【三数之和】-CSDN博客的双指针解法是一层for循环num[i]为确定值,然后循环内有left和right下标作为双指针,找到nums[i] + nums[left] + nums[right] == 0。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下标作为双指针,找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是O(n^2),四数之和的时间复杂度是O(n^3) 。那么一样的道理,五数之和、六数之和等等都采用这种解法。
对于代码随想录阅读笔记-哈希表【三数之和】-CSDN博客双指针法就是将原本暴力O(n^3)的解法,降为O(n^2)的解法,四数之和的双指针解法就是将原本暴力O(n^4)的解法,降为O(n^3)的解法。
之前博客的经典题目:代码随想录阅读笔记-哈希表【四数相加II】-CSDN博客,相对于本题简单很多,因为本题是要求在一个集合中找出四个数相加等于target,同时四元组不能重复。而代码随想录阅读笔记-哈希表【四数相加II】-CSDN博客是四个独立的数组,只要找到A[i] + B[j] + C[k] + D[l] = 0就可以,不用考虑有重复的四个元素相加等于0的情况,所以相对于本题还是简单了不少。
我们来回顾一下,几道题目使用了双指针法。
双指针法将时间复杂度:O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级,除了本题还有之前写过的题目如下:
- 代码随想录阅读笔记-数组【移除元素】-CSDN博客
- 代码随想录阅读笔记-哈希表【三数之和】-CSDN博客
链表相关双指针题目:
- 代码随想录阅读笔记-链表【反转链表】-CSDN博客
- 代码随想录阅读笔记-链表【删除链表倒数第n节点】-CSDN博客
- 代码随想录阅读笔记-链表【链表相交】-CSDN博客
- 代码随想录阅读笔记-链表【环形链表II】-CSDN博客
双指针法在字符串题目中还有很多应用,后面还会介绍到。
C++代码:
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> result;sort(nums.begin(), nums.end());for (int k = 0; k < nums.size(); k++) {// 剪枝处理if (nums[k] > target && nums[k] >= 0) {break; // 这里使用break,统一通过最后的return返回}// 对nums[k]去重if (k > 0 && nums[k] == nums[k - 1]) {continue;}for (int i = k + 1; i < nums.size(); i++) {// 2级剪枝处理if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) {break;}// 对nums[i]去重if (i > k + 1 && nums[i] == nums[i - 1]) {continue;}int left = i + 1;int right = nums.size() - 1;while (right > left) {// nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出if ((long) nums[k] + nums[i] + nums[left] + nums[right] > target) {right--;// nums[k] + nums[i] + nums[left] + nums[right] < target 会溢出} else if ((long) nums[k] + nums[i] + nums[left] + nums[right] < target) {left++;} else {result.push_back(vector<int>{nums[k], nums[i], nums[left], nums[right]});// 对nums[left]和nums[right]去重while (right > left && nums[right] == nums[right - 1]) right--;while (right > left && nums[left] == nums[left + 1]) left++;// 找到答案时,双指针同时收缩right--;left++;}}}}return result;}
};
- 时间复杂度: O(n^3)
- 空间复杂度: O(1)
优化二级剪枝的部分:
if (nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) {break;
}
可以优化为:
if (nums[k] + nums[i] > target && nums[i] >= 0) {break;
}
因为只要 nums[k] + nums[i] > target,那么想要符合题意的唯一条件就是此时nums[k] 和 nums[i]都为负数,所以需要nums[i]后面还有负数,才能使和变小进而去接近target,那么 nums[i] 后面的数都是正数的话,就一定 不符合条件了。
相关文章:

代码随想录阅读笔记-哈希表【四数之和】
题目 给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a b c d 的值与 target 相等?找出所有满足条件且不重复的四元组。 注意:答案中不可以包…...

JVM学习——双亲委派机制
简而言之就是为了防止与Java固有全类名重复,而导致系统崩坏所设立的机制。 当类加载器接收到加载类的任务时,首先会向上请求,一直请求到引导类加载器,如果引导类加载器无法加载,就会逐层返回让类加载器自己执行&#…...
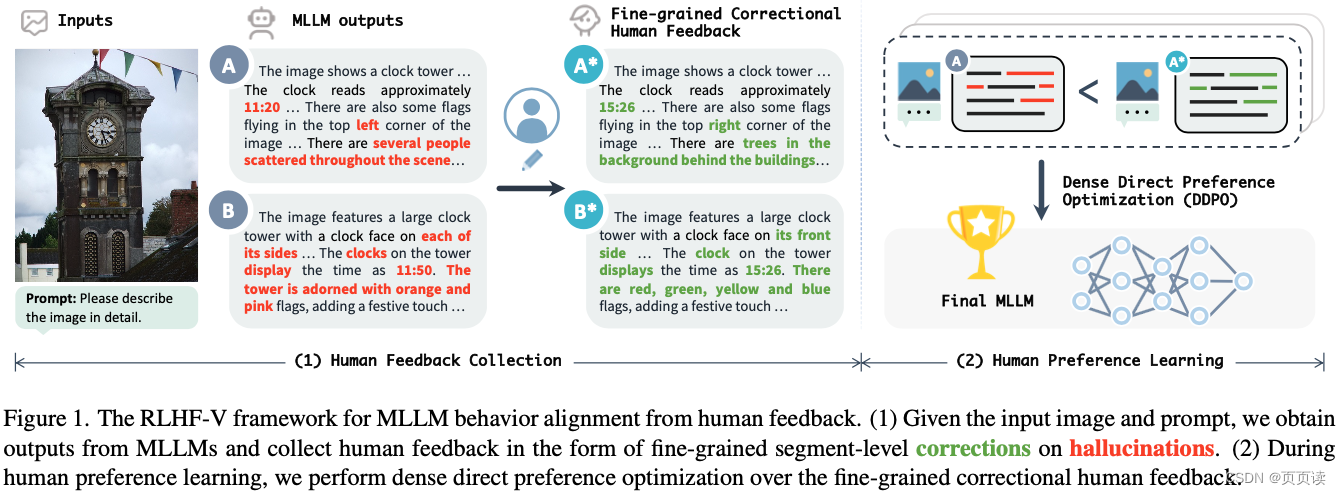
【Paper Reading】6.RLHF-V 提出用RLHF的1.4k的数据微调显著降低MLLM的虚幻问题
分类 内容 论文题目 RLHF-V: Towards Trustworthy MLLMs via Behavior Alignment from Fine-grained Correctional Human Feedback 作者 作者团队:由来自清华大学和新加坡国立大学的研究者组成,包括Tianyu Yu, Yuan Yao, Haoye Zhang, Taiwen He, Y…...

Aloudata 倾力打造,《Data Fabric 白皮书 2.0》正式发布
数字经济时代,越来越多企业开始寻求全新的数据管理范式,以更有效地管理、利用不断增长的数据资产。在此背景下,Data Fabric 的概念应运而生,被视为面向未来的数据管理解决方案。 距离第一版白皮书问世已经过去一年多时间ÿ…...

docker内部无法使用ping等网络工具解决方案
通常docker内部没有网络,所以我们先离线安装需要的依赖包,然后再使用sh脚本容器内部访问宿主机同网络端其他服务器ip,实现监测远程ip telnet包依赖于netbase包,但是netbase包没有安装。你需要先安装netbase包,然后再尝试安装teln…...
后端工程师快速使用vue和Element
文章目录 Vue1 Vue概述2 快速入门3 Vue指令3.1 v-bind和v-model3.2 v-on3.3 v-if和v-show3.4 v-for3.5 案例 4 生命周期 Element快速使用1 Element介绍2 快速入门3 当前页面中嵌套另一个页面案例代码案例截图 Vue 1 Vue概述 通过我们学习的htmlcssjs已经能够开发美观的页面了…...
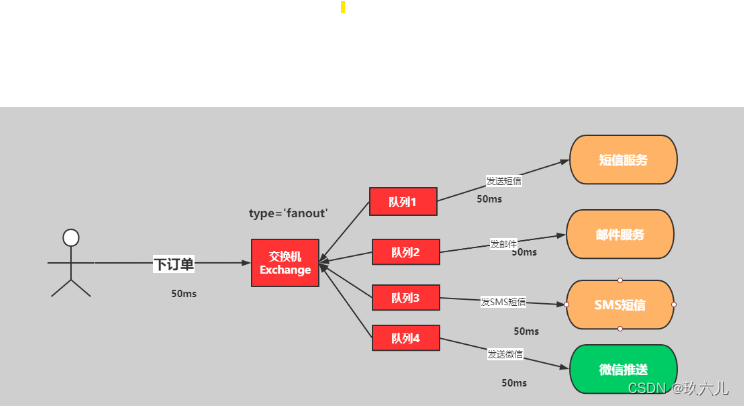
自学rabbitmq入门到精通
交换机的fault (发布与订阅模式) 因为消息是由生产者发送给excahnge,exchange发送给队列, 然后由队列发送给消费者的。 展示使用图形化界面使用fanout模式。 创建交换机 然后创建三个队列,绑定对应的交换机ÿ…...
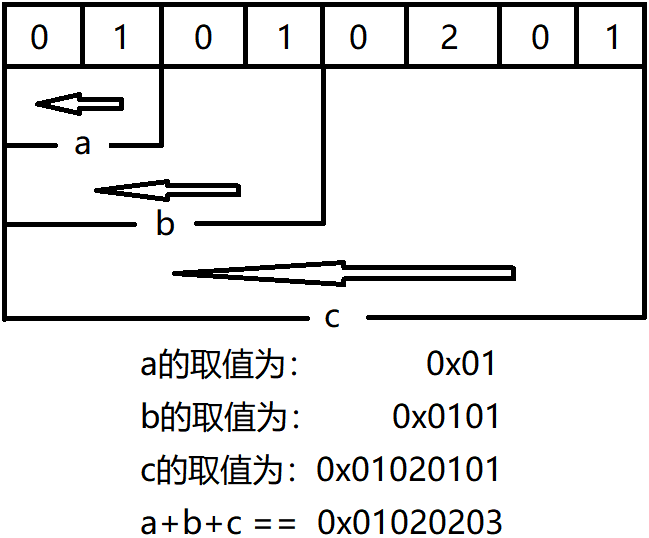
由浅到深认识C语言(13):共用体
该文章Github地址:https://github.com/AntonyCheng/c-notes 在此介绍一下作者开源的SpringBoot项目初始化模板(Github仓库地址:https://github.com/AntonyCheng/spring-boot-init-template & CSDN文章地址:https://blog.csdn…...
python爬虫(9)之requests模块
1、获取动态加载的数据 1、在开发者工具中查看动态数据 找到csdn的门户的开发者工具后到这一页面。 2、加载代码 import requests headers {User-Agent:Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/122.0.0.0 Safari/537.36…...

phpstudy自定义安装mysql8.3并启动
phpstudy自定义安装mysql8.3并启动 先去官网:https://dev.mysql.com/downloads/下载压缩包文件 然后按下面的图片一步一步操作 选择版本,选择第一个压缩包文件,下载 下载完成后,解压到phpstudy环境目录下,如下图 然后进入mysq…...

Netty 学习资料
Netty 学习资料 搜集了一下Java网络库Netty的学习资料,整理如下,有空花时间研究一下。 1、Netty学习手册 《尚硅谷 Netty 核心技术及源码剖析》课程学习手册 本课程不适合零基础的学员,需要掌握常用的设计模式和数据结构 掌握 Java 的面向对…...

【概率论中的两种重要公式:全概率和贝叶斯】
贝叶斯公式(Bayes’ Theorem)是概率论中的一条重要定理,用于计算条件概率。它描述了在已知某一事件发生的条件下,另一事件发生的概率。贝叶斯公式如下所示: P ( A ∣ B ) P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) \…...

python中的闭包
一、闭包 1、作用域 在Python代码中,作用域分为两种情况:全局作用域 与 局部作用域 2、变量的作用域 在全局定义的变量 > 全局变量 在局部定义的变量 > 局部变量 3、全局变量与局部变量的访问范围 ① 在全局作用域中可以访问全局变量&#…...

成功解决RuntimeError: OpenSSL 3.0‘s legacy provider failed to load
报错 RuntimeError: OpenSSL 3.0s legacy provider failed to load. This is a fatal error by default, but cryptography supports running without legacy algorithms by setting the environment variable CRYPTOGRAPHY_OPENSSL_NO_LEGACY. If you did not expect this er…...

【 React 】React 组件之间如何通信?
相关文章: React Context的使用方法 react Provider Consumer 使用方法 1. 是什么 我们将组件间通信可以拆分为两个词: 组件通信 组件是vue中最强大的功能之一,同样组件化是React的核心思想 相比vue,React的组件更加灵活和多样…...
汇总全网免费API,持续更新(新闻api、每日一言api、音乐。。。)
Public&FreeAPI 网址:apis.whyta.cn (推荐) UomgAPI 网址:https://api.uomg.com 教书先生 网址:https://api.oioweb.cn/ 山海API https://api.shserve.cn/ 云析API铺 https://api.a20safe.com/ 韩小韩…...

Android SystemServer进程解析
SystemServer进程在android系统中占了举足轻重的地位,系统的所有服务和SystemUI都是由它启动。 一、SystemServer进程主函数流程 1、主函数三部曲 //frameworks/base/services/java/com/android/server/SystemServer.java /** * The main entry point from zy…...

Github主页设置贪吃蛇详细教程
先看最终实现结果: 有条贪吃蛇放在主页还是蛮酷的哈哈哈。接下来我来讲一讲怎么在Github主页添加一条贪吃蛇。 首先要修改自己的Github的主页,我们得有一个特殊的仓库——这个仓库必须与你的Github用户名保持一致,并且需要公开,…...

二、实现fastdfs文件上传与延迟删除功能的Spring Boot项目
如何在Spring Boot项目中集成FastDFS实现文件上传功能,并添加支持延迟删除功能的实现。 一、Spring Boot 中集成 fastdfs 使用 1、文件上传功能实现 首先,让我们看一下如何实现文件上传功能的接口方法: RestController public class File…...
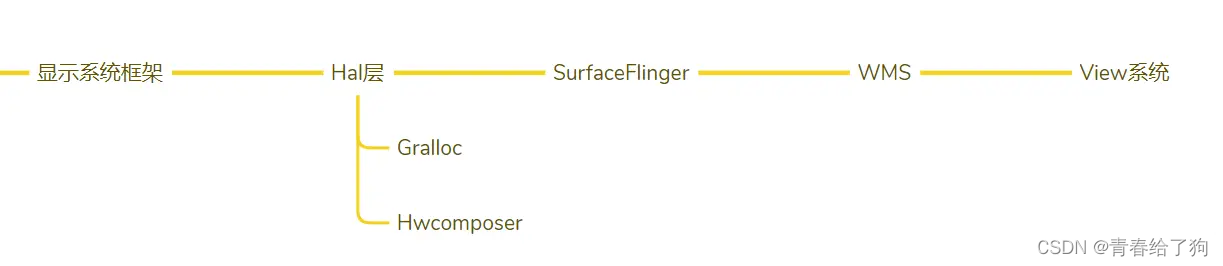
Android FrameWork 学习路线
目录 前言 学习路线: 1.基础知识 2、AOSP 源码学习 3. AOSP 源码编译系统 4. Hal与硬件服务 5.基础组件 6. Binder 7. 系统启动过程分析 8. 应用层框架编辑 9. 显示系统 10. Android 输入系统 11. 系统应用 前言 Android Framework 涉及的行业相当广…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
