过路费的题解
目录
原题描述:
题目描述
输入格式:
输出格式:
样例输入:
样例输出:
数据范围:
提示:
主要思路:
code:
原题描述:
题目描述
在某个遥远的国家里,有n个城市。编号为1,2,3,…,n。这个国家的政府修建了m条双向道路,每条道路连接着两个城市。政府规定从城市S到城市T需要收取的过路费为所经过城市之间道路长度的最大值。如:A到B长度为2,B到C长度为3,那么开车从A经过B到C需要上交的过路费为3。
佳佳是个做生意的人,需要经常开车从任意一个城市到另外一个城市,因此他需要频繁地上交过路费,由于忙于做生意,所以他无时间来寻找交过路费最低的行驶路线。然而,当他交的过路费越多他的心情就变得越糟糕。作为秘书的你,需要每次根据老板的起止城市,提供给他从开始城市到达目的城市,最少需要上交多少过路费。
输入格式:
第一行是两个整数n 和m,分别表示城市的个数以及道路的条数。
接下来m行,每行包含三个整数 a,b,w(1≤a,b≤n,0≤w≤10^9),表示a与b之间有一条长度为w的道路。
接着有一行为一个整数q,表示佳佳发出的询问个数。
再接下来q行,每一行包含两个整数S,T(1≤S,T≤n,S≠T), 表示开始城市S和目的城市T。
输出格式:
输出文件共q行,每行一个整数,分别表示每个询问需要上交的最少过路费用。输入数据保证所有的城市都是连通的。
样例输入:
4 5
1 2 10
1 3 20
1 4 100
2 4 30
3 4 10
2
1 4
4 1样例输出:
20
20数据范围:
对于30%的数据,满足1≤ n≤1000,1≤m≤10000,1≤q≤100;
对于50%的数据,满足1≤ n≤10000,1≤m≤10000,1≤q≤10000;
对于100%的数据,满足1≤ n≤10000,1≤m≤100000,1≤q≤10000;
提示:
remove!!!
主要思路:
这题是树上求最大值,我们可以证明,最小代价路径一定在最小生成树上,所以要用Kruskal和并查集。
接着,有树,就会有LCA,我们在树上求个最大值,famax[i][j]是从i向上跳所到达的点。
famax的初始化和fa的初始化差不多。
那具体LCA怎么求,不会请自行上网查找。
只要在LCA里加一个取max就可以了。
code:
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<vector<pair<int,int>>> v(400010);
int depth[400010];
int fa[400010][40];
int fath[400010];
int famax[400010][40];
struct edgenode{int x,y,w;bool operator < (const edgenode& W)const{return w<W.w;}
}a[400010];
int find(int x)
{if(fath[x] == x){return x;}return fath[x] = find(fath[x]);
}
void Kruskal()
{sort(a+1,a+1+m);for(int i=1;i<=m;i++){int x=find(a[i].x),y=find(a[i].y);if(x!=y){fath[x] = y;v[x].push_back({y,a[i].w});v[y].push_back({x,a[i].w});}}
}
void dfs(int x,int fat)
{fa[x][0] = fat;for(int i=0;fa[x][i];++i){fa[x][i+1] = fa[fa[x][i]][i];famax[x][i+1] = max(famax[x][i],famax[fa[x][i]][i]);}for(auto it:v[x]){if(it.first!=fat){depth[it.first] = depth[x]+1;famax[it.first][0] = it.second;dfs(it.first,x);}}
}
int LCA(int x,int y)
{int ans=0;if(depth[x]<depth[y]){swap(x,y);}for(int i=20;i>=0;--i){int d=depth[x]-depth[y];if((1<<i)&d){ans = max(famax[x][i],ans);x = fa[x][i];}}if(x == y){return ans;}for(int i=__lg(depth[x]);i>=0;--i){ if(fa[x][i]!=fa[y][i]){ans = max({ans,famax[x][i],famax[y][i]});x = fa[x][i];y = fa[y][i];}}ans = max({ans,famax[x][0],famax[y][0]});return ans;
}
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cin>>n>>m;for(int i=1;i<=m;i++){cin>>a[i].x>>a[i].y>>a[i].w;}for(int i=1;i<=n;i++){fath[i] = i;}Kruskal();dfs(1,0);int q;cin>>q;while(q--){int s,t;cin>>s>>t;cout<<LCA(s,t)<<'\n';}return 0;
}相关文章:
过路费的题解
目录 原题描述: 题目描述 输入格式: 输出格式: 样例输入: 样例输出: 数据范围: 提示: 主要思路: code: 原题描述: 题目描述 在某个遥远的国家里,有…...

51单片机LED8*8点阵显示坤坤跳舞打篮球画面
我们作为一名合格的 ikun,专业的小黑子,这个重要的知识必须学会。 先看效果: 51LED点阵_鸡你太美 这里我们首先要用到延时函数Delay: void Delay(unsigned int xms) {unsigned char i, j;while(xms--){ i 2;j 239;do{while (-…...

C++_day6:2024/3/18
作业1:编程题: 以下是一个简单的比喻,将多态概念与生活中的实际情况相联系: 比喻:动物园的讲解员和动物表演 想象一下你去了一家动物园,看到了许多不同种类的动物,如狮子、大象、猴子等。现在…...

汇编语言和IBM的关系
一 缺乏汇编的硬件没有灵魂 1964年,在IBM没有发明System 360大型计算机之前,IBM已经发明了很多计算机。如IBM 1952年发布的第一台商用计算机:701计算机。1959年,IBM首次利用晶体管、磁芯存储器、印刷电路技术,发明了小…...

堆(数据结构)
堆的概念及结构 如果有一个关键码的集合K { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: < 且 < ( > 且 > ) i 0,1ÿ…...

医药工厂5G智能制造数字孪生可视化平台,推进医药企业数字化转型
医药工厂5G智能制造数字孪生可视化平台,推进医药企业数字化转型。随着科技的不断发展,数字化转型已成为医药企业不可或缺的一部分。5G智能制造医药工厂数字孪生可视化平台作为数字化转型的重要工具,正在逐步改变医药企业的生产方式和管理模式…...
C语言学习--八种排序算法
目录 排序的概念 1.直接插入排序 基本思想 代码实现 算法分析 2.希尔排序 基本思想 代码实现 算法分析 3.冒泡排序 基本思想 代码实现 算法分析 4.快速排序 基本思想 代码实现 算法分析 5.简单选择排序 基本思想 代码实现 算法分析 6.堆排序 基本思想 代…...
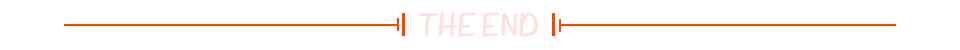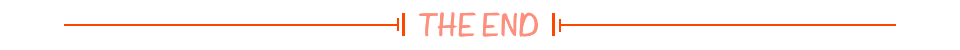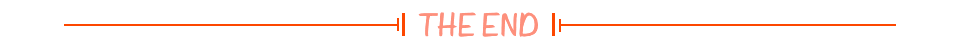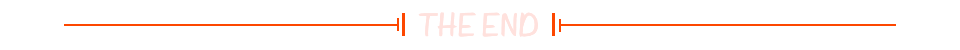
Infineon_TC264智能车代码初探及C语言深度学习(二)
本篇文章记录我在智能车竞赛中,对 Infineon_TC264 这款芯片的底层库函数的学习分析。通过深入地对其库函数进行分析,C语言深入的知识得以再次在编程中呈现和运用。故觉得很有必要在此进行记录分享一下。 目录 编辑 一、代码段分析 NO.1 指向结构体…...

第十三届蓝桥杯(C/C++ 大学B组)
目录 试题 A: 九进制转十进制 试题 B: 顺子日期 试题 C: 刷题统计 试题 D: 修剪灌木 试题 E: X 进制减法 试题 F: 统计子矩阵 试题 G: 积木画 试题 H: 扫雷 试题 I: 李白打酒加强版 试题 J: 砍竹子 试题 A: 九进制转十进制 九进制正整数 ( 2022 )转换成十进制等于多…...
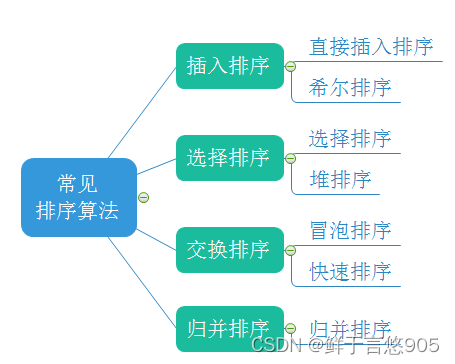
数据结构从入门到精通——排序的概念及运用
排序的概念及运用 前言一、排序的概念排序稳定性内部排序外部排序 二、排序运用三、常见的排序算法四、排序性能检测代码srand()clock() 五、oj排序测试代码 前言 排序是将数据按照一定规则重新排列的过程,常见规则有升序、降序等。排序算法如冒泡排序、快速排序等…...
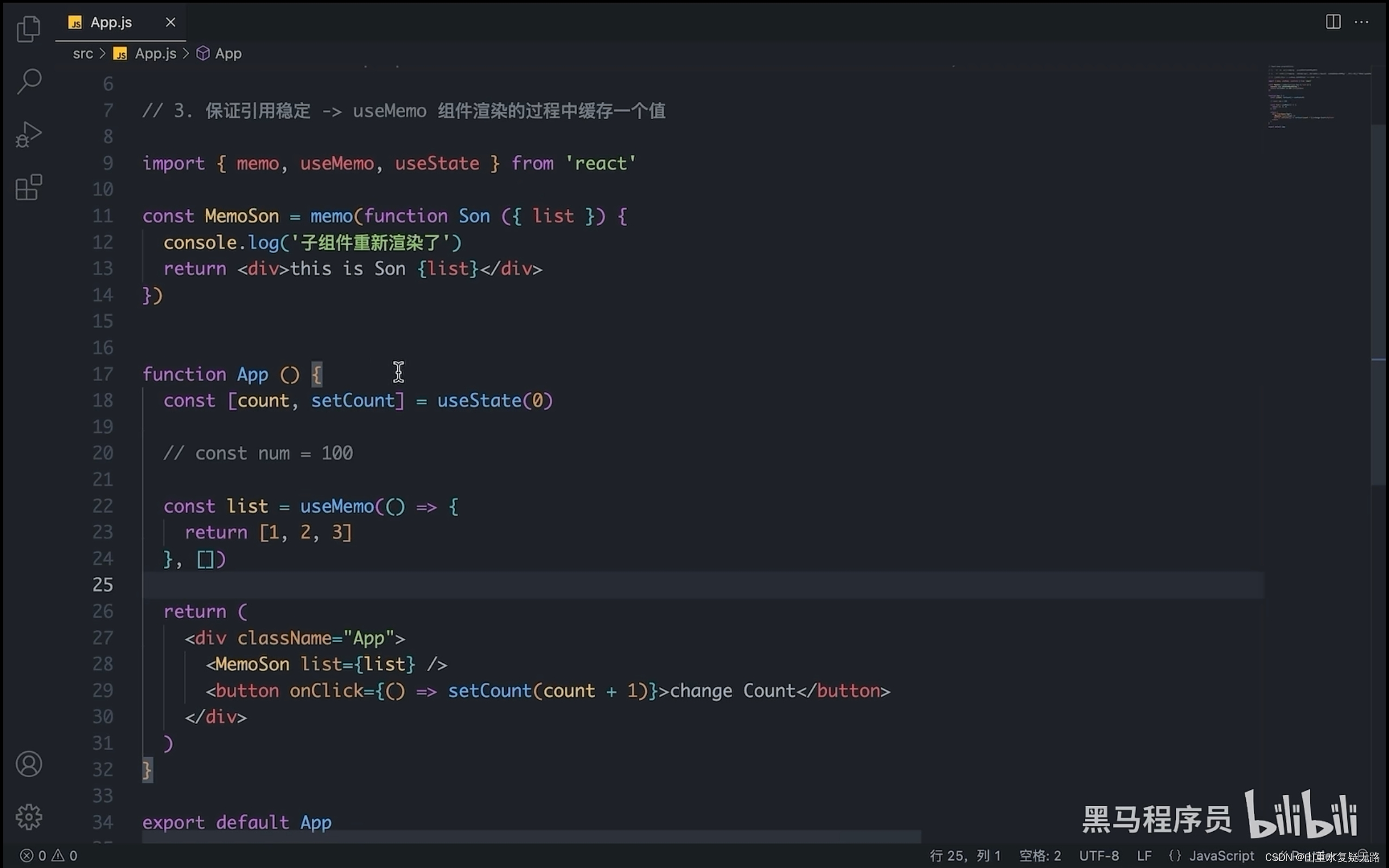
react面试题总结
1、当调用 setState的时候,发生了什么操作? 当调用 setState时, React做的第一件事是将传递给setState的对象合并到组件的当前状态,这将启动一个称为和解( reconciliation)的过程。 和解的最终目标是&#…...
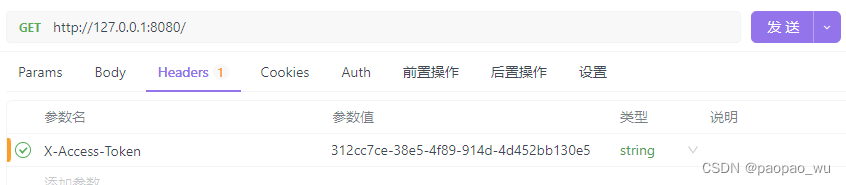
5_springboot_shiro_jwt_多端认证鉴权_禁用Cookie
1. Cookie是什么 Cookie是一种在客户端(通常是用户的Web浏览器)和服务器之间进行状态管理的技术。当用户访问Web服务器时,服务器可以向用户的浏览器发送一个名为Cookie的小数据块。浏览器会将这个Cookie存储在客户端,为这个Co…...

条形码申请指南:外地人如何成功注册香港条形码
香港条形码是打造的通行证,消费者对香港条码有一定的认知,拥有香港条形码就获得消费者对产品的认可,香港条形码是全球条码中具有防伪功能的条形码,化妆品、护肤品、保健品、包装食品等行业的产品认证,就有必要申请香港…...

Covalent Network借助大规模的历史Web3数据集,推动人工智能发展
人工智能在众多领域中增强了区块链的实用性,反之亦然,区块链确保了 AI 模型所使用的数据的来源和质量。人工智能带来的生产力提升,将与区块链系统固有的安全性和透明度融合。 Covalent Network(CQT)正位于这两项互补技…...

test测试类-变量学习
test测试类 作用:标记到类上成为测试类,标记到方法上成为测试方法 变量:测试类的变量,在测试类括号中应用 1、invocationCount变量 意思是这个方法应该被调用的次数。 在测试框架中,特别是当使用参数化测试或数据驱动…...

【DL经典回顾】激活函数大汇总(二十七)(Bent Identity附代码和详细公式)
激活函数大汇总(二十七)(Bent Identity附代码和详细公式) 更多激活函数见激活函数大汇总列表 一、引言 欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不可或…...

element-plus el-table表格默认选中某一行
需求:进入页面时默认选中表格第一行 <el-tableref"singleTableRef":data"tableData"highlight-current-rowrow-click"handleCurrentChange" ><el-table-column property"date" label"日期" /><…...

Vue+SpringBoot打造民宿预定管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用例设计2.2 功能设计2.2.1 租客角色2.2.2 房主角色2.2.3 系统管理员角色 三、系统展示四、核心代码4.1 查询民宿4.2 新增民宿4.3 新增民宿评价4.4 查询留言4.5 新增民宿订单 五、免责说明 一、摘要 1.1 项目介绍 基于…...
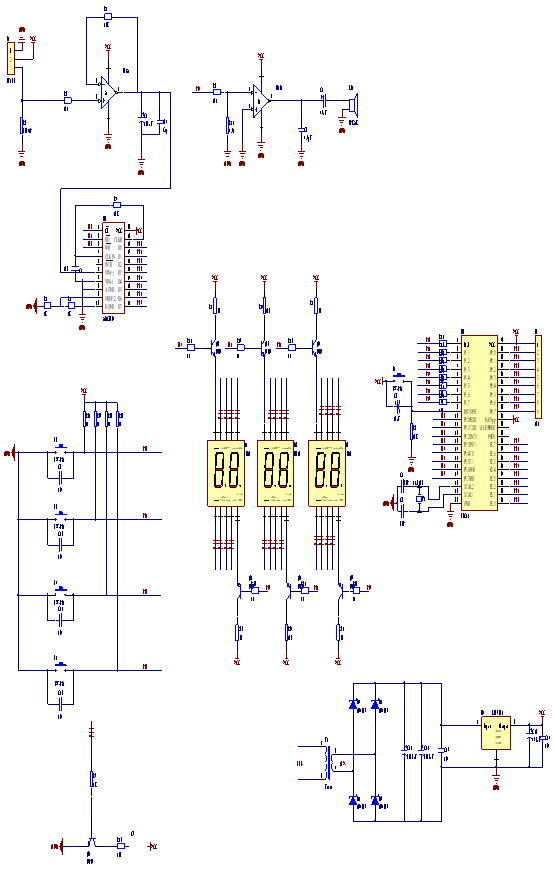
基于单片机的模糊PID炉温控制系统设计
摘 要 电热炉是在工业热处理的生产中广泛使用的一种设备,电热炉的温度控制系统存在时变性,非线性,滞后性等特征,难以用常规PID的控制器对系统达到很好的控制效果。当控温精度的要求高时,使用传统的控制理论方法难以达…...

深入浅出落地应用分析:AI数字人「微软小冰」
hi,各位,今天要聊的是AI小冰,机缘巧合,投递了这家公司的产品,正好最近在看数字人相关的,就详细剖析下这款产品! 前言 小冰,全称为北京红棉小冰科技有限公司,前身为微软(亚洲)互联网工程院人工智能小冰团队,是微软全球最大的人工智能独立产品研发团队。作为微软全…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...
